 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza l'origine su GitHub Visualizza l'origine su GitHub |  Scarica quaderno Scarica quaderno |
Questo tutorial esplora gli algoritmi di calcolo del gradiente per i valori di aspettativa dei circuiti quantistici.
Il calcolo del gradiente del valore atteso di un certo osservabile in un circuito quantistico è un processo coinvolto. I valori di aspettativa delle osservabili non hanno il lusso di avere formule di gradiente analitiche che sono sempre facili da annotare, a differenza delle tradizionali trasformazioni di apprendimento automatico come la moltiplicazione di matrici o l'addizione di vettori che hanno formule di gradiente analitiche facili da annotare. Di conseguenza, esistono diversi metodi di calcolo del gradiente quantistico che risultano utili per diversi scenari. Questo tutorial confronta e mette a confronto due diversi schemi di differenziazione.
Impostare
pip install tensorflow==2.7.0
Installa TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Ora importa TensorFlow e le dipendenze del modulo:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:25:24.733670: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Preliminare
Rendiamo un po' più concreta la nozione di calcolo del gradiente per i circuiti quantistici. Supponiamo di avere un circuito parametrizzato come questo:
qubit = cirq.GridQubit(0, 0)
my_circuit = cirq.Circuit(cirq.Y(qubit)**sympy.Symbol('alpha'))
SVGCircuit(my_circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
Insieme a un osservabile:
pauli_x = cirq.X(qubit)
pauli_x
cirq.X(cirq.GridQubit(0, 0))
Guardando questo operatore sai che \(⟨Y(\alpha)| X | Y(\alpha)⟩ = \sin(\pi \alpha)\)
def my_expectation(op, alpha):
"""Compute ⟨Y(alpha)| `op` | Y(alpha)⟩"""
params = {'alpha': alpha}
sim = cirq.Simulator()
final_state_vector = sim.simulate(my_circuit, params).final_state_vector
return op.expectation_from_state_vector(final_state_vector, {qubit: 0}).real
my_alpha = 0.3
print("Expectation=", my_expectation(pauli_x, my_alpha))
print("Sin Formula=", np.sin(np.pi * my_alpha))
Expectation= 0.80901700258255 Sin Formula= 0.8090169943749475
e se definisci \(f_{1}(\alpha) = ⟨Y(\alpha)| X | Y(\alpha)⟩\) allora \(f_{1}^{'}(\alpha) = \pi \cos(\pi \alpha)\). Controlliamo questo:
def my_grad(obs, alpha, eps=0.01):
grad = 0
f_x = my_expectation(obs, alpha)
f_x_prime = my_expectation(obs, alpha + eps)
return ((f_x_prime - f_x) / eps).real
print('Finite difference:', my_grad(pauli_x, my_alpha))
print('Cosine formula: ', np.pi * np.cos(np.pi * my_alpha))
Finite difference: 1.8063604831695557 Cosine formula: 1.8465818304904567
2. La necessità di un differenziatore
Con circuiti più grandi, non sarai sempre così fortunato ad avere una formula che calcola con precisione i gradienti di un dato circuito quantistico. Nel caso in cui una semplice formula non sia sufficiente per calcolare il gradiente, la classe tfq.differentiators.Differentiator permette di definire algoritmi per calcolare i gradienti dei propri circuiti. Ad esempio, puoi ricreare l'esempio sopra in TensorFlow Quantum (TFQ) con:
expectation_calculation = tfq.layers.Expectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=[[my_alpha]])
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.80901706]], dtype=float32)>
Tuttavia, se si passa alla stima dell'aspettativa basata sul campionamento (cosa accadrebbe su un dispositivo reale), i valori possono cambiare leggermente. Ciò significa che ora hai una stima imperfetta:
sampled_expectation_calculation = tfq.layers.SampledExpectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
sampled_expectation_calculation(my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=[[my_alpha]])
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.836]], dtype=float32)>
Questo può rapidamente trasformarsi in un serio problema di precisione quando si tratta di gradienti:
# Make input_points = [batch_size, 1] array.
input_points = np.linspace(0, 5, 200)[:, np.newaxis].astype(np.float32)
exact_outputs = expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=input_points)
imperfect_outputs = sampled_expectation_calculation(my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=input_points)
plt.title('Forward Pass Values')
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.plot(input_points, exact_outputs, label='Analytic')
plt.plot(input_points, imperfect_outputs, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07d556190>
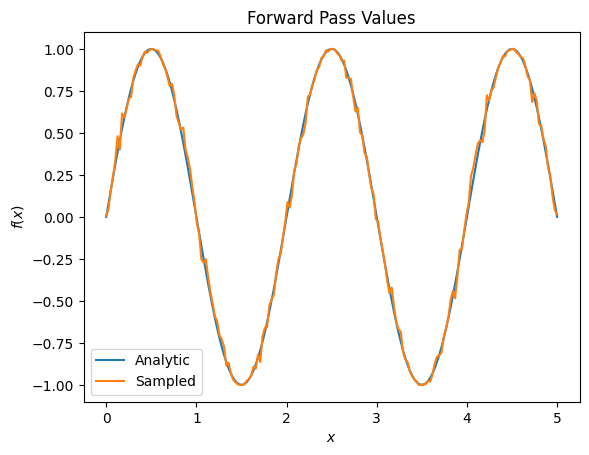
# Gradients are a much different story.
values_tensor = tf.convert_to_tensor(input_points)
with tf.GradientTape() as g:
g.watch(values_tensor)
exact_outputs = expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=values_tensor)
analytic_finite_diff_gradients = g.gradient(exact_outputs, values_tensor)
with tf.GradientTape() as g:
g.watch(values_tensor)
imperfect_outputs = sampled_expectation_calculation(
my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=values_tensor)
sampled_finite_diff_gradients = g.gradient(imperfect_outputs, values_tensor)
plt.title('Gradient Values')
plt.xlabel('$x$')
plt.ylabel('$f^{\'}(x)$')
plt.plot(input_points, analytic_finite_diff_gradients, label='Analytic')
plt.plot(input_points, sampled_finite_diff_gradients, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07adb8dd0>
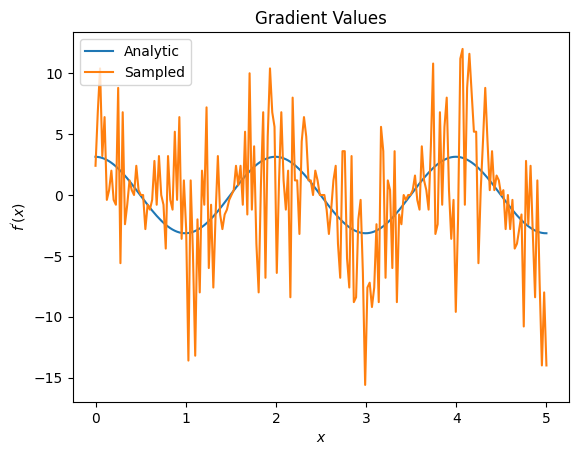
Qui puoi vedere che sebbene la formula alle differenze finite sia veloce per calcolare i gradienti stessi nel caso analitico, quando si trattava di metodi basati sul campionamento era troppo rumoroso. È necessario utilizzare tecniche più attente per garantire che sia possibile calcolare un buon gradiente. Successivamente esaminerai una tecnica molto più lenta che non sarebbe adatta per i calcoli del gradiente di aspettativa analitica, ma si comporta molto meglio nel caso basato su campioni del mondo reale:
# A smarter differentiation scheme.
gradient_safe_sampled_expectation = tfq.layers.SampledExpectation(
differentiator=tfq.differentiators.ParameterShift())
with tf.GradientTape() as g:
g.watch(values_tensor)
imperfect_outputs = gradient_safe_sampled_expectation(
my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=values_tensor)
sampled_param_shift_gradients = g.gradient(imperfect_outputs, values_tensor)
plt.title('Gradient Values')
plt.xlabel('$x$')
plt.ylabel('$f^{\'}(x)$')
plt.plot(input_points, analytic_finite_diff_gradients, label='Analytic')
plt.plot(input_points, sampled_param_shift_gradients, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07ad9ff90>
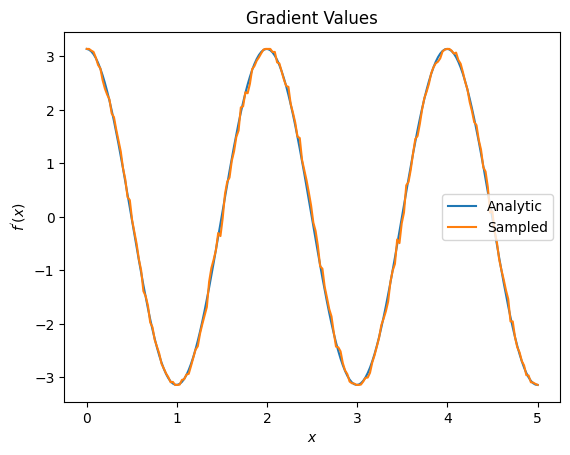
Da quanto sopra puoi vedere che alcuni differenziatori sono utilizzati al meglio per particolari scenari di ricerca. In generale, i metodi basati su campioni più lenti, resistenti al rumore del dispositivo, ecc., sono grandi fattori di differenziazione quando si testano o si implementano algoritmi in un ambiente più "reale". I metodi più veloci come la differenza finita sono ottimi per i calcoli analitici e si desidera una maggiore produttività, ma non sono ancora interessati alla fattibilità del dispositivo del proprio algoritmo.
3. Osservabili multipli
Introduciamo un secondo osservabile e vediamo come TensorFlow Quantum supporta più osservabili per un singolo circuito.
pauli_z = cirq.Z(qubit)
pauli_z
cirq.Z(cirq.GridQubit(0, 0))
Se questo osservabile viene utilizzato con lo stesso circuito di prima, allora hai \(f_{2}(\alpha) = ⟨Y(\alpha)| Z | Y(\alpha)⟩ = \cos(\pi \alpha)\) e \(f_{2}^{'}(\alpha) = -\pi \sin(\pi \alpha)\). Esegui un rapido controllo:
test_value = 0.
print('Finite difference:', my_grad(pauli_z, test_value))
print('Sin formula: ', -np.pi * np.sin(np.pi * test_value))
Finite difference: -0.04934072494506836 Sin formula: -0.0
È una partita (abbastanza vicina).
Ora, se definisci \(g(\alpha) = f_{1}(\alpha) + f_{2}(\alpha)\) allora \(g'(\alpha) = f_{1}^{'}(\alpha) + f^{'}_{2}(\alpha)\). Definire più di un osservabile in TensorFlow Quantum da utilizzare insieme a un circuito equivale ad aggiungere più termini a \(g\).
Ciò significa che il gradiente di un particolare simbolo in un circuito è uguale alla somma dei gradienti rispetto a ciascun osservabile per quel simbolo applicato a quel circuito. Ciò è compatibile con la raccolta e la retropropagazione del gradiente TensorFlow (in cui si fornisce la somma dei gradienti su tutti gli osservabili come gradiente per un particolare simbolo).
sum_of_outputs = tfq.layers.Expectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
sum_of_outputs(my_circuit,
operators=[pauli_x, pauli_z],
symbol_names=['alpha'],
symbol_values=[[test_value]])
<tf.Tensor: shape=(1, 2), dtype=float32, numpy=array([[1.9106855e-15, 1.0000000e+00]], dtype=float32)>
Qui vedi la prima voce è l'aspettativa rispetto a Pauli X, e la seconda è l'aspettativa rispetto a Pauli Z. Ora quando prendi il gradiente:
test_value_tensor = tf.convert_to_tensor([[test_value]])
with tf.GradientTape() as g:
g.watch(test_value_tensor)
outputs = sum_of_outputs(my_circuit,
operators=[pauli_x, pauli_z],
symbol_names=['alpha'],
symbol_values=test_value_tensor)
sum_of_gradients = g.gradient(outputs, test_value_tensor)
print(my_grad(pauli_x, test_value) + my_grad(pauli_z, test_value))
print(sum_of_gradients.numpy())
3.0917350202798843 [[3.0917213]]
Qui hai verificato che la somma dei gradienti per ogni osservabile è effettivamente il gradiente di \(\alpha\). Questo comportamento è supportato da tutti i differenziatori TensorFlow Quantum e gioca un ruolo cruciale nella compatibilità con il resto di TensorFlow.
4. Utilizzo avanzato
Tutti i differenziatori che esistono all'interno della sottoclasse TensorFlow Quantum tfq.differentiators.Differentiator . Per implementare un differenziatore, un utente deve implementare una delle due interfacce. Lo standard prevede l'implementazione di get_gradient_circuits , che indica alla classe base quali circuiti misurare per ottenere una stima del gradiente. In alternativa, puoi sovraccaricare differentiate_analytic e differentiate_sampled ; la classe tfq.differentiators.Adjoint questa strada.
Quanto segue usa TensorFlow Quantum per implementare il gradiente di un circuito. Utilizzerai un piccolo esempio di spostamento dei parametri.
Richiama il circuito che hai definito sopra, \(|\alpha⟩ = Y^{\alpha}|0⟩\). Come prima, puoi definire una funzione come valore atteso di questo circuito rispetto a \(X\) osservabile, \(f(\alpha) = ⟨\alpha|X|\alpha⟩\). Usando le regole di spostamento dei parametri , per questo circuito, puoi scoprire che la derivata è
\[\frac{\partial}{\partial \alpha} f(\alpha) = \frac{\pi}{2} f\left(\alpha + \frac{1}{2}\right) - \frac{ \pi}{2} f\left(\alpha - \frac{1}{2}\right)\]
La funzione get_gradient_circuits restituisce i componenti di questa derivata.
class MyDifferentiator(tfq.differentiators.Differentiator):
"""A Toy differentiator for <Y^alpha | X |Y^alpha>."""
def __init__(self):
pass
def get_gradient_circuits(self, programs, symbol_names, symbol_values):
"""Return circuits to compute gradients for given forward pass circuits.
Every gradient on a quantum computer can be computed via measurements
of transformed quantum circuits. Here, you implement a custom gradient
for a specific circuit. For a real differentiator, you will need to
implement this function in a more general way. See the differentiator
implementations in the TFQ library for examples.
"""
# The two terms in the derivative are the same circuit...
batch_programs = tf.stack([programs, programs], axis=1)
# ... with shifted parameter values.
shift = tf.constant(1/2)
forward = symbol_values + shift
backward = symbol_values - shift
batch_symbol_values = tf.stack([forward, backward], axis=1)
# Weights are the coefficients of the terms in the derivative.
num_program_copies = tf.shape(batch_programs)[0]
batch_weights = tf.tile(tf.constant([[[np.pi/2, -np.pi/2]]]),
[num_program_copies, 1, 1])
# The index map simply says which weights go with which circuits.
batch_mapper = tf.tile(
tf.constant([[[0, 1]]]), [num_program_copies, 1, 1])
return (batch_programs, symbol_names, batch_symbol_values,
batch_weights, batch_mapper)
La classe base Differentiator usa i componenti restituiti da get_gradient_circuits per calcolare la derivata, come nella formula di spostamento dei parametri che hai visto sopra. Questo nuovo differenziatore può ora essere utilizzato con oggetti tfq.layer esistenti:
custom_dif = MyDifferentiator()
custom_grad_expectation = tfq.layers.Expectation(differentiator=custom_dif)
# Now let's get the gradients with finite diff.
with tf.GradientTape() as g:
g.watch(values_tensor)
exact_outputs = expectation_calculation(my_circuit,
operators=[pauli_x],
symbol_names=['alpha'],
symbol_values=values_tensor)
analytic_finite_diff_gradients = g.gradient(exact_outputs, values_tensor)
# Now let's get the gradients with custom diff.
with tf.GradientTape() as g:
g.watch(values_tensor)
my_outputs = custom_grad_expectation(my_circuit,
operators=[pauli_x],
symbol_names=['alpha'],
symbol_values=values_tensor)
my_gradients = g.gradient(my_outputs, values_tensor)
plt.subplot(1, 2, 1)
plt.title('Exact Gradient')
plt.plot(input_points, analytic_finite_diff_gradients.numpy())
plt.xlabel('x')
plt.ylabel('f(x)')
plt.subplot(1, 2, 2)
plt.title('My Gradient')
plt.plot(input_points, my_gradients.numpy())
plt.xlabel('x')
Text(0.5, 0, 'x')
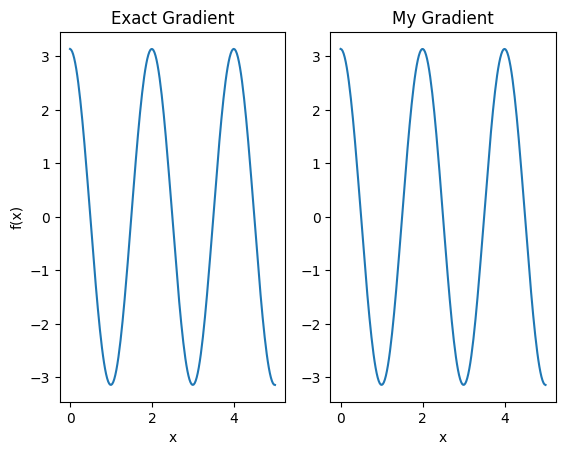
Questo nuovo differenziatore può ora essere utilizzato per generare operazioni differenziabili.
# Create a noisy sample based expectation op.
expectation_sampled = tfq.get_sampled_expectation_op(
cirq.DensityMatrixSimulator(noise=cirq.depolarize(0.01)))
# Make it differentiable with your differentiator:
# Remember to refresh the differentiator before attaching the new op
custom_dif.refresh()
differentiable_op = custom_dif.generate_differentiable_op(
sampled_op=expectation_sampled)
# Prep op inputs.
circuit_tensor = tfq.convert_to_tensor([my_circuit])
op_tensor = tfq.convert_to_tensor([[pauli_x]])
single_value = tf.convert_to_tensor([[my_alpha]])
num_samples_tensor = tf.convert_to_tensor([[5000]])
with tf.GradientTape() as g:
g.watch(single_value)
forward_output = differentiable_op(circuit_tensor, ['alpha'], single_value,
op_tensor, num_samples_tensor)
my_gradients = g.gradient(forward_output, single_value)
print('---TFQ---')
print('Foward: ', forward_output.numpy())
print('Gradient:', my_gradients.numpy())
print('---Original---')
print('Forward: ', my_expectation(pauli_x, my_alpha))
print('Gradient:', my_grad(pauli_x, my_alpha))
---TFQ--- Foward: [[0.8016]] Gradient: [[1.7932211]] ---Original--- Forward: 0.80901700258255 Gradient: 1.8063604831695557
