 Lihat di TensorFlow.org Lihat di TensorFlow.org |  Jalankan di Google Colab Jalankan di Google Colab |  Lihat sumber di GitHub Lihat sumber di GitHub |  Unduh buku catatan Unduh buku catatan |
Tutorial ini mengeksplorasi algoritma perhitungan gradien untuk nilai harapan sirkuit kuantum.
Menghitung gradien dari nilai ekspektasi dari sesuatu yang dapat diamati dalam sirkuit kuantum adalah proses yang terlibat. Nilai harapan dari yang dapat diamati tidak memiliki kemewahan memiliki rumus gradien analitik yang selalu mudah untuk dituliskan—tidak seperti transformasi pembelajaran mesin tradisional seperti perkalian matriks atau penjumlahan vektor yang memiliki rumus gradien analitik yang mudah untuk ditulis. Akibatnya, ada berbagai metode perhitungan gradien kuantum yang berguna untuk skenario yang berbeda. Tutorial ini membandingkan dan membedakan dua skema diferensiasi yang berbeda.
Mempersiapkan
pip install tensorflow==2.7.0
Instal TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Sekarang impor TensorFlow dan dependensi modul:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:25:24.733670: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Pendahuluan
Mari kita buat gagasan perhitungan gradien untuk sirkuit kuantum sedikit lebih konkret. Misalkan Anda memiliki rangkaian parameter seperti ini:
qubit = cirq.GridQubit(0, 0)
my_circuit = cirq.Circuit(cirq.Y(qubit)**sympy.Symbol('alpha'))
SVGCircuit(my_circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
Bersamaan dengan yang dapat diamati:
pauli_x = cirq.X(qubit)
pauli_x
cirq.X(cirq.GridQubit(0, 0))
Melihat operator ini, Anda tahu bahwa \(⟨Y(\alpha)| X | Y(\alpha)⟩ = \sin(\pi \alpha)\)
def my_expectation(op, alpha):
"""Compute ⟨Y(alpha)| `op` | Y(alpha)⟩"""
params = {'alpha': alpha}
sim = cirq.Simulator()
final_state_vector = sim.simulate(my_circuit, params).final_state_vector
return op.expectation_from_state_vector(final_state_vector, {qubit: 0}).real
my_alpha = 0.3
print("Expectation=", my_expectation(pauli_x, my_alpha))
print("Sin Formula=", np.sin(np.pi * my_alpha))
Expectation= 0.80901700258255 Sin Formula= 0.8090169943749475
dan jika Anda mendefinisikan \(f_{1}(\alpha) = ⟨Y(\alpha)| X | Y(\alpha)⟩\) lalu \(f_{1}^{'}(\alpha) = \pi \cos(\pi \alpha)\). Mari kita periksa ini:
def my_grad(obs, alpha, eps=0.01):
grad = 0
f_x = my_expectation(obs, alpha)
f_x_prime = my_expectation(obs, alpha + eps)
return ((f_x_prime - f_x) / eps).real
print('Finite difference:', my_grad(pauli_x, my_alpha))
print('Cosine formula: ', np.pi * np.cos(np.pi * my_alpha))
Finite difference: 1.8063604831695557 Cosine formula: 1.8465818304904567
2. Kebutuhan akan pembeda
Dengan sirkuit yang lebih besar, Anda tidak akan selalu beruntung memiliki rumus yang secara tepat menghitung gradien dari sirkuit kuantum tertentu. Jika rumus sederhana tidak cukup untuk menghitung gradien, kelas tfq.differentiators.Differentiator memungkinkan Anda menentukan algoritme untuk menghitung gradien sirkuit Anda. Misalnya, Anda dapat membuat ulang contoh di atas di TensorFlow Quantum (TFQ) dengan:
expectation_calculation = tfq.layers.Expectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=[[my_alpha]])
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.80901706]], dtype=float32)>
Namun, jika Anda beralih ke perkiraan ekspektasi berdasarkan pengambilan sampel (apa yang akan terjadi pada perangkat yang sebenarnya), nilainya dapat sedikit berubah. Ini berarti Anda sekarang memiliki perkiraan yang tidak sempurna:
sampled_expectation_calculation = tfq.layers.SampledExpectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
sampled_expectation_calculation(my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=[[my_alpha]])
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.836]], dtype=float32)>
Ini dapat dengan cepat menjadi masalah akurasi yang serius dalam hal gradien:
# Make input_points = [batch_size, 1] array.
input_points = np.linspace(0, 5, 200)[:, np.newaxis].astype(np.float32)
exact_outputs = expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=input_points)
imperfect_outputs = sampled_expectation_calculation(my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=input_points)
plt.title('Forward Pass Values')
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.plot(input_points, exact_outputs, label='Analytic')
plt.plot(input_points, imperfect_outputs, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07d556190>
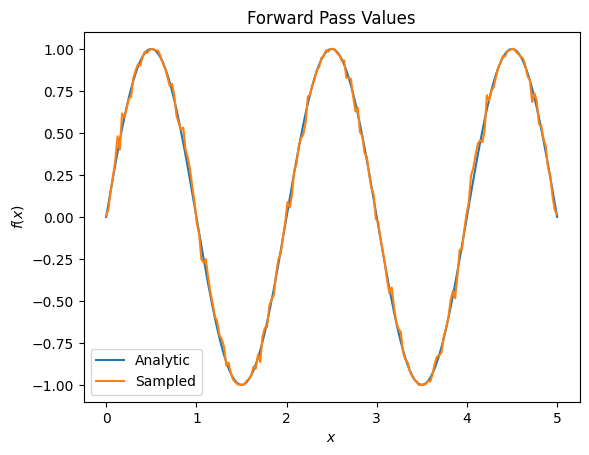
# Gradients are a much different story.
values_tensor = tf.convert_to_tensor(input_points)
with tf.GradientTape() as g:
g.watch(values_tensor)
exact_outputs = expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=values_tensor)
analytic_finite_diff_gradients = g.gradient(exact_outputs, values_tensor)
with tf.GradientTape() as g:
g.watch(values_tensor)
imperfect_outputs = sampled_expectation_calculation(
my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=values_tensor)
sampled_finite_diff_gradients = g.gradient(imperfect_outputs, values_tensor)
plt.title('Gradient Values')
plt.xlabel('$x$')
plt.ylabel('$f^{\'}(x)$')
plt.plot(input_points, analytic_finite_diff_gradients, label='Analytic')
plt.plot(input_points, sampled_finite_diff_gradients, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07adb8dd0>
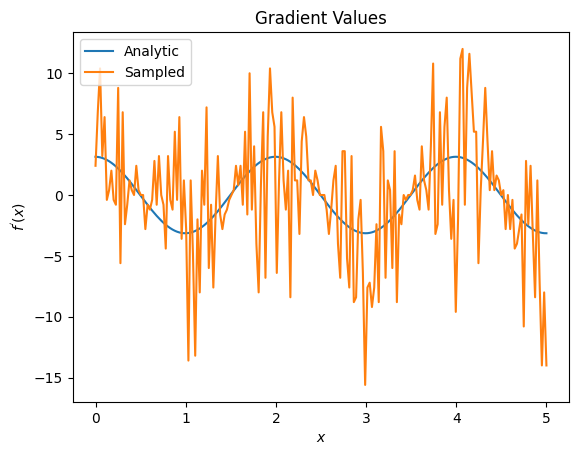
Di sini Anda dapat melihat bahwa meskipun rumus beda hingga cepat untuk menghitung gradien itu sendiri dalam kasus analitik, ketika sampai pada metode berbasis pengambilan sampel, itu terlalu berisik. Teknik yang lebih hati-hati harus digunakan untuk memastikan gradien yang baik dapat dihitung. Selanjutnya Anda akan melihat teknik yang jauh lebih lambat yang tidak akan cocok untuk perhitungan gradien ekspektasi analitis, tetapi kinerjanya jauh lebih baik dalam kasus berbasis sampel dunia nyata:
# A smarter differentiation scheme.
gradient_safe_sampled_expectation = tfq.layers.SampledExpectation(
differentiator=tfq.differentiators.ParameterShift())
with tf.GradientTape() as g:
g.watch(values_tensor)
imperfect_outputs = gradient_safe_sampled_expectation(
my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=values_tensor)
sampled_param_shift_gradients = g.gradient(imperfect_outputs, values_tensor)
plt.title('Gradient Values')
plt.xlabel('$x$')
plt.ylabel('$f^{\'}(x)$')
plt.plot(input_points, analytic_finite_diff_gradients, label='Analytic')
plt.plot(input_points, sampled_param_shift_gradients, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07ad9ff90>
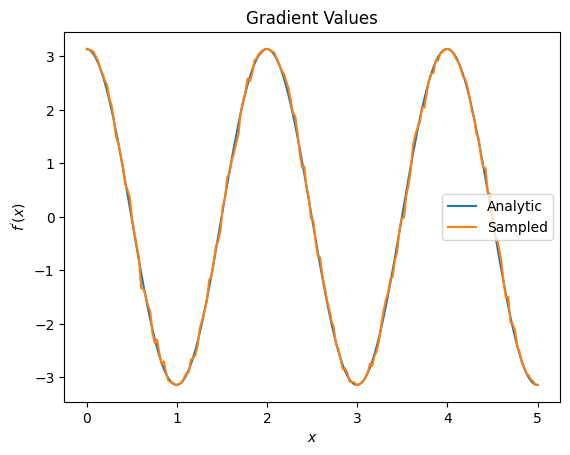
Dari penjelasan di atas Anda dapat melihat bahwa pembeda tertentu paling baik digunakan untuk skenario penelitian tertentu. Secara umum, metode berbasis sampel yang lebih lambat yang tahan terhadap kebisingan perangkat, dll., adalah pembeda yang hebat saat menguji atau mengimplementasikan algoritme dalam pengaturan yang lebih "dunia nyata". Metode yang lebih cepat seperti perbedaan hingga sangat bagus untuk perhitungan analitik dan Anda menginginkan throughput yang lebih tinggi, tetapi belum memperhatikan kelayakan perangkat dari algoritme Anda.
3. Beberapa yang dapat diamati
Mari perkenalkan observable kedua dan lihat bagaimana TensorFlow Quantum mendukung beberapa observable untuk satu sirkuit.
pauli_z = cirq.Z(qubit)
pauli_z
cirq.Z(cirq.GridQubit(0, 0))
Jika observable ini digunakan dengan sirkuit yang sama seperti sebelumnya, maka Anda memiliki \(f_{2}(\alpha) = ⟨Y(\alpha)| Z | Y(\alpha)⟩ = \cos(\pi \alpha)\) dan \(f_{2}^{'}(\alpha) = -\pi \sin(\pi \alpha)\). Lakukan pemeriksaan cepat:
test_value = 0.
print('Finite difference:', my_grad(pauli_z, test_value))
print('Sin formula: ', -np.pi * np.sin(np.pi * test_value))
Finite difference: -0.04934072494506836 Sin formula: -0.0
Ini pertandingan (cukup dekat).
Sekarang jika Anda mendefinisikan \(g(\alpha) = f_{1}(\alpha) + f_{2}(\alpha)\) lalu \(g'(\alpha) = f_{1}^{'}(\alpha) + f^{'}_{2}(\alpha)\). Mendefinisikan lebih dari satu yang dapat diamati di TensorFlow Quantum untuk digunakan bersama dengan sirkuit sama dengan menambahkan lebih banyak istilah ke \(g\).
Ini berarti bahwa gradien dari simbol tertentu dalam suatu rangkaian sama dengan jumlah gradien yang berkaitan dengan masing-masing yang dapat diamati untuk simbol yang diterapkan pada rangkaian itu. Ini kompatibel dengan pengambilan gradien TensorFlow dan backpropagation (di mana Anda memberikan jumlah gradien pada semua yang dapat diamati sebagai gradien untuk simbol tertentu).
sum_of_outputs = tfq.layers.Expectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
sum_of_outputs(my_circuit,
operators=[pauli_x, pauli_z],
symbol_names=['alpha'],
symbol_values=[[test_value]])
<tf.Tensor: shape=(1, 2), dtype=float32, numpy=array([[1.9106855e-15, 1.0000000e+00]], dtype=float32)>
Di sini Anda melihat entri pertama adalah harapan dengan Pauli X, dan yang kedua adalah harapan dengan Pauli Z. Sekarang ketika Anda mengambil gradien:
test_value_tensor = tf.convert_to_tensor([[test_value]])
with tf.GradientTape() as g:
g.watch(test_value_tensor)
outputs = sum_of_outputs(my_circuit,
operators=[pauli_x, pauli_z],
symbol_names=['alpha'],
symbol_values=test_value_tensor)
sum_of_gradients = g.gradient(outputs, test_value_tensor)
print(my_grad(pauli_x, test_value) + my_grad(pauli_z, test_value))
print(sum_of_gradients.numpy())
3.0917350202798843 [[3.0917213]]
Di sini Anda telah memverifikasi bahwa jumlah gradien untuk setiap yang dapat diamati memang gradien \(\alpha\). Perilaku ini didukung oleh semua pembeda TensorFlow Quantum dan memainkan peran penting dalam kompatibilitas dengan TensorFlow lainnya.
4. Penggunaan lanjutan
Semua pembeda yang ada di dalam subkelas TensorFlow Quantum tfq.differentiators.Differentiator . Untuk mengimplementasikan pembeda, pengguna harus mengimplementasikan salah satu dari dua antarmuka. Standarnya adalah mengimplementasikan get_gradient_circuits , yang memberi tahu kelas dasar sirkuit mana yang harus diukur untuk mendapatkan perkiraan gradien. Atau, Anda dapat membebani differentiate_analytic dan differentiate_sampled ; kelas tfq.differentiators.Adjoint mengambil rute ini.
Berikut ini menggunakan TensorFlow Quantum untuk mengimplementasikan gradien sirkuit. Anda akan menggunakan contoh kecil dari pergeseran parameter.
Ingat sirkuit yang Anda definisikan di atas, \(|\alpha⟩ = Y^{\alpha}|0⟩\). Seperti sebelumnya, Anda dapat mendefinisikan fungsi sebagai nilai ekspektasi dari rangkaian ini terhadap \(X\) dapat diamati, \(f(\alpha) = ⟨\alpha|X|\alpha⟩\). Menggunakan aturan pergeseran parameter , untuk rangkaian ini, Anda dapat menemukan bahwa turunannya adalah
\[\frac{\partial}{\partial \alpha} f(\alpha) = \frac{\pi}{2} f\left(\alpha + \frac{1}{2}\right) - \frac{ \pi}{2} f\left(\alpha - \frac{1}{2}\right)\]
Fungsi get_gradient_circuits mengembalikan komponen turunan ini.
class MyDifferentiator(tfq.differentiators.Differentiator):
"""A Toy differentiator for <Y^alpha | X |Y^alpha>."""
def __init__(self):
pass
def get_gradient_circuits(self, programs, symbol_names, symbol_values):
"""Return circuits to compute gradients for given forward pass circuits.
Every gradient on a quantum computer can be computed via measurements
of transformed quantum circuits. Here, you implement a custom gradient
for a specific circuit. For a real differentiator, you will need to
implement this function in a more general way. See the differentiator
implementations in the TFQ library for examples.
"""
# The two terms in the derivative are the same circuit...
batch_programs = tf.stack([programs, programs], axis=1)
# ... with shifted parameter values.
shift = tf.constant(1/2)
forward = symbol_values + shift
backward = symbol_values - shift
batch_symbol_values = tf.stack([forward, backward], axis=1)
# Weights are the coefficients of the terms in the derivative.
num_program_copies = tf.shape(batch_programs)[0]
batch_weights = tf.tile(tf.constant([[[np.pi/2, -np.pi/2]]]),
[num_program_copies, 1, 1])
# The index map simply says which weights go with which circuits.
batch_mapper = tf.tile(
tf.constant([[[0, 1]]]), [num_program_copies, 1, 1])
return (batch_programs, symbol_names, batch_symbol_values,
batch_weights, batch_mapper)
Kelas dasar Differentiator menggunakan komponen yang dikembalikan dari get_gradient_circuits untuk menghitung turunan, seperti dalam rumus pergeseran parameter yang Anda lihat di atas. Pembeda baru ini sekarang dapat digunakan dengan objek tfq.layer yang ada:
custom_dif = MyDifferentiator()
custom_grad_expectation = tfq.layers.Expectation(differentiator=custom_dif)
# Now let's get the gradients with finite diff.
with tf.GradientTape() as g:
g.watch(values_tensor)
exact_outputs = expectation_calculation(my_circuit,
operators=[pauli_x],
symbol_names=['alpha'],
symbol_values=values_tensor)
analytic_finite_diff_gradients = g.gradient(exact_outputs, values_tensor)
# Now let's get the gradients with custom diff.
with tf.GradientTape() as g:
g.watch(values_tensor)
my_outputs = custom_grad_expectation(my_circuit,
operators=[pauli_x],
symbol_names=['alpha'],
symbol_values=values_tensor)
my_gradients = g.gradient(my_outputs, values_tensor)
plt.subplot(1, 2, 1)
plt.title('Exact Gradient')
plt.plot(input_points, analytic_finite_diff_gradients.numpy())
plt.xlabel('x')
plt.ylabel('f(x)')
plt.subplot(1, 2, 2)
plt.title('My Gradient')
plt.plot(input_points, my_gradients.numpy())
plt.xlabel('x')
Text(0.5, 0, 'x')
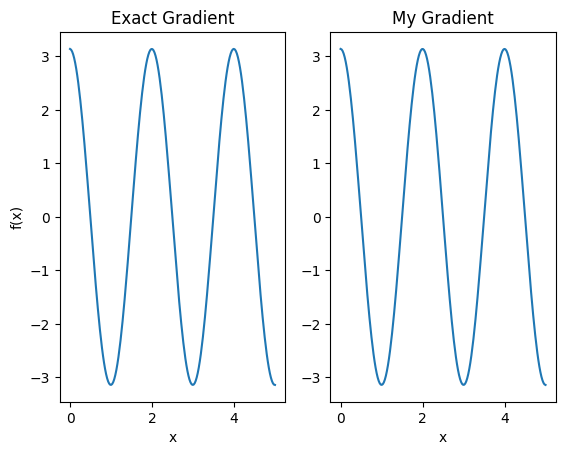
Diferensiator baru ini sekarang dapat digunakan untuk menghasilkan operasi yang dapat dibedakan.
# Create a noisy sample based expectation op.
expectation_sampled = tfq.get_sampled_expectation_op(
cirq.DensityMatrixSimulator(noise=cirq.depolarize(0.01)))
# Make it differentiable with your differentiator:
# Remember to refresh the differentiator before attaching the new op
custom_dif.refresh()
differentiable_op = custom_dif.generate_differentiable_op(
sampled_op=expectation_sampled)
# Prep op inputs.
circuit_tensor = tfq.convert_to_tensor([my_circuit])
op_tensor = tfq.convert_to_tensor([[pauli_x]])
single_value = tf.convert_to_tensor([[my_alpha]])
num_samples_tensor = tf.convert_to_tensor([[5000]])
with tf.GradientTape() as g:
g.watch(single_value)
forward_output = differentiable_op(circuit_tensor, ['alpha'], single_value,
op_tensor, num_samples_tensor)
my_gradients = g.gradient(forward_output, single_value)
print('---TFQ---')
print('Foward: ', forward_output.numpy())
print('Gradient:', my_gradients.numpy())
print('---Original---')
print('Forward: ', my_expectation(pauli_x, my_alpha))
print('Gradient:', my_grad(pauli_x, my_alpha))
---TFQ--- Foward: [[0.8016]] Gradient: [[1.7932211]] ---Original--- Forward: 0.80901700258255 Gradient: 1.8063604831695557
