 مشاهده در TensorFlow.org مشاهده در TensorFlow.org |  در Google Colab اجرا شود در Google Colab اجرا شود |  مشاهده منبع در GitHub مشاهده منبع در GitHub |  دانلود دفترچه یادداشت دانلود دفترچه یادداشت |
این آموزش الگوریتم های محاسبه گرادیان را برای مقادیر مورد انتظار مدارهای کوانتومی بررسی می کند.
محاسبه گرادیان مقدار انتظاری یک قابل مشاهده خاص در یک مدار کوانتومی یک فرآیند درگیر است. مقادیر انتظاری از قابل مشاهدهها، مجلل داشتن فرمولهای گرادیان تحلیلی را ندارند که همیشه به راحتی یادداشت میشوند - بر خلاف تبدیلهای یادگیری ماشین سنتی مانند ضرب ماتریس یا جمع برداری که دارای فرمولهای گرادیان تحلیلی هستند که به راحتی مینویسند. در نتیجه، روشهای متفاوتی برای محاسبه گرادیان کوانتومی وجود دارد که برای سناریوهای مختلف مفید است. این آموزش دو طرح تمایز متفاوت را با هم مقایسه و مقایسه می کند.
برپایی
pip install tensorflow==2.7.0
TensorFlow Quantum را نصب کنید:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
اکنون TensorFlow و وابستگی های ماژول را وارد کنید:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:25:24.733670: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. مقدماتی
بیایید مفهوم محاسبه گرادیان برای مدارهای کوانتومی را کمی دقیق تر کنیم. فرض کنید یک مدار پارامتری مانند این دارید:
qubit = cirq.GridQubit(0, 0)
my_circuit = cirq.Circuit(cirq.Y(qubit)**sympy.Symbol('alpha'))
SVGCircuit(my_circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
به همراه یک قابل مشاهده:
pauli_x = cirq.X(qubit)
pauli_x
cirq.X(cirq.GridQubit(0, 0))
با نگاهی به این عملگر، آن \(⟨Y(\alpha)| X | Y(\alpha)⟩ = \sin(\pi \alpha)\)را می شناسید
def my_expectation(op, alpha):
"""Compute ⟨Y(alpha)| `op` | Y(alpha)⟩"""
params = {'alpha': alpha}
sim = cirq.Simulator()
final_state_vector = sim.simulate(my_circuit, params).final_state_vector
return op.expectation_from_state_vector(final_state_vector, {qubit: 0}).real
my_alpha = 0.3
print("Expectation=", my_expectation(pauli_x, my_alpha))
print("Sin Formula=", np.sin(np.pi * my_alpha))
Expectation= 0.80901700258255 Sin Formula= 0.8090169943749475
و اگر l10n-placeholder2 را تعریف کنید، \(f_{1}(\alpha) = ⟨Y(\alpha)| X | Y(\alpha)⟩\) \(f_{1}^{'}(\alpha) = \pi \cos(\pi \alpha)\)تعریف کنید. بیایید این را بررسی کنیم:
def my_grad(obs, alpha, eps=0.01):
grad = 0
f_x = my_expectation(obs, alpha)
f_x_prime = my_expectation(obs, alpha + eps)
return ((f_x_prime - f_x) / eps).real
print('Finite difference:', my_grad(pauli_x, my_alpha))
print('Cosine formula: ', np.pi * np.cos(np.pi * my_alpha))
Finite difference: 1.8063604831695557 Cosine formula: 1.8465818304904567
2. نیاز به تمایز
با مدارهای بزرگتر، همیشه خوش شانس نخواهید بود که فرمولی داشته باشید که گرادیان های یک مدار کوانتومی معین را دقیقاً محاسبه کند. در صورتی که یک فرمول ساده برای محاسبه گرادیان کافی نباشد، کلاس tfq.differentiators.Differentiator به شما امکان می دهد الگوریتم هایی را برای محاسبه گرادیان مدارهای خود تعریف کنید. به عنوان مثال می توانید مثال بالا را در TensorFlow Quantum (TFQ) با استفاده از:
expectation_calculation = tfq.layers.Expectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=[[my_alpha]])
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.80901706]], dtype=float32)>
با این حال، اگر به تخمین انتظارات بر اساس نمونهگیری روی بیاورید (آنچه در یک دستگاه واقعی اتفاق میافتد)، مقادیر میتوانند کمی تغییر کنند. این بدان معناست که شما اکنون یک تخمین ناقص دارید:
sampled_expectation_calculation = tfq.layers.SampledExpectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
sampled_expectation_calculation(my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=[[my_alpha]])
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.836]], dtype=float32)>
این می تواند به سرعت به یک مشکل دقت جدی در هنگام گرادیان تبدیل شود:
# Make input_points = [batch_size, 1] array.
input_points = np.linspace(0, 5, 200)[:, np.newaxis].astype(np.float32)
exact_outputs = expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=input_points)
imperfect_outputs = sampled_expectation_calculation(my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=input_points)
plt.title('Forward Pass Values')
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.plot(input_points, exact_outputs, label='Analytic')
plt.plot(input_points, imperfect_outputs, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07d556190>
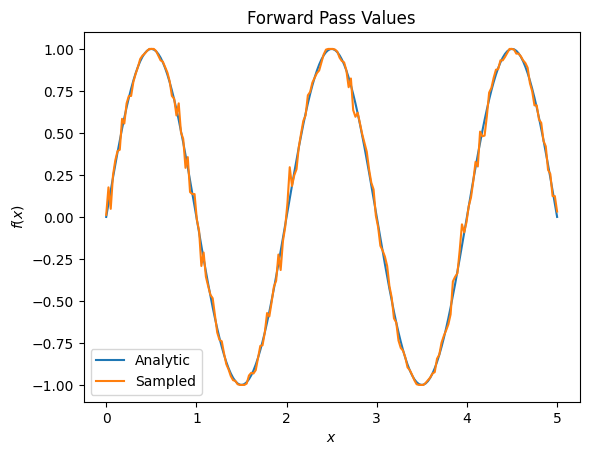
# Gradients are a much different story.
values_tensor = tf.convert_to_tensor(input_points)
with tf.GradientTape() as g:
g.watch(values_tensor)
exact_outputs = expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=values_tensor)
analytic_finite_diff_gradients = g.gradient(exact_outputs, values_tensor)
with tf.GradientTape() as g:
g.watch(values_tensor)
imperfect_outputs = sampled_expectation_calculation(
my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=values_tensor)
sampled_finite_diff_gradients = g.gradient(imperfect_outputs, values_tensor)
plt.title('Gradient Values')
plt.xlabel('$x$')
plt.ylabel('$f^{\'}(x)$')
plt.plot(input_points, analytic_finite_diff_gradients, label='Analytic')
plt.plot(input_points, sampled_finite_diff_gradients, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07adb8dd0>
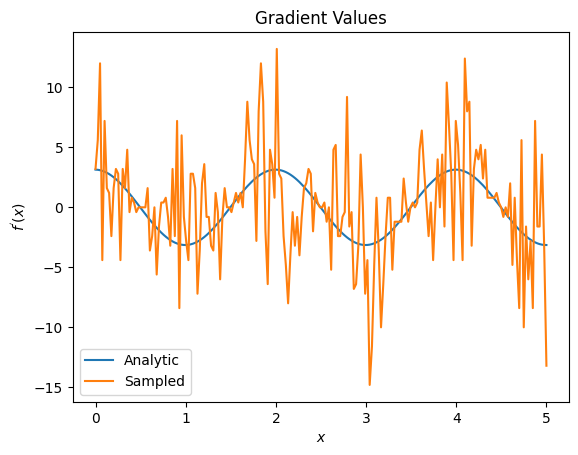
در اینجا میتوانید ببینید که اگرچه فرمول تفاضل محدود برای محاسبه خود شیبها در حالت تحلیلی سریع است، اما زمانی که به روشهای مبتنی بر نمونهگیری میرسید، بسیار پر سر و صدا بود. برای اطمینان از محاسبه گرادیان خوب باید از تکنیک های دقیق تری استفاده شود. در ادامه به یک تکنیک بسیار کندتر نگاه خواهید کرد که برای محاسبات گرادیان انتظارات تحلیلی مناسب نیست، اما در مورد مبتنی بر نمونه واقعی بسیار بهتر عمل می کند:
# A smarter differentiation scheme.
gradient_safe_sampled_expectation = tfq.layers.SampledExpectation(
differentiator=tfq.differentiators.ParameterShift())
with tf.GradientTape() as g:
g.watch(values_tensor)
imperfect_outputs = gradient_safe_sampled_expectation(
my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=values_tensor)
sampled_param_shift_gradients = g.gradient(imperfect_outputs, values_tensor)
plt.title('Gradient Values')
plt.xlabel('$x$')
plt.ylabel('$f^{\'}(x)$')
plt.plot(input_points, analytic_finite_diff_gradients, label='Analytic')
plt.plot(input_points, sampled_param_shift_gradients, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07ad9ff90>
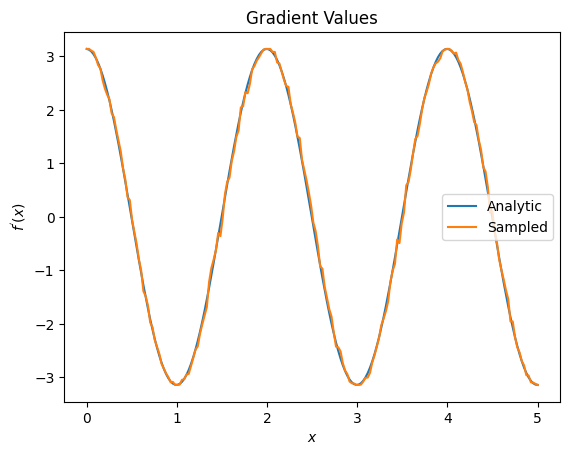
از موارد فوق می توانید ببینید که تمایز دهنده های خاص به بهترین وجه برای سناریوهای تحقیقاتی خاص استفاده می شوند. به طور کلی، روشهای آهستهتر مبتنی بر نمونه که نسبت به نویز دستگاه و غیره قویتر هستند، هنگام آزمایش یا پیادهسازی الگوریتمها در محیطی «دنیای واقعی»، تمایزات بسیار خوبی دارند. روشهای سریعتر مانند تفاضل محدود برای محاسبات تحلیلی عالی هستند و شما میخواهید توان عملیاتی بالاتری داشته باشید، اما هنوز نگران قابلیتپذیری دستگاه الگوریتم خود نیستید.
3. قابل مشاهده های متعدد
بیایید یک قابل مشاهده دوم را معرفی کنیم و ببینیم که چگونه TensorFlow Quantum از چندین مشاهده پذیر برای یک مدار پشتیبانی می کند.
pauli_z = cirq.Z(qubit)
pauli_z
cirq.Z(cirq.GridQubit(0, 0))
اگر این قابل مشاهده با همان مدار قبلی استفاده شود، در این صورت شما \(f_{2}(\alpha) = ⟨Y(\alpha)| Z | Y(\alpha)⟩ = \cos(\pi \alpha)\) و \(f_{2}^{'}(\alpha) = -\pi \sin(\pi \alpha)\)دارید. یک بررسی سریع انجام دهید:
test_value = 0.
print('Finite difference:', my_grad(pauli_z, test_value))
print('Sin formula: ', -np.pi * np.sin(np.pi * test_value))
Finite difference: -0.04934072494506836 Sin formula: -0.0
این یک مسابقه است (به اندازه کافی نزدیک).
حالا اگر l10n-placeholder6 را تعریف کنید، \(g(\alpha) = f_{1}(\alpha) + f_{2}(\alpha)\) \(g'(\alpha) = f_{1}^{'}(\alpha) + f^{'}_{2}(\alpha)\)تعریف کنید. تعریف بیش از یک قابل مشاهده در TensorFlow Quantum برای استفاده همراه با یک مدار معادل افزودن شرایط بیشتری به \(g\)است.
این بدان معناست که گرادیان یک نماد خاص در یک مدار برابر است با مجموع گرادیان ها نسبت به هر قابل مشاهده برای آن نماد اعمال شده در آن مدار. این با گرفتن گرادیان TensorFlow و پس انتشار (که در آن مجموع گرادیان ها را بر روی همه مشاهده پذیرها به عنوان گرادیان برای یک نماد خاص می دهید) سازگار است.
sum_of_outputs = tfq.layers.Expectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
sum_of_outputs(my_circuit,
operators=[pauli_x, pauli_z],
symbol_names=['alpha'],
symbol_values=[[test_value]])
<tf.Tensor: shape=(1, 2), dtype=float32, numpy=array([[1.9106855e-15, 1.0000000e+00]], dtype=float32)>
در اینجا میبینید که اولین ورودی انتظار wrt Pauli X است، و دومی انتظار wrt Pauli Z است. حالا وقتی گرادیان را میگیرید:
test_value_tensor = tf.convert_to_tensor([[test_value]])
with tf.GradientTape() as g:
g.watch(test_value_tensor)
outputs = sum_of_outputs(my_circuit,
operators=[pauli_x, pauli_z],
symbol_names=['alpha'],
symbol_values=test_value_tensor)
sum_of_gradients = g.gradient(outputs, test_value_tensor)
print(my_grad(pauli_x, test_value) + my_grad(pauli_z, test_value))
print(sum_of_gradients.numpy())
3.0917350202798843 [[3.0917213]]
در اینجا شما تأیید کردهاید که مجموع گرادیانها برای هر قابل مشاهده در واقع گرادیان \(\alpha\)است. این رفتار توسط همه تمایز دهنده های کوانتومی TensorFlow پشتیبانی می شود و نقش مهمی در سازگاری با بقیه TensorFlow ایفا می کند.
4. استفاده پیشرفته
همه متمایز کننده هایی که در زیر کلاس TensorFlow Quantum tfq.differentiators.Differentiator وجود دارند. برای پیاده سازی دیفرانسیل، کاربر باید یکی از دو رابط را پیاده سازی کند. استاندارد پیادهسازی get_gradient_circuits است که به کلاس پایه میگوید کدام مدارها را اندازهگیری کند تا برآوردی از گرادیان بدست آید. از طرف دیگر، میتوانید differentiate_analytic و differentiate_sampled را اضافه بار کنید. کلاس tfq.differentiators.Adjoint این مسیر را طی می کند.
در زیر از TensorFlow Quantum برای پیاده سازی گرادیان مدار استفاده می شود. شما از یک مثال کوچک از تغییر پارامتر استفاده خواهید کرد.
مداری را که در بالا تعریف کردید، \(|\alpha⟩ = Y^{\alpha}|0⟩\)به یاد بیاورید. مانند قبل، می توانید تابعی را به عنوان مقدار انتظاری این مدار در برابر \(X\) قابل مشاهده، \(f(\alpha) = ⟨\alpha|X|\alpha⟩\)تعریف کنید. با استفاده از قوانین تغییر پارامتر ، برای این مدار، می توانید دریابید که مشتق شده است
\[\frac{\partial}{\partial \alpha} f(\alpha) = \frac{\pi}{2} f\left(\alpha + \frac{1}{2}\right) - \frac{ \pi}{2} f\left(\alpha - \frac{1}{2}\right)\]
تابع get_gradient_circuits اجزای این مشتق را برمی گرداند.
class MyDifferentiator(tfq.differentiators.Differentiator):
"""A Toy differentiator for <Y^alpha | X |Y^alpha>."""
def __init__(self):
pass
def get_gradient_circuits(self, programs, symbol_names, symbol_values):
"""Return circuits to compute gradients for given forward pass circuits.
Every gradient on a quantum computer can be computed via measurements
of transformed quantum circuits. Here, you implement a custom gradient
for a specific circuit. For a real differentiator, you will need to
implement this function in a more general way. See the differentiator
implementations in the TFQ library for examples.
"""
# The two terms in the derivative are the same circuit...
batch_programs = tf.stack([programs, programs], axis=1)
# ... with shifted parameter values.
shift = tf.constant(1/2)
forward = symbol_values + shift
backward = symbol_values - shift
batch_symbol_values = tf.stack([forward, backward], axis=1)
# Weights are the coefficients of the terms in the derivative.
num_program_copies = tf.shape(batch_programs)[0]
batch_weights = tf.tile(tf.constant([[[np.pi/2, -np.pi/2]]]),
[num_program_copies, 1, 1])
# The index map simply says which weights go with which circuits.
batch_mapper = tf.tile(
tf.constant([[[0, 1]]]), [num_program_copies, 1, 1])
return (batch_programs, symbol_names, batch_symbol_values,
batch_weights, batch_mapper)
کلاس پایه Differentiator از مولفه های برگشتی از get_gradient_circuits برای محاسبه مشتق استفاده می کند، همانطور که در فرمول تغییر پارامتر که در بالا دیدید. این متمایز کننده جدید اکنون می تواند با اشیاء tfq.layer موجود استفاده شود:
custom_dif = MyDifferentiator()
custom_grad_expectation = tfq.layers.Expectation(differentiator=custom_dif)
# Now let's get the gradients with finite diff.
with tf.GradientTape() as g:
g.watch(values_tensor)
exact_outputs = expectation_calculation(my_circuit,
operators=[pauli_x],
symbol_names=['alpha'],
symbol_values=values_tensor)
analytic_finite_diff_gradients = g.gradient(exact_outputs, values_tensor)
# Now let's get the gradients with custom diff.
with tf.GradientTape() as g:
g.watch(values_tensor)
my_outputs = custom_grad_expectation(my_circuit,
operators=[pauli_x],
symbol_names=['alpha'],
symbol_values=values_tensor)
my_gradients = g.gradient(my_outputs, values_tensor)
plt.subplot(1, 2, 1)
plt.title('Exact Gradient')
plt.plot(input_points, analytic_finite_diff_gradients.numpy())
plt.xlabel('x')
plt.ylabel('f(x)')
plt.subplot(1, 2, 2)
plt.title('My Gradient')
plt.plot(input_points, my_gradients.numpy())
plt.xlabel('x')
Text(0.5, 0, 'x')
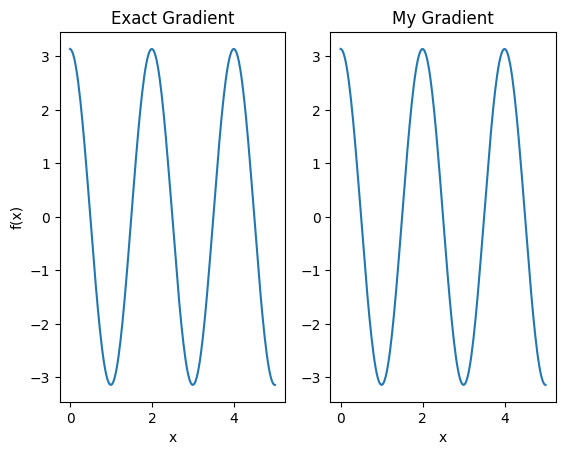
این متمایز کننده جدید اکنون می تواند برای تولید عملیات های متمایز استفاده شود.
# Create a noisy sample based expectation op.
expectation_sampled = tfq.get_sampled_expectation_op(
cirq.DensityMatrixSimulator(noise=cirq.depolarize(0.01)))
# Make it differentiable with your differentiator:
# Remember to refresh the differentiator before attaching the new op
custom_dif.refresh()
differentiable_op = custom_dif.generate_differentiable_op(
sampled_op=expectation_sampled)
# Prep op inputs.
circuit_tensor = tfq.convert_to_tensor([my_circuit])
op_tensor = tfq.convert_to_tensor([[pauli_x]])
single_value = tf.convert_to_tensor([[my_alpha]])
num_samples_tensor = tf.convert_to_tensor([[5000]])
with tf.GradientTape() as g:
g.watch(single_value)
forward_output = differentiable_op(circuit_tensor, ['alpha'], single_value,
op_tensor, num_samples_tensor)
my_gradients = g.gradient(forward_output, single_value)
print('---TFQ---')
print('Foward: ', forward_output.numpy())
print('Gradient:', my_gradients.numpy())
print('---Original---')
print('Forward: ', my_expectation(pauli_x, my_alpha))
print('Gradient:', my_grad(pauli_x, my_alpha))
---TFQ--- Foward: [[0.8016]] Gradient: [[1.7932211]] ---Original--- Forward: 0.80901700258255 Gradient: 1.8063604831695557
