 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar libreta Descargar libreta |
Este tutorial explora los algoritmos de cálculo de gradientes para los valores esperados de los circuitos cuánticos.
Calcular el gradiente del valor esperado de un cierto observable en un circuito cuántico es un proceso complicado. Los valores esperados de los observables no pueden darse el lujo de tener fórmulas de gradiente analítico que siempre son fáciles de escribir, a diferencia de las transformaciones de aprendizaje automático tradicionales, como la multiplicación de matrices o la suma de vectores, que tienen fórmulas de gradiente analítico que son fáciles de escribir. Como resultado, existen diferentes métodos de cálculo de gradiente cuántico que son útiles para diferentes escenarios. Este tutorial compara y contrasta dos esquemas de diferenciación diferentes.
Configuración
pip install tensorflow==2.7.0
Instale TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Ahora importa TensorFlow y las dependencias del módulo:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:25:24.733670: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Preliminar
Hagamos un poco más concreta la noción de cálculo de gradiente para circuitos cuánticos. Suponga que tiene un circuito parametrizado como este:
qubit = cirq.GridQubit(0, 0)
my_circuit = cirq.Circuit(cirq.Y(qubit)**sympy.Symbol('alpha'))
SVGCircuit(my_circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
Junto con un observable:
pauli_x = cirq.X(qubit)
pauli_x
cirq.X(cirq.GridQubit(0, 0))
Al observar este operador, sabe que \(⟨Y(\alpha)| X | Y(\alpha)⟩ = \sin(\pi \alpha)\)
def my_expectation(op, alpha):
"""Compute ⟨Y(alpha)| `op` | Y(alpha)⟩"""
params = {'alpha': alpha}
sim = cirq.Simulator()
final_state_vector = sim.simulate(my_circuit, params).final_state_vector
return op.expectation_from_state_vector(final_state_vector, {qubit: 0}).real
my_alpha = 0.3
print("Expectation=", my_expectation(pauli_x, my_alpha))
print("Sin Formula=", np.sin(np.pi * my_alpha))
Expectation= 0.80901700258255 Sin Formula= 0.8090169943749475
y si define \(f_{1}(\alpha) = ⟨Y(\alpha)| X | Y(\alpha)⟩\) entonces \(f_{1}^{'}(\alpha) = \pi \cos(\pi \alpha)\). Comprobemos esto:
def my_grad(obs, alpha, eps=0.01):
grad = 0
f_x = my_expectation(obs, alpha)
f_x_prime = my_expectation(obs, alpha + eps)
return ((f_x_prime - f_x) / eps).real
print('Finite difference:', my_grad(pauli_x, my_alpha))
print('Cosine formula: ', np.pi * np.cos(np.pi * my_alpha))
Finite difference: 1.8063604831695557 Cosine formula: 1.8465818304904567
2. La necesidad de un diferenciador
Con circuitos más grandes, no siempre tendrás la suerte de tener una fórmula que calcule con precisión los gradientes de un circuito cuántico dado. En el caso de que una fórmula simple no sea suficiente para calcular el gradiente, la clase tfq.differentiators.Differentiator le permite definir algoritmos para calcular los gradientes de sus circuitos. Por ejemplo, puede recrear el ejemplo anterior en TensorFlow Quantum (TFQ) con:
expectation_calculation = tfq.layers.Expectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=[[my_alpha]])
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.80901706]], dtype=float32)>
Sin embargo, si cambia a estimar la expectativa basada en el muestreo (lo que sucedería en un dispositivo real), los valores pueden cambiar un poco. Esto significa que ahora tiene una estimación imperfecta:
sampled_expectation_calculation = tfq.layers.SampledExpectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
sampled_expectation_calculation(my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=[[my_alpha]])
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.836]], dtype=float32)>
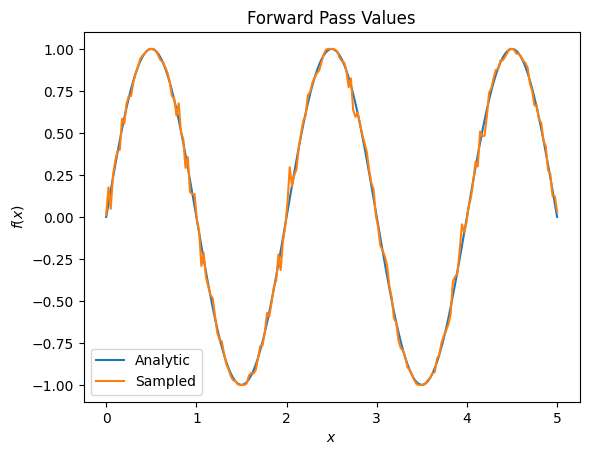
Esto puede convertirse rápidamente en un grave problema de precisión cuando se trata de gradientes:
# Make input_points = [batch_size, 1] array.
input_points = np.linspace(0, 5, 200)[:, np.newaxis].astype(np.float32)
exact_outputs = expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=input_points)
imperfect_outputs = sampled_expectation_calculation(my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=input_points)
plt.title('Forward Pass Values')
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.plot(input_points, exact_outputs, label='Analytic')
plt.plot(input_points, imperfect_outputs, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07d556190>
# Gradients are a much different story.
values_tensor = tf.convert_to_tensor(input_points)
with tf.GradientTape() as g:
g.watch(values_tensor)
exact_outputs = expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=values_tensor)
analytic_finite_diff_gradients = g.gradient(exact_outputs, values_tensor)
with tf.GradientTape() as g:
g.watch(values_tensor)
imperfect_outputs = sampled_expectation_calculation(
my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=values_tensor)
sampled_finite_diff_gradients = g.gradient(imperfect_outputs, values_tensor)
plt.title('Gradient Values')
plt.xlabel('$x$')
plt.ylabel('$f^{\'}(x)$')
plt.plot(input_points, analytic_finite_diff_gradients, label='Analytic')
plt.plot(input_points, sampled_finite_diff_gradients, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07adb8dd0>
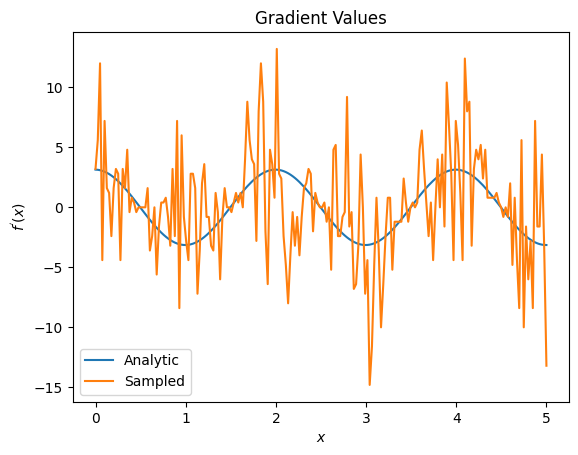
Aquí puede ver que, aunque la fórmula de diferencia finita es rápida para calcular los gradientes en el caso analítico, cuando se trataba de métodos basados en muestreo, era demasiado ruidosa. Se deben usar técnicas más cuidadosas para asegurar que se pueda calcular un buen gradiente. A continuación, verá una técnica mucho más lenta que no sería tan adecuada para los cálculos analíticos del gradiente esperado, pero que funciona mucho mejor en el caso basado en muestras del mundo real:
# A smarter differentiation scheme.
gradient_safe_sampled_expectation = tfq.layers.SampledExpectation(
differentiator=tfq.differentiators.ParameterShift())
with tf.GradientTape() as g:
g.watch(values_tensor)
imperfect_outputs = gradient_safe_sampled_expectation(
my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=values_tensor)
sampled_param_shift_gradients = g.gradient(imperfect_outputs, values_tensor)
plt.title('Gradient Values')
plt.xlabel('$x$')
plt.ylabel('$f^{\'}(x)$')
plt.plot(input_points, analytic_finite_diff_gradients, label='Analytic')
plt.plot(input_points, sampled_param_shift_gradients, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07ad9ff90>
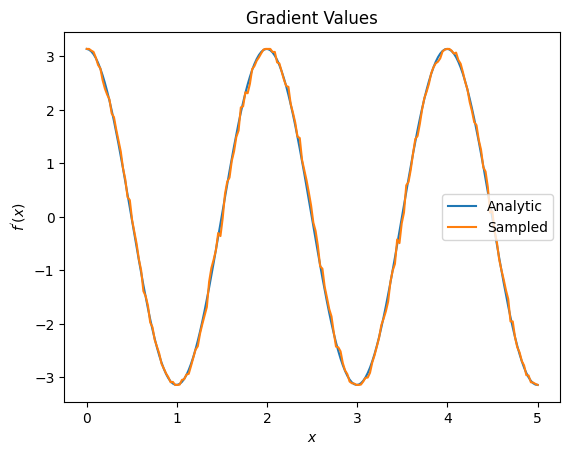
De lo anterior, puede ver que ciertos diferenciadores se utilizan mejor para escenarios de investigación particulares. En general, los métodos más lentos basados en muestras que son resistentes al ruido del dispositivo, etc., son grandes diferenciadores cuando se prueban o implementan algoritmos en un entorno más "real". Los métodos más rápidos, como la diferencia finita, son excelentes para los cálculos analíticos y desea un mayor rendimiento, pero aún no le preocupa la viabilidad del dispositivo de su algoritmo.
3. Múltiples observables
Presentemos un segundo observable y veamos cómo TensorFlow Quantum admite varios observables para un solo circuito.
pauli_z = cirq.Z(qubit)
pauli_z
cirq.Z(cirq.GridQubit(0, 0))
Si este observable se usa con el mismo circuito que antes, entonces tiene \(f_{2}(\alpha) = ⟨Y(\alpha)| Z | Y(\alpha)⟩ = \cos(\pi \alpha)\) y \(f_{2}^{'}(\alpha) = -\pi \sin(\pi \alpha)\). Realice una comprobación rápida:
test_value = 0.
print('Finite difference:', my_grad(pauli_z, test_value))
print('Sin formula: ', -np.pi * np.sin(np.pi * test_value))
Finite difference: -0.04934072494506836 Sin formula: -0.0
Es un partido (lo suficientemente cerca).
Ahora, si define \(g(\alpha) = f_{1}(\alpha) + f_{2}(\alpha)\) entonces \(g'(\alpha) = f_{1}^{'}(\alpha) + f^{'}_{2}(\alpha)\). Definir más de un observable en TensorFlow Quantum para usarlo junto con un circuito equivale a agregar más términos a \(g\).
Esto significa que el gradiente de un símbolo particular en un circuito es igual a la suma de los gradientes con respecto a cada observable para ese símbolo aplicado a ese circuito. Esto es compatible con la toma de gradiente y la retropropagación de TensorFlow (donde proporciona la suma de los gradientes sobre todos los observables como el gradiente de un símbolo en particular).
sum_of_outputs = tfq.layers.Expectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
sum_of_outputs(my_circuit,
operators=[pauli_x, pauli_z],
symbol_names=['alpha'],
symbol_values=[[test_value]])
<tf.Tensor: shape=(1, 2), dtype=float32, numpy=array([[1.9106855e-15, 1.0000000e+00]], dtype=float32)>
Aquí puede ver que la primera entrada es la expectativa con Pauli X, y la segunda es la expectativa con Pauli Z. Ahora, cuando toma el degradado:
test_value_tensor = tf.convert_to_tensor([[test_value]])
with tf.GradientTape() as g:
g.watch(test_value_tensor)
outputs = sum_of_outputs(my_circuit,
operators=[pauli_x, pauli_z],
symbol_names=['alpha'],
symbol_values=test_value_tensor)
sum_of_gradients = g.gradient(outputs, test_value_tensor)
print(my_grad(pauli_x, test_value) + my_grad(pauli_z, test_value))
print(sum_of_gradients.numpy())
3.0917350202798843 [[3.0917213]]
Aquí ha verificado que la suma de los gradientes para cada observable es, de hecho, el gradiente de \(\alpha\). Este comportamiento es compatible con todos los diferenciadores de TensorFlow Quantum y juega un papel crucial en la compatibilidad con el resto de TensorFlow.
4. Uso avanzado
Todos los diferenciadores que existen dentro de la subclase TensorFlow Quantum tfq.differentiators.Differentiator . differentiators.Differentiator . Para implementar un diferenciador, un usuario debe implementar una de dos interfaces. El estándar es implementar get_gradient_circuits , que le dice a la clase base qué circuitos medir para obtener una estimación del gradiente. Alternativamente, puede sobrecargar differentiate_analytic y differentiate_sampled ; la clase tfq.differentiators.Adjoint toma esta ruta.
Lo siguiente usa TensorFlow Quantum para implementar el gradiente de un circuito. Utilizará un pequeño ejemplo de cambio de parámetros.
Recuerda el circuito que definiste anteriormente, \(|\alpha⟩ = Y^{\alpha}|0⟩\). Como antes, puede definir una función como el valor esperado de este circuito contra el observable l10n- \(X\) , \(f(\alpha) = ⟨\alpha|X|\alpha⟩\). Usando reglas de cambio de parámetros , para este circuito, puede encontrar que la derivada es
\[\frac{\partial}{\partial \alpha} f(\alpha) = \frac{\pi}{2} f\left(\alpha + \frac{1}{2}\right) - \frac{ \pi}{2} f\left(\alpha - \frac{1}{2}\right)\]
La función get_gradient_circuits devuelve los componentes de esta derivada.
class MyDifferentiator(tfq.differentiators.Differentiator):
"""A Toy differentiator for <Y^alpha | X |Y^alpha>."""
def __init__(self):
pass
def get_gradient_circuits(self, programs, symbol_names, symbol_values):
"""Return circuits to compute gradients for given forward pass circuits.
Every gradient on a quantum computer can be computed via measurements
of transformed quantum circuits. Here, you implement a custom gradient
for a specific circuit. For a real differentiator, you will need to
implement this function in a more general way. See the differentiator
implementations in the TFQ library for examples.
"""
# The two terms in the derivative are the same circuit...
batch_programs = tf.stack([programs, programs], axis=1)
# ... with shifted parameter values.
shift = tf.constant(1/2)
forward = symbol_values + shift
backward = symbol_values - shift
batch_symbol_values = tf.stack([forward, backward], axis=1)
# Weights are the coefficients of the terms in the derivative.
num_program_copies = tf.shape(batch_programs)[0]
batch_weights = tf.tile(tf.constant([[[np.pi/2, -np.pi/2]]]),
[num_program_copies, 1, 1])
# The index map simply says which weights go with which circuits.
batch_mapper = tf.tile(
tf.constant([[[0, 1]]]), [num_program_copies, 1, 1])
return (batch_programs, symbol_names, batch_symbol_values,
batch_weights, batch_mapper)
La clase base de Differentiator usa los componentes devueltos por get_gradient_circuits para calcular la derivada, como en la fórmula de cambio de parámetro que viste arriba. Este nuevo diferenciador ahora se puede usar con objetos tfq.layer existentes:
custom_dif = MyDifferentiator()
custom_grad_expectation = tfq.layers.Expectation(differentiator=custom_dif)
# Now let's get the gradients with finite diff.
with tf.GradientTape() as g:
g.watch(values_tensor)
exact_outputs = expectation_calculation(my_circuit,
operators=[pauli_x],
symbol_names=['alpha'],
symbol_values=values_tensor)
analytic_finite_diff_gradients = g.gradient(exact_outputs, values_tensor)
# Now let's get the gradients with custom diff.
with tf.GradientTape() as g:
g.watch(values_tensor)
my_outputs = custom_grad_expectation(my_circuit,
operators=[pauli_x],
symbol_names=['alpha'],
symbol_values=values_tensor)
my_gradients = g.gradient(my_outputs, values_tensor)
plt.subplot(1, 2, 1)
plt.title('Exact Gradient')
plt.plot(input_points, analytic_finite_diff_gradients.numpy())
plt.xlabel('x')
plt.ylabel('f(x)')
plt.subplot(1, 2, 2)
plt.title('My Gradient')
plt.plot(input_points, my_gradients.numpy())
plt.xlabel('x')
Text(0.5, 0, 'x')
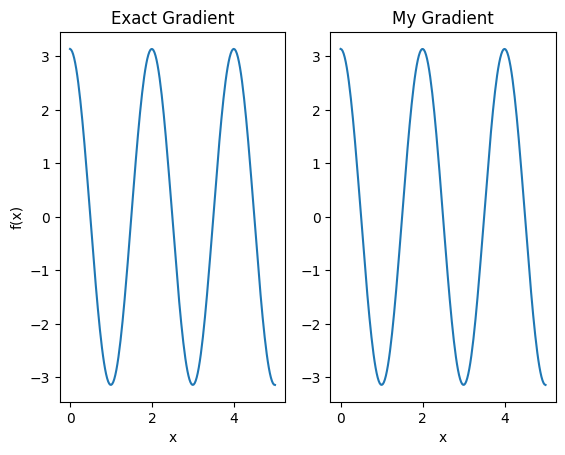
Este nuevo diferenciador ahora se puede usar para generar operaciones diferenciables.
# Create a noisy sample based expectation op.
expectation_sampled = tfq.get_sampled_expectation_op(
cirq.DensityMatrixSimulator(noise=cirq.depolarize(0.01)))
# Make it differentiable with your differentiator:
# Remember to refresh the differentiator before attaching the new op
custom_dif.refresh()
differentiable_op = custom_dif.generate_differentiable_op(
sampled_op=expectation_sampled)
# Prep op inputs.
circuit_tensor = tfq.convert_to_tensor([my_circuit])
op_tensor = tfq.convert_to_tensor([[pauli_x]])
single_value = tf.convert_to_tensor([[my_alpha]])
num_samples_tensor = tf.convert_to_tensor([[5000]])
with tf.GradientTape() as g:
g.watch(single_value)
forward_output = differentiable_op(circuit_tensor, ['alpha'], single_value,
op_tensor, num_samples_tensor)
my_gradients = g.gradient(forward_output, single_value)
print('---TFQ---')
print('Foward: ', forward_output.numpy())
print('Gradient:', my_gradients.numpy())
print('---Original---')
print('Forward: ', my_expectation(pauli_x, my_alpha))
print('Gradient:', my_grad(pauli_x, my_alpha))
---TFQ--- Foward: [[0.8016]] Gradient: [[1.7932211]] ---Original--- Forward: 0.80901700258255 Gradient: 1.8063604831695557
