 TensorFlow.org এ দেখুন TensorFlow.org এ দেখুন |  Google Colab-এ চালান Google Colab-এ চালান |  GitHub-এ উৎস দেখুন GitHub-এ উৎস দেখুন |  নোটবুক ডাউনলোড করুন নোটবুক ডাউনলোড করুন |
এই টিউটোরিয়ালটি কোয়ান্টাম সার্কিটের প্রত্যাশার মানগুলির জন্য গ্রেডিয়েন্ট গণনা অ্যালগরিদমগুলি অন্বেষণ করে।
একটি কোয়ান্টাম সার্কিটে একটি নির্দিষ্ট পর্যবেক্ষণযোগ্য প্রত্যাশিত মানের গ্রেডিয়েন্ট গণনা করা একটি জড়িত প্রক্রিয়া। পর্যবেক্ষণযোগ্যগুলির প্রত্যাশার মানগুলিতে বিশ্লেষণাত্মক গ্রেডিয়েন্ট সূত্র থাকার বিলাসিতা নেই যেগুলি সর্বদাই সহজে লিখতে হয় - প্রথাগত মেশিন লার্নিং রূপান্তরগুলির বিপরীতে যেমন ম্যাট্রিক্স গুণ বা ভেক্টর সংযোজন যাতে বিশ্লেষণাত্মক গ্রেডিয়েন্ট সূত্র থাকে যা লেখা সহজ। ফলস্বরূপ, বিভিন্ন কোয়ান্টাম গ্রেডিয়েন্ট গণনা পদ্ধতি রয়েছে যা বিভিন্ন পরিস্থিতিতে কাজে আসে। এই টিউটোরিয়াল দুটি ভিন্ন ভিন্নতা স্কিম তুলনা এবং বৈসাদৃশ্য.
সেটআপ
pip install tensorflow==2.7.0
টেনসরফ্লো কোয়ান্টাম ইনস্টল করুন:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
এখন TensorFlow এবং মডিউল নির্ভরতা আমদানি করুন:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:25:24.733670: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. প্রাথমিক
কোয়ান্টাম সার্কিটগুলির জন্য গ্রেডিয়েন্ট গণনার ধারণাটিকে আরও একটু কংক্রিট করা যাক। ধরুন আপনার কাছে এইরকম একটি প্যারামিটারাইজড সার্কিট আছে:
qubit = cirq.GridQubit(0, 0)
my_circuit = cirq.Circuit(cirq.Y(qubit)**sympy.Symbol('alpha'))
SVGCircuit(my_circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
একটি পর্যবেক্ষণযোগ্য সহ:
pauli_x = cirq.X(qubit)
pauli_x
cirq.X(cirq.GridQubit(0, 0))
এই অপারেটরের দিকে তাকিয়ে আপনি জানেন যে \(⟨Y(\alpha)| X | Y(\alpha)⟩ = \sin(\pi \alpha)\)
def my_expectation(op, alpha):
"""Compute ⟨Y(alpha)| `op` | Y(alpha)⟩"""
params = {'alpha': alpha}
sim = cirq.Simulator()
final_state_vector = sim.simulate(my_circuit, params).final_state_vector
return op.expectation_from_state_vector(final_state_vector, {qubit: 0}).real
my_alpha = 0.3
print("Expectation=", my_expectation(pauli_x, my_alpha))
print("Sin Formula=", np.sin(np.pi * my_alpha))
Expectation= 0.80901700258255 Sin Formula= 0.8090169943749475
এবং আপনি যদি \(f_{1}(\alpha) = ⟨Y(\alpha)| X | Y(\alpha)⟩\) সংজ্ঞায়িত করেন তাহলে \(f_{1}^{'}(\alpha) = \pi \cos(\pi \alpha)\)। আসুন এটি পরীক্ষা করা যাক:
def my_grad(obs, alpha, eps=0.01):
grad = 0
f_x = my_expectation(obs, alpha)
f_x_prime = my_expectation(obs, alpha + eps)
return ((f_x_prime - f_x) / eps).real
print('Finite difference:', my_grad(pauli_x, my_alpha))
print('Cosine formula: ', np.pi * np.cos(np.pi * my_alpha))
Finite difference: 1.8063604831695557 Cosine formula: 1.8465818304904567
2. একটি পার্থক্যকারীর প্রয়োজন
বৃহত্তর সার্কিটগুলির সাথে, আপনি সর্বদা এমন একটি সূত্র পাওয়ার জন্য এতটা ভাগ্যবান হবেন না যা একটি নির্দিষ্ট কোয়ান্টাম সার্কিটের গ্রেডিয়েন্টগুলি সঠিকভাবে গণনা করে। গ্রেডিয়েন্ট গণনা করার জন্য একটি সাধারণ সূত্র যথেষ্ট না হলে, tfq.differentiators.Differentiator ক্লাস আপনাকে আপনার সার্কিটের গ্রেডিয়েন্ট গণনার জন্য অ্যালগরিদম সংজ্ঞায়িত করতে দেয়। উদাহরণস্বরূপ আপনি টেনসরফ্লো কোয়ান্টাম (TFQ) এর সাথে উপরের উদাহরণটি পুনরায় তৈরি করতে পারেন:
expectation_calculation = tfq.layers.Expectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=[[my_alpha]])
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.80901706]], dtype=float32)>
যাইহোক, যদি আপনি স্যাম্পলিং (একটি সত্যিকারের ডিভাইসে কী ঘটবে) উপর ভিত্তি করে প্রত্যাশার অনুমানে স্যুইচ করেন তবে মানগুলি কিছুটা পরিবর্তন করতে পারে। এর মানে আপনার কাছে এখন একটি অপূর্ণ অনুমান আছে:
sampled_expectation_calculation = tfq.layers.SampledExpectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
sampled_expectation_calculation(my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=[[my_alpha]])
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.836]], dtype=float32)>
গ্রেডিয়েন্টের ক্ষেত্রে এটি দ্রুত একটি গুরুতর নির্ভুলতার সমস্যায় পরিণত হতে পারে:
# Make input_points = [batch_size, 1] array.
input_points = np.linspace(0, 5, 200)[:, np.newaxis].astype(np.float32)
exact_outputs = expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=input_points)
imperfect_outputs = sampled_expectation_calculation(my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=input_points)
plt.title('Forward Pass Values')
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.plot(input_points, exact_outputs, label='Analytic')
plt.plot(input_points, imperfect_outputs, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07d556190>
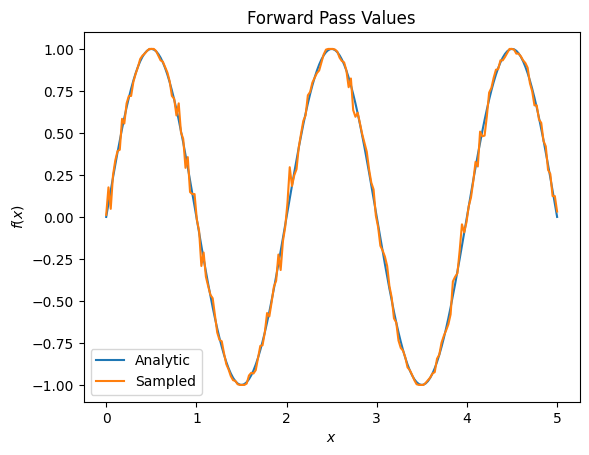
# Gradients are a much different story.
values_tensor = tf.convert_to_tensor(input_points)
with tf.GradientTape() as g:
g.watch(values_tensor)
exact_outputs = expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=values_tensor)
analytic_finite_diff_gradients = g.gradient(exact_outputs, values_tensor)
with tf.GradientTape() as g:
g.watch(values_tensor)
imperfect_outputs = sampled_expectation_calculation(
my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=values_tensor)
sampled_finite_diff_gradients = g.gradient(imperfect_outputs, values_tensor)
plt.title('Gradient Values')
plt.xlabel('$x$')
plt.ylabel('$f^{\'}(x)$')
plt.plot(input_points, analytic_finite_diff_gradients, label='Analytic')
plt.plot(input_points, sampled_finite_diff_gradients, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07adb8dd0>
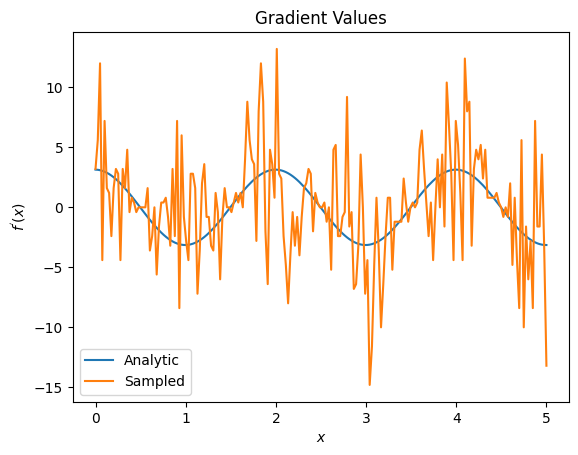
এখানে আপনি দেখতে পাচ্ছেন যে যদিও সীমিত পার্থক্য সূত্রটি বিশ্লেষণাত্মক ক্ষেত্রে গ্রেডিয়েন্টগুলিকে গণনা করার জন্য দ্রুত, যখন এটি নমুনা ভিত্তিক পদ্ধতিতে আসে তখন এটি খুব বেশি গোলমাল ছিল। একটি ভাল গ্রেডিয়েন্ট গণনা করা যায় তা নিশ্চিত করতে আরও সতর্ক কৌশল ব্যবহার করা আবশ্যক। এরপরে আপনি একটি অনেক ধীরগতির কৌশল দেখবেন যা বিশ্লেষণাত্মক প্রত্যাশা গ্রেডিয়েন্ট গণনার জন্য উপযুক্ত হবে না, তবে বাস্তব-বিশ্বের নমুনা ভিত্তিক ক্ষেত্রে অনেক ভালো কাজ করে:
# A smarter differentiation scheme.
gradient_safe_sampled_expectation = tfq.layers.SampledExpectation(
differentiator=tfq.differentiators.ParameterShift())
with tf.GradientTape() as g:
g.watch(values_tensor)
imperfect_outputs = gradient_safe_sampled_expectation(
my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=values_tensor)
sampled_param_shift_gradients = g.gradient(imperfect_outputs, values_tensor)
plt.title('Gradient Values')
plt.xlabel('$x$')
plt.ylabel('$f^{\'}(x)$')
plt.plot(input_points, analytic_finite_diff_gradients, label='Analytic')
plt.plot(input_points, sampled_param_shift_gradients, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07ad9ff90>
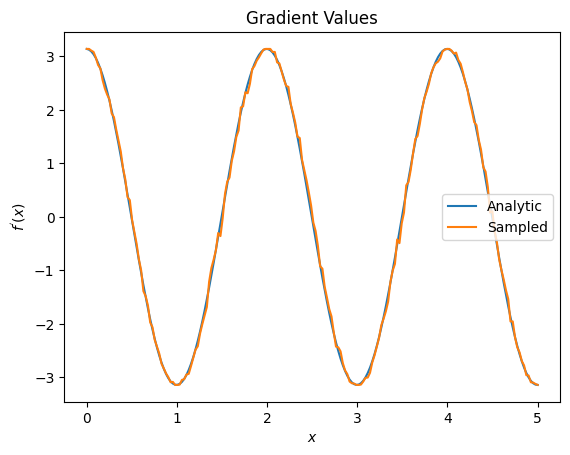
উপরের থেকে আপনি দেখতে পাচ্ছেন যে নির্দিষ্ট ডিফারেনশিয়াটরগুলি বিশেষ গবেষণার পরিস্থিতিতে সবচেয়ে ভাল ব্যবহার করা হয়। সাধারণভাবে, ধীরগতির নমুনা-ভিত্তিক পদ্ধতিগুলি যেগুলি ডিভাইসের শব্দের জন্য শক্তিশালী, ইত্যাদি, একটি আরও "বাস্তব বিশ্ব" সেটিংয়ে অ্যালগরিদম পরীক্ষা বা প্রয়োগ করার সময় দুর্দান্ত পার্থক্যকারী। সীমিত পার্থক্যের মতো দ্রুততর পদ্ধতিগুলি বিশ্লেষণাত্মক গণনার জন্য দুর্দান্ত এবং আপনি উচ্চতর থ্রুপুট চান, তবে আপনার অ্যালগরিদমের ডিভাইসের কার্যকারিতা নিয়ে এখনও উদ্বিগ্ন নন।
3. একাধিক পর্যবেক্ষণযোগ্য
আসুন একটি দ্বিতীয় পর্যবেক্ষণযোগ্য পরিচয় করিয়ে দেই এবং দেখুন কিভাবে টেনসরফ্লো কোয়ান্টাম একটি একক সার্কিটের জন্য একাধিক পর্যবেক্ষণযোগ্যকে সমর্থন করে।
pauli_z = cirq.Z(qubit)
pauli_z
cirq.Z(cirq.GridQubit(0, 0))
যদি এই পর্যবেক্ষণযোগ্যটি আগের মতো একই সার্কিটের সাথে ব্যবহার করা হয়, তাহলে আপনার কাছে \(f_{2}(\alpha) = ⟨Y(\alpha)| Z | Y(\alpha)⟩ = \cos(\pi \alpha)\) এবং \(f_{2}^{'}(\alpha) = -\pi \sin(\pi \alpha)\)আছে। একটি দ্রুত পরীক্ষা করুন:
test_value = 0.
print('Finite difference:', my_grad(pauli_z, test_value))
print('Sin formula: ', -np.pi * np.sin(np.pi * test_value))
Finite difference: -0.04934072494506836 Sin formula: -0.0
এটি একটি ম্যাচ (যথেষ্ট কাছাকাছি)।
এখন আপনি যদি \(g(\alpha) = f_{1}(\alpha) + f_{2}(\alpha)\) সংজ্ঞায়িত করেন তাহলে \(g'(\alpha) = f_{1}^{'}(\alpha) + f^{'}_{2}(\alpha)\)। একটি সার্কিটের সাথে ব্যবহার করার জন্য TensorFlow কোয়ান্টামে একাধিক পর্যবেক্ষণযোগ্য সংজ্ঞায়িত করা \(g\)তে আরও শর্ত যোগ করার সমতুল্য।
এর মানে হল যে একটি সার্কিটে একটি নির্দিষ্ট প্রতীকের গ্রেডিয়েন্ট সেই সার্কিটে প্রয়োগ করা সেই প্রতীকটির জন্য প্রতিটি পর্যবেক্ষণযোগ্য গ্রেডিয়েন্টের সমষ্টির সমান। এটি TensorFlow গ্রেডিয়েন্ট গ্রহণ এবং ব্যাকপ্রোপগেশনের সাথে সামঞ্জস্যপূর্ণ (যেখানে আপনি একটি নির্দিষ্ট প্রতীকের গ্রেডিয়েন্ট হিসাবে সমস্ত পর্যবেক্ষণযোগ্য গ্রেডিয়েন্টের যোগফল দেন)।
sum_of_outputs = tfq.layers.Expectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
sum_of_outputs(my_circuit,
operators=[pauli_x, pauli_z],
symbol_names=['alpha'],
symbol_values=[[test_value]])
<tf.Tensor: shape=(1, 2), dtype=float32, numpy=array([[1.9106855e-15, 1.0000000e+00]], dtype=float32)>
এখানে আপনি প্রথম এন্ট্রিটি হচ্ছে প্রত্যাশা wrt Pauli X, এবং দ্বিতীয়টি হচ্ছে প্রত্যাশা wrt Pauli Z. এখন আপনি যখন গ্রেডিয়েন্টটি নিবেন:
test_value_tensor = tf.convert_to_tensor([[test_value]])
with tf.GradientTape() as g:
g.watch(test_value_tensor)
outputs = sum_of_outputs(my_circuit,
operators=[pauli_x, pauli_z],
symbol_names=['alpha'],
symbol_values=test_value_tensor)
sum_of_gradients = g.gradient(outputs, test_value_tensor)
print(my_grad(pauli_x, test_value) + my_grad(pauli_z, test_value))
print(sum_of_gradients.numpy())
3.0917350202798843 [[3.0917213]]
এখানে আপনি যাচাই করেছেন যে প্রতিটি পর্যবেক্ষণযোগ্য গ্রেডিয়েন্টের যোগফল প্রকৃতপক্ষে \(\alpha\)এর গ্রেডিয়েন্ট। এই আচরণটি সমস্ত TensorFlow কোয়ান্টাম ডিফারেনশিয়াটর দ্বারা সমর্থিত এবং বাকি TensorFlow এর সাথে সামঞ্জস্যের ক্ষেত্রে একটি গুরুত্বপূর্ণ ভূমিকা পালন করে৷
4. উন্নত ব্যবহার
TensorFlow কোয়ান্টাম সাবক্লাস tfq.differentiators.Differentiator এর ভিতরে বিদ্যমান সমস্ত পার্থক্যকারী। একটি পার্থক্যকারী বাস্তবায়ন করতে, একজন ব্যবহারকারীকে অবশ্যই দুটি ইন্টারফেসের একটি বাস্তবায়ন করতে হবে। মান হল get_gradient_circuits বাস্তবায়ন করা, যা বেস ক্লাসকে বলে যে গ্রেডিয়েন্টের একটি অনুমান পেতে কোন সার্কিটগুলি পরিমাপ করতে হবে। বিকল্পভাবে, আপনি differentiate_analytic এবং differentiate_sampled ওভারলোড করতে পারেন; ক্লাস tfq.differentiators.Adjoint এই পথ নেয়।
নিম্নলিখিতটি একটি সার্কিটের গ্রেডিয়েন্ট বাস্তবায়নের জন্য TensorFlow কোয়ান্টাম ব্যবহার করে। আপনি প্যারামিটার স্থানান্তরের একটি ছোট উদাহরণ ব্যবহার করবেন।
আপনি উপরে সংজ্ঞায়িত সার্কিটটি স্মরণ করুন, \(|\alpha⟩ = Y^{\alpha}|0⟩\)। আগের মতো, আপনি \(X\) পর্যবেক্ষণযোগ্য, \(f(\alpha) = ⟨\alpha|X|\alpha⟩\)এর বিপরীতে এই সার্কিটের প্রত্যাশা মান হিসাবে একটি ফাংশন সংজ্ঞায়িত করতে পারেন। প্যারামিটার শিফট নিয়ম ব্যবহার করে, এই সার্কিটের জন্য, আপনি খুঁজে পেতে পারেন যে ডেরিভেটিভ
\[\frac{\partial}{\partial \alpha} f(\alpha) = \frac{\pi}{2} f\left(\alpha + \frac{1}{2}\right) - \frac{ \pi}{2} f\left(\alpha - \frac{1}{2}\right)\]
get_gradient_circuits ফাংশন এই ডেরিভেটিভের উপাদান প্রদান করে।
class MyDifferentiator(tfq.differentiators.Differentiator):
"""A Toy differentiator for <Y^alpha | X |Y^alpha>."""
def __init__(self):
pass
def get_gradient_circuits(self, programs, symbol_names, symbol_values):
"""Return circuits to compute gradients for given forward pass circuits.
Every gradient on a quantum computer can be computed via measurements
of transformed quantum circuits. Here, you implement a custom gradient
for a specific circuit. For a real differentiator, you will need to
implement this function in a more general way. See the differentiator
implementations in the TFQ library for examples.
"""
# The two terms in the derivative are the same circuit...
batch_programs = tf.stack([programs, programs], axis=1)
# ... with shifted parameter values.
shift = tf.constant(1/2)
forward = symbol_values + shift
backward = symbol_values - shift
batch_symbol_values = tf.stack([forward, backward], axis=1)
# Weights are the coefficients of the terms in the derivative.
num_program_copies = tf.shape(batch_programs)[0]
batch_weights = tf.tile(tf.constant([[[np.pi/2, -np.pi/2]]]),
[num_program_copies, 1, 1])
# The index map simply says which weights go with which circuits.
batch_mapper = tf.tile(
tf.constant([[[0, 1]]]), [num_program_copies, 1, 1])
return (batch_programs, symbol_names, batch_symbol_values,
batch_weights, batch_mapper)
Differentiator বেস ক্লাস ডেরিভেটিভ গণনা করতে get_gradient_circuits থেকে ফিরে আসা উপাদানগুলি ব্যবহার করে, যেমন আপনি উপরে দেখেছেন প্যারামিটার শিফট সূত্রে। এই নতুন পার্থক্যকারীটি এখন বিদ্যমান tfq.layer অবজেক্টের সাথে ব্যবহার করা যেতে পারে:
custom_dif = MyDifferentiator()
custom_grad_expectation = tfq.layers.Expectation(differentiator=custom_dif)
# Now let's get the gradients with finite diff.
with tf.GradientTape() as g:
g.watch(values_tensor)
exact_outputs = expectation_calculation(my_circuit,
operators=[pauli_x],
symbol_names=['alpha'],
symbol_values=values_tensor)
analytic_finite_diff_gradients = g.gradient(exact_outputs, values_tensor)
# Now let's get the gradients with custom diff.
with tf.GradientTape() as g:
g.watch(values_tensor)
my_outputs = custom_grad_expectation(my_circuit,
operators=[pauli_x],
symbol_names=['alpha'],
symbol_values=values_tensor)
my_gradients = g.gradient(my_outputs, values_tensor)
plt.subplot(1, 2, 1)
plt.title('Exact Gradient')
plt.plot(input_points, analytic_finite_diff_gradients.numpy())
plt.xlabel('x')
plt.ylabel('f(x)')
plt.subplot(1, 2, 2)
plt.title('My Gradient')
plt.plot(input_points, my_gradients.numpy())
plt.xlabel('x')
Text(0.5, 0, 'x')
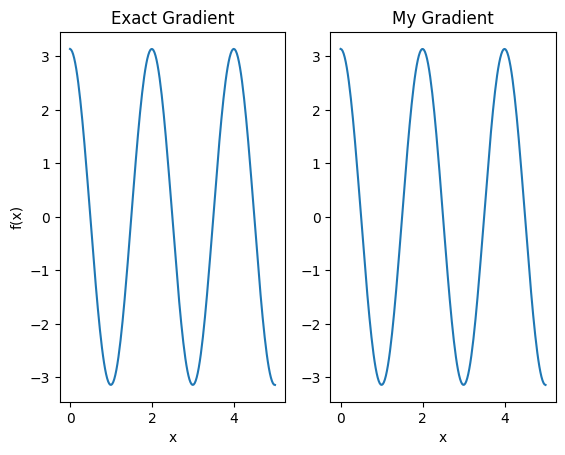
এই নতুন ডিফারেনশিয়াটরটি এখন ডিফারেনশিয়াবল অপ্স তৈরি করতে ব্যবহার করা যেতে পারে।
# Create a noisy sample based expectation op.
expectation_sampled = tfq.get_sampled_expectation_op(
cirq.DensityMatrixSimulator(noise=cirq.depolarize(0.01)))
# Make it differentiable with your differentiator:
# Remember to refresh the differentiator before attaching the new op
custom_dif.refresh()
differentiable_op = custom_dif.generate_differentiable_op(
sampled_op=expectation_sampled)
# Prep op inputs.
circuit_tensor = tfq.convert_to_tensor([my_circuit])
op_tensor = tfq.convert_to_tensor([[pauli_x]])
single_value = tf.convert_to_tensor([[my_alpha]])
num_samples_tensor = tf.convert_to_tensor([[5000]])
with tf.GradientTape() as g:
g.watch(single_value)
forward_output = differentiable_op(circuit_tensor, ['alpha'], single_value,
op_tensor, num_samples_tensor)
my_gradients = g.gradient(forward_output, single_value)
print('---TFQ---')
print('Foward: ', forward_output.numpy())
print('Gradient:', my_gradients.numpy())
print('---Original---')
print('Forward: ', my_expectation(pauli_x, my_alpha))
print('Gradient:', my_grad(pauli_x, my_alpha))
---TFQ--- Foward: [[0.8016]] Gradient: [[1.7932211]] ---Original--- Forward: 0.80901700258255 Gradient: 1.8063604831695557
