 TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
Bu örnekte, öğrenme söz konusu olduğunda yalnızca herhangi bir kuantum sinir ağı yapısının iyi olmayacağını söyleyen McClean, 2019'un sonucunu keşfedeceksiniz. Özellikle, belirli bir büyük rastgele kuantum devreleri ailesinin, neredeyse her yerde kaybolan gradyanlara sahip oldukları için iyi kuantum sinir ağları olarak hizmet etmediğini göreceksiniz. Bu örnekte, belirli bir öğrenme problemi için herhangi bir model eğitmeyecek, bunun yerine gradyanların davranışlarını anlamak gibi daha basit bir probleme odaklanacaksınız.
Kurmak
pip install tensorflow==2.7.0
TensorFlow Quantum'u yükleyin:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Şimdi TensorFlow ve modül bağımlılıklarını içe aktarın:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
np.random.seed(1234)
2022-02-04 12:15:43.355568: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Özet
Şuna benzeyen birçok blok içeren rastgele kuantum devreleri (\(R_{P}(\theta)\) , rastgele bir Pauli dönüşüdür):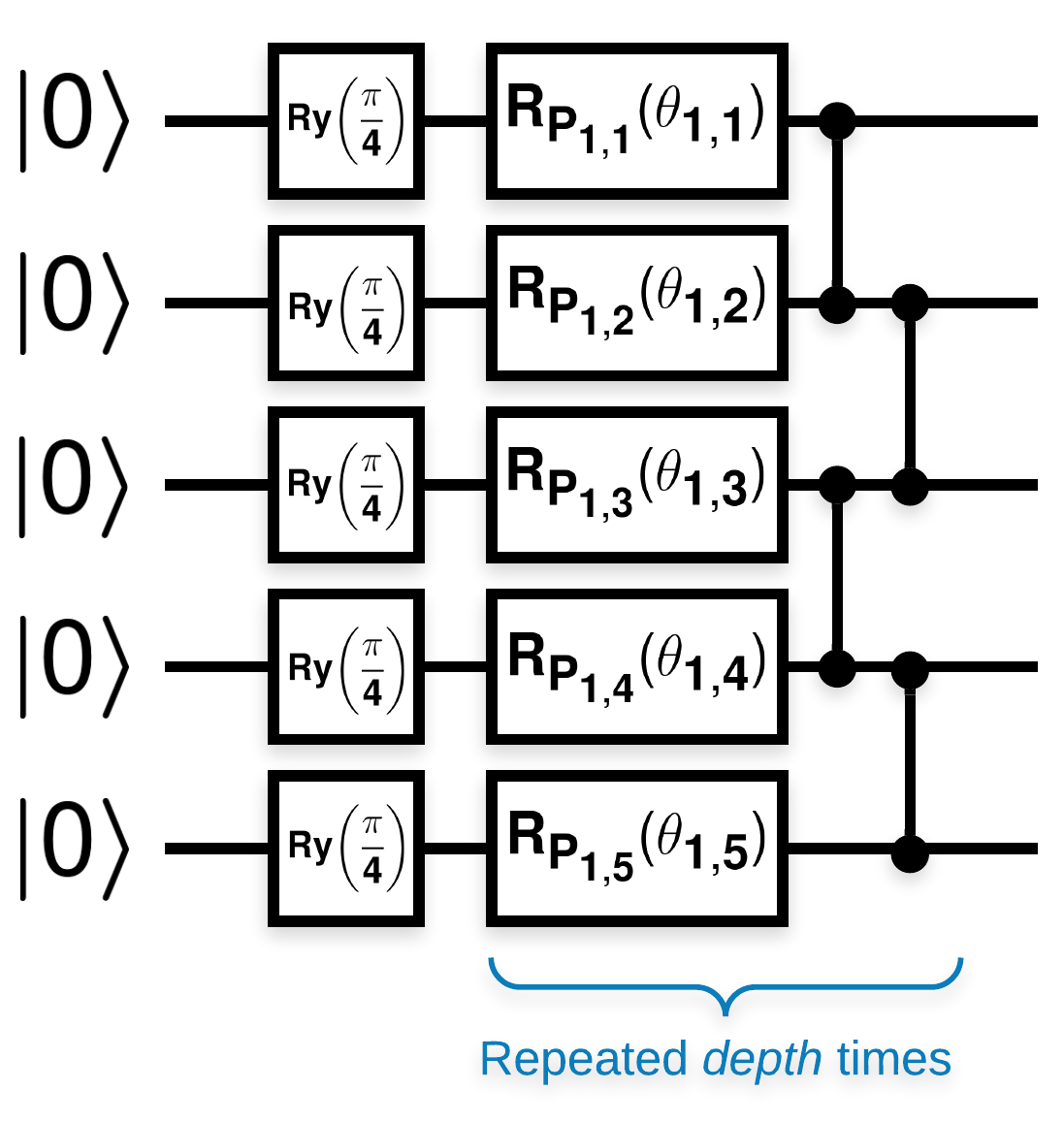
\(f(x)\) placeholder2, herhangi bir \(a\) ve \(b\)kübiti için wrt \(Z_{a}Z_{b}\) beklenti değeri olarak tanımlanırsa, \(f'(x)\) 0'a çok yakın bir ortalamaya sahip olması ve çok fazla değişmemesi gibi bir sorun vardır. Bunu aşağıda göreceksiniz:
2. Rastgele devreler oluşturma
Kağıttan yapılan yapıyı takip etmek kolaydır. Aşağıdakiler, bir dizi kubit üzerinde belirli bir derinlikle rastgele bir kuantum devresi (bazen bir kuantum sinir ağı (QNN) olarak anılır) oluşturan basit bir işlevi uygular:
def generate_random_qnn(qubits, symbol, depth):
"""Generate random QNN's with the same structure from McClean et al."""
circuit = cirq.Circuit()
for qubit in qubits:
circuit += cirq.ry(np.pi / 4.0)(qubit)
for d in range(depth):
# Add a series of single qubit rotations.
for i, qubit in enumerate(qubits):
random_n = np.random.uniform()
random_rot = np.random.uniform(
) * 2.0 * np.pi if i != 0 or d != 0 else symbol
if random_n > 2. / 3.:
# Add a Z.
circuit += cirq.rz(random_rot)(qubit)
elif random_n > 1. / 3.:
# Add a Y.
circuit += cirq.ry(random_rot)(qubit)
else:
# Add a X.
circuit += cirq.rx(random_rot)(qubit)
# Add CZ ladder.
for src, dest in zip(qubits, qubits[1:]):
circuit += cirq.CZ(src, dest)
return circuit
generate_random_qnn(cirq.GridQubit.rect(1, 3), sympy.Symbol('theta'), 2)
Yazarlar, tek bir parametre \(\theta_{1,1}\)gradyanını araştırıyor. \(\theta_{1,1}\) olacağı devreye bir sympy.Symbol koyarak devam edelim. Yazarlar devredeki diğer sembollerin istatistiklerini analiz etmediğinden, bunları daha sonra yerine şimdi rastgele değerlerle değiştirelim.
3. Devreleri Çalıştırmak
Gradyanların çok fazla değişmediği iddiasını test etmek için bir gözlemlenebilir ile birlikte bu devrelerden birkaçını oluşturun. İlk olarak, bir grup rastgele devre oluşturun. Rastgele bir gözlemlenebilir ZZ seçin ve TensorFlow Quantum'u kullanarak gradyanları ve varyansı toplu olarak hesaplayın.
3.1 Toplu varyans hesaplaması
Bir grup devre üzerinde verilen bir gözlemlenebilirin gradyanının varyansını hesaplayan bir yardımcı fonksiyon yazalım:
def process_batch(circuits, symbol, op):
"""Compute the variance of a batch of expectations w.r.t. op on each circuit that
contains `symbol`. Note that this method sets up a new compute graph every time it is
called so it isn't as performant as possible."""
# Setup a simple layer to batch compute the expectation gradients.
expectation = tfq.layers.Expectation()
# Prep the inputs as tensors
circuit_tensor = tfq.convert_to_tensor(circuits)
values_tensor = tf.convert_to_tensor(
np.random.uniform(0, 2 * np.pi, (n_circuits, 1)).astype(np.float32))
# Use TensorFlow GradientTape to track gradients.
with tf.GradientTape() as g:
g.watch(values_tensor)
forward = expectation(circuit_tensor,
operators=op,
symbol_names=[symbol],
symbol_values=values_tensor)
# Return variance of gradients across all circuits.
grads = g.gradient(forward, values_tensor)
grad_var = tf.math.reduce_std(grads, axis=0)
return grad_var.numpy()[0]
3.1 Kurulum ve çalıştırma
Derinlikleriyle birlikte oluşturulacak rastgele devrelerin sayısını ve üzerinde hareket etmeleri gereken kübit miktarını seçin. Ardından sonuçları çizin.
n_qubits = [2 * i for i in range(2, 7)
] # Ranges studied in paper are between 2 and 24.
depth = 50 # Ranges studied in paper are between 50 and 500.
n_circuits = 200
theta_var = []
for n in n_qubits:
# Generate the random circuits and observable for the given n.
qubits = cirq.GridQubit.rect(1, n)
symbol = sympy.Symbol('theta')
circuits = [
generate_random_qnn(qubits, symbol, depth) for _ in range(n_circuits)
]
op = cirq.Z(qubits[0]) * cirq.Z(qubits[1])
theta_var.append(process_batch(circuits, symbol, op))
plt.semilogy(n_qubits, theta_var)
plt.title('Gradient Variance in QNNs')
plt.xlabel('n_qubits')
plt.xticks(n_qubits)
plt.ylabel('$\\partial \\theta$ variance')
plt.show()
WARNING:tensorflow:5 out of the last 5 calls to <function Adjoint.differentiate_analytic at 0x7f9e3b5c68c0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details.
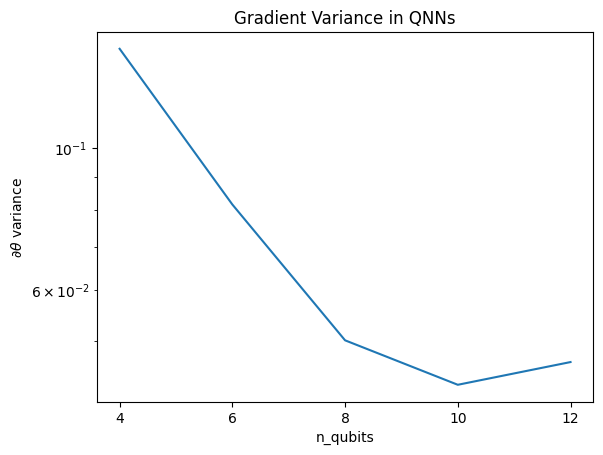
Bu çizim, kuantum makine öğrenme problemleri için rastgele bir QNN ansatzını tahmin edemeyeceğinizi ve en iyisini umamayacağınızı göstermektedir. Gradyanların öğrenmenin gerçekleşebileceği noktaya kadar değişebilmesi için model devresinde bazı yapıların mevcut olması gerekir.
4. Sezgisel
Grant'in ilginç bir buluşsal yöntemi olan 2019 , birinin rastgeleye çok yakın başlamasına izin verir, ancak tam olarak değil. Yazarlar, McClean ve diğerleri ile aynı devreleri kullanarak, çorak platolardan kaçınmak için klasik kontrol parametreleri için farklı bir başlatma tekniği önermektedir. Başlatma tekniği bazı katmanları tamamen rasgele kontrol parametreleriyle başlatır, ancak hemen takip eden katmanlarda, parametreleri ilk birkaç katman tarafından yapılan ilk dönüşümün geri alınacağı şekilde seçin. Yazarlar buna kimlik bloğu diyorlar.
Bu buluşsal yöntemin avantajı, yalnızca tek bir parametreyi değiştirerek, geçerli bloğun dışındaki tüm diğer blokların aynı kalması ve gradyan sinyalinin öncekinden çok daha güçlü gelmesidir. Bu, kullanıcının güçlü bir gradyan sinyali elde etmek için hangi değişkenlerin ve blokların değiştirileceğini seçmesini ve seçmesini sağlar. Bu buluşsal yöntem, kullanıcının eğitim aşamasında çorak bir platoya düşmesini engellemez (ve tamamen eşzamanlı bir güncellemeyi kısıtlar), sadece bir platonun dışında başlayabilmenizi garanti eder.
4.1 Yeni QNN yapısı
Şimdi kimlik bloğu QNN'leri oluşturmak için bir fonksiyon oluşturun. Bu uygulama, kağıttakinden biraz farklıdır. Şimdilik, McClean ve diğerleri ile tutarlı olması için tek bir parametrenin gradyanının davranışına bakın, böylece bazı basitleştirmeler yapılabilir.
Bir kimlik bloğu oluşturmak ve modeli eğitmek için, genellikle \(U1(\theta_{1a}) U1(\theta_{1b})^{\dagger}\) değil, \(U1(\theta_1) U1(\theta_1)^{\dagger}\)ihtiyacınız vardır. Başlangıçta \(\theta_{1a}\) ve \(\theta_{1b}\) aynı açılardır ancak bağımsız olarak öğrenilirler. Aksi takdirde, eğitimden sonra bile kimliği her zaman alırsınız. Kimlik bloklarının sayısı için seçim ampiriktir. Blok ne kadar derin olursa, bloğun ortasındaki varyans o kadar küçük olur. Ancak bloğun başında ve sonunda, parametre gradyanlarının varyansı büyük olmalıdır.
def generate_identity_qnn(qubits, symbol, block_depth, total_depth):
"""Generate random QNN's with the same structure from Grant et al."""
circuit = cirq.Circuit()
# Generate initial block with symbol.
prep_and_U = generate_random_qnn(qubits, symbol, block_depth)
circuit += prep_and_U
# Generate dagger of initial block without symbol.
U_dagger = (prep_and_U[1:])**-1
circuit += cirq.resolve_parameters(
U_dagger, param_resolver={symbol: np.random.uniform() * 2 * np.pi})
for d in range(total_depth - 1):
# Get a random QNN.
prep_and_U_circuit = generate_random_qnn(
qubits,
np.random.uniform() * 2 * np.pi, block_depth)
# Remove the state-prep component
U_circuit = prep_and_U_circuit[1:]
# Add U
circuit += U_circuit
# Add U^dagger
circuit += U_circuit**-1
return circuit
generate_identity_qnn(cirq.GridQubit.rect(1, 3), sympy.Symbol('theta'), 2, 2)
4.2 Karşılaştırma
Burada buluşsal yöntemin degradenin varyansının hızla kaybolmasını önlemeye yardımcı olduğunu görebilirsiniz:
block_depth = 10
total_depth = 5
heuristic_theta_var = []
for n in n_qubits:
# Generate the identity block circuits and observable for the given n.
qubits = cirq.GridQubit.rect(1, n)
symbol = sympy.Symbol('theta')
circuits = [
generate_identity_qnn(qubits, symbol, block_depth, total_depth)
for _ in range(n_circuits)
]
op = cirq.Z(qubits[0]) * cirq.Z(qubits[1])
heuristic_theta_var.append(process_batch(circuits, symbol, op))
plt.semilogy(n_qubits, theta_var)
plt.semilogy(n_qubits, heuristic_theta_var)
plt.title('Heuristic vs. Random')
plt.xlabel('n_qubits')
plt.xticks(n_qubits)
plt.ylabel('$\\partial \\theta$ variance')
plt.show()
WARNING:tensorflow:6 out of the last 6 calls to <function Adjoint.differentiate_analytic at 0x7f9e3b5c68c0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details.
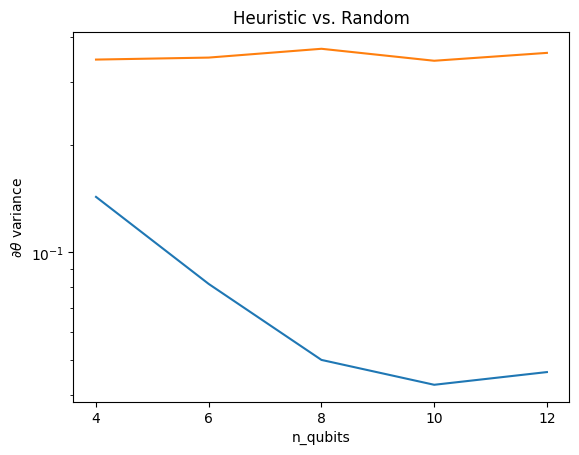
Bu, (yakın) rastgele QNN'lerden daha güçlü gradyan sinyalleri alma konusunda büyük bir gelişmedir.
