 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
W tym przykładzie przyjrzysz się wynikowi McClean, 2019, który mówi, że nie każda kwantowa struktura sieci neuronowej sprawdzi się dobrze, jeśli chodzi o uczenie się. W szczególności zobaczysz, że pewna duża rodzina losowych obwodów kwantowych nie służy jako dobre kwantowe sieci neuronowe, ponieważ mają gradienty, które znikają prawie wszędzie. W tym przykładzie nie będziesz trenował żadnych modeli dla konkretnego problemu uczenia się, ale zamiast tego skupisz się na prostszym problemie zrozumienia zachowań gradientów.
Ustawiać
pip install tensorflow==2.7.0
Zainstaluj TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Teraz zaimportuj TensorFlow i zależności modułu:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
np.random.seed(1234)
2022-02-04 12:15:43.355568: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Podsumowanie
Losowe obwody kwantowe z wieloma blokami, które wyglądają tak (\(R_{P}(\theta)\) to losowa rotacja Pauliego):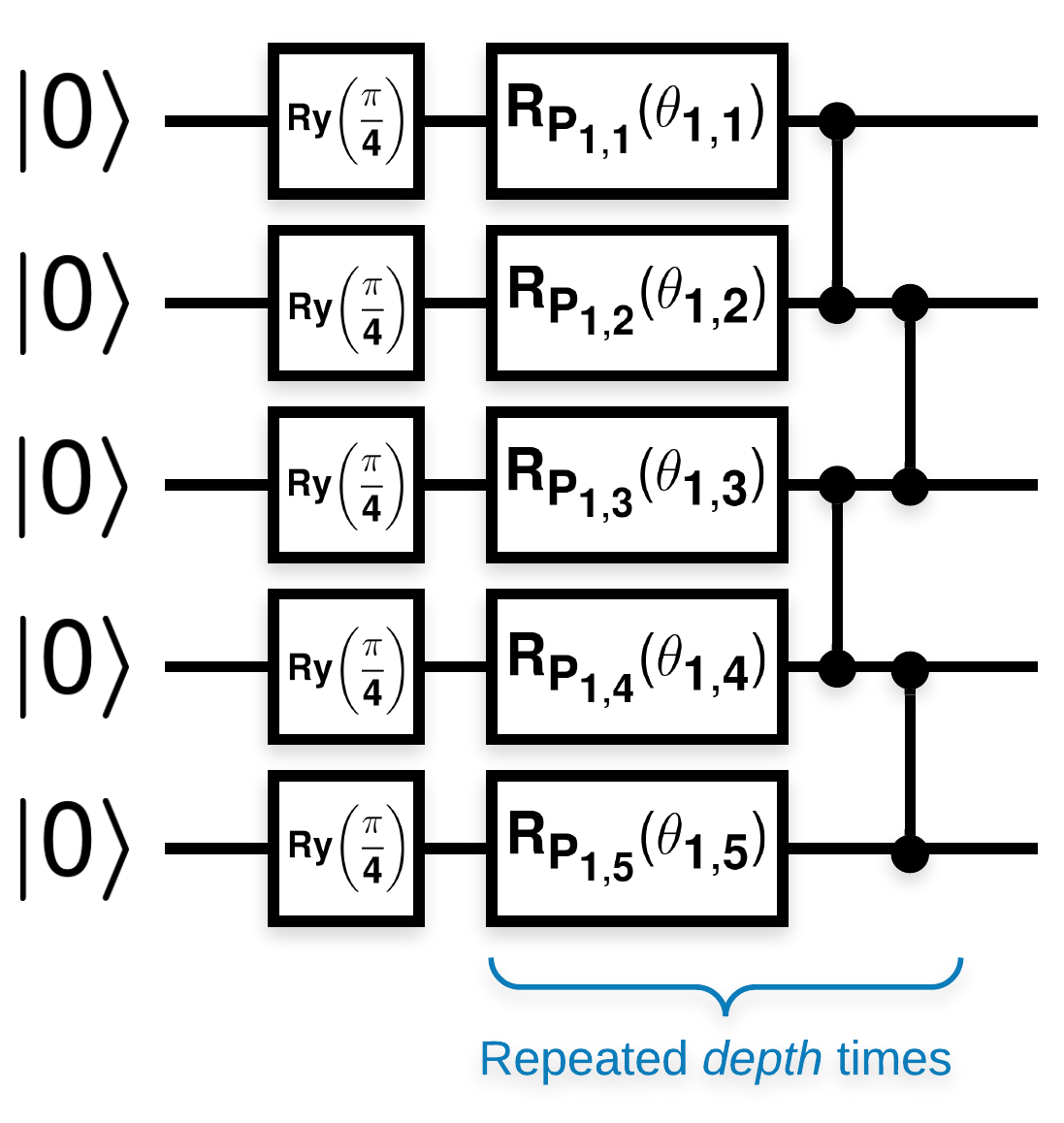
Gdzie, jeśli \(f(x)\) jest zdefiniowany jako wartość oczekiwana wrt \(Z_{a}Z_{b}\) dla dowolnych kubitów \(a\) i \(b\), wówczas występuje problem polegający na tym, że \(f'(x)\) ma średnią bardzo bliską 0 i niewiele się różni. Zobaczysz to poniżej:
2. Generowanie losowych obwodów
Konstrukcja z papieru jest łatwa do naśladowania. Poniżej zaimplementowano prostą funkcję, która generuje losowy obwód kwantowy — czasami nazywany kwantową siecią neuronową (QNN) — o określonej głębokości na zestawie kubitów:
def generate_random_qnn(qubits, symbol, depth):
"""Generate random QNN's with the same structure from McClean et al."""
circuit = cirq.Circuit()
for qubit in qubits:
circuit += cirq.ry(np.pi / 4.0)(qubit)
for d in range(depth):
# Add a series of single qubit rotations.
for i, qubit in enumerate(qubits):
random_n = np.random.uniform()
random_rot = np.random.uniform(
) * 2.0 * np.pi if i != 0 or d != 0 else symbol
if random_n > 2. / 3.:
# Add a Z.
circuit += cirq.rz(random_rot)(qubit)
elif random_n > 1. / 3.:
# Add a Y.
circuit += cirq.ry(random_rot)(qubit)
else:
# Add a X.
circuit += cirq.rx(random_rot)(qubit)
# Add CZ ladder.
for src, dest in zip(qubits, qubits[1:]):
circuit += cirq.CZ(src, dest)
return circuit
generate_random_qnn(cirq.GridQubit.rect(1, 3), sympy.Symbol('theta'), 2)
Autorzy badają gradient pojedynczego parametru \(\theta_{1,1}\). Przejdźmy dalej, umieszczając sympy.Symbol w obwodzie w miejscu, w którym byłby \(\theta_{1,1}\) . Ponieważ autorzy nie analizują statystyk dla żadnych innych symboli w obwodzie, zastąpmy je wartościami losowymi teraz, a nie później.
3. Uruchamianie obwodów
Wygeneruj kilka z tych obwodów wraz z obserwowalnym, aby przetestować twierdzenie, że gradienty nie różnią się zbytnio. Najpierw wygeneruj partię losowych obwodów. Wybierz losowy obserwowalny ZZ i oblicz wsadowo gradienty i wariancję za pomocą TensorFlow Quantum.
3.1 Obliczanie wariancji wsadowej
Napiszmy funkcję pomocniczą, która oblicza wariancję gradientu danej obserwowalnej na partii obwodów:
def process_batch(circuits, symbol, op):
"""Compute the variance of a batch of expectations w.r.t. op on each circuit that
contains `symbol`. Note that this method sets up a new compute graph every time it is
called so it isn't as performant as possible."""
# Setup a simple layer to batch compute the expectation gradients.
expectation = tfq.layers.Expectation()
# Prep the inputs as tensors
circuit_tensor = tfq.convert_to_tensor(circuits)
values_tensor = tf.convert_to_tensor(
np.random.uniform(0, 2 * np.pi, (n_circuits, 1)).astype(np.float32))
# Use TensorFlow GradientTape to track gradients.
with tf.GradientTape() as g:
g.watch(values_tensor)
forward = expectation(circuit_tensor,
operators=op,
symbol_names=[symbol],
symbol_values=values_tensor)
# Return variance of gradients across all circuits.
grads = g.gradient(forward, values_tensor)
grad_var = tf.math.reduce_std(grads, axis=0)
return grad_var.numpy()[0]
3.1 Konfiguracja i uruchomienie
Wybierz liczbę losowych obwodów do wygenerowania wraz z ich głębokością i liczbą kubitów, na których mają działać. Następnie wykreśl wyniki.
n_qubits = [2 * i for i in range(2, 7)
] # Ranges studied in paper are between 2 and 24.
depth = 50 # Ranges studied in paper are between 50 and 500.
n_circuits = 200
theta_var = []
for n in n_qubits:
# Generate the random circuits and observable for the given n.
qubits = cirq.GridQubit.rect(1, n)
symbol = sympy.Symbol('theta')
circuits = [
generate_random_qnn(qubits, symbol, depth) for _ in range(n_circuits)
]
op = cirq.Z(qubits[0]) * cirq.Z(qubits[1])
theta_var.append(process_batch(circuits, symbol, op))
plt.semilogy(n_qubits, theta_var)
plt.title('Gradient Variance in QNNs')
plt.xlabel('n_qubits')
plt.xticks(n_qubits)
plt.ylabel('$\\partial \\theta$ variance')
plt.show()
WARNING:tensorflow:5 out of the last 5 calls to <function Adjoint.differentiate_analytic at 0x7f9e3b5c68c0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details.
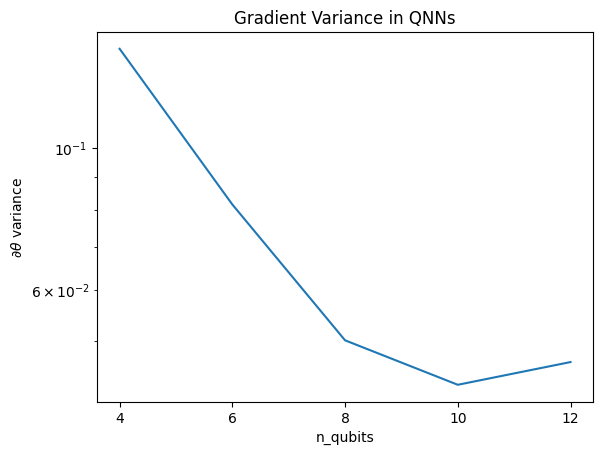
Ten wykres pokazuje, że w przypadku problemów z uczeniem maszyn kwantowych nie można po prostu odgadnąć losowego odpowiedzi QNN i mieć nadzieję na najlepsze. W obwodzie modelu musi być obecna pewna struktura, aby gradienty zmieniały się do punktu, w którym może nastąpić uczenie się.
4. Heurystyka
Ciekawa heurystyka Grant, 2019 pozwala zacząć bardzo blisko losowości, ale nie do końca. Wykorzystując te same obwody, co McClean i in., autorzy proponują inną technikę inicjalizacji klasycznych parametrów kontrolnych, aby uniknąć jałowych płaskowyżów. Technika inicjalizacji uruchamia niektóre warstwy z całkowicie losowymi parametrami kontrolnymi — ale w warstwach bezpośrednio następujących należy wybrać takie parametry, aby początkowa transformacja dokonana przez kilka pierwszych warstw została cofnięta. Autorzy nazywają to blokiem tożsamości .
Zaletą tej heurystyki jest to, że zmieniając tylko jeden parametr, wszystkie inne bloki poza bieżącym blokiem pozostaną identyczne — a sygnał gradientu przechodzi przez znacznie silniejszy niż wcześniej. Pozwala to użytkownikowi wybrać i wybrać zmienne i bloki do zmodyfikowania w celu uzyskania silnego sygnału gradientowego. Ta heurystyka nie chroni użytkownika przed upadkiem na jałowy płaskowyż podczas fazy treningu (i ogranicza w pełni jednoczesną aktualizację), po prostu gwarantuje, że możesz zacząć poza płaskowyżem.
4.1 Nowa konstrukcja QNN
Teraz skonstruuj funkcję generującą bloki tożsamości QNN. Ta implementacja jest nieco inna niż ta z papieru. Na razie spójrz na zachowanie gradientu pojedynczego parametru, aby było zgodne z McCleanem i in., aby można było dokonać pewnych uproszczeń.
Aby wygenerować blok tożsamości i wytrenować model, zazwyczaj potrzebujesz \(U1(\theta_{1a}) U1(\theta_{1b})^{\dagger}\) , a nie \(U1(\theta_1) U1(\theta_1)^{\dagger}\). Początkowo \(\theta_{1a}\) i \(\theta_{1b}\) są tymi samymi kątami, ale uczy się ich niezależnie. W przeciwnym razie tożsamość otrzymasz zawsze, nawet po treningu. Wybór liczby bloków tożsamości jest empiryczny. Im głębszy blok, tym mniejsza wariancja w środku bloku. Ale na początku i na końcu bloku wariancja gradientów parametrów powinna być duża.
def generate_identity_qnn(qubits, symbol, block_depth, total_depth):
"""Generate random QNN's with the same structure from Grant et al."""
circuit = cirq.Circuit()
# Generate initial block with symbol.
prep_and_U = generate_random_qnn(qubits, symbol, block_depth)
circuit += prep_and_U
# Generate dagger of initial block without symbol.
U_dagger = (prep_and_U[1:])**-1
circuit += cirq.resolve_parameters(
U_dagger, param_resolver={symbol: np.random.uniform() * 2 * np.pi})
for d in range(total_depth - 1):
# Get a random QNN.
prep_and_U_circuit = generate_random_qnn(
qubits,
np.random.uniform() * 2 * np.pi, block_depth)
# Remove the state-prep component
U_circuit = prep_and_U_circuit[1:]
# Add U
circuit += U_circuit
# Add U^dagger
circuit += U_circuit**-1
return circuit
generate_identity_qnn(cirq.GridQubit.rect(1, 3), sympy.Symbol('theta'), 2, 2)
4.2 Porównanie
Tutaj możesz zobaczyć, że heurystyka pomaga zapobiegać tak szybkiemu zanikaniu wariancji gradientu:
block_depth = 10
total_depth = 5
heuristic_theta_var = []
for n in n_qubits:
# Generate the identity block circuits and observable for the given n.
qubits = cirq.GridQubit.rect(1, n)
symbol = sympy.Symbol('theta')
circuits = [
generate_identity_qnn(qubits, symbol, block_depth, total_depth)
for _ in range(n_circuits)
]
op = cirq.Z(qubits[0]) * cirq.Z(qubits[1])
heuristic_theta_var.append(process_batch(circuits, symbol, op))
plt.semilogy(n_qubits, theta_var)
plt.semilogy(n_qubits, heuristic_theta_var)
plt.title('Heuristic vs. Random')
plt.xlabel('n_qubits')
plt.xticks(n_qubits)
plt.ylabel('$\\partial \\theta$ variance')
plt.show()
WARNING:tensorflow:6 out of the last 6 calls to <function Adjoint.differentiate_analytic at 0x7f9e3b5c68c0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details.
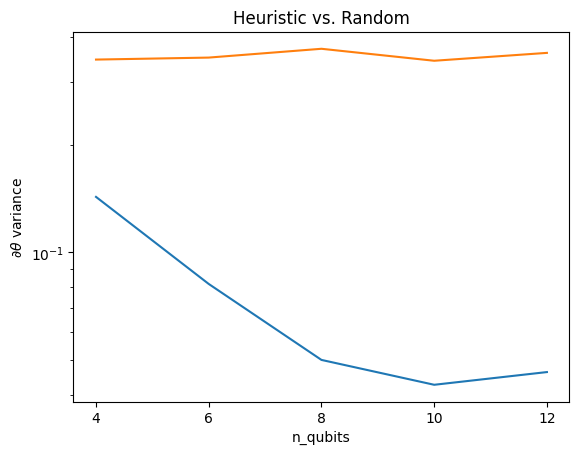
Jest to wielka poprawa w uzyskiwaniu silniejszych sygnałów gradientu z (prawie) losowych QNN.
