 TensorFlow.orgで表示 TensorFlow.orgで表示 |  GoogleColabで実行 GoogleColabで実行 |  GitHubでソースを表示 GitHubでソースを表示 |  ノートブックをダウンロード ノートブックをダウンロード |
この例では、学習に関しては、量子ニューラルネットワーク構造だけでうまくいくわけではないというMcClean、2019年の結果を探ります。特に、ランダム量子回路の特定の大きなファミリーは、ほとんどどこでも消える勾配を持っているため、優れた量子ニューラルネットワークとして機能しないことがわかります。この例では、特定の学習問題のモデルをトレーニングするのではなく、勾配の動作を理解するというより単純な問題に焦点を当てます。
設定
pip install tensorflow==2.7.0
TensorFlowQuantumをインストールします。
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>プレースホルダー16
次に、TensorFlowとモジュールの依存関係をインポートします。
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
np.random.seed(1234)
2022-02-04 12:15:43.355568: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detectedプレースホルダー18
1.まとめ
このように見える多くのブロックを持つランダム量子回路(\(R_{P}(\theta)\) はランダムなPauli回転です):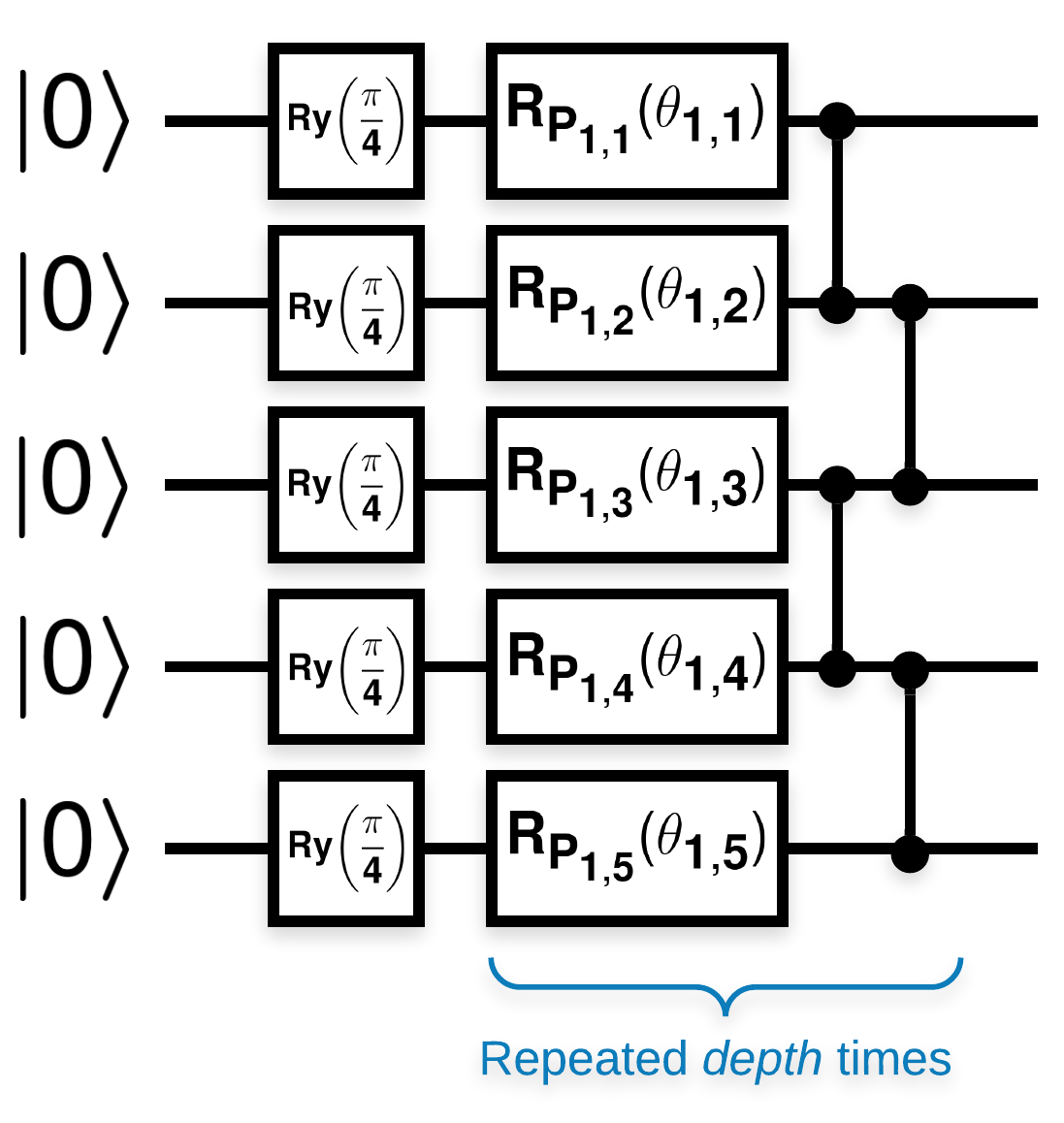
\(Z_{a}Z_{b}\) が任意のキュービット \(a\) および \(b\)の期待値wrtl10n-placeholder3として定義されている場合、 \(f(x)\) \(f'(x)\) の平均が0に非常に近く、あまり変化しないという問題があります。以下にこれが表示されます。
2.ランダム回路の生成
論文からの構成は簡単に理解できます。以下は、量子ビットのセットに指定された深さを持つランダム量子回路(量子ニューラルネットワーク(QNN)と呼ばれることもあります)を生成する単純な関数を実装しています。
def generate_random_qnn(qubits, symbol, depth):
"""Generate random QNN's with the same structure from McClean et al."""
circuit = cirq.Circuit()
for qubit in qubits:
circuit += cirq.ry(np.pi / 4.0)(qubit)
for d in range(depth):
# Add a series of single qubit rotations.
for i, qubit in enumerate(qubits):
random_n = np.random.uniform()
random_rot = np.random.uniform(
) * 2.0 * np.pi if i != 0 or d != 0 else symbol
if random_n > 2. / 3.:
# Add a Z.
circuit += cirq.rz(random_rot)(qubit)
elif random_n > 1. / 3.:
# Add a Y.
circuit += cirq.ry(random_rot)(qubit)
else:
# Add a X.
circuit += cirq.rx(random_rot)(qubit)
# Add CZ ladder.
for src, dest in zip(qubits, qubits[1:]):
circuit += cirq.CZ(src, dest)
return circuit
generate_random_qnn(cirq.GridQubit.rect(1, 3), sympy.Symbol('theta'), 2)
著者は、単一のパラメーター \(\theta_{1,1}\)の勾配を調査します。次に、 \(\theta_{1,1}\) がある回路にsympy.Symbolを配置します。著者は回路内の他のシンボルの統計を分析しないので、後でではなく今すぐランダムな値に置き換えましょう。
3.回路の実行
勾配があまり変化しないという主張をテストするために、オブザーバブルとともにこれらの回路のいくつかを生成します。まず、ランダム回路のバッチを生成します。観測可能なランダムなZZを選択し、TensorFlowQuantumを使用して勾配と分散をバッチ計算します。
3.1バッチ分散計算
回路のバッチ全体で観測可能な特定の勾配の分散を計算するヘルパー関数を作成してみましょう。
def process_batch(circuits, symbol, op):
"""Compute the variance of a batch of expectations w.r.t. op on each circuit that
contains `symbol`. Note that this method sets up a new compute graph every time it is
called so it isn't as performant as possible."""
# Setup a simple layer to batch compute the expectation gradients.
expectation = tfq.layers.Expectation()
# Prep the inputs as tensors
circuit_tensor = tfq.convert_to_tensor(circuits)
values_tensor = tf.convert_to_tensor(
np.random.uniform(0, 2 * np.pi, (n_circuits, 1)).astype(np.float32))
# Use TensorFlow GradientTape to track gradients.
with tf.GradientTape() as g:
g.watch(values_tensor)
forward = expectation(circuit_tensor,
operators=op,
symbol_names=[symbol],
symbol_values=values_tensor)
# Return variance of gradients across all circuits.
grads = g.gradient(forward, values_tensor)
grad_var = tf.math.reduce_std(grads, axis=0)
return grad_var.numpy()[0]
3.1セットアップと実行
生成するランダム回路の数と、それらが作用する必要のあるキュービットの深さを選択します。次に、結果をプロットします。
n_qubits = [2 * i for i in range(2, 7)
] # Ranges studied in paper are between 2 and 24.
depth = 50 # Ranges studied in paper are between 50 and 500.
n_circuits = 200
theta_var = []
for n in n_qubits:
# Generate the random circuits and observable for the given n.
qubits = cirq.GridQubit.rect(1, n)
symbol = sympy.Symbol('theta')
circuits = [
generate_random_qnn(qubits, symbol, depth) for _ in range(n_circuits)
]
op = cirq.Z(qubits[0]) * cirq.Z(qubits[1])
theta_var.append(process_batch(circuits, symbol, op))
plt.semilogy(n_qubits, theta_var)
plt.title('Gradient Variance in QNNs')
plt.xlabel('n_qubits')
plt.xticks(n_qubits)
plt.ylabel('$\\partial \\theta$ variance')
plt.show()
WARNING:tensorflow:5 out of the last 5 calls to <function Adjoint.differentiate_analytic at 0x7f9e3b5c68c0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details.
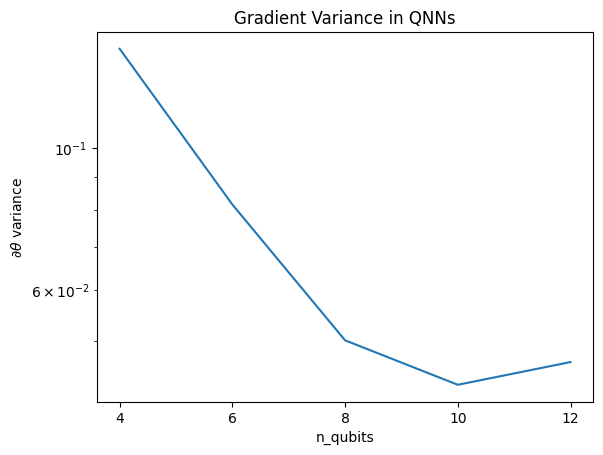
このプロットは、量子機械学習の問題について、ランダムなQNN仮説を単純に推測して、最良のものを期待することはできないことを示しています。勾配が学習が発生する可能性のあるポイントまで変化するためには、モデル回路に何らかの構造が存在する必要があります。
4.ヒューリスティック
Grantによる興味深いヒューリスティック、2019年では、ランダムに非常に近い状態で開始できますが、完全ではありません。 McClean et al。と同じ回路を使用して、著者は、不毛のプラトーを回避するために、古典的な制御パラメータに対して異なる初期化手法を提案しています。初期化手法は、完全にランダムな制御パラメーターを使用して一部のレイヤーを開始しますが、直後のレイヤーでは、最初のいくつかのレイヤーによって行われた最初の変換が取り消されるようにパラメーターを選択します。著者はこれをアイデンティティブロックと呼んでいます。
このヒューリスティックの利点は、1つのパラメーターを変更するだけで、現在のブロックの外側にある他のすべてのブロックがIDのままになり、勾配信号が以前よりもはるかに強力に通過することです。これにより、ユーザーは、強い勾配信号を取得するために変更する変数とブロックを選択できます。このヒューリスティックは、トレーニングフェーズ中にユーザーが不毛の高原に陥るのを防ぐことはなく(完全に同時更新を制限します)、高原の外から開始できることを保証するだけです。
4.1新しいQNNの構築
次に、IDブロックQNNを生成する関数を作成します。この実装は、論文の実装とは少し異なります。今のところ、単一のパラメーターの勾配の動作を見て、McClean et alと一致するようにして、いくつかの簡略化を行うことができます。
IDブロックを生成してモデルをトレーニングするには、通常、 \(U1(\theta_{1a}) U1(\theta_{1b})^{\dagger}\) ではなく \(U1(\theta_1) U1(\theta_1)^{\dagger}\)placeholder9が必要です。最初は、 \(\theta_{1a}\) と \(\theta_{1b}\) は同じ角度ですが、独立して学習されます。そうしないと、トレーニング後も常にIDを取得できます。 IDブロックの数の選択は経験に基づいています。ブロックが深いほど、ブロックの中央の分散は小さくなります。ただし、ブロックの開始時と終了時では、パラメーター勾配の分散を大きくする必要があります。
def generate_identity_qnn(qubits, symbol, block_depth, total_depth):
"""Generate random QNN's with the same structure from Grant et al."""
circuit = cirq.Circuit()
# Generate initial block with symbol.
prep_and_U = generate_random_qnn(qubits, symbol, block_depth)
circuit += prep_and_U
# Generate dagger of initial block without symbol.
U_dagger = (prep_and_U[1:])**-1
circuit += cirq.resolve_parameters(
U_dagger, param_resolver={symbol: np.random.uniform() * 2 * np.pi})
for d in range(total_depth - 1):
# Get a random QNN.
prep_and_U_circuit = generate_random_qnn(
qubits,
np.random.uniform() * 2 * np.pi, block_depth)
# Remove the state-prep component
U_circuit = prep_and_U_circuit[1:]
# Add U
circuit += U_circuit
# Add U^dagger
circuit += U_circuit**-1
return circuit
generate_identity_qnn(cirq.GridQubit.rect(1, 3), sympy.Symbol('theta'), 2, 2)
4.2比較
ここで、ヒューリスティックが勾配の分散がすぐに消えないようにするのに役立つことがわかります。
block_depth = 10
total_depth = 5
heuristic_theta_var = []
for n in n_qubits:
# Generate the identity block circuits and observable for the given n.
qubits = cirq.GridQubit.rect(1, n)
symbol = sympy.Symbol('theta')
circuits = [
generate_identity_qnn(qubits, symbol, block_depth, total_depth)
for _ in range(n_circuits)
]
op = cirq.Z(qubits[0]) * cirq.Z(qubits[1])
heuristic_theta_var.append(process_batch(circuits, symbol, op))
plt.semilogy(n_qubits, theta_var)
plt.semilogy(n_qubits, heuristic_theta_var)
plt.title('Heuristic vs. Random')
plt.xlabel('n_qubits')
plt.xticks(n_qubits)
plt.ylabel('$\\partial \\theta$ variance')
plt.show()
WARNING:tensorflow:6 out of the last 6 calls to <function Adjoint.differentiate_analytic at 0x7f9e3b5c68c0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details.
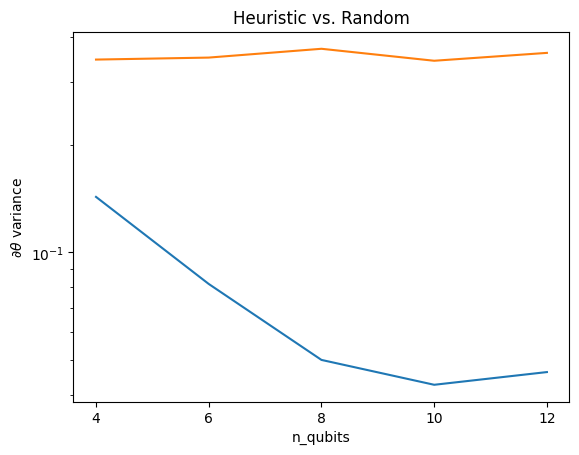
これは、(近くの)ランダムQNNからより強い勾配信号を取得する上での大きな改善です。
