TensorFlow در 14 مه به Google I/O بازگشته است! همین الان ثبت نام کنید

این صفحه به‌وسیله ‏Cloud Translation API‏ ترجمه شده است.

فلات های بایر

مشاهده در TensorFlow.org

در Google Colab اجرا شود

مشاهده منبع در GitHub

دانلود دفترچه یادداشت

در این مثال، شما نتیجه مک‌کلین، 2019 را بررسی می‌کنید که می‌گوید هر ساختار شبکه عصبی کوانتومی در یادگیری خوب عمل نمی‌کند. به طور خاص خواهید دید که یک خانواده بزرگ خاص از مدارهای کوانتومی تصادفی به عنوان شبکه های عصبی کوانتومی خوب عمل نمی کنند، زیرا آنها دارای گرادیان هایی هستند که تقریباً در همه جا ناپدید می شوند. در این مثال شما هیچ مدلی را برای یک مشکل یادگیری خاص آموزش نخواهید داد، بلکه در عوض بر روی مسئله ساده‌تر درک رفتارهای گرادیان تمرکز خواهید کرد.

برپایی

pip install tensorflow==2.7.0

TensorFlow Quantum را نصب کنید:

pip install tensorflow-quantum

# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)

<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>

اکنون TensorFlow و وابستگی های ماژول را وارد کنید:

import tensorflow as tf
import tensorflow_quantum as tfq

import cirq
import sympy
import numpy as np

# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit

np.random.seed(1234)

2022-02-04 12:15:43.355568: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected

1. خلاصه

مدارهای کوانتومی تصادفی با بلوک های زیادی که شبیه این هستند (\(R_{P}(\theta)\) یک چرخش تصادفی پائولی است):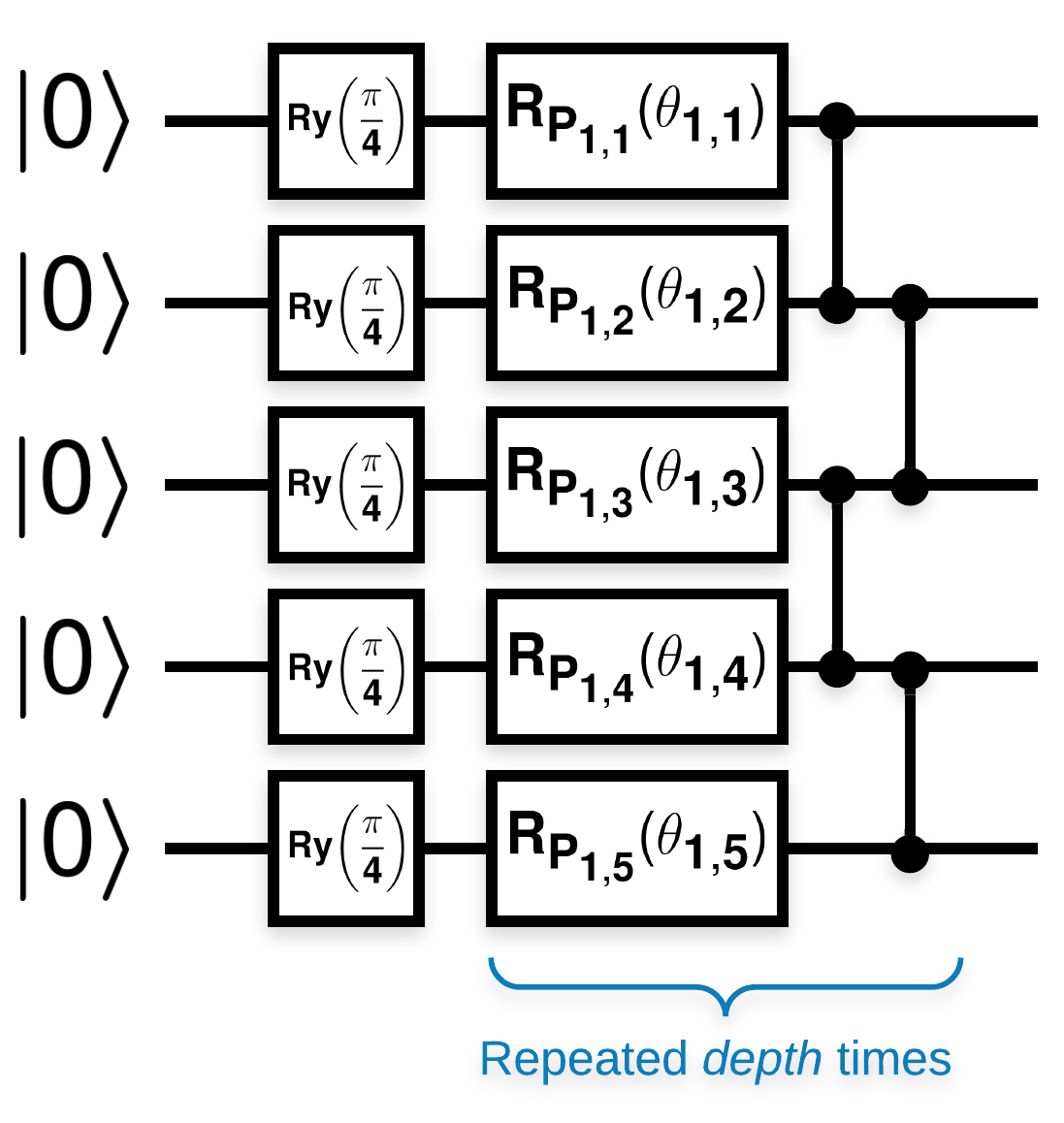

اگر \(f(x)\) به عنوان مقدار انتظار wrt \(Z_{a}Z_{b}\) برای هر کیوبیت \(a\) و \(b\)تعریف شود، مشکلی وجود دارد که \(f'(x)\) بسیار نزدیک به 0 دارد و تفاوت زیادی ندارد. این را در زیر خواهید دید:

2. تولید مدارهای تصادفی

ساخت و ساز از کاغذ ساده به دنبال است. زیر یک تابع ساده را پیاده سازی می کند که یک مدار کوانتومی تصادفی را ایجاد می کند - که گاهی اوقات به عنوان یک شبکه عصبی کوانتومی (QNN) شناخته می شود - با عمق داده شده در مجموعه ای از کیوبیت ها:

def generate_random_qnn(qubits, symbol, depth):
    """Generate random QNN's with the same structure from McClean et al."""
    circuit = cirq.Circuit()
    for qubit in qubits:
        circuit += cirq.ry(np.pi / 4.0)(qubit)

    for d in range(depth):
        # Add a series of single qubit rotations.
        for i, qubit in enumerate(qubits):
            random_n = np.random.uniform()
            random_rot = np.random.uniform(
            ) * 2.0 * np.pi if i != 0 or d != 0 else symbol
            if random_n > 2. / 3.:
                # Add a Z.
                circuit += cirq.rz(random_rot)(qubit)
            elif random_n > 1. / 3.:
                # Add a Y.
                circuit += cirq.ry(random_rot)(qubit)
            else:
                # Add a X.
                circuit += cirq.rx(random_rot)(qubit)

        # Add CZ ladder.
        for src, dest in zip(qubits, qubits[1:]):
            circuit += cirq.CZ(src, dest)

    return circuit


generate_random_qnn(cirq.GridQubit.rect(1, 3), sympy.Symbol('theta'), 2)

نویسندگان گرادیان یک پارامتر منفرد \(\theta_{1,1}\)بررسی می کنند. بیایید با قرار دادن یک sympy.Symbol در مداری که \(\theta_{1,1}\) قرار دارد، دنبال کنیم. از آنجایی که نویسندگان آمار هیچ نماد دیگری را در مدار تجزیه و تحلیل نمی کنند، بیایید به جای بعد، اکنون آنها را با مقادیر تصادفی جایگزین کنیم.

3. اجرای مدارها

تعدادی از این مدارها را به همراه یک مدار قابل مشاهده برای آزمایش این ادعا که گرادیان ها زیاد متفاوت نیستند، تولید کنید. ابتدا دسته ای از مدارهای تصادفی تولید کنید. یک ZZ قابل مشاهده تصادفی را انتخاب کنید و به صورت دسته ای گرادیان ها و واریانس ها را با استفاده از TensorFlow Quantum محاسبه کنید.

3.1 محاسبه واریانس دسته ای

بیایید یک تابع کمکی بنویسیم که واریانس گرادیان یک قابل مشاهده معین را روی دسته ای از مدارها محاسبه می کند:

def process_batch(circuits, symbol, op):
    """Compute the variance of a batch of expectations w.r.t. op on each circuit that 
    contains `symbol`. Note that this method sets up a new compute graph every time it is
    called so it isn't as performant as possible."""

    # Setup a simple layer to batch compute the expectation gradients.
    expectation = tfq.layers.Expectation()

    # Prep the inputs as tensors
    circuit_tensor = tfq.convert_to_tensor(circuits)
    values_tensor = tf.convert_to_tensor(
        np.random.uniform(0, 2 * np.pi, (n_circuits, 1)).astype(np.float32))

    # Use TensorFlow GradientTape to track gradients.
    with tf.GradientTape() as g:
        g.watch(values_tensor)
        forward = expectation(circuit_tensor,
                              operators=op,
                              symbol_names=[symbol],
                              symbol_values=values_tensor)

    # Return variance of gradients across all circuits.
    grads = g.gradient(forward, values_tensor)
    grad_var = tf.math.reduce_std(grads, axis=0)
    return grad_var.numpy()[0]

3.1 راه اندازی و اجرا کنید

تعداد مدارهای تصادفی را برای تولید به همراه عمق آنها و مقدار کیوبیت هایی که باید روی آنها عمل کنند انتخاب کنید. سپس نتایج را رسم کنید.

n_qubits = [2 * i for i in range(2, 7)
           ]  # Ranges studied in paper are between 2 and 24.
depth = 50  # Ranges studied in paper are between 50 and 500.
n_circuits = 200
theta_var = []

for n in n_qubits:
    # Generate the random circuits and observable for the given n.
    qubits = cirq.GridQubit.rect(1, n)
    symbol = sympy.Symbol('theta')
    circuits = [
        generate_random_qnn(qubits, symbol, depth) for _ in range(n_circuits)
    ]
    op = cirq.Z(qubits[0]) * cirq.Z(qubits[1])
    theta_var.append(process_batch(circuits, symbol, op))

plt.semilogy(n_qubits, theta_var)
plt.title('Gradient Variance in QNNs')
plt.xlabel('n_qubits')
plt.xticks(n_qubits)
plt.ylabel('$\\partial \\theta$ variance')
plt.show()

WARNING:tensorflow:5 out of the last 5 calls to <function Adjoint.differentiate_analytic at 0x7f9e3b5c68c0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for  more details.

png

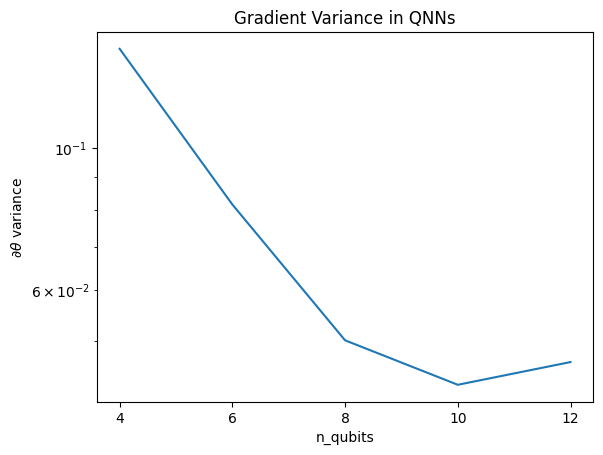
این نمودار نشان می دهد که برای مشکلات یادگیری ماشین کوانتومی، نمی توان به سادگی یک QNN ansatz تصادفی را حدس زد و به بهترین ها امیدوار بود. برخی ساختارها باید در مدار مدل وجود داشته باشد تا گرادیان ها تا جایی که یادگیری ممکن است تغییر کند.

4. اکتشافی

یک اکتشافی جالب توسط Grant، 2019 به فرد اجازه می دهد تا خیلی نزدیک به تصادفی شروع کند، اما نه کاملاً. با استفاده از مدارهای مشابه McClean و همکاران، نویسندگان یک تکنیک اولیه متفاوت را برای پارامترهای کنترل کلاسیک پیشنهاد می‌کنند تا از فلات بی‌ثمر جلوگیری شود. تکنیک مقداردهی اولیه، برخی از لایه‌ها را با پارامترهای کنترلی کاملاً تصادفی شروع می‌کند - اما در لایه‌های بلافاصله بعد، پارامترهایی را انتخاب کنید که تبدیل اولیه ایجاد شده توسط چند لایه اول لغو شود. نویسندگان این را بلوک هویت می نامند.

مزیت این اکتشافی این است که با تغییر تنها یک پارامتر، تمام بلوک های دیگر خارج از بلوک فعلی به عنوان هویت باقی می مانند - و سیگنال گرادیان بسیار قوی تر از قبل می آید. این به کاربر اجازه می دهد تا متغیرها و بلوک ها را برای دریافت سیگنال گرادیان قوی تغییر دهد و انتخاب کند. این اکتشافی مانع از افتادن کاربر به یک فلات بی‌حاصل در مرحله آموزش نمی‌شود (و به‌روزرسانی کاملاً همزمان را محدود می‌کند)، فقط تضمین می‌کند که می‌توانید خارج از فلات شروع کنید.

4.1 ساخت QNN جدید

اکنون یک تابع برای تولید QNNهای بلوک هویت بسازید. این پیاده سازی کمی متفاوت از اجرای مقاله است. در حال حاضر، به رفتار گرادیان یک پارامتر نگاه کنید تا با McClean و همکارانش مطابقت داشته باشد، بنابراین می توان برخی از ساده سازی ها را انجام داد.

برای تولید بلوک هویت و آموزش مدل، معمولاً به \(U1(\theta_{1a}) U1(\theta_{1b})^{\dagger}\) نیاز دارید و نه \(U1(\theta_1) U1(\theta_1)^{\dagger}\). در ابتدا \(\theta_{1a}\) و \(\theta_{1b}\) زوایای یکسانی هستند اما به طور مستقل یاد می گیرند. در غیر این صورت، شما همیشه هویت را حتی پس از آموزش به دست خواهید آورد. انتخاب تعداد بلوک های هویت تجربی است. هر چه بلوک عمیق تر باشد، واریانس در وسط بلوک کمتر است. اما در ابتدا و انتهای بلوک، واریانس گرادیان پارامترها باید زیاد باشد.

def generate_identity_qnn(qubits, symbol, block_depth, total_depth):
    """Generate random QNN's with the same structure from Grant et al."""
    circuit = cirq.Circuit()

    # Generate initial block with symbol.
    prep_and_U = generate_random_qnn(qubits, symbol, block_depth)
    circuit += prep_and_U

    # Generate dagger of initial block without symbol.
    U_dagger = (prep_and_U[1:])**-1
    circuit += cirq.resolve_parameters(
        U_dagger, param_resolver={symbol: np.random.uniform() * 2 * np.pi})

    for d in range(total_depth - 1):
        # Get a random QNN.
        prep_and_U_circuit = generate_random_qnn(
            qubits,
            np.random.uniform() * 2 * np.pi, block_depth)

        # Remove the state-prep component
        U_circuit = prep_and_U_circuit[1:]

        # Add U
        circuit += U_circuit

        # Add U^dagger
        circuit += U_circuit**-1

    return circuit


generate_identity_qnn(cirq.GridQubit.rect(1, 3), sympy.Symbol('theta'), 2, 2)

4.2 مقایسه

در اینجا می توانید ببینید که اکتشافی به جلوگیری از ناپدید شدن واریانس گرادیان به سرعت کمک می کند:

block_depth = 10
total_depth = 5

heuristic_theta_var = []

for n in n_qubits:
    # Generate the identity block circuits and observable for the given n.
    qubits = cirq.GridQubit.rect(1, n)
    symbol = sympy.Symbol('theta')
    circuits = [
        generate_identity_qnn(qubits, symbol, block_depth, total_depth)
        for _ in range(n_circuits)
    ]
    op = cirq.Z(qubits[0]) * cirq.Z(qubits[1])
    heuristic_theta_var.append(process_batch(circuits, symbol, op))

plt.semilogy(n_qubits, theta_var)
plt.semilogy(n_qubits, heuristic_theta_var)
plt.title('Heuristic vs. Random')
plt.xlabel('n_qubits')
plt.xticks(n_qubits)
plt.ylabel('$\\partial \\theta$ variance')
plt.show()

WARNING:tensorflow:6 out of the last 6 calls to <function Adjoint.differentiate_analytic at 0x7f9e3b5c68c0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for  more details.

png

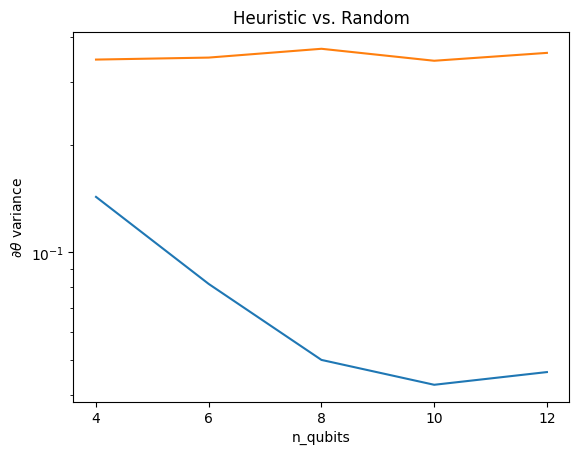
این یک پیشرفت عالی در دریافت سیگنال‌های گرادیان قوی‌تر از QNN‌های تصادفی (تقریباً) است.