 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar libreta Descargar libreta |
En este ejemplo, explorará el resultado de McClean, 2019 que dice que no cualquier estructura de red neuronal cuántica funcionará bien en lo que respecta al aprendizaje. En particular, verá que cierta gran familia de circuitos cuánticos aleatorios no sirven como buenas redes neuronales cuánticas, porque tienen gradientes que desaparecen en casi todas partes. En este ejemplo, no entrenará ningún modelo para un problema de aprendizaje específico, sino que se centrará en el problema más simple de comprender los comportamientos de los gradientes.
Configuración
pip install tensorflow==2.7.0
Instale TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Ahora importa TensorFlow y las dependencias del módulo:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
np.random.seed(1234)
2022-02-04 12:15:43.355568: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Resumen
Circuitos cuánticos aleatorios con muchos bloques que se ven así (\(R_{P}(\theta)\) es una rotación aleatoria de Pauli):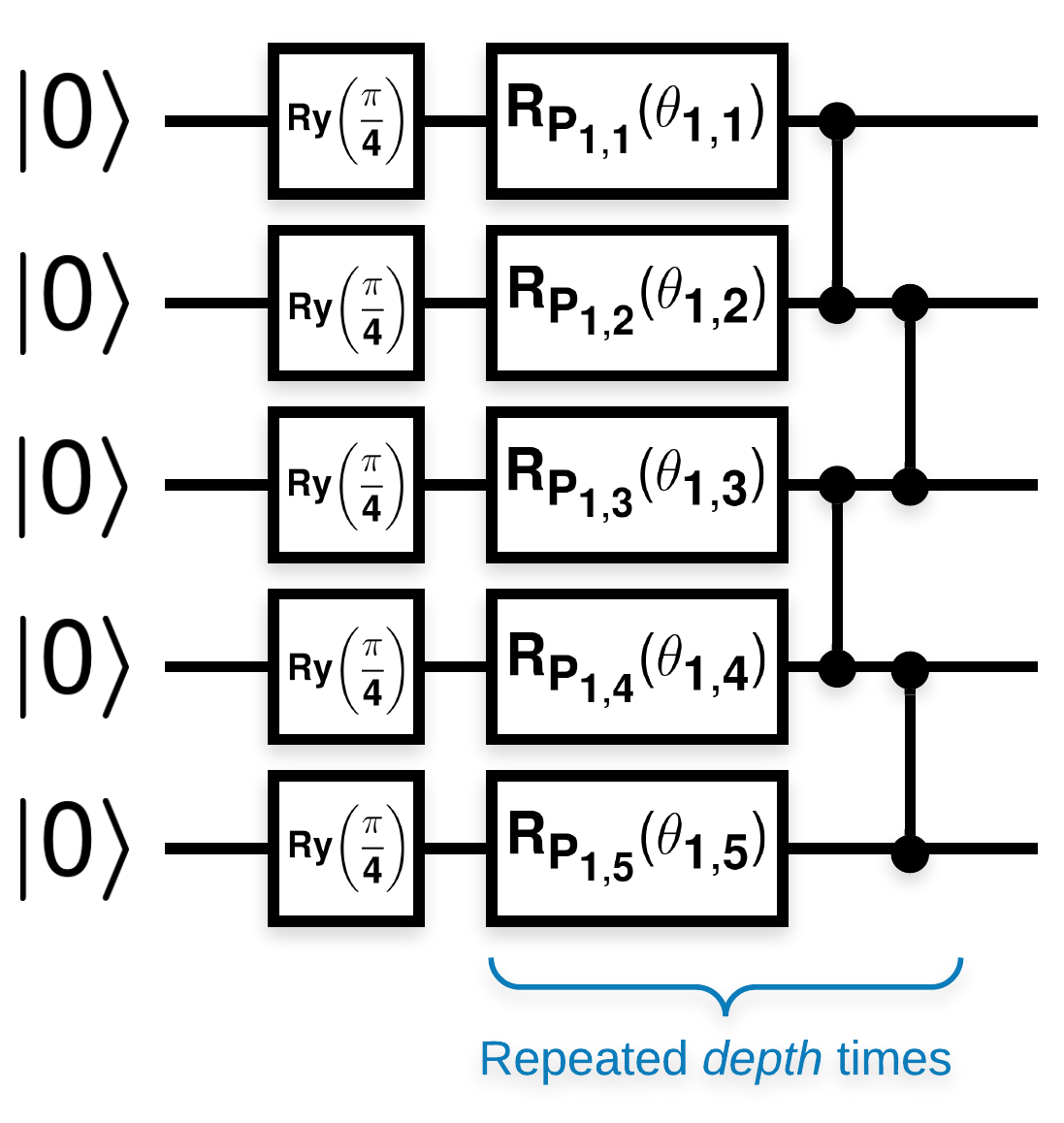
Donde si \(f(x)\) se define como el valor esperado wrt \(Z_{a}Z_{b}\) para cualquier qubits \(a\) y \(b\), entonces existe el problema de que \(f'(x)\) tiene una media muy cercana a 0 y no varía mucho. Verás esto a continuación:
2. Generación de circuitos aleatorios
La construcción del documento es fácil de seguir. Lo siguiente implementa una función simple que genera un circuito cuántico aleatorio, a veces denominado red neuronal cuántica (QNN), con la profundidad dada en un conjunto de qubits:
def generate_random_qnn(qubits, symbol, depth):
"""Generate random QNN's with the same structure from McClean et al."""
circuit = cirq.Circuit()
for qubit in qubits:
circuit += cirq.ry(np.pi / 4.0)(qubit)
for d in range(depth):
# Add a series of single qubit rotations.
for i, qubit in enumerate(qubits):
random_n = np.random.uniform()
random_rot = np.random.uniform(
) * 2.0 * np.pi if i != 0 or d != 0 else symbol
if random_n > 2. / 3.:
# Add a Z.
circuit += cirq.rz(random_rot)(qubit)
elif random_n > 1. / 3.:
# Add a Y.
circuit += cirq.ry(random_rot)(qubit)
else:
# Add a X.
circuit += cirq.rx(random_rot)(qubit)
# Add CZ ladder.
for src, dest in zip(qubits, qubits[1:]):
circuit += cirq.CZ(src, dest)
return circuit
generate_random_qnn(cirq.GridQubit.rect(1, 3), sympy.Symbol('theta'), 2)
Los autores investigan el gradiente de un solo parámetro \(\theta_{1,1}\). Sigamos colocando un sympy.Symbol en el circuito donde estaría \(\theta_{1,1}\) . Dado que los autores no analizan las estadísticas de ningún otro símbolo en el circuito, reemplácelos con valores aleatorios ahora en lugar de más adelante.
3. Hacer funcionar los circuitos
Genere algunos de estos circuitos junto con un observable para probar la afirmación de que los gradientes no varían mucho. Primero, genere un lote de circuitos aleatorios. Elija un observable ZZ aleatorio y calcule por lotes los gradientes y la varianza con TensorFlow Quantum.
3.1 Cálculo de la varianza del lote
Escribamos una función auxiliar que calcule la varianza del gradiente de un observable dado sobre un lote de circuitos:
def process_batch(circuits, symbol, op):
"""Compute the variance of a batch of expectations w.r.t. op on each circuit that
contains `symbol`. Note that this method sets up a new compute graph every time it is
called so it isn't as performant as possible."""
# Setup a simple layer to batch compute the expectation gradients.
expectation = tfq.layers.Expectation()
# Prep the inputs as tensors
circuit_tensor = tfq.convert_to_tensor(circuits)
values_tensor = tf.convert_to_tensor(
np.random.uniform(0, 2 * np.pi, (n_circuits, 1)).astype(np.float32))
# Use TensorFlow GradientTape to track gradients.
with tf.GradientTape() as g:
g.watch(values_tensor)
forward = expectation(circuit_tensor,
operators=op,
symbol_names=[symbol],
symbol_values=values_tensor)
# Return variance of gradients across all circuits.
grads = g.gradient(forward, values_tensor)
grad_var = tf.math.reduce_std(grads, axis=0)
return grad_var.numpy()[0]
3.1 Configurar y ejecutar
Elija la cantidad de circuitos aleatorios para generar junto con su profundidad y la cantidad de qubits sobre los que deben actuar. Luego grafica los resultados.
n_qubits = [2 * i for i in range(2, 7)
] # Ranges studied in paper are between 2 and 24.
depth = 50 # Ranges studied in paper are between 50 and 500.
n_circuits = 200
theta_var = []
for n in n_qubits:
# Generate the random circuits and observable for the given n.
qubits = cirq.GridQubit.rect(1, n)
symbol = sympy.Symbol('theta')
circuits = [
generate_random_qnn(qubits, symbol, depth) for _ in range(n_circuits)
]
op = cirq.Z(qubits[0]) * cirq.Z(qubits[1])
theta_var.append(process_batch(circuits, symbol, op))
plt.semilogy(n_qubits, theta_var)
plt.title('Gradient Variance in QNNs')
plt.xlabel('n_qubits')
plt.xticks(n_qubits)
plt.ylabel('$\\partial \\theta$ variance')
plt.show()
WARNING:tensorflow:5 out of the last 5 calls to <function Adjoint.differentiate_analytic at 0x7f9e3b5c68c0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details.
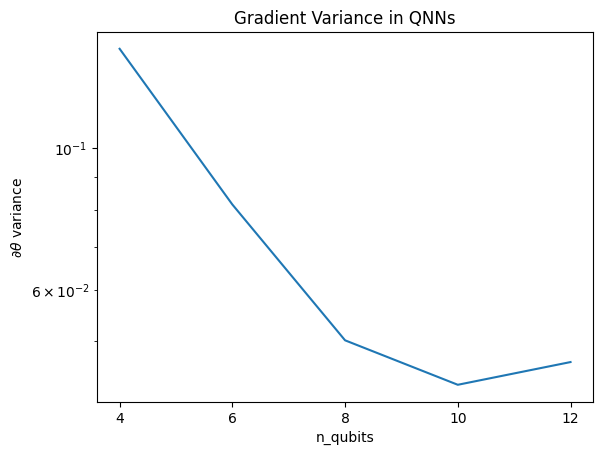
Esta gráfica muestra que para los problemas de aprendizaje automático cuántico, no puede simplemente adivinar un QNN ansatz aleatorio y esperar lo mejor. Debe haber alguna estructura presente en el circuito modelo para que los gradientes varíen hasta el punto en que pueda ocurrir el aprendizaje.
4. Heurística
Una heurística interesante de Grant, 2019 permite comenzar muy cerca del azar, pero no del todo. Usando los mismos circuitos que McClean et al., los autores proponen una técnica de inicialización diferente para los parámetros de control clásicos para evitar mesetas estériles. La técnica de inicialización inicia algunas capas con parámetros de control totalmente aleatorios, pero, en las capas inmediatamente siguientes, elige parámetros de modo que se deshaga la transformación inicial realizada por las primeras capas. Los autores llaman a esto un bloqueo de identidad .
La ventaja de esta heurística es que, al cambiar un solo parámetro, todos los demás bloques fuera del bloque actual seguirán siendo la identidad, y la señal de gradiente llega mucho más fuerte que antes. Esto le permite al usuario elegir qué variables y bloques modificar para obtener una señal de gradiente fuerte. Esta heurística no evita que el usuario caiga en una meseta estéril durante la fase de entrenamiento (y restringe una actualización totalmente simultánea), solo garantiza que puede comenzar fuera de una meseta.
4.1 Nueva construcción de QNN
Ahora construya una función para generar QNN de bloque de identidad. Esta implementación es ligeramente diferente a la del papel. Por ahora, mire el comportamiento del gradiente de un solo parámetro para que sea consistente con McClean et al, por lo que se pueden hacer algunas simplificaciones.
Para generar un bloque de identidad y entrenar el modelo, generalmente necesita \(U1(\theta_{1a}) U1(\theta_{1b})^{\dagger}\) y no \(U1(\theta_1) U1(\theta_1)^{\dagger}\). Inicialmente \(\theta_{1a}\) y \(\theta_{1b}\) son los mismos ángulos, pero se aprenden de forma independiente. De lo contrario, siempre obtendrá la identidad incluso después del entrenamiento. La elección del número de bloques de identidad es empírica. Cuanto más profundo es el bloque, menor es la variación en el medio del bloque. Pero al principio y al final del bloque, la varianza de los gradientes de los parámetros debe ser grande.
def generate_identity_qnn(qubits, symbol, block_depth, total_depth):
"""Generate random QNN's with the same structure from Grant et al."""
circuit = cirq.Circuit()
# Generate initial block with symbol.
prep_and_U = generate_random_qnn(qubits, symbol, block_depth)
circuit += prep_and_U
# Generate dagger of initial block without symbol.
U_dagger = (prep_and_U[1:])**-1
circuit += cirq.resolve_parameters(
U_dagger, param_resolver={symbol: np.random.uniform() * 2 * np.pi})
for d in range(total_depth - 1):
# Get a random QNN.
prep_and_U_circuit = generate_random_qnn(
qubits,
np.random.uniform() * 2 * np.pi, block_depth)
# Remove the state-prep component
U_circuit = prep_and_U_circuit[1:]
# Add U
circuit += U_circuit
# Add U^dagger
circuit += U_circuit**-1
return circuit
generate_identity_qnn(cirq.GridQubit.rect(1, 3), sympy.Symbol('theta'), 2, 2)
4.2 Comparación
Aquí puede ver que la heurística ayuda a evitar que la varianza del gradiente desaparezca tan rápidamente:
block_depth = 10
total_depth = 5
heuristic_theta_var = []
for n in n_qubits:
# Generate the identity block circuits and observable for the given n.
qubits = cirq.GridQubit.rect(1, n)
symbol = sympy.Symbol('theta')
circuits = [
generate_identity_qnn(qubits, symbol, block_depth, total_depth)
for _ in range(n_circuits)
]
op = cirq.Z(qubits[0]) * cirq.Z(qubits[1])
heuristic_theta_var.append(process_batch(circuits, symbol, op))
plt.semilogy(n_qubits, theta_var)
plt.semilogy(n_qubits, heuristic_theta_var)
plt.title('Heuristic vs. Random')
plt.xlabel('n_qubits')
plt.xticks(n_qubits)
plt.ylabel('$\\partial \\theta$ variance')
plt.show()
WARNING:tensorflow:6 out of the last 6 calls to <function Adjoint.differentiate_analytic at 0x7f9e3b5c68c0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details.
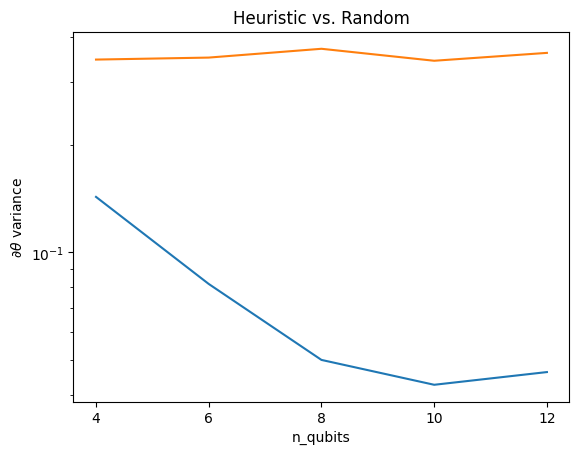
Esta es una gran mejora para obtener señales de gradiente más fuertes de QNN (casi) aleatorios.
