 TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
pip install -q -U jax jaxlibpip install -q -Uq oryx -Ipip install -q tfp-nightly --upgrade
from functools import partial
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')
import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
import oryx
Olasılıksal programlama, bir programlama dilindeki özellikleri kullanarak olasılıklı modelleri ifade edebileceğimiz fikridir. Bayes çıkarımı veya marjinalleştirme gibi görevler daha sonra dil özellikleri olarak sağlanır ve potansiyel olarak otomatikleştirilebilir.
Oryx, olasılık programlarının sadece Python fonksiyonları olarak ifade edildiği olasılıksal bir programlama sistemi sağlar; bu programlar daha sonra JAX'takiler gibi birleştirilebilir işlev dönüşümleriyle dönüştürülür! Buradaki fikir, basit programlarla (rastgele bir normalden örnekleme gibi) başlamak ve bunları bir araya getirerek modeller oluşturmaktır (Bayesian sinir ağı gibi). Oryx en PPL tasarımının önemli bir nokta JAX 'Zaten yazacağımı işlevleri ve kullanım gibi görünmek programları sağlamaktır, ancak bunların dönüşümleri haberdar etmek açıklamalı.
Önce Oryx'in temel PPL işlevselliğini içe aktaralım.
from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest
Oryx'te olasılık programları nelerdir?
Oryx'te olasılık programları, JAX değerleri ve sözde rasgele anahtarlar üzerinde çalışan ve rastgele bir örnek döndüren saf Python işlevleridir. Tasarım gereği, onlar gibi dönüşümler ile uyumlu jit ve vmap . Ancak, Oryx olasılık programlama sistemi faydalı şekillerde açıklama işlevleri sağlayacak araçlar sunar.
Saf fonksiyonların JAX felsefesi takiben, Oryx olasılık programı JAX alır Python fonksiyonudur PRNGKey ilk argüman ve daha sonra klima bağımsız değişkenler herhangi bir sayı olarak. Fonksiyonunun çıktısı, bir "örnek" ve için geçerli olan aynı kısıtlamalar denir jit -ed ve vmap -ed fonksiyonlar olasılık programların (örneğin hiçbir veri bağımlı kontrol akışı, hiçbir yan etkisi, vs.) için de geçerlidir. Bu, programın yürütülmesine dahil olan değerler de dahil olmak üzere tüm yürütme izinin bir 'örnek' olduğu birçok zorunlu olasılıklı programlama sisteminden farklıdır. Biz Oryx kullanarak dahili değerleri nasıl erişebileceğini sonra göreceğiz joint_sample aşağıda ele.
Program :: PRNGKey -> ... -> Sample
İşte "merhaba dünya" programı olduğuna dair gelen numuneler log-normal dağılım .
def log_normal(key):
return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.) 0.8139614 /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
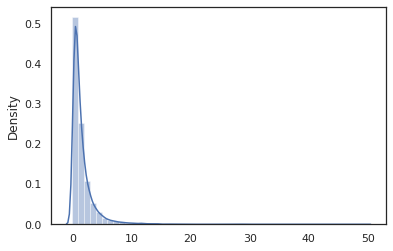
log_normal işlevi etrafında ince bir sarıcı Tensorflow Olasılık (TFP) yerine çağrı, dağıtım tfd.Normal(0., 1.).sample , kullandığımız random_variable yerine. Daha sonra göreceğimiz gibi, random_variable diğer yararlı işlevselliği ile birlikte olasılık programlarına nesneleri dönüştürmek için bize sağlar.
Biz dönüştürebilirsiniz log_normal kullanarak bir günlük yoğunluklu fonksiyonu içine log_prob dönüşümü:
print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()
-0.9189385
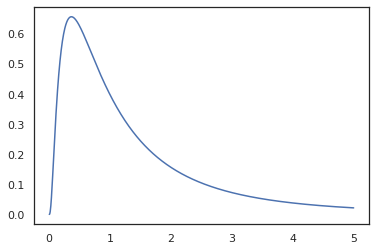
Birlikte işlevini açıklamalı ettik Çünkü random_variable , log_prob bir çağrı olduğunu bilmektedir tfd.Normal(0., 1.).sample ve kullanır tfd.Normal(0., 1.).log_prob baz dağılımını hesaplamak için günlük prob. İşlemek için jnp.exp , ppl.log_prob otomatik değişim-of-değişken hesaplamasında hacim değişiklikleri izleme, bijective fonksiyonlar yoluyla yoğunluğunu hesaplar.
Oryx'nin, biz programları alabilir ve işlev dönüşümleri kullanarak bunları dönüştürmek - örneğin, için jax.jit veya log_prob . Ancak Oryx bunu herhangi bir programla yapamaz; günlük yoğunluk işlevlerini Oryx ile kaydettirmiş örnekleme işlevleri gerektirir. Neyse ki, Oryx otomatik kaydeder TensorFlow Olasılık kendi sisteminde (TFP) dağılımları.
Oryx'in olasılıksal programlama araçları
Oryx, olasılıksal programlamaya yönelik çeşitli fonksiyon dönüşümlerine sahiptir. Çoğunu gözden geçireceğiz ve bazı örnekler vereceğiz. Sonunda, hepsini bir MCMC vaka incelemesinde bir araya getireceğiz. Ayrıca belgelerine başvurabilirsiniz core.ppl.transformations Daha fazla ayrıntı için.
random_variable
random_variable işlevsellik iki ana parçalar vardır, her iki dönüşümler kullanılabilecek bilgilerle Python fonksiyonları annotating üzerinde duruldu.
random_variable'varsayılan kimlik işlevi olarak çalışır, ancak olasılık programs.` içine dönüştürme nesnelere türe özel kayıtlarını kullanabilirsinizÇağrılabilir türleri (Python fonksiyonları, lambdas için
functools.partials, vb) ve keyfiobjects (JAX gibiDeviceArrayler) sadece kendi girişi dönecektir.random_variable(x: object) == x random_variable(f: Callable[...]) == fOryx otomatik kaydeder TensorFlow Olasılık (TFP) dağılımınızın diyoruz olasılık programlarına dönüştürülür dağılımları,
sampleyöntemi.random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235Oryx ayrıca, günlük yoğunluklarının otomatik olarak hesaplanmasını sağlayan JAX izlerine TFP dağıtımı hakkındaki bilgileri gömer.
random_variableisimlerle kutu etiket değerleri, isteğe bağlı sağlayarak, mansap dönüşümler için faydalı halenameanahtar kelime argümanırandom_variable. İçine bir dizi geçiş zamanrandom_variablebir birliktename(örneğinrandom_variable(x, name='x')), sadece değeri ve döner bu etiketler. Biz çağrılabilir veya TFP dağılımı, içinde geçersenizrandom_variabledöner bir programla etiketler çıkış örneği olduğununame.
Çalıştırıldığında Bu ek açıklamalar programın semantiğini değişmez, ancak dönüştürülmüş sadece (yani programı ile veya kullanılmadan aynı değeri döndürecektir random_variable ).
Her iki işlevsellik parçasını birlikte kullandığımız bir örnek üzerinden gidelim.
def latent_normal(key):
z_key, x_key = random.split(key)
z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)
Bu programda biz ara etiketlediniz z ve x dönüşümleri yapar, joint_sample , intervene , conditional ve graph_replace adları farkında 'z' ve 'x' . Daha sonra her dönüşümün adları nasıl kullandığını tam olarak ele alacağız.
log_prob
log_prob fonksiyonu dönüşümü, log yoğunluk fonksiyonu içine Oryx olasılıksal programı dönüştürür. Bu günlük yoğunluğu işlevi, programdan potansiyel bir örneği girdi olarak alır ve temel alınan örnekleme dağılımı altında günlük yoğunluğunu döndürür.
log_prob :: Program -> (Sample -> LogDensity)
Gibi random_variable , o kadar, TFP dağılımları kaydı otomatik olarak yapılır türlerinin bir kayıt defteri aracılığıyla çalışır log_prob(tfd.Normal(0., 1.)) çağıran tfd.Normal(0., 1.).log_prob . Python fonksiyonları için ise, log_prob ifadeleri örnekleme için JAX ve görünüm kullanarak programı izler. log_prob dönüşüm rasgele değişkenleri dönmek çoğu programlarda, doğrudan veya ters çevrilebilir dönüşümler yoluyla değil programlarına örnek değerler içten döndürülmemesi bu konuda çalışıyor. Programdaki gerekli işlemleri ters yapamıyorsanız, log_prob bir hata atar.
İşte bazı örnekler log_prob çeşitli programlar uygulanmaktadır.
-
log_probdoğrudan TFP dağılımları (ya da diğer kayıtlı türlerinden) örnek ve değerlerini iade programları çalışır.
def normal(key):
return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))
-0.9189385
-
log_prob(örneğin örten fonksiyonları kullanarak rasgele değişebilirlerin dönüşümü programlardan örnekleri log-yoğunlukları hesaplamak mümkünjnp.exp,jnp.tanh,jnp.split).
def log_normal(key):
return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))
-1.159165
Bir örnek hesaplamak için log_normal s' log-yoğunluk, biz ters çevirmek için ilk ihtiyaç exp alarak log Ters log-det jakobiyen kullanarak bir hacim değişikliği düzeltme ekleme sonra numunenin ve exp (bkz değişikliği değişkeni Wikipedia formül).
-
log_probprogramları ile çalışır numunelerin çıkış yapıları, Python sözlükleri veya dizilerini hoşlandığımı.
def normal_2d(key):
x = random_variable(
tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
x1, x2 = jnp.split(x, 2, 0)
return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))
{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546
-
log_probhem ileri hem de ters değerlerinin hesaplanması, fonksiyon takip hesaplama grafiğini yürür (ve log-det Jakobiyen) gerektiğinde değişkenlerin iyi tanımlanmış bir değişikliği ile baz örnek değerleri ile verilen değerler bağlamak için bir girişim. Aşağıdaki örnek programı alın:
def complex_program(key):
k1, k2 = random.split(key)
z = random_variable(tfd.Normal(0., 1.))(k1)
x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))
(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32)) -1.0967848
Bu programda, örnek x şartlı ilgili z biz, yani değerini mi z biz log-yoğunluk hesaplamak için önce x . Bununla birlikte, işlem için z , öncelikle çevirmek zorunda jnp.exp tatbik z . Bu nedenle, log-yoğunlukları hesaplamak için x ve z , log_prob birinci çıkışına ters birinci ihtiyaçlarına ve sonra ileri doğru geçmesi jax.nn.relu ortalama hesaplamak için p(x | z) .
Hakkında daha fazla bilgi için log_prob , sen başvurabilirsiniz core.interpreters.log_prob . Uygulamada, log_prob yakından kapalı dayanır inverse JAX dönüşümü; hakkında daha fazla bilgi edinmek için inverse bkz core.interpreters.inverse .
joint_sample
Daha karmaşık ve ilginç programlar tanımlamak için bazı gizli rastgele değişkenler, yani gözlemlenmemiş değerlere sahip rastgele değişkenler kullanacağız. En bakınız olsun latent_normal programı bu numuneler, bir rasgele değer z başka bir rasgele değer ortalama olarak kullanılır x .
def latent_normal(key):
z_key, x_key = random.split(key)
z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)
Bu programda, z sadece aramaya olsaydı gizli böyledir latent_normal(random.PRNGKey(0)) biz gerçek değerini bilemeyiz z oluşturmaktan sorumludur x .
joint_sample bir dönüşüm olduğunu başka bir programa dönüşümler bir program onların değerlerine döner bir sözlük haritalama dize adları (etiketleri). Çalışmak için, dönüştürülmüş fonksiyonun çıktısında görünmelerini sağlamak için gizli değişkenleri etiketlediğimizden emin olmamız gerekir.
joint_sample(latent_normal)(random.PRNGKey(0))
{'x': DeviceArray(0.01873656, dtype=float32),
'z': DeviceArray(0.14389044, dtype=float32)}
O Not joint_sample dönüşümler başka bir programa bir program örnekleri onun gizli değerler üzerinde ortak dağıtım, bu yüzden daha da taşıyabileceğini düşünür. MCMC ve VI gibi algoritmalar için, çıkarım prosedürünün bir parçası olarak ortak dağılımın log olasılığını hesaplamak yaygındır. log_prob(latent_normal) dışarı marjinalleştirmekten gerektirdiği için iş yapmaz z , ama biz kullanabilirsiniz log_prob(joint_sample(latent_normal)) .
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))
-50.03529 -5049.535
Bu tür bir ortak model olduğu için Oryx da vardır joint_log_prob sadece bileşimdir dönüşümü log_prob ve joint_sample .
print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))
-50.03529 -5049.535
block
block dönüşümü bir program ve adları sırayla alır ve aynı alt dönüşümleri (gibi olması hariç davranır bir programı döner joint_sample ), Resim isimleri göz ardı edilir. Burada bir örnek block kullanışlı olasılıkla örneklenen "bloke edici" değerleri ile gizli değişkenleri üzerinde daha önceden bir ortak dağıtım dönüştürmektedir. Örneğin, almak latent_normal önce çizer, z ~ N(0, 1) daha sonra, bir x | z ~ N(z, 1e-1) . block(latent_normal, names=['x']) deri bir programdır x adı yaptığımız Öyleyse joint_sample(block(latent_normal, names=['x'])) , sadece bir sözlük elde z içinde .
blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))
{'z': DeviceArray(0.14389044, dtype=float32)}
intervene
intervene dışarıdan değerleriyle bir olasılık programında dönüşüm clobbers örnekleri. Bizim için geri gidiş latent_normal programı, en biz aynı programı çalıştıran ilgilenen ama istiyorum diyelim z yeni bir program yazmaktan daha 4. Rather'ın sabitlenmiş olması, kullanabileceğimiz intervene değerini geçersiz kılmak için z .
intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
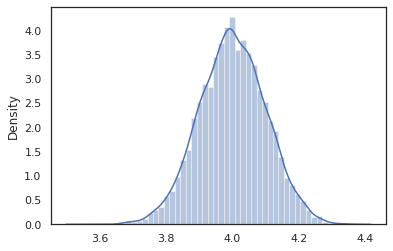
intervened ile ilgili fonksiyon örnekleri p(x | do(z = 4)) biz zaman sadece standart bir normal dağılım 4 ° C'de merkezli olan intervene belirli bir değeri, bu değer, artık rastgele değişken olarak kabul edilir. A Bu aracı z değeri ise etiketlenmeyeceksiniz olarak çalıştırma intervened .
conditional
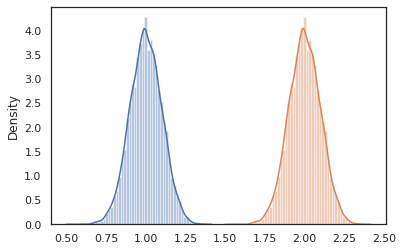
conditional dönüşümler örnekleri içine değerleri latent bir programın o gizli değerlere koşulları. Bizim dönersek latent_normal programı, numuneler p(x) bir latent ile z , bir koşullu programı haline dönüştürebilir p(x | z) .
cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()
99.87485 49.874847 /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning) /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
nest
Daha karmaşık programlar oluşturmak için olasılık programları oluşturmaya başladığımızda, bazı önemli mantığı olan işlevleri yeniden kullanmak yaygındır. Biz Bayes nöral ağ kurmak istiyorsanız Örneğin, önemli bir olabileceğini dense program örnekleri ağırlıklar ve yürütür öne geçip söyledi.
Biz fonksiyonlarını yeniden Ancak, biz gibi dönüşümler tarafından izin verilmeyen son programda, yinelenen Etiketlenmiş değerlerle sonunda olabilir joint_sample . Biz kullanabilirsiniz nest etiketi oluşturmak için adlandırılmış kapsam içine herhangi bir örnek iç içe bir sözlüğe eklenecektir burada "kapsamları".
def f(key):
return random_variable(tfd.Normal(0., 1.), name='x')(key)
def g(key):
k1, k2 = random.split(key)
return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))
{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }
Örnek olay: Bayes sinir ağı
Let klasik sınıflandırmak için bir Bayes sinir ağı eğitim bizim el denemek Fisher İris veri kümesi. Nispeten küçük ve düşük boyutludur, bu nedenle MCMC ile posteriordan doğrudan örneklemeyi deneyebiliriz.
İlk olarak, veri kümesini ve bazı ek yardımcı programları Oryx'ten içe aktaralım.
from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
from oryx.experimental import mcmc
from oryx.util import summary, get_summaries
Ağırlıklar ve önyargı üzerinde normal önceliğe sahip olacak yoğun bir katman uygulayarak başlıyoruz. Bunu yapmak için, ilk olarak bir tanımlar dense istenen çıkış boyutu ve aktivasyon fonksiyonuna alır yüksek sıra işlevini. dense işlevi koşullu dağılım gösteren bir olasılık programı döner p(h | x) h yoğun bir tabaka çıkışı olan ve x de girilir. Daha sonra ilk örnekleri ağırlık ve yanlılık ve uygular x .
def dense(dim_out, activation=jax.nn.relu):
def forward(key, x):
dim_in = x.shape[-1]
w_key, b_key = random.split(key)
w = random_variable(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
name='w')(w_key)
b = random_variable(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
name='b')(b_key)
return activation(jnp.dot(w, x) + b)
return forward
Birkaç oluşturmak için dense katmanları bir araya, biz uygulayacak mlp gizli boyutlarının listesi ve sınıfların bir dizi alır (katmanlı algılayıcı) yüksek mertebeden fonksiyonu. Bu defalarca çağırdığı bir program döndürür dense uygun kullanarak hidden_size ve son olarak nihai katmanda her sınıf için logits döndürür. Kullanımına dikkat nest her katman için isim kapsamları oluşturur.
def mlp(hidden_sizes, num_classes):
num_hidden = len(hidden_sizes)
def forward(key, x):
keys = random.split(key, num_hidden + 1)
for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
logits = nest(dense(num_classes, activation=lambda x: x),
scope=f'layer_{num_hidden + 1}')(keys[-1], x)
return logits
return forward
Tam modeli uygulamak için etiketleri kategorik rastgele değişkenler olarak modellememiz gerekecek. Biz tanımlayacağız predict bir veri kümesi alır işlevi xs sonra içine geçirilir (özellikler) mlp kullanılarak vmap . Kullandığımız zaman vmap(partial(mlp, mlp_key)) , ağırlıklarla tek bir dizi örnek, ancak girdi her ileri doğru geçiş harita xs . Bu bir dizi üretir logits bağımsız kategorik dağılımları parameterizes.
def predict(mlp):
def forward(key, xs):
mlp_key, label_key = random.split(key)
logits = vmap(partial(mlp, mlp_key))(xs)
return random_variable(
tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
return forward
Tam model bu! Verileri verilen BNN ağırlıklarının arkasını örneklemek için MCMC'yi kullanalım; İlk kullandığımız bir BNN "şablon" inşa mlp .
bnn = mlp([200, 200], num_classes)
Bizim Markov zinciri için bir başlangıç noktası oluşturmak için, kullanabilir joint_sample bir kukla girişli.
weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())
dict_keys(['layer_1', 'layer_2', 'layer_3'])
Ortak dağılım log olasılığının hesaplanması birçok çıkarım algoritması için yeterlidir. Şimdi biz gözlemlemek diyelim x ve posterior örneklemek istiyoruz p(z | x) . Karmaşık dağılımlar için, biz marginalize mümkün olmayacaktır x (olsa için latent_normal ama biz) biz normalleştirilmemiş günlük yoğunluğu hesaplayabilir log p(z, x) x , belirli bir değere sabitlenir. Posterioru örneklemek için MCMC ile normalleştirilmemiş log olasılığını kullanabiliriz. Bu "sabitlenmiş" log prob fonksiyonunu yazalım.
def target_log_prob(weights):
return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)
Şimdi kullanabilirsiniz tfp.mcmc bizim normalize edilmemiş günlük yoğunluk fonksiyonunu kullanarak posterior örnek. Bizim iç içe ağırlıkları "düzleştirilmiş" sürümünü kullanmak gerekecek Not ile uyumlu olacak şekilde sözlüğe tfp.mcmc biz dümdüz ve unflatten için Jax'in ağaç araçları kullanmak, böylece.
@jit
def run_chain(key, weights):
flat_state, sample_tree = jax.tree_flatten(weights)
def flat_log_prob(*states):
return target_log_prob(jax.tree_unflatten(sample_tree, states))
def trace_fn(_, results):
return results.inner_results.accepted_results.target_log_prob
flat_states, log_probs = tfp.mcmc.sample_chain(
1000,
num_burnin_steps=9000,
kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
9000, target_accept_prob=0.7),
trace_fn=trace_fn,
current_state=flat_state,
seed=key)
samples = jax.tree_unflatten(sample_tree, flat_states)
return samples, log_probs
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)
plt.plot(log_probs)
plt.show()
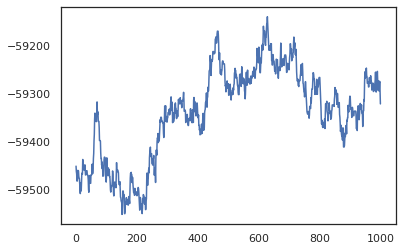
Eğitim doğruluğunun bir Bayes modeli ortalama (BMA) tahminini almak için örneklerimizi kullanabiliriz. Bunu hesaplamak için, kullanabilirsiniz intervene ile bnn anahtarından örneklenir olanların yerine "inject" arka ağırlıklarına. Her arka numune için her bir veri noktası için logits hesaplamak için, iki katına çıkarabilir vmap üzerinde posterior_weights ve features .
output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)
print('Average sample accuracy:', (
output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())
Average sample accuracy: 0.9874067 BMA accuracy: 0.99333334
Çözüm
Oryx'te olasılık programları, girdi olarak (sözde) rastgeleliği alan JAX işlevleridir. Oryx'in JAX'ın fonksiyon dönüştürme sistemiyle sıkı entegrasyonu nedeniyle, JAX kodu yazıyormuş gibi olasılıklı programları yazabilir ve değiştirebiliriz. Bu, karmaşık modeller oluşturmak ve çıkarım yapmak için basit ama esnek bir sistemle sonuçlanır.
