การเขียนโปรแกรมความน่าจะเป็นใน Oryx

ดูบน TensorFlow.org

ทำงานใน Google Colab

ดูแหล่งที่มาบน GitHub

ดาวน์โหลดโน๊ตบุ๊ค

pip install -q -U jax jaxlib
pip install -q -Uq oryx -I
pip install -q tfp-nightly --upgrade

from functools import partial

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')

import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random

from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions

import oryx

การเขียนโปรแกรมความน่าจะเป็นเป็นแนวคิดที่เราสามารถแสดงแบบจำลองความน่าจะเป็นโดยใช้คุณสมบัติจากภาษาการเขียนโปรแกรม งานต่างๆ เช่น การอนุมานแบบเบเซียนหรือการทำให้เป็นชายขอบ จะถูกจัดเตรียมเป็นคุณลักษณะทางภาษา และสามารถดำเนินการอัตโนมัติได้

Oryx จัดเตรียมระบบการเขียนโปรแกรมความน่าจะเป็นซึ่งโปรแกรมความน่าจะเป็นจะแสดงเป็นฟังก์ชัน Python โปรแกรมเหล่านี้จะถูกแปลงผ่านการแปลงฟังก์ชันที่เขียนได้เช่นเดียวกับใน JAX! แนวคิดคือการเริ่มต้นด้วยโปรแกรมง่ายๆ (เช่น การสุ่มตัวอย่างจากค่าปกติแบบสุ่ม) และประกอบเข้าด้วยกันเพื่อสร้างแบบจำลอง (เช่น โครงข่ายประสาทเทียมแบบเบย์) จุดสำคัญของการออกแบบ PPL Oryx คือการเปิดใช้งานโปรแกรมให้มีลักษณะเหมือนฟังก์ชั่นที่คุณต้องการแล้วเขียนและการใช้งานใน JAX แต่ข้อเขียนที่จะทำให้การแปลงรู้ของพวกเขา

อันดับแรก มานำเข้าฟังก์ชัน PPL หลักของ Oryx กันก่อน

from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest

โปรแกรมความน่าจะเป็นใน Oryx คืออะไร?

ใน Oryx โปรแกรมความน่าจะเป็นเป็นเพียงฟังก์ชัน Python แท้ ๆ ที่ทำงานบนค่า JAX และคีย์สุ่มเทียมและส่งคืนตัวอย่างแบบสุ่ม โดยการออกแบบที่พวกเขาจะเข้ากันได้กับการเปลี่ยนแปลงเช่น jit และ vmap อย่างไรก็ตามระบบการเขียนโปรแกรม Oryx น่าจะมีเครื่องมือที่ช่วยให้คุณสามารถใส่คำอธิบายประกอบฟังก์ชั่นของคุณในรูปแบบที่มีประโยชน์

ต่อไปนี้ปรัชญา JAX ของฟังก์ชั่นบริสุทธิ์โปรแกรมน่าจะเป็น Oryx เป็นฟังก์ชั่นหลามที่ใช้ JAX PRNGKey เป็นอาร์กิวเมนต์ครั้งแรกและจำนวนของการขัดแย้งเครื่องใด ๆ ภายหลัง การส่งออกของฟังก์ชั่นที่เรียกว่า "ตัวอย่าง" และข้อ จำกัด เดียวกันกับที่นำไปใช้กับ jit -ed และ vmap ฟังก์ชั่น -ed นำไปใช้กับโปรแกรมที่น่าจะเป็น (เช่นไม่มีการไหลของข้อมูลขึ้นอยู่กับการควบคุมไม่มีผลข้างเคียงอื่น ๆ ) ซึ่งแตกต่างจากระบบการเขียนโปรแกรมความน่าจะเป็นที่จำเป็นหลายอย่าง ซึ่ง 'ตัวอย่าง' คือการติดตามการดำเนินการทั้งหมด รวมถึงค่าภายในของการดำเนินการของโปรแกรม เราจะได้เห็นต่อไปว่า Oryx สามารถเข้าถึงค่าใช้ภายใน joint_sample , กล่าวถึงด้านล่าง

Program :: PRNGKey -> ... -> Sample

นี่คือโปรแกรม "Hello World" ว่ากลุ่มตัวอย่างจาก การกระจายของระบบปกติ

def log_normal(key):
  return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))

print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
0.8139614
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

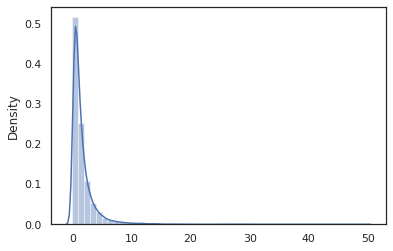
log_normal ฟังก์ชั่นเป็นเสื้อคลุมบาง ๆ รอบ น่าจะเป็น Tensorflow (TFP) กระจาย แต่แทนที่จะเรียก tfd.Normal(0., 1.).sample เราเคยใช้ random_variable แทน ในฐานะที่เราจะเห็นต่อมา random_variable ช่วยให้เราสามารถแปลงวัตถุลงในโปรแกรมน่าจะเป็นพร้อมกับฟังก์ชันการทำงานที่มีประโยชน์อื่น ๆ

เราสามารถแปลง log_normal เป็นฟังก์ชั่นบันทึกความหนาแน่นโดยใช้ log_prob การเปลี่ยนแปลง:

print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()

-0.9189385

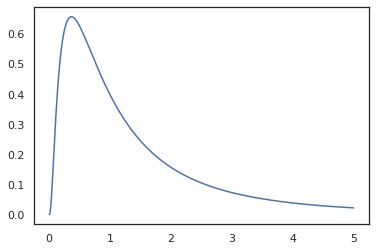
เพราะเราได้ข้อเขียนฟังก์ชั่นที่มี random_variable , log_prob จะทราบว่ามีการโทรไปยัง tfd.Normal(0., 1.).sample และใช้ tfd.Normal(0., 1.).log_prob เพื่อคำนวณการกระจายฐาน บันทึกปัญหา ที่จะจัดการกับ jnp.exp , ppl.log_prob โดยอัตโนมัติคำนวณความหนาแน่นผ่านฟังก์ชั่น bijective การติดตามการเปลี่ยนแปลงปริมาณในการคำนวณการเปลี่ยนแปลงของตัวแปร

ใน Oryx เราสามารถใช้โปรแกรมและเปลี่ยนพวกเขาโดยใช้ฟังก์ชั่นแปลง - ตัวอย่างเช่น jax.jit หรือ log_prob Oryx ไม่สามารถทำได้ด้วยโปรแกรมใดๆ ต้องใช้ฟังก์ชันสุ่มตัวอย่างที่ลงทะเบียนฟังก์ชันความหนาแน่นของบันทึกกับ Oryx โชคดีที่ Oryx โดยอัตโนมัติลงทะเบียน TensorFlow ความน่าจะเป็น (TFP) กระจายในระบบ

เครื่องมือการเขียนโปรแกรมความน่าจะเป็นของ Oryx

Oryx มีการแปลงฟังก์ชันหลายอย่างที่มุ่งสู่การเขียนโปรแกรมความน่าจะเป็น เราจะอธิบายส่วนใหญ่และให้ตัวอย่าง ในตอนท้าย เราจะรวบรวมทั้งหมดไว้ในกรณีศึกษาของ MCMC นอกจากนี้คุณยังสามารถดูเอกสารสำหรับ core.ppl.transformations สำหรับรายละเอียดเพิ่มเติม

random_variable

random_variable มีสองชิ้นหลักของการทำงานทั้งมุ่งเน้นไปที่ฟังก์ชั่น annotating หลามมีข้อมูลที่สามารถใช้ในการแปลง

1. random_variable 'ทำงานเป็นฟังก์ชั่นตัวตนโดยเริ่มต้น แต่สามารถใช้การลงทะเบียนประเภทที่เฉพาะเจาะจงไปยังวัตถุที่แปลงเป็น programs.` ความน่าจะเป็น

   ประเภท callable (ฟังก์ชั่นหลาม lambdas, functools.partial s, ฯลฯ ) และพล object s (เช่น JAX DeviceArray s) มันก็จะกลับมาป้อนข้อมูล

   random_variable(x: object) == x
   random_variable(f: Callable[...]) == f
   

   Oryx โดยอัตโนมัติลงทะเบียน TensorFlow ความน่าจะเป็น (TFP) กระจายซึ่งจะถูกแปลงเป็นโปรแกรมที่น่าจะเป็นที่เรียกร้องการกระจายของ sample วิธีการ

   random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235
   

   Oryx ยังฝังข้อมูลเกี่ยวกับการกระจาย TFP ลงในการติดตาม JAX ซึ่งช่วยให้สามารถคำนวณความหนาแน่นของบันทึกโดยอัตโนมัติ

2. random_variable ค่าแท็กที่สามารถมีชื่อที่ทำให้พวกเขามีประโยชน์สำหรับการแปลงปลายน้ำโดยให้เลือก name โต้แย้งคำหลักเพื่อ random_variable เมื่อเราผ่านอาร์เรย์เข้า random_variable พร้อมกับ name (เช่น random_variable(x, name='x') ) ก็แค่แท็กคุ้มค่าและผลตอบแทนมัน ถ้าเราผ่านในการกระจาย callable หรือ TFP, random_variable ผลตอบแทนโปรแกรมที่แท็กตัวอย่างการส่งออกที่มี name

คำอธิบายประกอบเหล่านี้ไม่ได้เปลี่ยนความหมายของโปรแกรมเมื่อดำเนินการ แต่เมื่อเปลี่ยน (เช่นโปรแกรมจะส่งกลับค่าเดียวกันมีหรือไม่มีการใช้งานของ random_variable )

มาดูตัวอย่างการใช้งานทั้งสองส่วนร่วมกัน

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

ในโปรแกรมนี้เราได้ติดแท็กตัวกลาง z และ x ซึ่งจะทำให้การแปลง joint_sample , intervene , conditional และ graph_replace ตระหนักถึงชื่อ 'z' และ 'x' เราจะมาดูกันว่าการเปลี่ยนแปลงแต่ละครั้งใช้ชื่ออย่างไรในภายหลัง

log_prob

log_prob เปลี่ยนแปลงฟังก์ชันแปลงโปรแกรมน่าจะเป็น Oryx ในการทำงานเข้าสู่ระบบที่มีความหนาแน่นของมัน ฟังก์ชันความหนาแน่นของบันทึกนี้ใช้ตัวอย่างที่เป็นไปได้จากโปรแกรมเป็นอินพุตและส่งคืนความหนาแน่นของบันทึกภายใต้การกระจายตัวอย่างพื้นฐาน

log_prob :: Program -> (Sample -> LogDensity)

เช่นเดียวกับ random_variable ก็ทำงานผ่านรีจิสทรีประเภทที่กระจาย TFP มีการลงทะเบียนโดยอัตโนมัติดังนั้น log_prob(tfd.Normal(0., 1.)) เรียก tfd.Normal(0., 1.).log_prob สำหรับฟังก์ชั่นหลาม แต่ log_prob ร่องรอยโปรแกรมโดยใช้ JAX และรูปลักษณ์สำหรับงบการสุ่มตัวอย่าง log_prob การเปลี่ยนแปลงการทำงานในโปรแกรมส่วนใหญ่ที่ส่งกลับตัวแปรสุ่มโดยตรงหรือผ่านการแปลงผกผันได้ แต่ไม่ได้อยู่ในโปรแกรมที่ค่าตัวอย่างภายในที่ไม่ได้กลับมา หากไม่สามารถกลับการดำเนินงานที่จำเป็นในโปรแกรม log_prob จะโยนความผิดพลาด

นี่เป็นตัวอย่างของ log_prob นำไปใช้กับโปรแกรมต่างๆ

1. log_prob ทำงานบนโปรแกรมที่ตัวอย่างได้โดยตรงจากการกระจาย TFP (หรือลงทะเบียนประเภทอื่น ๆ ) และค่าตอบแทนของพวกเขา

def normal(key):
  return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))

-0.9189385

1. log_prob สามารถที่จะคำนวณการเข้าสู่ระบบความหนาแน่นของกลุ่มตัวอย่างจากโปรแกรมที่เปลี่ยน variates สุ่มโดยใช้ฟังก์ชั่น bijective (เช่น jnp.exp , jnp.tanh , jnp.split )

def log_normal(key):
  return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))

-1.159165

เพื่อคำนวณตัวอย่างจาก log_normal 's บันทึกความหนาแน่นเราต้องหมุนส่วน exp , การ log ของกลุ่มตัวอย่างที่แล้วเพิ่มการแก้ไขปริมาณการเปลี่ยนแปลงโดยใช้เข้าสู่ระบบเดชอุดมผกผันจาโคเบียนของ exp (ดู การเปลี่ยนแปลง ของตัวแปร สูตรจากวิกิพีเดีย)

1. log_prob ทำงานร่วมกับโปรแกรมที่โครงสร้างการส่งออกของกลุ่มตัวอย่างชอบพจนานุกรมหลามหรือ tuples

def normal_2d(key):
  x = random_variable(
    tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
  x1, x2 = jnp.split(x, 2, 0)
  return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))

{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546

1. log_prob เดินแบบของกราฟคำนวณโยงของฟังก์ชั่นการคำนวณค่าทั้งข้างหน้าและผกผัน (และเข้าสู่ระบบของพวกเขาเดชอุดม Jacobians) เมื่อมีความจำเป็นในการพยายามที่จะเชื่อมต่อค่ากลับมาพร้อมกับฐานค่าตัวอย่างของพวกเขาผ่านการเปลี่ยนแปลงที่ดีที่กำหนดของตัวแปร ใช้โปรแกรมตัวอย่างต่อไปนี้:

def complex_program(key):
  k1, k2 = random.split(key)
  z = random_variable(tfd.Normal(0., 1.))(k1)
  x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
  return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))

(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32))
-1.0967848

ในโปรแกรมนี้เราตัวอย่าง x เงื่อนไขใน z หมายถึงเราต้องค่าของ z ก่อนที่เราจะสามารถคำนวณการบันทึกความหนาแน่นของ x อย่างไรก็ตามในการสั่งซื้อเพื่อคำนวณ z อันดับแรกเราต้องหมุนส่วน jnp.exp นำไปใช้กับ z ดังนั้นเพื่อที่จะคำนวณการเข้าสู่ระบบความหนาแน่นของ x และ z , log_prob ความต้องการแรกกลับเอาท์พุทแรกแล้วผ่านมันไปข้างหน้าผ่าน jax.nn.relu ในการคำนวณค่าเฉลี่ย p(x | z)

สำหรับข้อมูลเพิ่มเติมเกี่ยว log_prob คุณสามารถอ้างถึง core.interpreters.log_prob ในการดำเนินการ, log_prob เป็นไปตามอย่างใกล้ชิดออกจาก inverse เปลี่ยนแปลง JAX; เพื่อเรียนรู้เพิ่มเติมเกี่ยวกับ inverse ดู core.interpreters.inverse

joint_sample

ในการกำหนดโปรแกรมที่ซับซ้อนและน่าสนใจยิ่งขึ้น เราจะใช้ตัวแปรสุ่มแฝงบางตัว เช่น ตัวแปรสุ่มที่มีค่าที่ไม่ได้สังเกต ลองมาดูที่ latent_normal โปรแกรมที่ตัวอย่างสุ่มค่า z ที่ใช้เป็นค่าเฉลี่ยของผู้อื่นค่าสุ่ม x

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

ในโปรแกรมนี้ z เพื่อให้แฝงถ้าเราจะเพียงโทร latent_normal(random.PRNGKey(0)) เราจะไม่ทราบว่าค่าที่แท้จริงของ z ที่มีหน้าที่รับผิดชอบในการสร้าง x

joint_sample คือการเปลี่ยนแปลงที่แปลงโปรแกรมลงในโปรแกรมอื่นที่ให้ผลตอบแทนพจนานุกรมชื่อสตริงการทำแผนที่ (แท็ก) เพื่อค่าของพวกเขา ในการทำงาน เราต้องแน่ใจว่าเราแท็กตัวแปรแฝงเพื่อให้แน่ใจว่าปรากฏในเอาต์พุตของฟังก์ชันที่แปลงแล้ว

joint_sample(latent_normal)(random.PRNGKey(0))

{'x': DeviceArray(0.01873656, dtype=float32),
 'z': DeviceArray(0.14389044, dtype=float32)}

โปรดทราบว่า joint_sample แปลงโปรแกรมลงในโปรแกรมอื่นว่ากลุ่มตัวอย่างร่วมกันจำหน่ายกว่าค่าที่ซ่อนเร้นของเราจึงยังสามารถแปลงมัน สำหรับอัลกอริธึม เช่น MCMC และ VI เป็นเรื่องปกติที่จะคำนวณความน่าจะเป็นของบันทึกของการแจกแจงร่วมซึ่งเป็นส่วนหนึ่งของขั้นตอนการอนุมาน log_prob(latent_normal) ไม่ทำงานเพราะต้อง marginalizing ออก z แต่เราสามารถใช้ log_prob(joint_sample(latent_normal))

print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))

-50.03529
-5049.535

เพราะนี่คือการดังกล่าวเป็นรูปแบบทั่วไป, Oryx ยังมี joint_log_prob การเปลี่ยนแปลงซึ่งเป็นเพียงองค์ประกอบของ log_prob และ joint_sample

print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))

-50.03529
-5049.535

block

block การเปลี่ยนแปลงใช้เวลาในโปรแกรมและลำดับของชื่อและส่งกลับโปรแกรมที่จะทำงานเหมือนกันยกเว้นว่าในแปลงปลายน้ำ (เช่น joint_sample ) ชื่อให้ถูกละเว้น ตัวอย่างของการที่ block เป็นประโยชน์คือการแปลงกระจายร่วมเป็นก่อนมากกว่าตัวแปรแฝงด้วย "บล็อก" ค่าตัวอย่างในโอกาส ตัวอย่างเช่นใช้ latent_normal แรกที่ดึง z ~ N(0, 1) แล้ว x | z ~ N(z, 1e-1) block(latent_normal, names=['x']) เป็นโปรแกรมที่ซ่อนที่ x ชื่อดังนั้นหากเราทำ joint_sample(block(latent_normal, names=['x'])) เราได้รับพจนานุกรมที่มีเพียง z ในนั้น .

blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))

{'z': DeviceArray(0.14389044, dtype=float32)}

intervene

intervene clobbers เปลี่ยนแปลงตัวอย่างในโปรแกรมน่าจะมีค่าจากภายนอก จะกลับไปเรา latent_normal โปรแกรมสมมติว่าเรามีความสนใจในการเรียกใช้โปรแกรมเดียวกัน แต่อยาก z ได้รับการแก้ไขไป 4. มากกว่าการเขียนโปรแกรมใหม่ที่เราสามารถใช้ intervene เพื่อแทนที่ค่าของ z

intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();

/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

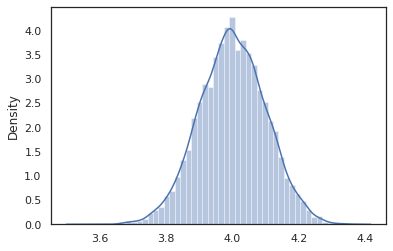
intervened ตัวอย่างฟังก์ชั่นจาก p(x | do(z = 4)) ซึ่งเป็นเพียงการแจกแจงแบบปกติมาตรฐานศูนย์กลางที่ 4. เมื่อเรา intervene ในค่าเฉพาะค่าที่ไม่ถือว่าเป็นตัวแปรสุ่ม ซึ่งหมายความว่า z มูลค่าจะไม่ถูกแท็กในขณะที่การดำเนินการ intervened

conditional

conditional การแปลงโปรแกรมที่แฝงตัวอย่างค่าเป็นหนึ่งที่เงื่อนไขค่าแฝงเหล่านั้น กลับมาที่เรา latent_normal โปรแกรมซึ่งตัวอย่าง p(x) กับแฝง z เราสามารถแปลงเป็นโปรแกรมที่มีเงื่อนไข p(x | z)

cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()

99.87485
49.874847
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

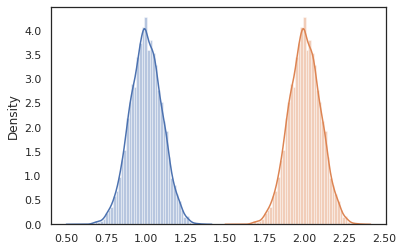
nest

เมื่อเราเริ่มเขียนโปรแกรมความน่าจะเป็นเพื่อสร้างโปรแกรมที่ซับซ้อนมากขึ้น เป็นเรื่องปกติที่จะนำฟังก์ชันที่มีตรรกะสำคัญมาใช้ซ้ำ ตัวอย่างเช่นถ้าเราต้องการที่จะสร้างเครือข่ายประสาทคชกรรมอาจจะมีความสำคัญ dense โปรแกรมที่น้ำหนักตัวอย่างและดำเนินการผ่านไปข้างหน้า

ถ้าเรานำมาใช้ฟังก์ชั่น แต่เราจะจบลงด้วยค่าติดแท็กที่ซ้ำกันในโปรแกรมสุดท้ายซึ่งไม่ได้รับอนุญาตโดยการแปลงเช่น joint_sample เราสามารถใช้ nest เพื่อสร้างแท็ก "ขอบเขต" ซึ่งตัวอย่างใด ๆ ที่อยู่ภายในขอบเขตที่ชื่อจะถูกแทรกลงในพจนานุกรมที่ซ้อนกัน

def f(key):
  return random_variable(tfd.Normal(0., 1.), name='x')(key)

def g(key):
  k1, k2 = random.split(key)
  return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))

{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
 'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }

กรณีศึกษา: โครงข่ายประสาทแบบเบย์

ลองมือของเราที่การฝึกอบรมเครือข่ายประสาทเบส์สำหรับแบ่งประเภทคลาสสิก ฟิชเชอร์ไอริส ชุด มันค่อนข้างเล็กและมีมิติต่ำ เราจึงสามารถลองสุ่มตัวอย่างส่วนหลังด้วย MCMC ได้โดยตรง

ก่อนอื่น มานำเข้าชุดข้อมูลและยูทิลิตี้เพิ่มเติมจาก Oryx กันก่อน

from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']

num_features = features.shape[-1]
num_classes = len(iris.target_names)

from oryx.experimental import mcmc
from oryx.util import summary, get_summaries

เราเริ่มต้นด้วยการใช้เลเยอร์ที่หนาแน่น ซึ่งจะมีลำดับความสำคัญปกติเหนือน้ำหนักและอคติ การทำเช่นนี้ครั้งแรกที่เรากำหนด dense ฟังก์ชั่นขั้นสูงที่ใช้เวลาในมิติที่ต้องการออกและฟังก์ชั่นการเปิดใช้งาน dense ฟังก์ชันส่งกลับน่าจะเป็นโปรแกรมที่แสดงถึงการกระจายเงื่อนไข p(h | x) ที่ h คือการส่งออกของชั้นหนาแน่นและ x เป็นปัจจัยการผลิต มันตัวอย่างแรกน้ำหนักและอคติแล้วใช้พวกเขาที่จะ x

def dense(dim_out, activation=jax.nn.relu):
  def forward(key, x):
    dim_in = x.shape[-1]
    w_key, b_key = random.split(key)
    w = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
          name='w')(w_key)
    b = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
          name='b')(b_key)
    return activation(jnp.dot(w, x) + b)
  return forward

การเขียนหลาย dense ชั้นด้วยกันเราจะดำเนินการ mlp (หลายตรอน) ฟังก์ชั่นการสั่งซื้อที่สูงขึ้นซึ่งจะใช้เวลาในรายการของขนาดที่ซ่อนอยู่และจำนวนของชั้นเรียน มันกลับโปรแกรมที่ซ้ำ ๆ เรียก dense โดยใช้ที่เหมาะสม hidden_size และในที่สุดก็จะส่งกลับ logits สำหรับแต่ละชั้นเรียนในชั้นสุดท้าย หมายเหตุการใช้งานของ nest ที่สร้างขอบเขตชื่อสำหรับแต่ละชั้น

def mlp(hidden_sizes, num_classes):
  num_hidden = len(hidden_sizes)
  def forward(key, x):
    keys = random.split(key, num_hidden + 1)
    for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
      x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
    logits = nest(dense(num_classes, activation=lambda x: x),
                  scope=f'layer_{num_hidden + 1}')(keys[-1], x)
    return logits
  return forward

ในการใช้โมเดลแบบเต็ม เราจำเป็นต้องสร้างโมเดลป้ายกำกับเป็นตัวแปรสุ่มตามหมวดหมู่ เราจะกำหนด predict ฟังก์ชั่นซึ่งจะใช้เวลาในชุดของ xs (คุณสมบัติ) ซึ่งจะผ่านไปแล้วเป็น mlp ใช้ vmap เมื่อเราใช้ vmap(partial(mlp, mlp_key)) เราลิ้มลองชุดเดียวของน้ำหนัก แต่ map ไปข้างหน้าผ่านเหนือทุกการป้อนข้อมูล xs นี้ผลิตชุดของ logits ซึ่ง parameterizes กระจายเด็ดขาดอิสระ

def predict(mlp):
  def forward(key, xs):
    mlp_key, label_key = random.split(key)
    logits = vmap(partial(mlp, mlp_key))(xs)
    return random_variable(
        tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
  return forward

นั่นคือรูปแบบเต็ม! ลองใช้ MCMC เพื่อสุ่มตัวอย่างส่วนหลังของน้ำหนัก BNN ที่ระบุ ครั้งแรกที่เราสร้าง BNN "แม่" โดยใช้ mlp

bnn = mlp([200, 200], num_classes)

เพื่อสร้างจุดเริ่มต้นสำหรับห่วงโซ่มาร์คอฟของเราเราสามารถใช้ joint_sample ด้วยการป้อนข้อมูลหุ่น

weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())

dict_keys(['layer_1', 'layer_2', 'layer_3'])

การคำนวณความน่าจะเป็นบันทึกการกระจายร่วมนั้นเพียงพอสำหรับอัลกอริธึมอนุมานจำนวนมาก ตอนนี้ขอบอกว่าเราสังเกต x และต้องการที่จะลิ้มลองหลัง p(z | x) สำหรับการกระจายซับซ้อนเราจะไม่สามารถที่จะเหยียดหยามออก x ( แต่สำหรับ latent_normal ที่เราสามารถทำได้) แต่เราสามารถคำนวณความหนาแน่นบันทึก unnormalized log p(z, x) ที่ x ได้รับการแก้ไขให้เป็นค่าโดยเฉพาะอย่างยิ่ง เราสามารถใช้ความน่าจะเป็นของบันทึกที่ไม่เป็นมาตรฐานกับ MCMC เพื่อสุ่มตัวอย่างหลัง มาเขียนฟังก์ชัน log prob ที่ "ถูกตรึง" กัน

def target_log_prob(weights):
  return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)

ตอนนี้เราสามารถใช้ tfp.mcmc ที่จะลิ้มลองหลังโดยใช้ฟังก์ชั่นความหนาแน่นบันทึก unnormalized ของเรา ทราบว่าเราจะต้องใช้ "บี้" รุ่นน้ำหนักซ้อนกันของเราในพจนานุกรมจะทำงานร่วมกับ tfp.mcmc ดังนั้นเราจึงใช้ JAX ของสาธารณูปโภคต้นไม้ให้เรียบและ unflatten

@jit
def run_chain(key, weights):
  flat_state, sample_tree = jax.tree_flatten(weights)

  def flat_log_prob(*states):
    return target_log_prob(jax.tree_unflatten(sample_tree, states))

  def trace_fn(_, results):
    return results.inner_results.accepted_results.target_log_prob

  flat_states, log_probs = tfp.mcmc.sample_chain(
    1000,
    num_burnin_steps=9000,
    kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
        tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
        9000, target_accept_prob=0.7),
    trace_fn=trace_fn,
    current_state=flat_state,
    seed=key)
  samples = jax.tree_unflatten(sample_tree, flat_states)
  return samples, log_probs
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)

plt.plot(log_probs)
plt.show()

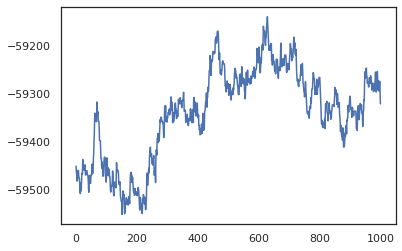
เราสามารถใช้ตัวอย่างของเราในการประมาณการแบบจำลองเฉลี่ยแบบเบย์ (BMA) ของความแม่นยำในการฝึกอบรม การคำนวณนั้นเราสามารถใช้ intervene กับ bnn การ "ฉีด" น้ำหนักหลังในสถานที่ของคนที่มีตัวอย่างจากที่สำคัญ การคำนวณ logits สำหรับแต่ละจุดข้อมูลสำหรับแต่ละตัวอย่างหลังเราสามารถดับเบิล vmap กว่า posterior_weights และ features

output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
    random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)

print('Average sample accuracy:', (
    output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
    output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())

Average sample accuracy: 0.9874067
BMA accuracy: 0.99333334

บทสรุป

ใน Oryx โปรแกรมความน่าจะเป็นเป็นเพียงฟังก์ชัน JAX ที่รับ (pseudo-) แบบสุ่มเป็นอินพุต เนื่องจากการบูรณาการอย่างแน่นหนาของ Oryx กับระบบการแปลงฟังก์ชันของ JAX เราจึงสามารถเขียนและจัดการโปรแกรมความน่าจะเป็นได้เหมือนกับเรากำลังเขียนโค้ด JAX ซึ่งส่งผลให้ระบบที่เรียบง่ายแต่ยืดหยุ่นสำหรับการสร้างแบบจำลองที่ซับซ้อนและการอนุมาน