 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
pip install -q -U jax jaxlibpip install -q -Uq oryx -Ipip install -q tfp-nightly --upgrade
from functools import partial
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')
import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
import oryx
Programowanie probabilistyczne to idea, w której możemy wyrazić modele probabilistyczne za pomocą funkcji z języka programowania. Zadania takie jak wnioskowanie bayesowskie lub marginalizacja są następnie dostarczane jako funkcje językowe i mogą być potencjalnie zautomatyzowane.
Oryx dostarcza probabilistyczny system programowania, w którym programy probabilistyczne są po prostu wyrażane jako funkcje Pythona; te programy są następnie przekształcane za pomocą przekształceń funkcji komponujących, takich jak te w JAX! Pomysł polega na tym, aby zacząć od prostych programów (takich jak próbkowanie z losowej normy) i skomponować je razem w celu utworzenia modeli (takich jak Bayesowska sieć neuronowa). Ważnym punktem Oryx za PPL projektu jest umożliwienie programy wyglądać funkcji wy mieliście już pisać i stosowania w JAX, ale są opatrzone dokonać przekształcenia ich świadomi.
Najpierw zaimportujmy podstawową funkcjonalność PPL Oryxa.
from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest
Czym są programy probabilistyczne w Oryxie?
W Oryxie programy probabilistyczne są po prostu czystymi funkcjami Pythona, które operują na wartościach JAX i kluczach pseudolosowych i zwracają losową próbkę. Zgodnie z projektem, są one zgodne z przekształceń jak jit i vmap . Jednak Oryx probabilistyczny system programowania dostarcza narzędzi, które pozwalają na opisywanie swoich funkcji przydatnych sposobów.
Po filozofii JAX czystych funkcji, program probabilistyczny Oryx jest funkcją Pythona, który zajmuje JAX PRNGKey jako pierwszy argument i dowolnej liczby kolejnych argumentów klimatyzacyjnych. Wyjście z funkcji jest nazywany „próbka” i te same ograniczenia, które odnoszą się do jit -ed i vmap funkcje -ed zastosowania do programów probabilistycznych (EG brak przepływu danych zależny od sterowania, bez skutków ubocznych, etc.). Różni się to od wielu imperatywnych probabilistycznych systemów programowania, w których „próbką” jest cały ślad wykonania, w tym wartości wewnętrzne dla wykonania programu. Zobaczymy później jak Oryx mogą uzyskać dostęp do wartości wewnętrznych za pomocą joint_sample , omówione poniżej.
Program :: PRNGKey -> ... -> Sample
Oto program „Hello World”, że próbki z rozkładu logarytmiczno-normalny .
def log_normal(key):
return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.) 0.8139614 /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
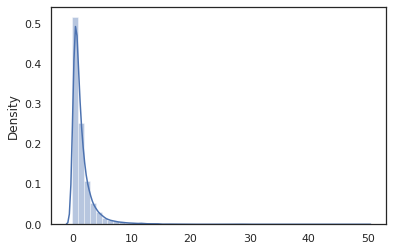
log_normal funkcja jest cienka owijka wokół Tensorflow Prawdopodobieństwo (TFP) dystrybucji, ale zamiast dzwonić tfd.Normal(0., 1.).sample , używaliśmy random_variable zamiast. Jak zobaczymy później, random_variable pozwala nam konwertować przedmiotów do programów probabilistycznych, wraz z innymi przydatnymi funkcjami.
Możemy konwertować log_normal do funkcji log gęstości przy użyciu log_prob transformację:
print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()
-0.9189385
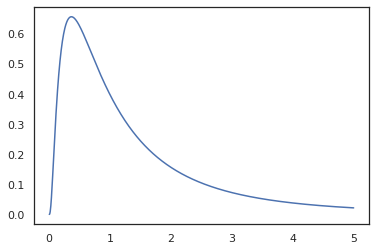
Ponieważ mamy odnotowany funkcji z random_variable , log_prob ma świadomość, że nie było wywołanie tfd.Normal(0., 1.).sample i wykorzystuje tfd.Normal(0., 1.).log_prob obliczyć dystrybucję bazową log prawd. Aby poradzić sobie z jnp.exp , ppl.log_prob automatycznie oblicza gęstość dzięki funkcji bijective, śledzenie zmian objętości w change-of-zmienna obliczeń.
W Oryx, możemy wziąć programów i przekształcić je za pomocą przekształceń funkcyjnych - np jax.jit lub log_prob . Oryx nie może tego zrobić za pomocą dowolnego programu; wymaga funkcji próbkowania, które zarejestrowały swoją funkcję gęstości dziennika w Oryxie. Na szczęście, Oryx automatycznie rejestruje TensorFlow Prawdopodobieństwo (TFP) rozkładów w swoim systemie.
Probabilistyczne narzędzia programowania Oryx
Oryx ma kilka transformacji funkcji ukierunkowanych na programowanie probabilistyczne. Omówimy większość z nich i podamy kilka przykładów. Na koniec połączymy to wszystko w studium przypadku MCMC. Można również zapoznać się z dokumentacją core.ppl.transformations więcej szczegółów.
random_variable
random_variable ma dwa główne elementy funkcjonalności, zarówno koncentruje się na opisywanie funkcji Pythona z informacji, które mogą być używane w transformacji.
random_variable'działa jak funkcja tożsamości domyślnie, ale można użyć specyficznego typu rejestracje obiektów przekształcić probabilistyczny programs.`Dla typów płatnych na żądanie (funkcje Python, lambda,
functools.partials, etc.) i arbitralneobjects (jak JAXDeviceArrays) będzie po prostu zwrócić swoje wejście.random_variable(x: object) == x random_variable(f: Callable[...]) == fOryx automatycznie rejestruje TensorFlow prawdopodobieństwa (TFP) dystrybucji, które są przekształcane probabilistycznych programów, które wywołują dystrybucji,
samplesposobu.random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235Oryx dodatkowo osadza informacje o dystrybucji TFP w śladach JAX, co umożliwia automatyczne obliczanie gęstości logów.
random_variablewartości zmiennych można z nazwami, co czyni je użytecznymi dla dalszych przekształceń, dostarczając opcjonalnąnameargumentu słowa kluczowego dorandom_variable. Gdy przekazuje się tablicę dorandom_variablewraz zname(nprandom_variable(x, name='x')), to właśnie znaczniki wartość i zwraca go. Jeśli mijamy w płatnych na żądanie lub dystrybucji TFP,random_variableZwraca programu, tagi próba wyjścia z jegoname.
Adnotacje te nie zmieniają semantyki programu po uruchomieniu, ale tylko wtedy, gdy przekształcone (czyli program powróci taką samą wartość z lub bez użycia random_variable ).
Przyjrzyjmy się przykładowi, w którym używamy obu elementów funkcjonalności razem.
def latent_normal(key):
z_key, x_key = random.split(key)
z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)
W tym programie mamy oznaczone pośrednich z i x , co sprawia, że transformacje joint_sample , intervene , conditional i graph_replace świadom nazw 'z' i 'x' . Później przyjrzymy się dokładnie, w jaki sposób każda transformacja używa nazw.
log_prob
log_prob transformacja funkcja konwertuje probabilistyczny programu Oryx do jego funkcji log gęstości. Ta funkcja gęstości logarytmicznej pobiera potencjalną próbkę z programu jako dane wejściowe i zwraca jej gęstość logarytmiczną w ramach podstawowego rozkładu próbkowania.
log_prob :: Program -> (Sample -> LogDensity)
Jak random_variable , działa za pośrednictwem rejestru typów gdzie dystrybucje TFP są automatycznie rejestrowane, więc log_prob(tfd.Normal(0., 1.)) zwraca tfd.Normal(0., 1.).log_prob . Dla funkcji Pythona, jednak log_prob ślady programu za pomocą JAX i szuka próbek oświadczenia. log_prob transformacja działa na większości programów, które zwracają zmienne losowe, bezpośrednio lub za pośrednictwem odwracalnych przemian, ale nie na programy, które wewnętrznie przykładowe wartości, które nie są zwracane. Jeśli nie można odwrócić niezbędnych czynności w programie, log_prob wygeneruje błąd.
Oto kilka przykładów log_prob stosowane do różnych programów.
-
log_probprace nad programami, które bezpośrednio próbki z rozkładów TFP (lub innych zarejestrowanych typów) i wrócić do swoich wartości.
def normal(key):
return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))
-0.9189385
-
log_probjest w stanie obliczyć dziennika-gęstości próbek z programów, które przekształcają losowych zmiennymi za pomocą funkcji bijective (npjnp.exp,jnp.tanh,jnp.split).
def log_normal(key):
return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))
-1.159165
W celu obliczenia próbki z log_normal „s dziennika gęstości, najpierw musimy odwrócić exp , biorąc log próbki, a następnie dodać korekcję objętości zmian za pomocą odwrotność log-det Jacobiego z exp (patrz zmiany zmiennej wzór ze Wikipedia).
-
log_probwspółpracuje z programami, które struktur wyjściowych próbkach podoba, słowniki Python lub krotki.
def normal_2d(key):
x = random_variable(
tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
x1, x2 = jnp.split(x, 2, 0)
return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))
{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546
-
log_probchodniki wyznaczoną wykres obliczaniu funkcji obliczania wartości zarówno do przodu i odwróconej (i ich Jacobians log-det), w razie potrzeby, starając się łączyć z ich zwróconych wartości bazowych próbkowanych wartości za pomocą dobrze określonej zmianie zmiennych. Weźmy następujący przykładowy program:
def complex_program(key):
k1, k2 = random.split(key)
z = random_variable(tfd.Normal(0., 1.))(k1)
x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))
(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32)) -1.0967848
W tym programie przykładowe x warunkowo na z , czyli musimy wartość z przed możemy obliczyć dziennik gęstość x . Jednakże, w celu obliczenia z , najpierw musimy odwrócić jnp.exp stosowane do z . Tak więc, w celu obliczenia logarytmu gęstości x i z , log_prob potrzeb najpierw inwertowany pierwszego wyjścia, a następnie przekazać je do przodu przez jax.nn.relu obliczyć średnią p(x | z) .
Aby uzyskać więcej informacji na temat log_prob , można zwrócić się do core.interpreters.log_prob . W realizacji, log_prob jest ściśle opiera się na inverse transformacji JAX; Aby dowiedzieć się więcej o inverse zobacz core.interpreters.inverse .
joint_sample
Aby zdefiniować bardziej złożone i interesujące programy, użyjemy ukrytych zmiennych losowych, tj. zmiennych losowych o nieobserwowanych wartościach. Załóżmy, odnoszą się do latent_normal programu, że próbki wartość losowa z , który jest używany jako średnią z innej losowej wartości x .
def latent_normal(key):
z_key, x_key = random.split(key)
z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)
W tym programie z jest ukryta tak, jakbyśmy byli po prostu zadzwonić latent_normal(random.PRNGKey(0)) nie wiedzielibyśmy rzeczywistą wartość z , który jest odpowiedzialny za generowanie x .
joint_sample jest transformacja, która przekształca program na inny program, który zwraca słownika mapowanie nazwy smyczkowe (tagi) do ich wartości. Aby działać, musimy się upewnić, że oznaczyliśmy ukryte zmienne, aby upewnić się, że pojawią się w wyniku przekształconej funkcji.
joint_sample(latent_normal)(random.PRNGKey(0))
{'x': DeviceArray(0.01873656, dtype=float32),
'z': DeviceArray(0.14389044, dtype=float32)}
Zauważ, że joint_sample przekształca program do innego programu, że próbki wspólna dystrybucja na jego ukrytych wartości, więc można dalej przekształcić go. W przypadku algorytmów, takich jak MCMC i VI, często oblicza się prawdopodobieństwo logarytmu łącznego rozkładu w ramach procedury wnioskowania. log_prob(latent_normal) nie działa, ponieważ wymaga się marginalizacji z , ale możemy użyć log_prob(joint_sample(latent_normal)) .
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))
-50.03529 -5049.535
Ponieważ jest to wspólny wzór, Oryx ma również joint_log_prob transformacji, która jest tylko kompozycja log_prob i joint_sample .
print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))
-50.03529 -5049.535
block
block transformacja trwa w programie i sekwencji nazw i zwraca program, który zachowuje się identycznie z wyjątkiem, że w dalszych przekształceniach (jak joint_sample ), przy czym przewidziane nazwy są ignorowane. Przykładem, w którym block jest przydatna jest konwersja wspólne rozmieszczenie w uprzednim ciągu ukrytych zmiennych przez „blokowanie” wartości próby prawdopodobieństwa. Na przykład, należy latent_normal , które początkowo wyciąga z ~ N(0, 1) wówczas x | z ~ N(z, 1e-1) . block(latent_normal, names=['x']) to program, który ukrywa x imię, więc jeśli zrobimy joint_sample(block(latent_normal, names=['x'])) , otrzymujemy słownik z tylko z w nim .
blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))
{'z': DeviceArray(0.14389044, dtype=float32)}
intervene
intervene próbek clobbers transformacji w probabilistyczny programu z wartościami z zewnątrz. Wracając do naszego latent_normal programu, powiedzmy, że byliśmy zainteresowani w prowadzeniu tego samego programu, ale chciał z do przymocowania do 4. Zamiast pisać nowy program, możemy użyć intervene , aby zastąpić wartość z .
intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
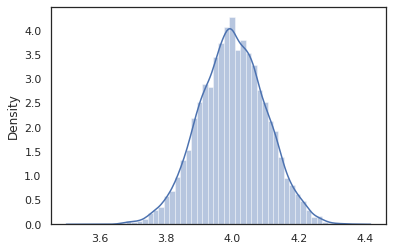
Do intervened próbki z funkcji p(x | do(z = 4)) , który jest po prostu standardowy rozkład normalny skupione na 4. Kiedy intervene na określonej wartości, wartość ta nie jest już uważana za zmienną losową. Oznacza to, że z wartości nie zostaną oznaczone podczas wykonywania intervened .
conditional
conditional przekształca program próbki utajonego wartości w jednym że warunki na tych wartościach utajonym. Wracając do naszego latent_normal programu, którego próbki p(x) z utajonym z , możemy przekształcić go w warunkowego programu p(x | z) .
cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()
99.87485 49.874847 /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning) /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
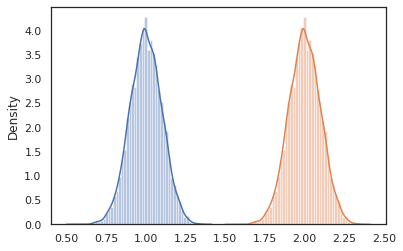
nest
Kiedy zaczynamy komponować programy probabilistyczne, aby budować bardziej złożone, często ponownie wykorzystujemy funkcje, które mają pewną ważną logikę. Na przykład, jeśli chcemy zbudować Bayesa sieci neuronowej, nie może być ważnym dense program próbki ciężary i wykonuje podanie do przodu.
Jeśli będziemy ponownie użyć funkcji, jednak możemy skończyć z podwójnych wartości oznaczane w ostatecznej wersji programu, która jest niedozwolone przez transformacje jak joint_sample . Możemy użyć nest stworzyć tag „zakresy”, gdzie wszelkie próbki wewnątrz nazwanego zakresu zostanie wstawiony do zagnieżdżonego słownika.
def f(key):
return random_variable(tfd.Normal(0., 1.), name='x')(key)
def g(key):
k1, k2 = random.split(key)
return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))
{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }
Studium przypadku: Bayesowska sieć neuronowa
Spróbujmy naszą rękę na treningu sieci neuronowej do klasyfikacji Bayesa klasyczne Fisher Iris zestaw danych. Jest stosunkowo mały i niskowymiarowy, więc możemy spróbować bezpośrednio pobrać próbkę tylną za pomocą MCMC.
Najpierw zaimportujmy zestaw danych i kilka dodatkowych narzędzi z Oryx.
from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
from oryx.experimental import mcmc
from oryx.util import summary, get_summaries
Zaczynamy od zaimplementowania gęstej warstwy, która będzie miała normalne a priori nad wagami i odchyleniem. Aby to zrobić, należy najpierw określić dense funkcja wyższego rzędu, które ma w żądanej funkcji wymiarów wyjściowego i aktywacji. dense zwraca probabilistyczny program oznacza warunkowego dystrybucji p(h | x) , gdzie h jest wyjście gęstej warstwy i x jest dane wejściowe. Najpierw próbki waga i stronniczości, a następnie stosuje je do x .
def dense(dim_out, activation=jax.nn.relu):
def forward(key, x):
dim_in = x.shape[-1]
w_key, b_key = random.split(key)
w = random_variable(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
name='w')(w_key)
b = random_variable(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
name='b')(b_key)
return activation(jnp.dot(w, x) + b)
return forward
Aby skomponować kilka dense warstw ze sobą, będziemy realizować mlp (perceptron wielowarstwowy), który zaczyna się na liście ukrytych wymiarów i liczby klas funkcja wyższego rzędu. Zwraca program, który wielokrotnie wywołuje dense stosując odpowiednią hidden_size i wreszcie powraca logits dla każdej klasy w ostatniej warstwie. Zwróć uwagę na użycie nest co stwarza nazw zakresów dla każdej warstwy.
def mlp(hidden_sizes, num_classes):
num_hidden = len(hidden_sizes)
def forward(key, x):
keys = random.split(key, num_hidden + 1)
for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
logits = nest(dense(num_classes, activation=lambda x: x),
scope=f'layer_{num_hidden + 1}')(keys[-1], x)
return logits
return forward
Aby zaimplementować pełny model, musimy zamodelować etykiety jako jakościowe zmienne losowe. Będziemy zdefiniować predict funkcję, która zaczyna się w zbiorze danych o xs (cech), które są następnie przekazywane do wiadomości mlp wykorzystaniem vmap . Gdy używamy vmap(partial(mlp, mlp_key)) , możemy spróbować jednego zestawu ciężarków, ale odwzorować podaniu nad wszystkimi wejściowych xs . W ten sposób powstaje zbiór logits który parametryzuje niezależnych rozkładów kategoryczne.
def predict(mlp):
def forward(key, xs):
mlp_key, label_key = random.split(key)
logits = vmap(partial(mlp, mlp_key))(xs)
return random_variable(
tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
return forward
To pełny model! Użyjmy MCMC do spróbkowania a posteriori wag BNN podanych danych; najpierw skonstruować BNN „szablonu” za pomocą mlp .
bnn = mlp([200, 200], num_classes)
Aby skonstruować punkt wyjścia dla naszego łańcucha Markowa, możemy użyć joint_sample z wejściem manekina.
weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())
dict_keys(['layer_1', 'layer_2', 'layer_3'])
Obliczenie łącznego prawdopodobieństwa logarytmicznego rozkładu jest wystarczające dla wielu algorytmów wnioskowania. Załóżmy teraz powiedzieć obserwujemy x i chcą spróbować tylną p(z | x) . W przypadku skomplikowanych rozkładów, nie będzie mógł się zmarginalizować x (choć dla latent_normal możemy), ale możemy obliczyć nieznormalizowanych gęstość log log p(z, x) , gdzie x jest przymocowany do określonej wartości. Możemy użyć nieznormalizowanego prawdopodobieństwa logarytmicznego z MCMC do próbkowania a posteriori. Napiszmy tę „przypiętą” funkcję log prob.
def target_log_prob(weights):
return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)
Teraz możemy użyć tfp.mcmc aby spróbować posterior używając naszej funkcji nieznormalizowanych gęstości dziennika. Należy pamiętać, że będziemy musieli użyć „spłaszczony” naszego słownika do zagnieżdżonych ciężarami być zgodne z tfp.mcmc , więc używamy narzędzia drzewo Jax, aby spłaszczyć i unflatten.
@jit
def run_chain(key, weights):
flat_state, sample_tree = jax.tree_flatten(weights)
def flat_log_prob(*states):
return target_log_prob(jax.tree_unflatten(sample_tree, states))
def trace_fn(_, results):
return results.inner_results.accepted_results.target_log_prob
flat_states, log_probs = tfp.mcmc.sample_chain(
1000,
num_burnin_steps=9000,
kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
9000, target_accept_prob=0.7),
trace_fn=trace_fn,
current_state=flat_state,
seed=key)
samples = jax.tree_unflatten(sample_tree, flat_states)
return samples, log_probs
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)
plt.plot(log_probs)
plt.show()
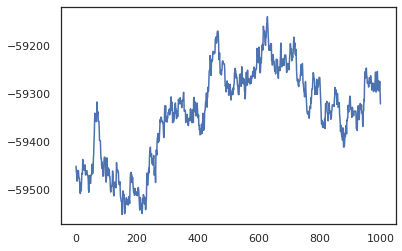
Możemy użyć naszych próbek, aby oszacować uśrednienie modelu bayesowskiego (BMA) dokładności uczenia. Aby obliczyć go, możemy użyć intervene z bnn „wstrzyknięcie” tylnego ciężarami w miejsce tych, które zostały pobrane z kluczem. Aby obliczyć logits dla każdego punktu danych dla każdej próbki tylnej, możemy podwoić vmap nad posterior_weights i features .
output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)
print('Average sample accuracy:', (
output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())
Average sample accuracy: 0.9874067 BMA accuracy: 0.99333334
Wniosek
W Oryxie programy probabilistyczne są po prostu funkcjami JAX, które przyjmują (pseudo-)losowość jako dane wejściowe. Ze względu na ścisłą integrację Oryxa z systemem transformacji funkcji JAX, możemy pisać i manipulować programami probabilistycznymi, tak jak piszemy kod JAX. Skutkuje to prostym, ale elastycznym systemem do budowania złożonych modeli i wnioskowania.
