Oryx의 확률 프로그래밍

TensorFlow.org에서 보기

Google Colab에서 실행

GitHub에서 소스 보기

노트북 다운로드

pip install -q -U jax jaxlib
pip install -q -Uq oryx -I
pip install -q tfp-nightly --upgrade

from functools import partial

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')

import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random

from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions

import oryx

확률 프로그래밍은 프로그래밍 언어의 기능을 사용하여 확률 모델을 표현할 수 있다는 아이디어입니다. 베이지안 추론 또는 주변화와 같은 작업은 언어 기능으로 제공되며 잠재적으로 자동화될 수 있습니다.

Oryx는 확률적 프로그램이 파이썬 함수로 표현되는 확률적 프로그래밍 시스템을 제공합니다. 그런 다음 이러한 프로그램은 JAX에서와 같이 구성 가능한 함수 변환을 통해 변환됩니다! 아이디어는 (임의의 법선에서 샘플링과 같은) 간단한 프로그램으로 시작하여 함께 구성하여 모델을 형성하는 것입니다(예: 베이지안 신경망). 오릭스의 PPL 디자인의 중요한 점은 JAX에서 이미 쓸 줄 기능과 사용처럼 보이도록 프로그램을 활성화하는 것입니다,하지만 그들 중 변환을 알리기 위해 주석이 있습니다.

먼저 Oryx의 핵심 PPL 기능을 가져오겠습니다.

from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest

Oryx에서 확률 프로그램이란 무엇입니까?

Oryx에서 확률 프로그램은 JAX 값과 의사 난수 키에서 작동하고 임의의 샘플을 반환하는 순수한 Python 함수입니다. 디자인함으로써, 그들은 같은 변환과 호환되는 jit 및 vmap . 그러나, 오릭스 확률 프로그래밍 시스템은 유용한 방법으로 기능을 주석 할 수 있도록 도구를 제공합니다.

순수한 함수 JAX 철학 이어 오릭스 확률 프로그램은 JAX 얻어 파이썬 함수 PRNGKey 첫 번째 인자 및 후속 조절 인자의 수있다. 이 함수의 출력은 "샘플"및 적용 동일한 제한이라고 jit -ed 및 vmap -ed 함수 확률 프로그램 (예 아니오 데이터 의존 제어 흐름 부작용 등)에 적용된다. 이것은 '샘플'이 프로그램 실행 내부 값을 포함하는 전체 실행 추적인 많은 명령형 확률 프로그래밍 시스템과 다릅니다. 우리는 오릭스가 사용하는 내부 값에 액세스 할 수있는 방법을 나중에 볼 수 joint_sample 아래에 설명을.

Program :: PRNGKey -> ... -> Sample

여기에 "안녕 세계"프로그램이된다는에서 샘플 로그 정규 분포 .

def log_normal(key):
  return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))

print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
0.8139614
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

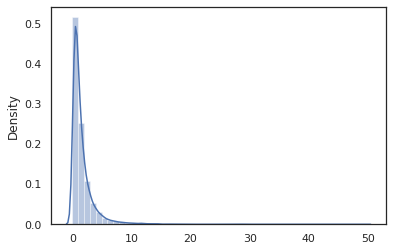
log_normal 기능은 주위에 얇은 래퍼입니다 Tensorflow 확률 (TFP) 대신 호출, 유통 tfd.Normal(0., 1.).sample , 우리가 사용했던 random_variable 대신. 우리가 나중에 살펴 보 겠지만, random_variable 다른 유용한 기능과 함께 확률 프로그램에 객체를 변환하는 우리를 할 수 있습니다.

우리는 변환 할 수 있습니다 log_normal 사용하여 로그 - 밀도 함수에 log_prob 변화를 :

print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()

-0.9189385

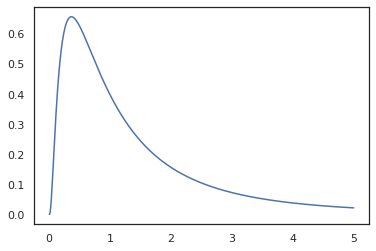
우리가 가진 기능 주석했기 때문에 random_variable , log_prob 에 대한 호출이 있었다는 것을 알고있다 tfd.Normal(0., 1.).sample 및 사용 tfd.Normal(0., 1.).log_prob 기본 분포를 계산하기 위해 로그 문제 핸들하려면 jnp.exp , ppl.log_prob 자동으로 변화의 계산에 가변 볼륨 변경을 추적, 전단 사 함수를 통해 밀도를 계산한다.

오릭스, 우리는 프로그램을 취할 수와 기능 변환을 사용하여 변환 - 예, 대한 jax.jit 또는 log_prob . Oryx는 어떤 프로그램으로도 이것을 할 수 없습니다. Oryx에 로그 밀도 함수를 등록한 샘플링 함수가 필요합니다. 다행히도, 영양 자동 등록 TensorFlow 확률 의 시스템 (TFP) 분포.

Oryx의 확률적 프로그래밍 도구

Oryx는 확률적 프로그래밍에 맞춰진 몇 가지 함수 변환을 가지고 있습니다. 우리는 그들 대부분을 살펴보고 몇 가지 예를 제공할 것입니다. 마지막으로 이 모든 것을 MCMC 사례 연구에 통합할 것입니다. 당신은 또한에 대한 설명서를 참조 할 수 있습니다 core.ppl.transformations 자세한 내용은.

random_variable

random_variable 기능의 두 개의 주요 부분을 가지고, 양쪽의 변환에 사용할 수있는 정보와 파이썬 주석 기능에 초점을 맞추었다.

1. random_variable '기본적으로 신원 기능으로 작동하지만 확률 programs.`로 변환 객체 타입 별 등록을 사용할 수 있습니다

   호출 유형 (파이썬 함수 람다 대해서는 functools.partial S 등), 임의의 object 들 (JAX 등 DeviceArray 들)는 단지 그것의 입력을 반환한다.

   random_variable(x: object) == x
   random_variable(f: Callable[...]) == f
   

   영양 자동 등록 TensorFlow 확률 (TFP) 분포의 확률 호출 프로그램으로 변환 분포 sample 방법.

   random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235
   

   Oryx는 로그 밀도를 자동으로 계산할 수 있는 JAX 추적에 TFP 배포에 대한 정보를 추가로 포함합니다.

2. random_variable 이름 캔 태그 값, 옵션으로 제공함으로써, 다운 스트림 변환하기에 유용하게 name 에 키워드 인수 random_variable . 우리는에 배열을 전달하는 경우 random_variable 과 함께 name (예를 들어 random_variable(x, name='x') ), 그냥 가치와 수익률을 태그. 우리가 호출 또는 TFP 분배에 전달하면 random_variable 반환 프로그램과 태그의 출력 샘플 그 name .

실행될 때, 이러한 통계는 프로그램의 의미를 변경하지 않지만, 변환 된 경우에만 (즉,이 프로그램을 사용하거나 사용하지 않고 동일 값을 반환 random_variable ).

두 가지 기능을 함께 사용하는 예를 살펴보겠습니다.

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

이 프로그램에서 우리는 중간에 태그를 추가 한 z 와 x 변형에 만들고, joint_sample , intervene , conditional 및 graph_replace 이름을 알고 'z' 와 'x' . 나중에 각 변환이 이름을 사용하는 방법을 정확히 살펴보겠습니다.

log_prob

log_prob 기능 변화는 로그 밀도 함수로의 영양 확률 프로그램을 변환한다. 이 로그 밀도 함수는 프로그램에서 잠재적인 샘플을 입력으로 사용하고 기본 샘플링 분포에서 로그 밀도를 반환합니다.

log_prob :: Program -> (Sample -> LogDensity)

마찬가지로 random_variable , 너무, 총요소 생산성 분포가 자동으로 등록되는 유형의 레지스트리를 통해 작동 log_prob(tfd.Normal(0., 1.)) 를 호출 tfd.Normal(0., 1.).log_prob . 파이썬 함수의 경우, 그러나, log_prob 문을 샘플링 JAX과 외모를 사용하여 프로그램을 추적합니다. log_prob 변환은 확률 변수를 반환 대부분의 프로그램, 직접 또는 가역 변환을 통하여하지만 프로그램에 대한 샘플 값은 내부적으로 반환되지 않은 것을에서 작동합니다. 이 프로그램에 필요한 작업을 반전 할 수없는 경우, log_prob 오류가 발생합니다.

다음의 몇 가지 예입니다 log_prob 다양한 프로그램에 적용이.

1. log_prob 직접 TFP 분포 (또는 등록 된 다른 종류)의 샘플과 자신의 값을 반환 프로그램에서 작동합니다.

def normal(key):
  return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))

-0.9189385

1. log_prob (예를 들어, 전단 사 함수를 사용하여 임의 variates 변환 프로그램에서 샘플 로그 밀도를 계산할 수있다 jnp.exp , jnp.tanh , jnp.split ).

def log_normal(key):
  return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))

-1.159165

발 시료 계산하기 위해 log_normal S '을 기록 밀도 우리 반전 먼저 필요 exp 상기 촬영 log 역 로그 DET 자코비하여 체적 변화 보정을 추가 한 다음 샘플을, 그리고 exp 투시 ( 변경 변수 위키 화학식에서).

1. log_prob 프로그램과 작품의 샘플 출력 구조는 파이썬 사전 또는 튜플을 좋아하는.

def normal_2d(key):
  x = random_variable(
    tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
  x1, x2 = jnp.split(x, 2, 0)
  return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))

{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546

1. log_prob 순방향 및 역 값을 계산하는 함수의 추적 계산 그래프 안내 (및 로그 DET 코비안) 필요한 변수의 잘 정의 된 변화를 통해 그들의 기본 샘플링 값으로 리턴 값을 연결을 시도한다. 다음 예제 프로그램을 사용하십시오.

def complex_program(key):
  k1, k2 = random.split(key)
  z = random_variable(tfd.Normal(0., 1.))(k1)
  x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
  return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))

(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32))
-1.0967848

이 프로그램에서는 샘플 x 조건에 z 우리 의미는 필요한 값 z 우리의 기록 밀도를 계산하기 전에 x . 그러나, 계산하기 위해 z , 먼저 반전 할 jnp.exp 인가 z . 따라서, 로그의 밀도를 계산하기 위해, x 및 z , log_prob 제 1 출력 전환 제에 요구하고 앞으로 전달할 jax.nn.relu 평균 계산하는 p(x | z) .

에 대한 자세한 내용은 log_prob , 당신은 참조 할 수 있습니다 core.interpreters.log_prob . 실시 예에서, log_prob 밀접의 오프 기반 inverse JAX 변환; 에 대해 더 배우고 inverse 참조 core.interpreters.inverse .

joint_sample

더 복잡하고 흥미로운 프로그램을 정의하기 위해 일부 잠재 확률 변수, 즉 관찰되지 않은 값이 있는 확률 변수를 사용합니다. 의가 참조하자 latent_normal 프로그램이 임의의 샘플 값 z 다른 랜덤 값의 평균으로서 사용되는 x .

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

이 프로그램에서, z 우리가 호출된다면 잠상 그렇다 latent_normal(random.PRNGKey(0)) 우리의 실제 값을 모를 것이다 z 생성을 담당 x .

joint_sample 변환입니다 다른 프로그램으로 변환하는 프로그램을 그 자신의 값으로 돌아갑니다 사전 매핑 문자열 이름 (태그). 작동하려면 변환된 함수의 출력에 표시되도록 잠재 변수에 태그를 지정해야 합니다.

joint_sample(latent_normal)(random.PRNGKey(0))

{'x': DeviceArray(0.01873656, dtype=float32),
 'z': DeviceArray(0.14389044, dtype=float32)}

참고 joint_sample 변환이 다른 프로그램에 프로그램 샘플의 잠재 값 위에 조인트 분포하고 있으므로 추가로 변형시킬 수있다. MCMC 및 VI와 같은 알고리즘의 경우 추론 절차의 일부로 관절 분포의 로그 확률을 계산하는 것이 일반적입니다. log_prob(latent_normal) 가 밖으로 주 변화가 필요하기 때문에 작동하지 않습니다 z 하지만, 우리가 사용할 수 있습니다 log_prob(joint_sample(latent_normal)) .

print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))

-50.03529
-5049.535

이 같은 공통 패턴이므로, 영양도 갖는다 joint_log_prob 단 조성 및 변형 log_prob 및 joint_sample .

print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))

-50.03529
-5049.535

block

block 변환은 프로그램 이름의 순서와 동일하게 얻어 하향 변환 (같은 것을 제외하고 그 행동한다 프로그램 리턴 joint_sample ) 제공된 이름을 무시한다. 여기서의 예는 block 편리 우도 샘플링 "차단"값으로 잠재 변수 위에 이전에 공동 분포로 변환된다. 예를 들어, 소요 latent_normal 먼저 무하는 z ~ N(0, 1) 다음 x | z ~ N(z, 1e-1) . block(latent_normal, names=['x']) 수피가있는 프로그램 x 이름, 우리가 그렇다면 joint_sample(block(latent_normal, names=['x'])) , 우리가 가진 사전 구하는 z 그것에는 .

blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))

{'z': DeviceArray(0.14389044, dtype=float32)}

intervene

가 intervene 외부로부터 값을 갖는 확률 과정에서 변태 쳤을 샘플. 우리 다시 간다 latent_normal 프로그램을의 우리가 같은 프로그램을 실행에 관심이 있지만, 원 가정 해 봅시다 z 새로운 프로그램을 작성하는 것보다 4 대신에 고정되는, 우리가 사용할 수있는 intervene 의 값 오버라이드 (override) z .

intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();

/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

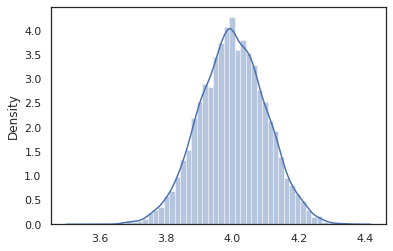
intervened 에서 함수의 샘플 p(x | do(z = 4)) 우리 때 단지 표준 정규 분포 4. 중심 인 intervene 의 특정 값은, 그 값이 더 이상 임의의 변수로 간주된다. A 본 방법 z 값하면서 태그되지 실행이 intervened .

conditional

conditional 변환 샘플 값을 하나로 잠재하고있는 프로그램이 그 값에 잠열 조건. 우리로 돌아 latent_normal 프로그램, 샘플 p(x) 잠재적으로 z , 우리는 조건부 프로그램으로 변환 할 수 있습니다 p(x | z) .

cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
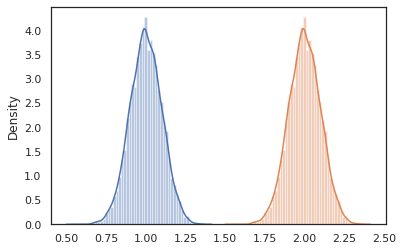
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()

99.87485
49.874847
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

nest

더 복잡한 프로그램을 만들기 위해 확률적 프로그램을 작성하기 시작할 때 몇 가지 중요한 논리가 있는 함수를 재사용하는 것이 일반적입니다. 우리는 베이지안 신경 네트워크를 구축하려는 경우 예를 들어, 중요한있을 수 있습니다 dense 프로그램 샘플 무게와가 실행이 앞으로 패스 그.

우리가 기능을 다시 사용하는 경우, 그러나, 우리는 같은 변환에 의해 허용되는 마지막 프로그램에서 중복 태그 값으로 끝낼 수 있습니다 joint_sample . 우리가 사용할 수있는 nest 태그를 생성하기 위해 명명 된 범위의 내부에 샘플이 중첩 사전에 삽입 될 위치를 "스코프".

def f(key):
  return random_variable(tfd.Normal(0., 1.), name='x')(key)

def g(key):
  k1, k2 = random.split(key)
  return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))

{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
 'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }

사례 연구: 베이지안 신경망

하자는 고전적인 분류에 대한 베이지안 신경망 훈련에 우리의 손을 시도 피셔 아이리스 데이터 집합을. 상대적으로 작고 저차원이므로 MCMC로 직접 후방 샘플링을 시도할 수 있습니다.

먼저 Oryx에서 데이터세트와 몇 가지 추가 유틸리티를 가져오겠습니다.

from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']

num_features = features.shape[-1]
num_classes = len(iris.target_names)

from oryx.experimental import mcmc
from oryx.util import summary, get_summaries

우리는 가중치와 편향에 대해 정상적인 우선순위를 갖는 조밀한 계층을 구현하는 것으로 시작합니다. 이를 위해, 우리는 먼저 정의 dense 원하는 출력 크기 및 활성화 기능에 소요 고차 기능을. dense 함수는 조건부 분포 나타내는 확률 프로그램 반환 p(h | x) h 치밀한 층의 출력이고, x 는 입력이다. 다음 첫 샘플 중량 바이어스 및 그들을 적용 x .

def dense(dim_out, activation=jax.nn.relu):
  def forward(key, x):
    dim_in = x.shape[-1]
    w_key, b_key = random.split(key)
    w = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
          name='w')(w_key)
    b = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
          name='b')(b_key)
    return activation(jnp.dot(w, x) + b)
  return forward

여러 작성하려면 dense 함께 층을, 우리는 구현합니다 mlp 숨겨진 크기의 목록 및 클래스의 수에 소요 (다층 퍼셉트론) 고차 기능을. 그것은 반복적으로 호출하는 프로그램 반환 dense 적절한 사용 hidden_size 마지막으로 최종 계층의 각 클래스에 대한 logits을 반환합니다. 사용주의 nest 각 레이어에 대한 이름 범위를 만듭니다.

def mlp(hidden_sizes, num_classes):
  num_hidden = len(hidden_sizes)
  def forward(key, x):
    keys = random.split(key, num_hidden + 1)
    for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
      x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
    logits = nest(dense(num_classes, activation=lambda x: x),
                  scope=f'layer_{num_hidden + 1}')(keys[-1], x)
    return logits
  return forward

전체 모델을 구현하려면 레이블을 범주형 확률 변수로 모델링해야 합니다. 우리는 정의됩니다 predict 의 데이터 세트에서 소요 기능 xs 다음에 전달된다 (기능) mlp 사용 vmap . 우리가 사용하는 경우 vmap(partial(mlp, mlp_key)) , 우리는 무게의 단일 세트 샘플 만 입력 온통 전방 패스지도 xs . 이것은 일련의 생산 logits 독립적 범주 분포 매개 변수화.

def predict(mlp):
  def forward(key, xs):
    mlp_key, label_key = random.split(key)
    logits = vmap(partial(mlp, mlp_key))(xs)
    return random_variable(
        tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
  return forward

풀모델입니다! MCMC를 사용하여 주어진 데이터에서 BNN 가중치의 사후를 샘플링해 보겠습니다. 우리는 먼저 사용 BNN "템플릿"을 구성 mlp .

bnn = mlp([200, 200], num_classes)

우리의 마르코프 체인의 시작 지점을 구축하기 위해 사용할 수 있습니다 joint_sample 더미 입력을.

weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())

dict_keys(['layer_1', 'layer_2', 'layer_3'])

많은 추론 알고리즘에 대해 공동 분포 로그 확률을 계산하는 것으로 충분합니다. 의 지금 우리가 관찰 해 봅시다 x 하고 후방 샘플링 할 p(z | x) . 복잡한 분포를 들어, 아웃 배척 할 수없는 것 x (위한 비록 latent_normal 하지만 수) 우리가 표준화 로그 농도 계산할 수 log p(z, x) x 는 특정 값으로 고정된다. MCMC와 함께 정규화되지 않은 로그 확률을 사용하여 사후 표본을 추출할 수 있습니다. 이 "고정된" 로그 prob 함수를 작성해 보겠습니다.

def target_log_prob(weights):
  return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)

이제 우리는 사용할 수 tfp.mcmc 우리의 표준화 로그 밀도 함수를 사용하여 후방을 샘플링 할 수 있습니다. 우리는 우리의 중첩 된 무게의 "평평"버전을 사용해야합니다 것을 참고와 호환되도록 사전을 tfp.mcmc 우리가 평평하고 패턴 화 해제하는 JAX의 나무 유틸리티를 사용하므로.

@jit
def run_chain(key, weights):
  flat_state, sample_tree = jax.tree_flatten(weights)

  def flat_log_prob(*states):
    return target_log_prob(jax.tree_unflatten(sample_tree, states))

  def trace_fn(_, results):
    return results.inner_results.accepted_results.target_log_prob

  flat_states, log_probs = tfp.mcmc.sample_chain(
    1000,
    num_burnin_steps=9000,
    kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
        tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
        9000, target_accept_prob=0.7),
    trace_fn=trace_fn,
    current_state=flat_state,
    seed=key)
  samples = jax.tree_unflatten(sample_tree, flat_states)
  return samples, log_probs
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)

plt.plot(log_probs)
plt.show()

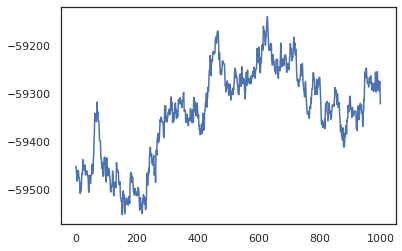
샘플을 사용하여 훈련 정확도의 베이지안 모델 평균화(BMA) 추정을 할 수 있습니다. 를 계산하기 위해 사용할 수있는 intervene 과 bnn 키에서 샘플링하는 것 대신에 "주입"후방 무게에. 각 후방 샘플에 대한 각 데이터 포인트에 대한 logits을 계산하기 위해, 우리는 두 배로 vmap 를 통해 posterior_weights 및 features .

output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
    random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)

print('Average sample accuracy:', (
    output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
    output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())

Average sample accuracy: 0.9874067
BMA accuracy: 0.99333334

결론

Oryx에서 확률적 프로그램은 입력으로 (의사)무작위를 취하는 JAX 함수일 뿐입니다. Oryx는 JAX의 함수 변환 시스템과 긴밀하게 통합되어 있기 때문에 JAX 코드를 작성하는 것처럼 확률적 프로그램을 작성하고 조작할 수 있습니다. 그 결과 복잡한 모델을 구축하고 추론을 수행하기 위한 간단하지만 유연한 시스템이 생성됩니다.