Oryx . में संभाव्य प्रोग्रामिंग

TensorFlow.org पर देखें

Google Colab में चलाएं

GitHub पर स्रोत देखें

नोटबुक डाउनलोड करें

pip install -q -U jax jaxlib
pip install -q -Uq oryx -I
pip install -q tfp-nightly --upgrade

from functools import partial

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')

import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random

from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions

import oryx

संभाव्य प्रोग्रामिंग यह विचार है कि हम प्रोग्रामिंग भाषा से सुविधाओं का उपयोग करके संभाव्य मॉडल व्यक्त कर सकते हैं। बायेसियन इंट्रेंस या हाशिए पर जाने जैसे कार्य तब भाषा सुविधाओं के रूप में प्रदान किए जाते हैं और संभावित रूप से स्वचालित हो सकते हैं।

ओरिक्स एक संभाव्य प्रोग्रामिंग प्रणाली प्रदान करता है जिसमें संभाव्य कार्यक्रमों को सिर्फ पायथन कार्यों के रूप में व्यक्त किया जाता है; इन प्रोग्रामों को तब JAX की तरह कंपोज़ेबल फंक्शन ट्रांसफ़ॉर्मेशन के माध्यम से रूपांतरित किया जाता है! विचार सरल कार्यक्रमों के साथ शुरू करना है (जैसे यादृच्छिक सामान्य से नमूना लेना) और मॉडल बनाने के लिए उन्हें एक साथ बनाना (जैसे बायेसियन न्यूरल नेटवर्क)। ओरिक्स के पीपीएल डिजाइन का एक महत्वपूर्ण बिंदु कार्यों आप पहले से ही लिखते हैं और JAX में उपयोग की तरह लग रहे करने के लिए कार्यक्रमों को सक्षम करने के लिए है, लेकिन परिवर्तनों उन्हें के बारे में पता करने के लिए एनोटेट कर रहे हैं।

आइए पहले ओरीक्स की कोर पीपीएल कार्यक्षमता को आयात करें।

from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest

ओरिक्स में संभाव्य कार्यक्रम क्या हैं?

ओरिक्स में, संभाव्य कार्यक्रम केवल शुद्ध पायथन फ़ंक्शन हैं जो JAX मानों और छद्म यादृच्छिक कुंजियों पर काम करते हैं और एक यादृच्छिक नमूना लौटाते हैं। डिजाइन करके, वे की तरह परिवर्तनों के साथ संगत कर रहे हैं jit और vmap । हालांकि, ओरिक्स संभाव्य प्रोग्रामिंग प्रणाली उपकरण है कि आप उपयोगी तरीकों से अपने कार्यों पर टिप्पणी करने के लिए सक्षम प्रदान करता है।

शुद्ध कार्यों का JAX दर्शन के बाद, एक ओरिक्स संभाव्य कार्यक्रम एक अजगर समारोह है कि एक JAX लेता है PRNGKey अपनी पहली तर्क और बाद कंडीशनिंग तर्क के किसी भी संख्या के रूप में। समारोह के उत्पादन में एक "नमूना" और एक ही प्रतिबंध है कि करने के लिए आवेदन कहा जाता है jit एड और vmap एड कार्यों संभाव्य कार्यक्रमों (जैसे कोई डेटा पर निर्भर नियंत्रण प्रवाह, कोई साइड इफेक्ट, आदि) के लिए लागू होते हैं। यह कई अनिवार्य संभाव्य प्रोग्रामिंग सिस्टम से अलग है जिसमें एक 'नमूना' संपूर्ण निष्पादन ट्रेस है, जिसमें प्रोग्राम के निष्पादन के लिए आंतरिक मान शामिल हैं। हम बाद में देखेंगे कैसे ओरिक्स का उपयोग कर आंतरिक मूल्यों का उपयोग कर सकते joint_sample , नीचे चर्चा की।

Program :: PRNGKey -> ... -> Sample

यहाँ एक "हैलो दुनिया" कार्यक्रम है कि एक से नमूने लॉग-सामान्य वितरण ।

def log_normal(key):
  return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))

print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
0.8139614
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

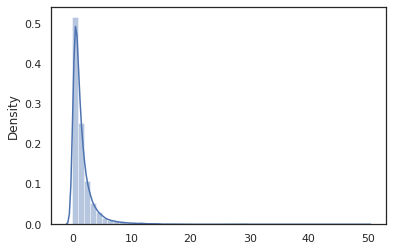
log_normal समारोह एक चारों ओर एक पतली आवरण है Tensorflow संभावना (टीएफपी) वितरण, लेकिन इसके बजाय बुलाने की tfd.Normal(0., 1.).sample , हम का उपयोग किया है random_variable बजाय। हम बाद में देखेंगे, random_variable संभाव्य कार्यक्रमों में वस्तुओं कन्वर्ट करने के लिए, अन्य उपयोगी कार्यक्षमता के साथ-साथ हमें सक्षम बनाता है।

हम में बदल सकते हैं log_normal का उपयोग कर एक लॉग-घनत्व समारोह में log_prob परिवर्तन:

print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()

-0.9189385

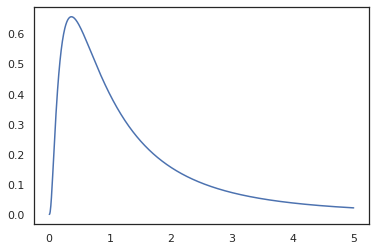
क्योंकि हम साथ समारोह एनोटेट गए random_variable , log_prob के लिए एक कॉल किया कि बारे में पता है tfd.Normal(0., 1.).sample और उपयोग करता tfd.Normal(0., 1.).log_prob आधार वितरण की गणना करने के लॉग प्रोब। संभाल करने jnp.exp , ppl.log_prob स्वचालित रूप से घनत्व द्विभाजित कार्यों के माध्यम से, गणना करता परिवर्तन के- चर गणना में मात्रा परिवर्तन का ट्रैक रखने के।

ओरिक्स में, हम कार्यक्रमों लेने के लिए और समारोह परिवर्तनों का उपयोग कर उन्हें बदल सकता है - उदाहरण के लिए, के लिए jax.jit या log_prob । हालांकि ओरिक्स किसी भी प्रोग्राम के साथ ऐसा नहीं कर सकता; इसके लिए नमूना कार्यों की आवश्यकता होती है जिन्होंने ओरीक्स के साथ अपने लॉग घनत्व फ़ंक्शन को पंजीकृत किया है। सौभाग्य से, ओरिक्स स्वचालित रूप से पंजीकृत करता TensorFlow संभावना अपने सिस्टम में (टीएफपी) वितरण।

ओरिक्स के संभाव्य प्रोग्रामिंग टूल

Oryx में संभाव्य प्रोग्रामिंग की दिशा में तैयार किए गए कई फ़ंक्शन ट्रांसफ़ॉर्मेशन हैं। हम उनमें से अधिकतर पर विचार करेंगे और कुछ उदाहरण प्रदान करेंगे। अंत में, हम इसे एमसीएमसी केस स्टडी में एक साथ रखेंगे। तुम भी के लिए दस्तावेज़ का उल्लेख कर सकते core.ppl.transformations अधिक जानकारी के लिए।

random_variable

random_variable कार्यक्षमता के दो मुख्य टुकड़े है, दोनों जानकारी है कि परिवर्तनों में इस्तेमाल किया जा सकता है के साथ अजगर कार्यों व्याख्या पर जोर दिया।

1. random_variable 'डिफ़ॉल्ट रूप से पहचान समारोह के रूप में चल रही है, लेकिन संभाव्य programs.` में तब्दील वस्तुओं के लिए विशेष प्रकार के पंजीकरण का उपयोग कर सकते

   प्रतिदेय प्रकार (अजगर काम करता है, lambdas, के लिए functools.partial रों, आदि) और मनमाना object है (जैसे JAX DeviceArray रों) यह सिर्फ अपने इनपुट वापस आ जाएगी।

   random_variable(x: object) == x
   random_variable(f: Callable[...]) == f
   

   ओरिक्स स्वचालित रूप से पंजीकृत करता TensorFlow संभावना (टीएफपी) वितरण, जो संभाव्य प्रोग्राम हैं जो वितरण के में परिवर्तित की जाती sample विधि।

   random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235
   

   Oryx अतिरिक्त रूप से TFP वितरण के बारे में जानकारी को JAX ट्रेस में एम्बेड करता है जो स्वचालित रूप से लॉग घनत्व की गणना करने में सक्षम बनाता है।

2. random_variable नाम के साथ कर सकते हैं टैग मूल्यों, उन्हें नीचे की ओर परिवर्तनों के लिए उपयोगी बनाने एक वैकल्पिक प्रदान करके name के लिए कीवर्ड तर्क random_variable । जब हम में एक सरणी पारित random_variable एक साथ name (जैसे random_variable(x, name='x') ), यह सिर्फ मूल्य और यह रिटर्न टैग करता है। अगर हम एक प्रतिदेय या TFP वितरण, में पारित random_variable रिटर्न एक प्रोग्राम है जो साथ इसके उत्पादन नमूना टैग name ।

जब निष्पादित ये टिप्पणियां कार्यक्रम के शब्दों को बदल नहीं है, लेकिन केवल जब तब्दील (यानी कार्यक्रम के साथ या के उपयोग के बिना समान परिणाम प्रदान करेंगे random_variable )।

आइए एक उदाहरण पर चलते हैं जहां हम कार्यक्षमता के दोनों टुकड़ों का एक साथ उपयोग करते हैं।

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

इस कार्यक्रम में हम मध्यवर्ती टैग किया है z और x , जो परिवर्तनों बनाता joint_sample , intervene , conditional और graph_replace नाम के बारे में पता 'z' और 'x' । हम ठीक से देखेंगे कि प्रत्येक परिवर्तन बाद में नामों का उपयोग कैसे करता है।

log_prob

log_prob समारोह परिवर्तन अपनी लॉग-घनत्व समारोह में एक ओरिक्स संभाव्य कार्यक्रम बदल देता है। यह लॉग-घनत्व फ़ंक्शन प्रोग्राम से इनपुट के रूप में एक संभावित नमूना लेता है और अंतर्निहित नमूना वितरण के तहत इसकी लॉग-घनत्व देता है।

log_prob :: Program -> (Sample -> LogDensity)

जैसा random_variable , यह प्रकार जहां TFP वितरण स्वचालित रूप से पंजीकृत हैं की एक रजिस्ट्री के माध्यम से काम करता है, इसलिए log_prob(tfd.Normal(0., 1.)) कॉल tfd.Normal(0., 1.).log_prob । अजगर कार्यों के लिए, तथापि, log_prob बयान नमूने के लिए JAX और दिखता का उपयोग कर कार्यक्रम निशान बनता है। log_prob परिवर्तन ज्यादातर कार्यक्रमों कि यादृच्छिक चर वापसी, प्रत्यक्ष या उलटी परिवर्तनों के माध्यम से नहीं बल्कि कार्यक्रमों पर कि नमूना मूल्यों आंतरिक कि वापस नहीं कर रहे हैं पर काम करता है। यह कार्यक्रम में आवश्यक कार्यों के उलटने नहीं कर सकते, log_prob एक त्रुटि फेंक देते हैं।

यहाँ के कुछ उदाहरण हैं log_prob विभिन्न कार्यक्रमों के लिए आवेदन किया।

1. log_prob प्रोग्राम हैं जो सीधे TFP वितरण (या अन्य पंजीकृत प्रकार) से नमूना और उनके मान पर काम करता है।

def normal(key):
  return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))

-0.9189385

1. log_prob (जैसे प्रोग्राम हैं जो द्विभाजित कार्यों का उपयोग कर यादृच्छिक variates बदलने से गणना करने के लिए नमूनों की लॉग-घनत्व में सक्षम है jnp.exp , jnp.tanh , jnp.split )।

def log_normal(key):
  return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))

-1.159165

आदेश से एक नमूना गणना करने के लिए में log_normal के लॉग-घनत्व, हम पहले उलटने की जरूरत exp , लेने log नमूने की, और उसके बाद का उपयोग कर प्रतिलोम लॉग-det Jacobian की मात्रा परिवर्तन सुधार जोड़ने exp (देखें परिवर्तन चर के विकिपीडिया से सूत्र)।

1. log_prob नमूनों की उत्पादन संरचनाओं की तरह है कि कार्यक्रमों के साथ काम करता है, अजगर शब्दकोशों या tuples।

def normal_2d(key):
  x = random_variable(
    tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
  x1, x2 = jnp.split(x, 2, 0)
  return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))

{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546

1. log_prob समारोह का पता लगाया गणना ग्राफ चलता है, दोनों आगे और उलटा मूल्यों की गणना (और उनके लॉग-det Jacobians) जब चर का एक अच्छी तरह से परिभाषित परिवर्तन के माध्यम से अपने आधार नमूना मूल्यों के साथ लौट आए मूल्यों कनेक्ट करने की कोशिश में आवश्यक। निम्नलिखित उदाहरण कार्यक्रम लें:

def complex_program(key):
  k1, k2 = random.split(key)
  z = random_variable(tfd.Normal(0., 1.))(k1)
  x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
  return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))

(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32))
-1.0967848

इस कार्यक्रम में, हम नमूना x सशर्त पर z , हम अर्थ का मूल्य की जरूरत है z इससे पहले कि हम में से लॉग-घनत्व की गणना कर सकता x । हालांकि, गणना करने के लिए z , हम पहले को उलटने के लिए है jnp.exp के लिए आवेदन किया z । इस प्रकार, आदेश के लॉग-घनत्व की गणना करने में x और z , log_prob पहले उत्पादन की विपरीत पहले करने के लिए की जरूरत है, और उसके बाद के माध्यम से इसे आगे पारित jax.nn.relu का मतलब गणना करने के लिए p(x | z) ।

के बारे में अधिक जानकारी के लिए log_prob , आप का उल्लेख कर सकते core.interpreters.log_prob । कार्यान्वयन में, log_prob बारीकी पर ही आधारित होता inverse JAX परिवर्तन; के बारे में अधिक जानने के लिए inverse , देख core.interpreters.inverse ।

joint_sample

अधिक जटिल और दिलचस्प प्रोग्रामों को परिभाषित करने के लिए, हम कुछ गुप्त रैंडम वैरिएबल का उपयोग करेंगे, यानी बिना देखे गए मानों वाले रैंडम वैरिएबल। के का उल्लेख करते latent_normal कार्यक्रम है कि नमूने एक यादृच्छिक मूल्य z कि का एक और यादृच्छिक मान मतलब के रूप में प्रयोग किया जाता है x ।

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

इस कार्यक्रम में, z अव्यक्त तो हम सिर्फ कॉल करने के लिए थे, तो है latent_normal(random.PRNGKey(0)) हम के वास्तविक मूल्य पता नहीं z कि पैदा करने के लिए जिम्मेदार है x ।

joint_sample एक परिवर्तन है कि एक अन्य कार्यक्रम में परिवर्तित हो एक प्रोग्राम है जो रिटर्न एक शब्दकोश मानचित्रण स्ट्रिंग नाम (टैग) उनके मूल्यों के लिए। काम करने के लिए, हमें यह सुनिश्चित करने की ज़रूरत है कि हम अव्यक्त चर को टैग करते हैं ताकि यह सुनिश्चित हो सके कि वे रूपांतरित फ़ंक्शन के आउटपुट में दिखाई दें।

joint_sample(latent_normal)(random.PRNGKey(0))

{'x': DeviceArray(0.01873656, dtype=float32),
 'z': DeviceArray(0.14389044, dtype=float32)}

ध्यान दें कि joint_sample रूपांतरण एक अन्य कार्यक्रम में एक प्रोग्राम है जो नमूने अपने अव्यक्त मूल्यों पर संयुक्त वितरण, ताकि हम आगे यह बदल सकता है। एमसीएमसी और VI जैसे एल्गोरिदम के लिए, अनुमान प्रक्रिया के हिस्से के रूप में संयुक्त वितरण की लॉग संभावना की गणना करना आम बात है। log_prob(latent_normal) नहीं काम है क्योंकि यह बाहर दरकिनार आवश्यकता करता है z , लेकिन हम उपयोग कर सकते हैं log_prob(joint_sample(latent_normal))

print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))

-50.03529
-5049.535

क्योंकि इस तरह के एक आम पैटर्न है, ओरिक्स भी एक है joint_log_prob परिवर्तन जो सिर्फ की रचना है log_prob और joint_sample ।

print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))

-50.03529
-5049.535

block

block परिवर्तन एक कार्यक्रम और नामों में से एक क्रम में लेता है और एक प्रोग्राम है जो हूबहू कि नीचे की ओर परिवर्तनों (जैसे को छोड़कर बर्ताव रिटर्न joint_sample ), बशर्ते नाम अनदेखी कर रहे हैं। जहां का एक उदाहरण block से उपयोगी है द्वारा "अवरुद्ध" मूल्यों संभावना में नमूना अव्यक्त चर पर एक पूर्व में एक संयुक्त वितरण परिवर्तित। उदाहरण के लिए, ले latent_normal , जो पहले एक ड्रॉ z ~ N(0, 1) फिर एक x | z ~ N(z, 1e-1) । block(latent_normal, names=['x']) एक प्रोग्राम है जो खाल है x नाम है, इसलिए यदि हम करते हैं joint_sample(block(latent_normal, names=['x'])) , हम बस के साथ एक शब्दकोश प्राप्त z उस में .

blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))

{'z': DeviceArray(0.14389044, dtype=float32)}

intervene

intervene बाहर से मूल्यों के साथ एक संभाव्य कार्यक्रम में परिवर्तन clobbers नमूने हैं। हमारे लिए वापस जा रहे latent_normal कार्यक्रम, मान लें कि हम एक ही कार्यक्रम चलाने में रुचि रखते थे लेकिन चाहते थे जाने z एक नया प्रोग्राम लिखने की तुलना में 4. बल्कि करने के लिए निर्धारित किया जा करने के लिए, हम उपयोग कर सकते हैं intervene के मान ओवरराइड करने के लिए z ।

intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();

/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

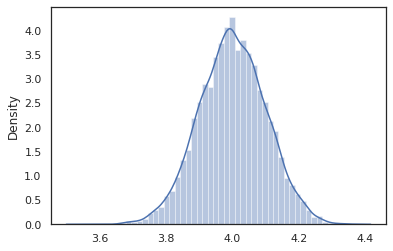
intervened से समारोह नमूने p(x | do(z = 4)) जो सिर्फ एक मानक सामान्य वितरण 4. पर केन्द्रित जब हम intervene एक विशेष मूल्य पर, कि मूल्य अब एक यादृच्छिक चर माना जाता है। इसका मतलब है कि z मूल्य जबकि टैग नहीं किया गया क्रियान्वित intervened ।

conditional

conditional रूपांतरण एक प्रोग्राम है जो नमूने में मूल्यों अव्यक्त है कि उन अव्यक्त मूल्यों पर स्थिति। हमारे पर वापस लौटते हुए latent_normal कार्यक्रम है, जो नमूने p(x) एक अव्यक्त साथ z , हम इसे एक सशर्त कार्यक्रम में बदल सकते हैं p(x | z) ।

cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()

99.87485
49.874847
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

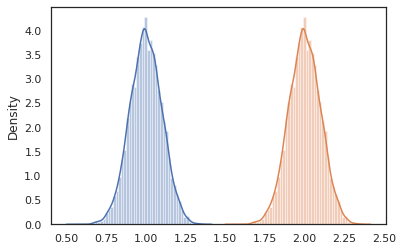
nest

जब हम अधिक जटिल प्रोग्राम बनाने के लिए संभाव्य प्रोग्राम बनाना शुरू करते हैं, तो कुछ महत्वपूर्ण तर्क वाले फ़ंक्शंस का पुन: उपयोग करना आम बात है। उदाहरण के लिए, अगर हम एक बायेसियन तंत्रिका नेटवर्क का निर्माण करना चाहते हैं, वहाँ एक महत्वपूर्ण हो सकता है dense प्रोग्राम है जो नमूने वजन और कार्यान्वित एक फॉरवर्ड पास।

हम कार्यों का पुन: उपयोग अगर, हालांकि, हम अंतिम कार्यक्रम है, जो की तरह परिवर्तनों द्वारा अस्वीकृत है में डुप्लिकेट टैग मूल्यों के साथ समाप्त हो सकता है joint_sample । हम उपयोग कर सकते हैं nest टैग बनाने के लिए "scopes" जहां एक नामित दायरे के अंदर किसी भी नमूने एक नेस्टेड शब्दकोश में सम्मिलित किया जाएगा।

def f(key):
  return random_variable(tfd.Normal(0., 1.), name='x')(key)

def g(key):
  k1, k2 = random.split(key)
  return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))

{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
 'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }

केस स्टडी: बायेसियन न्यूरल नेटवर्क

चलो क्लासिक वर्गीकृत करने के लिए एक बायेसियन तंत्रिका नेटवर्क प्रशिक्षण पर हमारे हाथ आजमाने फिशर आइरिस डाटासेट। यह अपेक्षाकृत छोटा और निम्न-आयामी है इसलिए हम सीधे एमसीएमसी के साथ पीछे के नमूने का प्रयास कर सकते हैं।

सबसे पहले, डेटासेट और कुछ अतिरिक्त उपयोगिताओं को Oryx से आयात करते हैं।

from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']

num_features = features.shape[-1]
num_classes = len(iris.target_names)

from oryx.experimental import mcmc
from oryx.util import summary, get_summaries

हम एक घनी परत को लागू करके शुरू करते हैं, जिसमें वज़न और पूर्वाग्रह पर सामान्य पुजारी होंगे। ऐसा करने के लिए, हम पहले एक परिभाषित dense उच्च आदेश समारोह है कि वांछित आउटपुट आयाम और सक्रियण समारोह में ले जाता है। dense समारोह एक संभाव्य प्रोग्राम है जो एक सशर्त वितरण का प्रतिनिधित्व करता है देता है p(h | x) जहां h एक घने परत के उत्पादन में है और x अपने इनपुट है। यह पहली बार नमूने वजन और पूर्वाग्रह और फिर उन्हें लागू होता है x ।

def dense(dim_out, activation=jax.nn.relu):
  def forward(key, x):
    dim_in = x.shape[-1]
    w_key, b_key = random.split(key)
    w = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
          name='w')(w_key)
    b = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
          name='b')(b_key)
    return activation(jnp.dot(w, x) + b)
  return forward

कई लिखने के लिए dense परतों को एक साथ, हम एक को लागू करेगा mlp (बहुपरत perceptron) उच्च आदेश समारोह जो और छिपा आकारों की सूची कक्षाओं की संख्या में ले जाता है। यह एक प्रोग्राम है जो बार-बार कॉल रिटर्न dense उचित उपयोग करते हुए hidden_size और अंत में अंतिम परत में प्रत्येक वर्ग के लिए logits देता है। नोट के उपयोग nest जो प्रत्येक परत के लिए नाम स्कोप पैदा करता है।

def mlp(hidden_sizes, num_classes):
  num_hidden = len(hidden_sizes)
  def forward(key, x):
    keys = random.split(key, num_hidden + 1)
    for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
      x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
    logits = nest(dense(num_classes, activation=lambda x: x),
                  scope=f'layer_{num_hidden + 1}')(keys[-1], x)
    return logits
  return forward

पूर्ण मॉडल को लागू करने के लिए, हमें लेबल को श्रेणीबद्ध यादृच्छिक चर के रूप में मॉडल करना होगा। हम एक को परिभाषित करेंगे predict समारोह जिनमें से एक डाटासेट में लेता xs (विशेषताएं) जो तब एक में पारित कर रहे हैं mlp का उपयोग कर vmap । जब हम का उपयोग vmap(partial(mlp, mlp_key)) , हम वेट का एक सेट का नमूना है, लेकिन सभी इनपुट से अधिक फॉरवर्ड पास नक्शा xs । इस का एक सेट का उत्पादन logits जो स्वतंत्र स्पष्ट वितरण parameterizes।

def predict(mlp):
  def forward(key, xs):
    mlp_key, label_key = random.split(key)
    logits = vmap(partial(mlp, mlp_key))(xs)
    return random_variable(
        tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
  return forward

वह पूरा मॉडल है! आइए एमसीएमसी का उपयोग बीएनएन वेट दिए गए डेटा के पीछे के नमूने के लिए करें; पहले हम प्रयोग कर एक BNN "टेम्पलेट" का निर्माण mlp ।

bnn = mlp([200, 200], num_classes)

हमारे मार्कोव श्रृंखला के लिए एक प्रारंभिक बिंदु का निर्माण करने के लिए हम उपयोग कर सकते हैं joint_sample एक डमी इनपुट के साथ।

weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())

dict_keys(['layer_1', 'layer_2', 'layer_3'])

संयुक्त वितरण लॉग संभाव्यता की गणना कई अनुमान एल्गोरिदम के लिए पर्याप्त है। चलो अब कहते हैं कि हम निरीक्षण करते हैं x और पीछे नमूने के लिए चाहते हैं p(z | x) । जटिल वितरण के लिए, हम बाहर हाशिए पर करने के लिए सक्षम नहीं होगा x (के लिए हालांकि latent_normal लेकिन हम कर सकते हैं) हम एक unnormalized लॉग घनत्व की गणना कर सकता log p(z, x) जहां x एक विशेष मूल्य के लिए तय हो गई है। हम पोस्टीरियर के नमूने के लिए एमसीएमसी के साथ असामान्य लॉग संभावना का उपयोग कर सकते हैं। आइए इस "पिन किए गए" लॉग प्रोब फ़ंक्शन को लिखें।

def target_log_prob(weights):
  return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)

अब हम उपयोग कर सकते हैं tfp.mcmc हमारे unnormalized लॉग घनत्व समारोह का उपयोग कर पीछे नमूने के लिए। ध्यान दें कि हम अपने नेस्टेड वजन का एक "चपटा" संस्करण का उपयोग करना होगा के साथ संगत होना करने के लिए शब्दकोश tfp.mcmc , तो हम JAX के पेड़ उपयोगिताओं का उपयोग समतल और unflatten करने के लिए।

@jit
def run_chain(key, weights):
  flat_state, sample_tree = jax.tree_flatten(weights)

  def flat_log_prob(*states):
    return target_log_prob(jax.tree_unflatten(sample_tree, states))

  def trace_fn(_, results):
    return results.inner_results.accepted_results.target_log_prob

  flat_states, log_probs = tfp.mcmc.sample_chain(
    1000,
    num_burnin_steps=9000,
    kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
        tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
        9000, target_accept_prob=0.7),
    trace_fn=trace_fn,
    current_state=flat_state,
    seed=key)
  samples = jax.tree_unflatten(sample_tree, flat_states)
  return samples, log_probs
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)

plt.plot(log_probs)
plt.show()

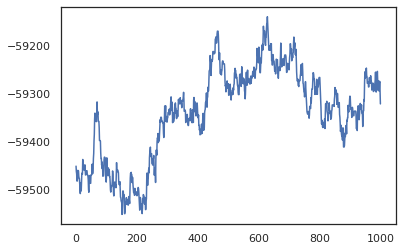
हम प्रशिक्षण सटीकता का बायेसियन मॉडल औसत (बीएमए) अनुमान लेने के लिए अपने नमूनों का उपयोग कर सकते हैं। यह गणना करने के लिए, हम उपयोग कर सकते हैं intervene के साथ bnn जो कि कुंजी से नमूने दिए जाते हैं के स्थान पर "सुई" पीछे वजन करने के लिए। प्रत्येक पीछे नमूने के लिए प्रत्येक डेटा बिंदु के लिए logits गणना के लिए, हम दोगुना कर सकते हैं vmap से अधिक posterior_weights और features ।

output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
    random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)

print('Average sample accuracy:', (
    output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
    output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())

Average sample accuracy: 0.9874067
BMA accuracy: 0.99333334

निष्कर्ष

ओरिक्स में, संभाव्य कार्यक्रम केवल जेएक्स फ़ंक्शन हैं जो इनपुट के रूप में (छद्म-) यादृच्छिकता लेते हैं। जेएक्स के फ़ंक्शन ट्रांसफॉर्मेशन सिस्टम के साथ ओरिक्स के कड़े एकीकरण के कारण, हम संभावित कार्यक्रमों को लिख और हेरफेर कर सकते हैं जैसे हम जेएक्स कोड लिख रहे हैं। यह जटिल मॉडल बनाने और अनुमान लगाने के लिए एक सरल लेकिन लचीली प्रणाली में परिणत होता है।