 הצג באתר TensorFlow.org הצג באתר TensorFlow.org |  הפעל בגוגל קולאב הפעל בגוגל קולאב |  צפה במקור ב-GitHub צפה במקור ב-GitHub |  הורד מחברת הורד מחברת |
pip install -q -U jax jaxlibpip install -q -Uq oryx -Ipip install -q tfp-nightly --upgrade
from functools import partial
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')
import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
import oryx
תכנות הסתברותי הוא הרעיון שאנו יכולים לבטא מודלים הסתברותיים באמצעות תכונות משפת תכנות. משימות כמו הסקה בייסיאנית או דחיקה לשוליים מסופקות לאחר מכן כתכונות שפה ויכולות להיות אוטומטיות.
Oryx מספקת מערכת תכנות הסתברותית שבה תוכניות הסתברותיות מתבטאות רק כפונקציות של Python; לאחר מכן, תוכניות אלו עוברות טרנספורמציה באמצעות טרנספורמציות פונקציות הניתנות לחיבור כמו אלה ב-JAX! הרעיון הוא להתחיל עם תוכניות פשוטות (כמו דגימה מנורמלי אקראי) ולחבר אותן יחד ליצירת מודלים (כמו רשת נוירונים בייסיאנית). נקודה חשוב של עיצוב PPL של הראם היא לאפשר תוכניות להיראות כמו פונקציות שאתה כבר לכתוב ושימוש ב JAX, אבל הם המבואר לעשות טרנספורמציות מודעות להם.
בואו לייבא תחילה את פונקציונליות הליבה של ה-PPL של Oryx.
from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest
מהן תוכניות הסתברותיות ב-Oryx?
ב-Oryx, תוכניות הסתברותיות הן רק פונקציות Python טהורות הפועלות על ערכי JAX ומפתחות פסאודו אקראיים ומחזירות מדגם אקראי. לפי התכנון, הם תואמים טרנספורמציות כמו jit ואת vmap . עם זאת, מערכת תכנות הסתברותית הראם מספקת כלים המאפשרים לך להוסיף הערות הפונקציות בדרכים מועילות.
בעקבות פילוסופית JAX של פונקציות טהורות, תכנית הסתברותית ראם היא פונקצית Python שלוקחת JAX PRNGKey כמו הטענה הראשונה שלה וכול מספר טיעוני מיזוג עקב. הפלט של הפונקציה נקרא "מדגם" ואותו הגבלות חלות jit -ed ו vmap פונקציות -ed חלות תוכניות הסתברותית (למשל אין בקרת זרימת נתונים תלוי, ללא תופעות לוואי, וכו '). זה שונה ממערכות תכנות הסתברותיות חיוניות רבות שבהן 'מדגם' הוא כל עקבות הביצוע, כולל ערכים פנימיים לביצוע התוכנית. נראה בהמשך איך ראם יכול לגשת ערכים פנימיים באמצעות joint_sample , נדון להלן.
Program :: PRNGKey -> ... -> Sample
הנה תוכנית "שלום עולם" כי דגימות מתוך התפלגות לוג-נורמלית .
def log_normal(key):
return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.) 0.8139614 /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
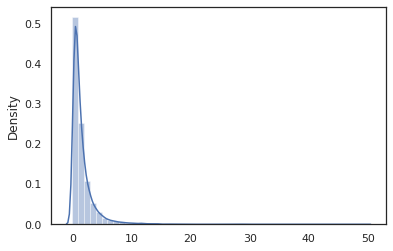
log_normal הפונקציה היא מעטפת דקה סביב הסתברות Tensorflow (פריון כולל) הפצה, אך במקום לקרוא tfd.Normal(0., 1.).sample , השתמשנו random_variable במקום. כפי שנראה בהמשך, random_variable מאפשרת לנו להמיר חפצים לתוך תוכניות הסתברותית, יחד עם פונקציונליות שימושיים נוספים.
אנו יכולים להמיר log_normal לתוך פונקציה יומן בצפיפות באמצעות log_prob טרנספורמציה:
print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()
-0.9189385
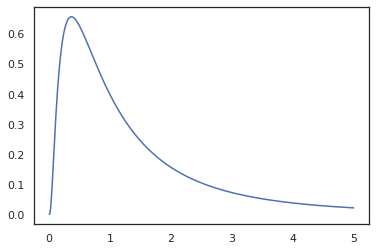
מכיוון שאנחנו כבר מבוארים הפונקציה עם random_variable , log_prob הוא מודע לכך שיש קריאת tfd.Normal(0., 1.).sample ומשתמש tfd.Normal(0., 1.).log_prob לחשב את חלוק הבסיס log prob. כדי להתמודד עם jnp.exp , ppl.log_prob מחשב צפיפויות אוטומטית באמצעות פונקציות bijective, מעקב אחר שינויים בנפח בחישוב שינוי-של-משתנה.
בשנת ראם, אנחנו יכולים לקחת תוכניות ולהפוך אותם באמצעות טרנספורמציות פונקציה - למשל, jax.jit או log_prob . עם זאת, Oryx לא יכולה לעשות זאת עם כל תוכנית; זה דורש פונקציות דגימה שרשמו את פונקציית צפיפות היומן שלהן עם Oryx. למרבה המזל, ראם רושמת אוטומטית הסתברות TensorFlow (הפריון הכולל) הפצות במערכת שלה.
כלי התכנות הסתברותי של Oryx
ל- Oryx יש מספר טרנספורמציות של פונקציות המיועדות לתכנות הסתברותי. נעבור על רובם ונביא כמה דוגמאות. בסופו של דבר, נחבר את הכל יחד למחקר מקרה של MCMC. ניתן גם לעיין בתיעוד עבור core.ppl.transformations לפרטים נוספים.
random_variable
random_variable יש שתי חתיכות ראשיות של פונקציונאלי, הן התמקדו מפרש פונקציות Python עם מידע שיכול לשמש טרנספורמציות.
random_variable'פועל כפונקצית הזהות כברירת מחדל, אך ניתן להשתמש רישומי סוג ספציפיים לאובייקטים להמיר programs.` הסתברותיתעבור סוגים callable (פונקציות Python, lambdas,
functools.partialים, וכו ') ו שרירותיobjectים (כמו JAXDeviceArrayים) זה רק יחזיר קלט שלה.random_variable(x: object) == x random_variable(f: Callable[...]) == fראם אוטומטית רושם הסתברות TensorFlow (פריון כולל) הפצות, אשר מומרות תוכניות הסתברותית שמקשרים של חלוק
sampleשיטה.random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235Oryx מטמיעה בנוסף מידע על הפצת ה-TFP לתוך עקבות JAX המאפשרת מחשוב אוטומטי של צפיפות יומן.
random_variableערכים יכול לתייג עם שמות, מה שהופך אותם שימושי עבור טרנספורמציות במורד הזרם, על ידי מתן פומביnameויכוח מילות מפתח כדיrandom_variable. כאשר אנו עוברים מערך לתוךrandom_variableיחד עםname(למשלrandom_variable(x, name='x')), זה רק מתייגת הערך וההחזר זה. אם אנחנו עוברים הפצת callable או פריון כולל,random_variableמחזיר תכנית תגים לדוגמא הפלט שלה עםname.
הערות אלו אינם משנים את הסמנטיקה של התוכנית כאשר להורג, אך רק כאשר משנים צורה (כלומר התוכנית תחזיר אותו ערך עם או ללא שימוש random_variable ).
בוא נעבור על דוגמה שבה אנו משתמשים בשני חלקי הפונקציונליות יחד.
def latent_normal(key):
z_key, x_key = random.split(key)
z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)
בתכנית זו אנו תייגנו את תשומות z ו- x , מה שהופך את תמורות joint_sample , intervene , conditional ו graph_replace מודע השמות 'z' ו 'x' . נעבור על איך בדיוק כל טרנספורמציה משתמשת בשמות מאוחר יותר.
log_prob
log_prob טרנספורמציה הפונקציה ממירה תוכנית הסתברותית ראם לתוך הפונקציה יומן בצפיפות שלה. פונקציה זו של צפיפות לוגין לוקחת דגימה פוטנציאלית מהתוכנית כקלט ומחזירה את צפיפות הלוג שלה תחת התפלגות הדגימה הבסיסית.
log_prob :: Program -> (Sample -> LogDensity)
כמו random_variable , זה עובד דרך רישום של סוגים שבו הפצות TFP רשום אוטומטית, כך log_prob(tfd.Normal(0., 1.)) קורא tfd.Normal(0., 1.).log_prob . עבור פונקציות Python, אולם, log_prob עקבות התוכנית באמצעות JAX ומחפש דגימה הצהרות. log_prob טרנספורמציה עובד על רוב התוכניות לחזור משתנים אקראי, ישירות או באמצעות טרנספורמציות להיפוך אבל לא על תוכניות ערכי מדגם פנימיים שלא מוחזרים. אם זה לא יכול להפוך את הפעולות הדרושות בתכנית, log_prob תזרוק שגיאה.
הנה כמה דוגמאות של log_prob להחיל תוכניות שונות.
-
log_probעובד על תוכניות ישירות מדגם מן הפצות הפריון הכולל (או סוגים אחרים רשום) ולהחזיר את הערכים שלהם.
def normal(key):
return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))
-0.9189385
-
log_probהוא מסוגל לחשב-צפיפויות יומן של דגימות מתוכניות שהופכים variates אקראי באמצעות פונקציות bijective (למשלjnp.exp,jnp.tanh,jnp.split).
def log_normal(key):
return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))
-1.159165
על מנת לחשב מדגם מן log_normal של יומן-צפיפות, אנחנו קודם צריכים להפוך את exp , לוקח את log של המדגם, ולאחר מכן להוסיף תיקון נפח-שינוי באמצעות יומן-Det הפוך יעקוביאן של exp (ראה שינוי של משתנה הנוסחה מוויקיפדיה).
-
log_probעבודות עם תוכניות מבנים הפלט של דגימות אוהבות, מילוני Python או tuples.
def normal_2d(key):
x = random_variable(
tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
x1, x2 = jnp.split(x, 2, 0)
return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))
{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546
-
log_probהולכת גרף החישוב לייחס של הפונקציה, מחשוב הוא ערכים קדימה הפוך (והיומן-Det שלהם Jacobians) בעת צורך בניסיון להתחבר לערכים חזרו עם ערכי שנדגמו לבסיסם באמצעות שינוי מוגדר היטב של משתנים. קח את התוכנית הבאה לדוגמה:
def complex_program(key):
k1, k2 = random.split(key)
z = random_variable(tfd.Normal(0., 1.))(k1)
x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))
(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32)) -1.0967848
בתוכנית זו, אנו מדגם x -תנאי על z , כלומר אנחנו צריכים את הערך של z לפני שניתן יהיה לחשב את צפיפות יומן של x . עם זאת, על מנת לחשב z , אנחנו קודם כל להפוך את jnp.exp להחיל z . לכן, על מנת לחשב את יומן-צפיפויות של x ו- z , log_prob צריך קודם להפוך את הפלט הראשון, ולאחר מכן תעביר את זה הלאה דרך jax.nn.relu לחשב את הממוצע של p(x | z) .
לקבלת מידע נוסף אודות log_prob , אתה יכול להתייחס core.interpreters.log_prob . בשנת היישום, log_prob הוא מבוסס על הנחה מקרוב של inverse טרנספורמציה JAX; כדי ללמוד עוד על inverse , לראות core.interpreters.inverse .
joint_sample
כדי להגדיר תוכניות מורכבות ומעניינות יותר, נשתמש בכמה משתנים אקראיים סמויים, כלומר משתנים אקראיים עם ערכים לא נצפים. בואו לעיין latent_normal תוכנית דגימות ערך אקראי z המשמש כממוצע של אחר ערך אקראי x .
def latent_normal(key):
z_key, x_key = random.split(key)
z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)
בתוכנית זו, z כך סמויה אם היינו פשוט להתקשר latent_normal(random.PRNGKey(0)) לא היינו יודעים את הערך האמיתי של z כי הוא אחראי ליצירת x .
joint_sample הוא טרנספורמציה שהופכת תוכנית לתוכנית אחרת שמחזירה שמות מחרוזת מילון הממפה (תגיות) לערכים שלהם. על מנת לעבוד, עלינו לוודא שאנו מתייגים את המשתנים הסמויים כדי להבטיח שהם יופיעו בפלט של הפונקציה שעברה טרנספורמציה.
joint_sample(latent_normal)(random.PRNGKey(0))
{'x': DeviceArray(0.01873656, dtype=float32),
'z': DeviceArray(0.14389044, dtype=float32)}
הערה כי joint_sample תמרות תוכנית לתוכנית אחרת כי דגימות חלוק המשותפת על הערכים הסמויים שלה, כדי שנוכל להפוך את זה עוד יותר. עבור אלגוריתמים כמו MCMC ו-VI, מקובל לחשב את ההסתברות ביומן של ההתפלגות המשותפת כחלק מהליך ההסקה. log_prob(latent_normal) לא עובד כי זה דורש לשוליים החוצה z , אבל אנחנו יכולים להשתמש log_prob(joint_sample(latent_normal)) .
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))
-50.03529 -5049.535
כיוון שמדובר בדפוס כזה נפוץ, ראם יש גם joint_log_prob הטרנספורמציה שהיא רק בהרכב של log_prob ו joint_sample .
print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))
-50.03529 -5049.535
block
block טרנספורמציה לוקח בתוכנית ואת רצף של שמות ומחזירה תוכנית שמתנהגת באופן זהה פרט לכך טרנספורמציות במורד הזרם (כמו joint_sample ), שמות סיפק מתעלמים. דוגמה שבה block הוא שימושי הוא המרת חלוקה משותפת לתוך מוקדם על המשתנים החבויים ידי "חסימה" הערכים שנדגמו ב הסבירות. לדוגמה, לקחת latent_normal , אשר הראשון מצייר z ~ N(0, 1) אז x | z ~ N(z, 1e-1) . block(latent_normal, names=['x']) היא תוכנית שמסתיר את x שם, אז אם אנחנו עושים joint_sample(block(latent_normal, names=['x'])) , נקבל מילון עם רק z בה .
blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))
{'z': DeviceArray(0.14389044, dtype=float32)}
intervene
intervene דגימות clobbers טרנספורמציה בתוכנית הסתברותית עם ערכים מבחוץ. נחזור שלנו latent_normal התוכנית, נניח שאנחנו מעוניינים לנהל אותה תוכנית אבל רצה z להיות קבוע 4. במקום לכתוב תוכנית חדשה, אנו יכולים להשתמש intervene כדי לעקוף את הערך של z .
intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
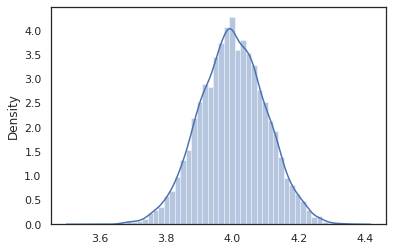
intervened דגימות פונקציה p(x | do(z = 4)) הנמצאת במרחק ההתפלגות הנורמלית הסטנדרטית מרוכז ב 4. כאשר אנו intervene על ערך מסוים, ערך זה אינו נחשב עוד משתנה אקראי. אמצעי זה כי z ערך לא יתויג תוך ביצוע intervened .
conditional
conditional תמרות תוכנית דגימות גלומות ערכים לתוך אחד כי תנאים על הערכים החבויים האלה. אם נחזור שלנו latent_normal התוכנית, אשר דגימות p(x) עם סמויה z , נוכל להמיר אותו לתוך התוכנית מותנה p(x | z) .
cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()
99.87485 49.874847 /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning) /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
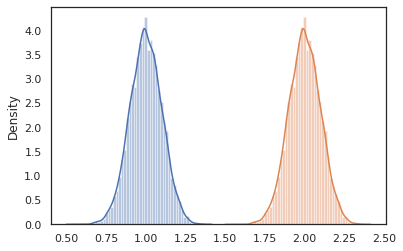
nest
כאשר אנו מתחילים לחבר תוכניות הסתברותיות כדי לבנות תוכניות מורכבות יותר, מקובל לעשות שימוש חוזר בפונקציות שיש להן היגיון חשוב. לדוגמה, אם אנחנו רוצים לבנות רשת עצבית בייס, ייתכן שיש חשיבות dense תוכנית משקולות דגימות וכן עוסקת בביצוע כדור לפנים.
אם אנחנו חוזרים פונקציות, לעומת זאת, אנו עלולים בסופו של דבר עם ערכים מתויגים כפול בתוכנית הגמר, זו חסום על ידי טרנספורמציות כמו joint_sample . אנו יכולים להשתמש nest כדי ליצור תג "סקופס" איפה כול דגימות בתוך בהיקף בשם תוכנסנה לתוך מילון מקונן.
def f(key):
return random_variable(tfd.Normal(0., 1.), name='x')(key)
def g(key):
k1, k2 = random.split(key)
return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))
{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }
מקרה מבחן: רשת נוירונים בייסיאנית
בואו לנסות את שלנו להכשיר רשת עצבית בייס לסיווג הקלאסי פישר איריס הנתונים. הוא קטן יחסית ובמימד נמוך כך שנוכל לנסות לדגום ישירות את החלק האחורי עם MCMC.
ראשית, בואו לייבא את מערך הנתונים וכמה כלי עזר נוספים מ-Oryx.
from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
from oryx.experimental import mcmc
from oryx.util import summary, get_summaries
אנו מתחילים ביישום שכבה צפופה, שתהיה לה קדימות רגילות על המשקולות וההטיה. כדי לעשות זאת, אנחנו קודם להגדיר dense פונקציה מסדר גבוהה שלוקחת בממד ותפקוד הפעלת תפוקה רצוי. dense הפונקציה מחזירה תוכנית הסתברותית מייצג פילוג מותנה p(h | x) שבו h הוא הפלט של שכבה צפופה x הוא הקלט שלה. זה דגימות ראשונות משקל ואת ההטיה ואז חלו עליהם x .
def dense(dim_out, activation=jax.nn.relu):
def forward(key, x):
dim_in = x.shape[-1]
w_key, b_key = random.split(key)
w = random_variable(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
name='w')(w_key)
b = random_variable(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
name='b')(b_key)
return activation(jnp.dot(w, x) + b)
return forward
כדי להלחין כמה dense שכבות יחד, נוכל ליישם mlp (רב שכבתי perceptron) פונקציה מסדר גבוהה שלוקח רשימת גדלים מוסתרים מספר כיתות. זה מחזיר תוכנית שוב ושוב קוראת dense באמצעות המתאים hidden_size ולבסוף מחזיר logits עבור כל כיתה בשכבה הסופי. שים לב לשימוש nest יוצרת היקפים שם עבור כול שכבה.
def mlp(hidden_sizes, num_classes):
num_hidden = len(hidden_sizes)
def forward(key, x):
keys = random.split(key, num_hidden + 1)
for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
logits = nest(dense(num_classes, activation=lambda x: x),
scope=f'layer_{num_hidden + 1}')(keys[-1], x)
return logits
return forward
כדי ליישם את המודל המלא, נצטרך לעצב את התוויות כמשתנים אקראיים קטגוריים. נצטרך להגדיר predict פונקציה אשר לוקח מערך נתונים של xs (תכונות) אשר מועברים לאחר מכן לתוך mlp באמצעות vmap . כאשר אנו משתמשים vmap(partial(mlp, mlp_key)) , אנו דוגמים סט יחיד של משקולות, אבל למפות את המסירה קדימה על כל קלט xs . זה מייצר מערכת של logits אשר parameterizes הפצות קטגורים עצמאיות.
def predict(mlp):
def forward(key, xs):
mlp_key, label_key = random.split(key)
logits = vmap(partial(mlp, mlp_key))(xs)
return random_variable(
tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
return forward
זה הדגם המלא! בואו נשתמש ב-MCMC כדי לדגום את החלק האחורי של משקלי ה-BNN שניתנו; הראשון אנו בונים BNN "תבנית" באמצעות mlp .
bnn = mlp([200, 200], num_classes)
כדי לבנות נקודת מוצא שרשרת מרקוב שלנו, אנחנו יכולים להשתמש joint_sample עם קלט דמה.
weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())
dict_keys(['layer_1', 'layer_2', 'layer_3'])
חישוב ההסתברות של יומן ההתפלגות המשותף מספיק עבור אלגוריתמים רבים של הסקת מסקנות. בואו עכשיו אומרים לנו להתבונן x ורוצים לטעום את האחוריים p(z | x) . עבור הפצות מורכבות, אנו לא נוכל לדחוק לשולים את x (אם כי עבור latent_normal שביכולתנו) אבל אנחנו יכולים לחשב צפיפות יומן unnormalized log p(z, x) שבו x הוא קבוע לערך מסוים. אנחנו יכולים להשתמש בהסתברות היומן הלא מנורמל עם MCMC כדי לדגום את האחורי. בוא נכתוב את פונקציית הניסוי ה"מוצמדת" הזו ביומן.
def target_log_prob(weights):
return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)
עכשיו אנחנו יכולים להשתמש tfp.mcmc לדגום את האחוריים באמצעות פונקציית צפיפות יומן unnormalized שלנו. הערה כי נצטרך להשתמש בגרסה "שטוח" של משקולות המקוננות שלנו המילון להיות תואם tfp.mcmc , כך אנו משתמשים Utilities העץ של JAX לשטח ו unflatten.
@jit
def run_chain(key, weights):
flat_state, sample_tree = jax.tree_flatten(weights)
def flat_log_prob(*states):
return target_log_prob(jax.tree_unflatten(sample_tree, states))
def trace_fn(_, results):
return results.inner_results.accepted_results.target_log_prob
flat_states, log_probs = tfp.mcmc.sample_chain(
1000,
num_burnin_steps=9000,
kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
9000, target_accept_prob=0.7),
trace_fn=trace_fn,
current_state=flat_state,
seed=key)
samples = jax.tree_unflatten(sample_tree, flat_states)
return samples, log_probs
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)
plt.plot(log_probs)
plt.show()
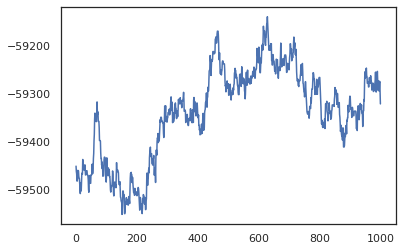
אנו יכולים להשתמש בדגימות שלנו כדי לקחת אומדן ממוצע של מודל בייסיאני (BMA) של דיוק האימון. כדי לחשב את זה, אנחנו יכולים להשתמש intervene עם bnn כדי "להזריק" אחורי משקולות במקום אלה נדגמים מהמפתח. כדי לחשב logits עבור כל נקודת נתונים עבור כל דגימה האחורי, נוכל להכפיל vmap מעל posterior_weights ואת features .
output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)
print('Average sample accuracy:', (
output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())
Average sample accuracy: 0.9874067 BMA accuracy: 0.99333334
סיכום
ב-Oryx, תוכניות הסתברותיות הן רק פונקציות JAX שמקבלות (פסאודו-) אקראיות כקלט. בגלל האינטגרציה ההדוקה של Oryx עם מערכת שינוי הפונקציות של JAX, אנחנו יכולים לכתוב ולתפעל תוכניות הסתברותיות כמו שאנחנו כותבים קוד JAX. כתוצאה מכך נוצרת מערכת פשוטה אך גמישה לבניית מודלים מורכבים ולביצוע מסקנות.
