 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
pip install -q -U jax jaxlibpip install -q -Uq oryx -Ipip install -q tfp-nightly --upgrade
from functools import partial
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')
import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
import oryx
La programmation probabiliste est l'idée que nous pouvons exprimer des modèles probabilistes en utilisant des fonctionnalités d'un langage de programmation. Des tâches telles que l'inférence bayésienne ou la marginalisation sont ensuite fournies en tant que fonctionnalités linguistiques et peuvent potentiellement être automatisées.
Oryx fournit un système de programmation probabiliste dans lequel les programmes probabilistes sont simplement exprimés sous forme de fonctions Python ; ces programmes sont ensuite transformés via des transformations de fonctions composables comme celles de JAX! L'idée est de commencer avec des programmes simples (comme l'échantillonnage à partir d'une normale aléatoire) et de les composer ensemble pour former des modèles (comme un réseau de neurones bayésien). Un point important de la conception PPL de Oryx est de permettre aux programmes de ressembler à des fonctions que vous souhaitez déjà écrire et à JAX, mais sont annotées de faire des transformations au courant.
Commençons par importer la fonctionnalité PPL de base d'Oryx.
from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest
Que sont les programmes probabilistes dans Oryx ?
Dans Oryx, les programmes probabilistes ne sont que de pures fonctions Python qui opèrent sur des valeurs JAX et des clés pseudo-aléatoires et renvoient un échantillon aléatoire. De par leur conception, ils sont compatibles avec les transformations comme jit et vmap . Cependant, le système de programmation probabiliste Oryx fournit des outils qui vous permettent d'annoter vos fonctions de manière utile.
Suite à la philosophie de JAX des fonctions pures, un programme probabiliste Oryx est une fonction qui prend un python JAX PRNGKey comme premier argument et un certain nombre d'arguments de conditionnement ultérieures. La sortie de la fonction est appelée un « échantillon » et les mêmes restrictions applicables aux jit -ed et vmap fonctions -ed s'appliquent aux programmes probabilistes (par exemple , pas de flux de contrôle dépendant des données, pas d' effets secondaires, etc.). Cela diffère de nombreux systèmes de programmation probabiliste impératifs dans lesquels un « échantillon » est la trace d'exécution entière, y compris les valeurs internes à l'exécution du programme. Nous verrons plus loin comment Oryx peut accéder à des valeurs internes à l' aide du joint_sample , discuté ci - dessous.
Program :: PRNGKey -> ... -> Sample
Voici un programme « Bonjour tout le monde » que les échantillons d'une distribution log-normale .
def log_normal(key):
return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.) 0.8139614 /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
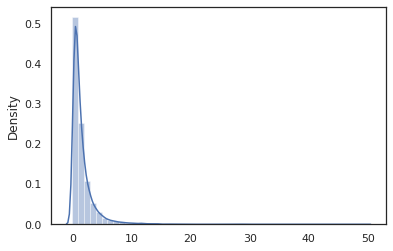
La log_normal fonction est une enveloppe mince autour d' une probabilité tensorflow (TFP) la distribution, mais au lieu d'appeler tfd.Normal(0., 1.).sample , nous avons utilisé random_variable à la place. Comme nous le verrons plus tard, random_variable nous permet de convertir des objets dans les programmes probabilistes, ainsi que d'autres fonctionnalités utiles.
Nous pouvons convertir log_normal en fonction de log-densité en utilisant la log_prob transformation:
print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()
-0.9189385
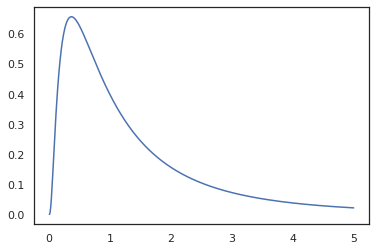
Parce que nous avons annotés la fonction avec random_variable , log_prob est au courant qu'il y avait un appel à tfd.Normal(0., 1.).sample et utilise tfd.Normal(0., 1.).log_prob pour calculer la distribution de base log prob. Pour gérer le jnp.exp , ppl.log_prob calcule automatiquement les densités par des fonctions bijectives, le suivi des changements de volume dans le calcul de changement de variable.
En Oryx, nous pouvons prendre des programmes et de les transformer en utilisant des transformations de fonction - par exemple, jax.jit ou log_prob . Oryx ne peut pas faire cela avec n'importe quel programme cependant ; il nécessite des fonctions d'échantillonnage qui ont enregistré leur fonction de densité logarithmique auprès d'Oryx. Heureusement, Oryx enregistre automatiquement tensorflow une probabilité distributions (TFP) dans le système.
Les outils de programmation probabiliste d'Oryx
Oryx a plusieurs transformations de fonctions orientées vers la programmation probabiliste. Nous allons passer en revue la plupart d'entre eux et fournir quelques exemples. À la fin, nous rassemblerons le tout dans une étude de cas MCMC. Vous pouvez également consulter la documentation core.ppl.transformations pour plus de détails.
random_variable
random_variable a deux principaux éléments de la fonctionnalité, à la fois l' accent sur annoter les fonctions Python avec des informations qui peuvent être utilisées dans les transformations.
random_variable'fonctionne comme la fonction d'identité par défaut, mais peut utiliser les enregistrements de spécifiques de type aux objets convertir en programs.` probabilistePour les types appelables (fonctions Python, lambdas,
functools.partials, etc.) et arbitraireobjectde (comme JAXDeviceArrays) elle retournera son entrée.random_variable(x: object) == x random_variable(f: Callable[...]) == fOryx enregistre automatiquement tensorflow Probabilité (PTF) distributions, qui sont convertis en des programmes probabilistes qui font appel de la distribution
sampleprocédé.random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235Oryx intègre en outre des informations sur la distribution TFP dans les traces JAX qui permettent de calculer automatiquement les densités de journaux.
random_variablevaleurs de balise peut avec des noms, ce qui les rend utiles pour les transformations en aval, en fournissant un optionnameargument mot - clé pourrandom_variable. Quand on passe un tableau enrandom_variableavec unname(par exemplerandom_variable(x, name='x')), il balises juste la valeur et le renvoie. Si nous passons dans une appelable ou la distribution TFP,random_variablerenvoie un programme que les balises de son échantillon de sortie avec lename.
Ces annotations ne changent pas la sémantique du programme lorsqu'il est exécuté, mais seulement lorsqu'il est transformé (le programme retourne la même valeur avec ou sans l'utilisation de random_variable ).
Passons en revue un exemple où nous utilisons les deux fonctionnalités ensemble.
def latent_normal(key):
z_key, x_key = random.split(key)
z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)
Dans ce programme , nous avons étiqueté les intermédiaires z et x , ce qui rend les transformations joint_sample , intervene , sous conditional et graph_replace au courant des noms 'z' et 'x' . Nous verrons plus tard exactement comment chaque transformation utilise les noms.
log_prob
La log_prob transformation convertit un programme probabiliste Oryx dans sa fonction log-densité. Cette fonction de densité logarithmique prend un échantillon potentiel du programme en entrée et renvoie sa densité logarithmique sous la distribution d'échantillonnage sous-jacente.
log_prob :: Program -> (Sample -> LogDensity)
Comme random_variable , cela fonctionne par l' intermédiaire d' un registre des types où les distributions TFP sont automatiquement enregistrées, si log_prob(tfd.Normal(0., 1.)) appelle tfd.Normal(0., 1.).log_prob . Pour les fonctions Python, cependant, log_prob le même programme en utilisant JAX et cherche des déclarations d' échantillonnage. La log_prob transformation fonctionne sur la plupart des programmes qui renvoient des variables aléatoires, directement ou via des transformations inversible mais pas sur les programmes que les valeurs d'échantillonnage interne qui ne sont pas retournés. Si elle ne peut pas inverser les opérations nécessaires dans le programme, log_prob lancera une erreur.
Voici quelques exemples de log_prob appliqués à divers programmes.
-
log_probtravaille sur les programmes que l' échantillon directement à partir de distributions TFP (ou d' autres types enregistrés) , et le rendement de leurs valeurs.
def normal(key):
return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))
-0.9189385
-
log_probest en mesure de calculer log-densités d'échantillons de programmes qui transforment des nombres aléatoires en utilisant des fonctions bijectives (par exemplejnp.exp,jnp.tanh,jnp.split).
def log_normal(key):
return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))
-1.159165
Afin de calculer un échantillon de log_normal log densité de, nous avons d' abord besoin d'inverser l' exp , en prenant le log de l'échantillon, puis ajoutez une correction changement de volume à l' aide du log-det inverse jacobienne exp (voir le changement de la variable formule de Wikipedia).
-
log_probtravaille avec les programmes que les structures de production d'échantillons aiment, dictionnaires Python ou tuples.
def normal_2d(key):
x = random_variable(
tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
x1, x2 = jnp.split(x, 2, 0)
return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))
{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546
-
log_probparcourt le graphe de calcul tracé de la fonction, le calcul de deux valeurs vers l' avant et inverse (et leur log-det jacobiennes) lorsque cela est nécessaire dans le but de connecter les valeurs renvoyées avec les valeurs échantillonnées de base par l' intermédiaire d' un changement bien défini de variables. Prenons l'exemple de programme suivant :
def complex_program(key):
k1, k2 = random.split(key)
z = random_variable(tfd.Normal(0., 1.))(k1)
x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))
(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32)) -1.0967848
Dans ce programme, on échantillonne x conditionnellement z , ce qui signifie nous avons besoin de la valeur de z avant de pouvoir calculer le log densité de x . Cependant, pour calculer z , il faut d' abord inverser la jnp.exp appliquée à z . Ainsi, pour calculer les densités de log- x et z , log_prob doit d'abord inverser la première sortie, et passer ensuite en avant par le jax.nn.relu pour calculer la moyenne de p(x | z) .
Pour plus d' informations sur log_prob , vous pouvez vous référer à core.interpreters.log_prob . Dans la mise en œuvre, log_prob est étroitement basée hors de l' inverse de transformation de JAX; pour en savoir plus sur inverse , voir core.interpreters.inverse .
joint_sample
Pour définir des programmes plus complexes et intéressants, nous utiliserons des variables aléatoires latentes, c'est-à-dire des variables aléatoires avec des valeurs non observées. Allons font référence au latent_normal programme que les échantillons d' une valeur aléatoire z qui est utilisée comme la moyenne d' une autre valeur aléatoire x .
def latent_normal(key):
z_key, x_key = random.split(key)
z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)
Dans ce programme, z est donc latent si nous devions simplement appeler latent_normal(random.PRNGKey(0)) nous ne saurions pas la valeur réelle de z qui est responsable de la génération x .
joint_sample est une transformation qui transforme un programme dans un autre programme qui renvoie un nom de chaîne de cartographie dictionnaire (tags) à leurs valeurs. Pour fonctionner, nous devons nous assurer de baliser les variables latentes pour nous assurer qu'elles apparaissent dans la sortie de la fonction transformée.
joint_sample(latent_normal)(random.PRNGKey(0))
{'x': DeviceArray(0.01873656, dtype=float32),
'z': DeviceArray(0.14389044, dtype=float32)}
Notez que joint_sample transforme un programme dans un autre programme que les échantillons de la distribution conjointe sur ses valeurs latentes, afin que nous puissions encore le transformer. Pour les algorithmes tels que MCMC et VI, il est courant de calculer la probabilité de log de la distribution conjointe dans le cadre de la procédure d'inférence. log_prob(latent_normal) ne fonctionne pas , car il faut marginaliser sur z , mais nous pouvons utiliser log_prob(joint_sample(latent_normal)) .
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))
-50.03529 -5049.535
Parce que c'est un schéma commun, Oryx a aussi une joint_log_prob transformation qui est juste la composition de log_prob et joint_sample .
print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))
-50.03529 -5049.535
block
Le block de transformation prend dans un programme et une séquence de noms et renvoie un programme qui se comporte de manière identique à l' exception que dans les transformations en aval (comme joint_sample ), les noms fournis sont ignorés. Un exemple de cas où le block est à portée de main est de convertir une distribution conjointe en avant sur les variables latentes par « blocage » les valeurs échantillonnées de la probabilité. Par exemple, prendre latent_normal , qui dessine d' abord un z ~ N(0, 1) puis un x | z ~ N(z, 1e-1) . block(latent_normal, names=['x']) est un programme qui cache le x nom, donc si nous faisons joint_sample(block(latent_normal, names=['x'])) , on obtient un dictionnaire avec juste z dans ce .
blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))
{'z': DeviceArray(0.14389044, dtype=float32)}
intervene
Le intervene des échantillons de aplatit de transformation dans un programme probabiliste avec des valeurs de l'extérieur. Pour en revenir à notre latent_normal programme, nous allons dire que nous étions intéressés à avoir le même programme mais je voulais z à être fixé à 4. Plutôt que d' écrire un nouveau programme, nous pouvons utiliser intervene pour remplacer la valeur de z .
intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
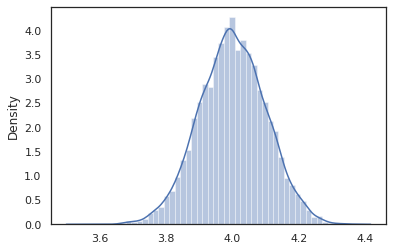
Les intervened des échantillons de fonction de p(x | do(z = 4)) qui est juste une distribution normale centrée à 4. Lorsque nous intervene sur une valeur particulière, cette valeur n'est plus considérée comme une variable aléatoire. Cela signifie qu'une z valeur ne sera pas taggés lors de l' exécution intervened .
conditional
conditional transforme un programme que les échantillons des valeurs latentes dans l' une que les conditions sur ces valeurs latentes. De retour à notre latent_normal programme, des échantillons p(x) avec une latente z , on peut le convertir en un programme conditionnel p(x | z) .
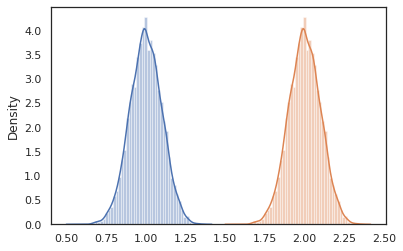
cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()
99.87485 49.874847 /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning) /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
nest
Lorsque nous commençons à composer des programmes probabilistes pour en construire des plus complexes, il est courant de réutiliser des fonctions qui ont une logique importante. Par exemple, si nous aimerions construire un réseau de neurones bayésien, il pourrait y avoir un important dense programme que les poids des échantillons et exécute une passe en avant.
Si nous réutilisons les fonctions, cependant, nous pourrions finir avec les valeurs marquées en double dans le programme final, qui est rejeté par des transformations comme joint_sample . Nous pouvons utiliser le nest pour créer la balise « Scopes » où tous les échantillons à l' intérieur d'un champ nommé sera inséré dans un dictionnaire imbriqué.
def f(key):
return random_variable(tfd.Normal(0., 1.), name='x')(key)
def g(key):
k1, k2 = random.split(key)
return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))
{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }
Étude de cas : réseau de neurones bayésien
Essayons notre main à la formation d' un réseau de neurones bayésien pour classer le classique Fisher Iris ensemble de données. Il est relativement petit et de faible dimension, nous pouvons donc essayer d'échantillonner directement le postérieur avec MCMC.
Tout d'abord, importons l'ensemble de données et quelques utilitaires supplémentaires depuis Oryx.
from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
from oryx.experimental import mcmc
from oryx.util import summary, get_summaries
Nous commençons par implémenter une couche dense, qui aura des priors normaux sur les poids et le biais. Pour ce faire, nous définissons d' abord une dense fonction d'ordre supérieur qui prend la dimension de sortie souhaitée et la fonction activation. La dense fonction retourne un programme probabiliste qui représente une distribution conditionnelle p(h | x) où h est la sortie d'une couche dense et x est son entrée. Il échantillonne le premier poids et les préjugés et les applique à x .
def dense(dim_out, activation=jax.nn.relu):
def forward(key, x):
dim_in = x.shape[-1]
w_key, b_key = random.split(key)
w = random_variable(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
name='w')(w_key)
b = random_variable(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
name='b')(b_key)
return activation(jnp.dot(w, x) + b)
return forward
Pour composer plusieurs dense couches ensemble, nous mettrons en œuvre un mlp (perceptron multicouche) fonction d'ordre supérieur qui prend dans une liste de tailles cachées et un certain nombre de classes. Il retourne un programme qui appelle à plusieurs reprises dense en utilisant le approprié hidden_size et enfin retourne logits pour chaque classe dans la couche finale. Notez l'utilisation du nest qui crée des étendues de nom pour chaque couche.
def mlp(hidden_sizes, num_classes):
num_hidden = len(hidden_sizes)
def forward(key, x):
keys = random.split(key, num_hidden + 1)
for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
logits = nest(dense(num_classes, activation=lambda x: x),
scope=f'layer_{num_hidden + 1}')(keys[-1], x)
return logits
return forward
Pour implémenter le modèle complet, nous devrons modéliser les étiquettes en tant que variables aléatoires catégorielles. Nous allons définir une predict fonction qui prend dans un ensemble de données xs (les caractéristiques) qui sont ensuite passés dans un mlp en utilisant vmap . Lorsque nous utilisons vmap(partial(mlp, mlp_key)) , on échantillonne un seul ensemble de poids, mais cartographier la passe en avant sur toutes les entrées xs . Cela produit un ensemble de logits qui paramétrise distributions catégoriques indépendantes.
def predict(mlp):
def forward(key, xs):
mlp_key, label_key = random.split(key)
logits = vmap(partial(mlp, mlp_key))(xs)
return random_variable(
tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
return forward
C'est le modèle complet ! Utilisons MCMC pour échantillonner le postérieur des poids BNN donnés ; D' abord , nous construisons un BNN « modèle » en utilisant mlp .
bnn = mlp([200, 200], num_classes)
Pour construire un point de départ pour notre chaîne de Markov, nous pouvons utiliser joint_sample avec une entrée factice.
weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())
dict_keys(['layer_1', 'layer_2', 'layer_3'])
Le calcul de la probabilité de log de distribution conjointe est suffisant pour de nombreux algorithmes d'inférence. Disons que maintenant , nous observons x et que vous voulez échantillonner la partie postérieure p(z | x) . Pour les distributions complexes, nous ne serons pas en mesure de marginaliser des x (bien que pour latent_normal nous pouvons) mais nous pouvons calculer une densité de log non normalisée log p(z, x) où x est fixé à une valeur particulière. Nous pouvons utiliser la probabilité log non normalisée avec MCMC pour échantillonner la postérieure. Écrivons cette fonction de prob de journal " épinglée ".
def target_log_prob(weights):
return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)
Maintenant , nous pouvons utiliser tfp.mcmc pour échantillonner la partie postérieure en utilisant notre fonction de densité non normalisée du journal. Notez que nous devons utiliser une version « aplati » de nos poids imbriqués dictionnaire pour être compatibles avec tfp.mcmc , nous utilisons donc les services publics d'arbres de Jax pour aplatir et Redresser.
@jit
def run_chain(key, weights):
flat_state, sample_tree = jax.tree_flatten(weights)
def flat_log_prob(*states):
return target_log_prob(jax.tree_unflatten(sample_tree, states))
def trace_fn(_, results):
return results.inner_results.accepted_results.target_log_prob
flat_states, log_probs = tfp.mcmc.sample_chain(
1000,
num_burnin_steps=9000,
kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
9000, target_accept_prob=0.7),
trace_fn=trace_fn,
current_state=flat_state,
seed=key)
samples = jax.tree_unflatten(sample_tree, flat_states)
return samples, log_probs
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)
plt.plot(log_probs)
plt.show()
Nous pouvons utiliser nos échantillons pour obtenir une estimation de la moyenne du modèle bayésien (BMA) de la précision de l'apprentissage. Pour le calculer, nous pouvons utiliser intervene avec bnn pour « inject » postérieur poids à la place de ceux qui sont isolées à partir du clavier. Pour calculer logits pour chaque point de données pour chaque échantillon postérieur, on peut doubler vmap sur posterior_weights et features .
output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)
print('Average sample accuracy:', (
output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())
Average sample accuracy: 0.9874067 BMA accuracy: 0.99333334
Conclusion
Dans Oryx, les programmes probabilistes ne sont que des fonctions JAX qui prennent en entrée le (pseudo-)aléatoire. En raison de l'étroite intégration d'Oryx avec le système de transformation de fonctions de JAX, nous pouvons écrire et manipuler des programmes probabilistes comme nous écrivons du code JAX. Il en résulte un système simple mais flexible pour construire des modèles complexes et faire des inférences.
