ওরিক্সে সম্ভাব্য প্রোগ্রামিং

TensorFlow.org এ দেখুন

Google Colab-এ চালান

GitHub-এ উৎস দেখুন

নোটবুক ডাউনলোড করুন

pip install -q -U jax jaxlib
pip install -q -Uq oryx -I
pip install -q tfp-nightly --upgrade

from functools import partial

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')

import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random

from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions

import oryx

প্রোব্যাবিলিস্টিক প্রোগ্রামিং হল এমন ধারণা যা আমরা প্রোগ্রামিং ভাষার বৈশিষ্ট্যগুলি ব্যবহার করে সম্ভাব্য মডেলগুলি প্রকাশ করতে পারি। বায়েসিয়ান ইনফারেন্স বা প্রান্তিককরণের মতো কাজগুলি তারপর ভাষা বৈশিষ্ট্য হিসাবে প্রদান করা হয় এবং সম্ভাব্য স্বয়ংক্রিয় হতে পারে।

ওরিক্স একটি সম্ভাব্য প্রোগ্রামিং সিস্টেম সরবরাহ করে যেখানে সম্ভাব্য প্রোগ্রামগুলিকে পাইথন ফাংশন হিসাবে প্রকাশ করা হয়; এই প্রোগ্রামগুলি তারপর JAX-এর মতো কম্পোজেবল ফাংশন ট্রান্সফর্মেশনের মাধ্যমে রূপান্তরিত হয়! ধারণাটি হ'ল সাধারণ প্রোগ্রামগুলি দিয়ে শুরু করা (যেমন একটি এলোমেলো সাধারণ থেকে নমুনা নেওয়া) এবং মডেলগুলি তৈরি করার জন্য তাদের একসাথে রচনা করা (যেমন একটি বায়েসিয়ান নিউরাল নেটওয়ার্ক)। আফ্রিকার একজাতীয় কৃষ্ণসার মৃগ এর PPL নকশা একটি গুরুত্বপূর্ণ পয়েন্ট ফাংশন আপনি ইতিমধ্যে লিখতে চাই এবং Jax ব্যবহারের মত দেখুন প্রোগ্রাম সক্রিয় করতে, কিন্তু রূপান্তরের তাদের সম্পর্কে অবগত করতে সটীক করছে।

আসুন প্রথমে ওরিক্সের মূল PPL কার্যকারিতা আমদানি করি।

from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest

ওরিক্সে সম্ভাব্য প্রোগ্রামগুলি কী কী?

ওরিক্স-এ, সম্ভাব্য প্রোগ্রামগুলি কেবলমাত্র বিশুদ্ধ পাইথন ফাংশন যা JAX মান এবং সিউডোর্যান্ডম কীগুলিতে কাজ করে এবং একটি এলোমেলো নমুনা প্রদান করে। নকশা, তারা মত রূপান্তরের সঙ্গে সামঞ্জস্যপূর্ণ jit এবং vmap । যাইহোক, আফ্রিকার একজাতীয় কৃষ্ণসার মৃগ সম্ভাব্য প্রোগ্রামিং সিস্টেম টুলস যে আপনার দরকারী উপায়ে আপনার ফাংশন টীকা করতে সক্ষম প্রদান করে।

বিশুদ্ধ ফাংশন Jax দর্শন অনুসরণ করে একটি আফ্রিকার একজাতীয় কৃষ্ণসার মৃগ সম্ভাব্য প্রোগ্রামটি পাইথন ফাংশন যা A Jax লাগে PRNGKey তার প্রথম যুক্তি এবং পরবর্তী কন্ডিশনার আর্গুমেন্ট যে কোন সংখ্যার হিসাবে। ফাংশনের আউটপুট একটি "নমুনা" এবং একই সীমাবদ্ধতা প্রযোজ্য বলা হয় jit -ed এবং vmap -ed ফাংশন সম্ভাব্য প্রোগ্রাম (যেমন কোন তথ্য নির্ভর নিয়ন্ত্রণ প্রবাহ, কোন পার্শ্ব প্রতিক্রিয়া, ইত্যাদি) প্রয়োগ করা হয়। এটি অনেক আবশ্যিক সম্ভাব্য প্রোগ্রামিং সিস্টেমের থেকে আলাদা যেখানে একটি 'নমুনা' হল সম্পূর্ণ এক্সিকিউশন ট্রেস, যার মধ্যে প্রোগ্রামের এক্সিকিউশনের অভ্যন্তরীণ মানগুলিও রয়েছে। আমরা পরে দেখতে হবে কিভাবে আফ্রিকার একজাতীয় কৃষ্ণসার মৃগ ব্যবহার অভ্যন্তরীণ মান অ্যাক্সেস করতে পারেন joint_sample , নীচের আলোচনা করেছেন।

Program :: PRNGKey -> ... -> Sample

এখানে একটি "ওহে দুনিয়া" প্রোগ্রাম করে একটি থেকে নমুনা লগ-স্বাভাবিক বন্টন ।

def log_normal(key):
  return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))

print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
0.8139614
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

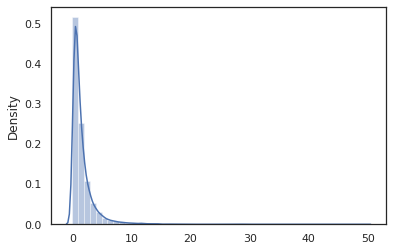
log_normal ফাংশন একটি কাছাকাছি একটি পাতলা মোড়কের হয় Tensorflow সম্ভাব্যতা (TFP) বন্টন, কিন্তু এর পরিবর্তে কলিং tfd.Normal(0., 1.).sample , আমরা ব্যবহার করেছি random_variable পরিবর্তে। আমরা পরে দেখতে পাবেন যে, random_variable সম্ভাব্য প্রোগ্রাম মধ্যে বস্তু রূপান্তর করতে, অন্যান্য দরকারী বৈশিষ্ট্য সহ বরাবর সক্ষম করে।

আমরা রূপান্তর করতে পারেন log_normal ব্যবহার করে একটি লগ-ঘনত্ব ফাংশন মধ্যে log_prob রূপান্তর:

print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()

-0.9189385

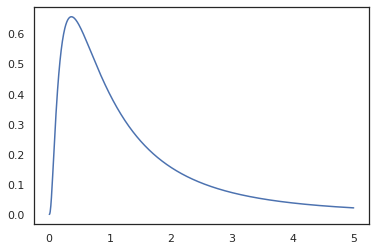
যেহেতু আমরা সঙ্গে ফাংশন সটীক থাকেন random_variable , log_prob একটি কল ছিল সচেতন tfd.Normal(0., 1.).sample ও ব্যবহার করে tfd.Normal(0., 1.).log_prob বেস বন্টন গনা লগ সমস্যা হ্যান্ডেল করতে jnp.exp , ppl.log_prob স্বয়ংক্রিয়ভাবে ঘনত্বের bijective ফাংশন মাধ্যমে, নির্ণয় পরিবর্তন অফ পরিবর্তনশীল গণনার ভলিউম পরিবর্তন সম্পর্কে অবগত থাকার।

আফ্রিকার একজাতীয় কৃষ্ণসার মৃগ, আমরা প্রোগ্রাম গ্রহণ করা এবং ফাংশন রূপান্তরের ব্যবহার করে সেগুলি রুপান্তর করতে পারেন - উদাহরণস্বরূপ, জন্য jax.jit বা log_prob । Oryx যদিও কোনো প্রোগ্রাম দিয়ে এটা করতে পারে না; এটির জন্য স্যাম্পলিং ফাংশন প্রয়োজন যেগুলি ওরিক্সের সাথে তাদের লগ ঘনত্বের ফাংশন নিবন্ধিত করেছে। সৌভাগ্যবসত, আফ্রিকার একজাতীয় কৃষ্ণসার মৃগ স্বয়ংক্রিয়ভাবে খাতাপত্র TensorFlow সম্ভাব্যতা তার সিস্টেমের মধ্যে (TFP) ডিস্ট্রিবিউশন।

ওরিক্সের সম্ভাব্য প্রোগ্রামিং টুল

ওরিক্সের বেশ কিছু ফাংশন ট্রান্সফর্মেশন আছে যা সম্ভাব্য প্রোগ্রামিং এর দিকে লক্ষ্য করা যায়। আমরা তাদের বেশিরভাগের উপর যেতে এবং কিছু উদাহরণ প্রদান করব। শেষ পর্যন্ত, আমরা এটিকে একটি MCMC কেস স্টাডিতে একসাথে রাখব। এছাড়াও আপনি ডকুমেন্টেশন পাঠাতে পারেন core.ppl.transformations আরো বিস্তারিত জানার জন্য।

random_variable

random_variable কার্যকারিতা দুটি প্রধান টুকরা আছে, উভয় তথ্য রূপান্তরের ব্যবহার করা যেতে পারে সঙ্গে পাইথন ফাংশন টিকা উপর দৃষ্টি নিবদ্ধ করা।

1. random_variable 'ডিফল্ট ভাবে পরিচয় ফাংশন হিসাবে কাজ করে, কিন্তু সম্ভাব্য programs.` রূপান্তর বস্তু টাইপ-নির্দিষ্ট নিবন্ধীকরণের ব্যবহার করতে পারেন

   Callable প্রকার (পাইথন ফাংশন, lambdas জন্য functools.partial গুলি, ইত্যাদি) এবং নির্বিচারে object গুলি (মত Jax DeviceArray গুলি) এটা ঠিক এর ইনপুট ফিরে আসবে।

   random_variable(x: object) == x
   random_variable(f: Callable[...]) == f
   

   আফ্রিকার একজাতীয় কৃষ্ণসার মৃগ স্বয়ংক্রিয়ভাবে খাতাপত্র TensorFlow সম্ভাব্যতা (TFP) ডিস্ট্রিবিউশন, যা সম্ভাব্য প্রোগ্রাম ডিস্ট্রিবিউশনের কল রূপান্তরিত হয় sample পদ্ধতি।

   random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235
   

   অরিক্স অতিরিক্তভাবে JAX ট্রেসে TFP বিতরণ সম্পর্কে তথ্য এম্বেড করে যা স্বয়ংক্রিয়ভাবে লগ ঘনত্ব গণনা করতে সক্ষম করে।

2. random_variable নামের সাথে করতে পারেন ট্যাগ মূল্যবোধ, তাদের স্রোতবরাবর রূপান্তরের জন্য দরকারী উপার্জন একটি ঐচ্ছিক প্রদানের মাধ্যমে name থেকে শব্দ যুক্তি random_variable । আমরা যখন একটি বিন্যাস পাস random_variable একটি সহ name (যেমন random_variable(x, name='x') ), এটা ঠিক মান এবং এটি আয় ট্যাগ। আমরা যদি callable বা TFP বন্টন, মধ্যে পাস random_variable আয় একটি প্রোগ্রাম যা সঙ্গে তার আউটপুট নমুনা ট্যাগ name ।

যখন মৃত্যুদন্ড কার্যকর এই টীকা প্রোগ্রামের শব্দার্থবিদ্যা পরিবর্তন করবেন না, কিন্তু শুধুমাত্র যখন রুপান্তরিত (অর্থাত প্রোগ্রামের সাথে বা ব্যবহার না করে একই মান ফিরে আসবে random_variable )।

আসুন একটি উদাহরণে যাই যেখানে আমরা কার্যকারিতার উভয় অংশ একসাথে ব্যবহার করি।

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

এই প্রোগ্রাম আমরা intermediates বাঁধা থাকেন z এবং x , যা রূপান্তরের তোলে joint_sample , intervene , conditional এবং graph_replace নামের সচেতন 'z' এবং 'x' । আমরা ঠিক কিভাবে প্রতিটি রূপান্তর পরে নাম ব্যবহার করে তা দেখতে হবে.

log_prob

log_prob ফাংশন রূপান্তর তার লগ-ঘনত্ব ফাংশন মধ্যে একটি আফ্রিকার একজাতীয় কৃষ্ণসার মৃগ সম্ভাব্য কর্মসূচি পরিবর্তন করে। এই লগ-ঘনত্ব ফাংশন ইনপুট হিসাবে প্রোগ্রাম থেকে একটি সম্ভাব্য নমুনা নেয় এবং অন্তর্নিহিত নমুনা বিতরণের অধীনে এর লগ-ঘনত্ব প্রদান করে।

log_prob :: Program -> (Sample -> LogDensity)

ভালো লেগেছে random_variable , এটা ধরনের যেখানে TFP ডিস্ট্রিবিউশন স্বয়ংক্রিয়ভাবে নিবন্ধিত একটি রেজিস্ট্রি মাধ্যমে কাজ করে, তাই log_prob(tfd.Normal(0., 1.)) কল tfd.Normal(0., 1.).log_prob । পাইথন কাজগুলির জন্য অবশ্য log_prob বিবৃতি স্যাম্পলিং জন্য Jax এবং সৌন্দর্য ব্যবহার প্রোগ্রাম ট্রেস। log_prob রূপান্তর সবচেয়ে প্রোগ্রাম যা র্যান্ডম ভেরিয়েবল ফিরে সরাসরি বা বিপরীত রূপান্তরের মাধ্যমে কিন্তু প্রোগ্রাম যে নমুনা মান অভ্যন্তরীণভাবে যে ফিরে নেই কাজ করে। এটা প্রোগ্রামে প্রয়োজনীয় অপারেশন invert করতে না পারেন, log_prob একটি ত্রুটি নিক্ষেপ করা হবে।

এখানে কিছু উদাহরণ log_prob বিভিন্ন কর্মসূচি প্রয়োগ করা হয়েছিল।

1. log_prob প্রোগ্রাম সরাসরি TFP ডিস্ট্রিবিউশন (অথবা অন্যান্য নিবন্ধিত ধরনের) থেকে নমুনা এবং তাদের মান আসতে কাজ করে।

def normal(key):
  return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))

-0.9189385

1. log_prob (যেমন প্রোগ্রাম bijective ফাংশন ব্যবহার করে র্যান্ডম variates রুপান্তর থেকে গনা নমুনার লগ-ঘনত্বের সক্ষম হয় jnp.exp , jnp.tanh , jnp.split )।

def log_normal(key):
  return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))

-1.159165

অর্ডার থেকে একটি নমুনা গনা সালে log_normal এর লগ-ঘনত্ব, তাই আমরা প্রথমেই invert করার প্রয়োজনীয়তা exp , গ্রহণ log নমুনা, এবং তারপর ব্যবহার ইনভারস্স লগ-Det Jacobian একটি ভলিউম-পরিবর্তন সংশোধন যোগ exp (দেখুন পরিবর্তন ভেরিয়েবলের উইকিপিডিয়া থেকে সূত্র)।

1. log_prob নমুনা আউটপুট কাঠামো চাই যে প্রোগ্রাম সঙ্গে কাজ, পাইথন অভিধান বা tuples।

def normal_2d(key):
  x = random_variable(
    tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
  x1, x2 = jnp.split(x, 2, 0)
  return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))

{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546

1. log_prob ফাংশনের আঁকা গণনার গ্রাফ পদচারনা, উভয় এগিয়ে এবং বিপরীত মান কম্পিউটিং (এবং তাদের লগ-Det Jacobians) যখন ভেরিয়েবল একটি ভাল-সংজ্ঞায়িত পরিবর্তন মাধ্যমে তাদের বেস নমুনা মান সঙ্গে ফিরে মান সংযোগ স্থাপন করতে একটি প্রয়াস প্রয়োজনীয়। নিম্নলিখিত উদাহরণ প্রোগ্রাম নিন:

def complex_program(key):
  k1, k2 = random.split(key)
  z = random_variable(tfd.Normal(0., 1.))(k1)
  x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
  return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))

(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32))
-1.0967848

এই প্রোগ্রাম, আমরা নমুনা x শর্তসাপেক্ষে উপর z , আমরা অর্থ মূল্য প্রয়োজন z আগে আমরা লগ ঘনত্বের গনা করতে x । যাইহোক, গনা অনুক্রমে z , তাই আমরা প্রথমেই invert আছে jnp.exp প্রয়োগ z । সুতরাং, আদেশের লগ-ঘনত্বের গনা মধ্যে x এবং z , log_prob প্রথম আউটপুট বিপরীতমুখী প্রথম প্রয়োজন, এবং তারপর মাধ্যমে এটি ফরওয়ার্ড পাস jax.nn.relu গড় গনা p(x | z) ।

সম্পর্কে আরও তথ্যের জন্য log_prob , আপনি উল্লেখ করতে পারেন core.interpreters.log_prob । বাস্তবায়ন সালে log_prob ঘনিষ্ঠভাবে দেখা বন্ধ ভিত্তি করে inverse Jax রূপান্তর; সম্পর্কে আরও জানতে inverse দেখতে core.interpreters.inverse ।

joint_sample

আরও জটিল এবং আকর্ষণীয় প্রোগ্রামগুলিকে সংজ্ঞায়িত করতে, আমরা কিছু সুপ্ত র্যান্ডম ভেরিয়েবল ব্যবহার করব, যেমন অপ্রদর্শিত মান সহ র্যান্ডম ভেরিয়েবল। এর পড়ুন যাক latent_normal প্রোগ্রাম যা নমুনার একটি র্যান্ডম মান z যে অন্য র্যান্ডম গড় মান হিসেবে ব্যবহার করা হয় x ।

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

এই প্রোগ্রাম ইন, z প্রচ্ছন্ন তাই আমরা শুধু কল ছিল যদি latent_normal(random.PRNGKey(0)) আমরা প্রকৃত মূল্য জানতাম না z যে জেনারেট করার জন্য দায়ী x ।

joint_sample একটি রূপান্তর যে অন্য প্রোগ্রাম রূপান্তরিত একটি প্রোগ্রাম যা আয় অভিধান ম্যাপিং স্ট্রিং নাম (চিহ্নগুলি) তাদের মান। কাজ করার জন্য, আমাদের নিশ্চিত করতে হবে যে আমরা সুপ্ত ভেরিয়েবলগুলিকে ট্যাগ করেছি যাতে তারা রূপান্তরিত ফাংশনের আউটপুটে উপস্থিত হয়।

joint_sample(latent_normal)(random.PRNGKey(0))

{'x': DeviceArray(0.01873656, dtype=float32),
 'z': DeviceArray(0.14389044, dtype=float32)}

লক্ষ্য করুন joint_sample রূপান্তরগুলির অন্য প্রোগ্রাম মধ্যে একটি প্রোগ্রাম নমুনা তার সুপ্ত মান উপর যৌথ বন্টন, তাই আমরা এটিকে আরো বেশি রুপান্তর করতে পারেন। MCMC এবং VI-এর মতো অ্যালগরিদমগুলির জন্য, অনুমান পদ্ধতির অংশ হিসাবে যৌথ বিতরণের লগ সম্ভাব্যতা গণনা করা সাধারণ। log_prob(latent_normal) না কাজ, কারণ এটা আউট খর্ব করা প্রয়োজন আছে z , কিন্তু আমরা ব্যবহার করতে পারেন log_prob(joint_sample(latent_normal))

print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))

-50.03529
-5049.535

কারণ এই ধরনের একটি সাধারণ প্যাটার্ন, আফ্রিকার একজাতীয় কৃষ্ণসার মৃগ একটি হয়েছে joint_log_prob রূপান্তর যা শুধু রচনা নয় log_prob এবং joint_sample ।

print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))

-50.03529
-5049.535

block

block রূপান্তর একটি প্রোগ্রাম এবং নামের একটি ক্রমানুসারে নেয় এবং একটি প্রোগ্রাম যা অভিন্নরুপে যে স্রোতবরাবর রূপান্তরের (যেমন ছাড়া আচরণ করবে ফেরৎ joint_sample ), প্রদান করা নাম উপেক্ষা করা হয়। যেখানে একটি উদাহরণ block সুবিধাজনক দ্বারা "ব্লক" মান সম্ভাবনা নমুনা সুপ্ত ভেরিয়েবল উপর একটি পূর্বে মধ্যে একটি যৌথ বন্টন রূপান্তর করা হয়। উদাহরণস্বরূপ, নিতে latent_normal , যা প্রথমে একটি স্বপক্ষে z ~ N(0, 1) তারপর x | z ~ N(z, 1e-1) । block(latent_normal, names=['x']) একটি প্রোগ্রাম যা আড়াল করে x নাম, তাই যদি আমরা কি joint_sample(block(latent_normal, names=['x'])) , আমরা শুধু সঙ্গে একটি অভিধান প্রাপ্ত z তাতে .

blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))

{'z': DeviceArray(0.14389044, dtype=float32)}

intervene

intervene বাইরে থেকে মান সঙ্গে সম্ভাব্য প্রোগ্রামে রূপান্তর clobbers নমুনা। আমাদের ফিরে যাওয়া latent_normal প্রোগ্রাম, ধরুন আমরা একই প্রোগ্রাম চালাতে আগ্রহী হয়েছে কিন্তু চেয়েছিলেন দিন z একটি নতুন প্রোগ্রাম লেখার চেয়ে 4. বরং সংশোধন করতে হবে, আমরা ব্যবহার করতে পারি intervene মান ওভাররাইড করতে z ।

intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();

/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

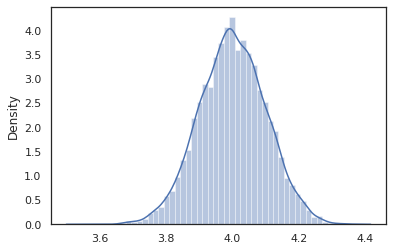
intervened থেকে ফাংশন নমুনা p(x | do(z = 4)) যা শুধু একটি আদর্শ সাধারন বন্টনের 4. কেন্দ্রীভূত আমরা যখন intervene একটি নির্দিষ্ট মূল্যের ওপর, যে মান আর দৈব চলক বিবেচনা করা হয়। এর অর্থ এই যে একটি z মান যখন বাঁধা হবে না নির্বাহ intervened ।

conditional

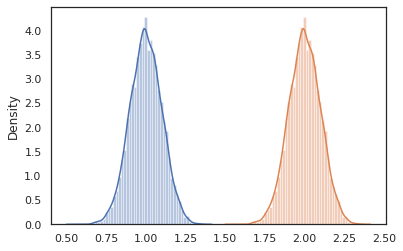
conditional রূপান্তরগুলির একটি প্রোগ্রাম নমুনা এক মধ্যে মান সুপ্ত ঐ সুপ্ত মান উপর শর্ত। আমাদের ফিরে latent_normal প্রোগ্রাম, যা নমুনা p(x) একটি সুপ্ত সঙ্গে z , আমরা এটা একটি শর্তাধীন প্রোগ্রামে রূপান্তর করতে পারেন p(x | z) ।

cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()

99.87485
49.874847
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

nest

যখন আমরা আরও জটিল প্রোগ্রামগুলি তৈরি করার জন্য সম্ভাব্য প্রোগ্রামগুলি রচনা করা শুরু করি, তখন কিছু গুরুত্বপূর্ণ যুক্তিযুক্ত ফাংশনগুলি পুনরায় ব্যবহার করা সাধারণ। উদাহরণস্বরূপ, যদি আমরা একটি Bayesian স্নায়ুর নেটওয়ার্ক গড়ে তুলতে চাই, একটি গুরুত্বপূর্ণ হতে পারে dense প্রোগ্রাম যা নমুনা ওজন ও, executes একটা ফরওয়ার্ড পাস।

আমরা ফাংশন পুনরায় ব্যবহার তবে, আমরা চূড়ান্ত প্রোগ্রাম, যা মত রূপান্তরের দ্বারা অননুমোদিত মধ্যে ডুপ্লিকেট বাঁধা মান দিয়ে শেষ হতে পারে joint_sample । আমরা ব্যবহার করতে পারি nest ট্যাগ তৈরি করতে "সুযোগগুলি" কোথায় একটি নামাঙ্কিত সুযোগ ভেতরে কোনো নমুনা একটি নেস্টেড অভিধান ঢোকানো করা হবে না।

def f(key):
  return random_variable(tfd.Normal(0., 1.), name='x')(key)

def g(key):
  k1, k2 = random.split(key)
  return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))

{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
 'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }

কেস স্টাডি: বায়েসিয়ান নিউরাল নেটওয়ার্ক

আসুন সর্বোত্তম classifying জন্য একটি Bayesian স্নায়ুর নেটওয়ার্ক প্রশিক্ষণ আমাদের হাত চেষ্টা ফিশার আইরিস ডেটা সেটটি। এটি তুলনামূলকভাবে ছোট এবং নিম্ন-মাত্রিক তাই আমরা সরাসরি MCMC এর সাথে পোস্টেরিয়র নমুনা করার চেষ্টা করতে পারি।

প্রথমে, ওরিক্স থেকে ডেটাসেট এবং কিছু অতিরিক্ত ইউটিলিটি আমদানি করা যাক।

from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']

num_features = features.shape[-1]
num_classes = len(iris.target_names)

from oryx.experimental import mcmc
from oryx.util import summary, get_summaries

আমরা একটি ঘন স্তর প্রয়োগ করে শুরু করি, যার ওজন এবং পক্ষপাতের উপর স্বাভাবিক অগ্রাধিকার থাকবে। এই কাজের জন্য, আমরা প্রথমে একটি সংজ্ঞায়িত dense উচ্চতর ক্রম ফাংশন যা কাঙ্ক্ষিত আউটপুট মাত্রা এবং অ্যাক্টিভেশন ফাংশন লাগে। dense ফাংশন একটি সম্ভাব্য প্রোগ্রাম যা একটি শর্তাধীন বিতরণ প্রতিনিধিত্ব করে ফেরৎ p(h | x) যেখানে h একটি ঘন স্তর আউটপুট এবং x তার ইনপুট হয়। এটা প্রথম নমুনার ওজন এবং পক্ষপাত এবং তারপর তাদের ক্ষেত্রে প্রযোজ্য x ।

def dense(dim_out, activation=jax.nn.relu):
  def forward(key, x):
    dim_in = x.shape[-1]
    w_key, b_key = random.split(key)
    w = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
          name='w')(w_key)
    b = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
          name='b')(b_key)
    return activation(jnp.dot(w, x) + b)
  return forward

বিভিন্ন রচনা করতে dense স্তর একসঙ্গে, আমরা একটি বাস্তবায়ন করবে mlp (Multilayer perceptron) উচ্চতর ক্রম ফাংশন যা গোপন আকারের একটি তালিকা শ্রেণীর একটি সংখ্যা লাগে। এটি একটি প্রোগ্রাম যা বারবার আহ্বান ফেরৎ dense উপযুক্ত ব্যবহার hidden_size এবং পরিশেষে চূড়ান্ত স্তর প্রতিটি বর্গ জন্য logits ফেরৎ। উল্লেখ্য ব্যবহার nest যা প্রতিটি স্তরের জন্য নাম সুযোগ সৃষ্টি করে।

def mlp(hidden_sizes, num_classes):
  num_hidden = len(hidden_sizes)
  def forward(key, x):
    keys = random.split(key, num_hidden + 1)
    for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
      x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
    logits = nest(dense(num_classes, activation=lambda x: x),
                  scope=f'layer_{num_hidden + 1}')(keys[-1], x)
    return logits
  return forward

সম্পূর্ণ মডেল বাস্তবায়ন করতে, আমাদের লেবেলগুলিকে শ্রেণীবদ্ধ র্যান্ডম ভেরিয়েবল হিসাবে মডেল করতে হবে। আমরা একটি সংজ্ঞায়িত করব predict ফাংশন যার একটি ডেটাসেটে লাগে xs (বৈশিষ্ট্য) যা পরে একটি মধ্যে গৃহীত হয় mlp ব্যবহার vmap । যখন আমরা ব্যবহার vmap(partial(mlp, mlp_key)) , আমরা ওজন একটি একক সেট নমুনা কিন্তু সমস্ত ইনপুট উপর ফরওয়ার্ড পাস মানচিত্র xs । এই একটি সেট উত্পাদন করে logits যা স্বাধীন শ্রেণীগত ডিস্ট্রিবিউশন parameterizes।

def predict(mlp):
  def forward(key, xs):
    mlp_key, label_key = random.split(key)
    logits = vmap(partial(mlp, mlp_key))(xs)
    return random_variable(
        tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
  return forward

যে পুরো মডেল! প্রদত্ত ডেটা BNN ওজনের পশ্চাৎ অংশের নমুনা করতে MCMC ব্যবহার করা যাক; প্রথমে আমরা ব্যবহার করে একটি বিএনএন "টেমপ্লেট" গঠন করা mlp ।

bnn = mlp([200, 200], num_classes)

আমাদের মার্কভ চেইন জন্য একটি শুরুর স্থান গঠন করা করার জন্য, আমরা ব্যবহার করতে পারেন joint_sample একটি ডামি ইনপুট সঙ্গে।

weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())

dict_keys(['layer_1', 'layer_2', 'layer_3'])

যৌথ বন্টন লগ সম্ভাব্যতা গণনা অনেক অনুমান অ্যালগরিদমের জন্য যথেষ্ট। এখন বলতে আমরা মান্য করা যাক x এবং অবর নমুনা চান p(z | x) । জটিল ডিস্ট্রিবিউশন জন্য, আমরা বাইরে একঘরে করতে সক্ষম নাও হতে হবে x (জন্য যদিও latent_normal কিন্তু আমরা পারি) আমরা একটি unnormalized লগ ঘনত্ব গনা করতে log p(z, x) যেখানে x একটি নির্দিষ্ট মান সংশোধন করা হয়েছে। আমরা পোস্টেরিয়র নমুনা করতে MCMC এর সাথে অস্বাভাবিক লগ সম্ভাব্যতা ব্যবহার করতে পারি। আসুন এই "পিন করা" লগ প্রোব ফাংশনটি লিখি।

def target_log_prob(weights):
  return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)

এখন আমরা ব্যবহার করতে পারেন tfp.mcmc আমাদের unnormalized লগ ঘনত্ব ফাংশন ব্যবহার করে অবর নমুনা। মনে রাখবেন আমরা আমাদের নেস্টেড ওজন একটি "চ্যাপ্টা" সংস্করণ ব্যবহার করতে হবে সঙ্গে সামঞ্জস্যপূর্ণ হতে অভিধানে tfp.mcmc , তাই আমরা Jax গাছ ইউটিলিটি ব্যবহার চেপ্টা এবং unflatten করতে।

@jit
def run_chain(key, weights):
  flat_state, sample_tree = jax.tree_flatten(weights)

  def flat_log_prob(*states):
    return target_log_prob(jax.tree_unflatten(sample_tree, states))

  def trace_fn(_, results):
    return results.inner_results.accepted_results.target_log_prob

  flat_states, log_probs = tfp.mcmc.sample_chain(
    1000,
    num_burnin_steps=9000,
    kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
        tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
        9000, target_accept_prob=0.7),
    trace_fn=trace_fn,
    current_state=flat_state,
    seed=key)
  samples = jax.tree_unflatten(sample_tree, flat_states)
  return samples, log_probs
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)

plt.plot(log_probs)
plt.show()

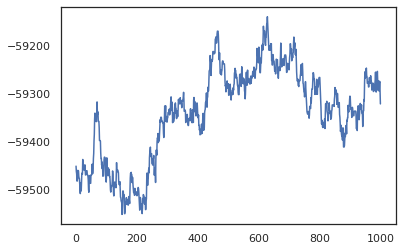
আমরা প্রশিক্ষণের নির্ভুলতার একটি Bayesian মডেল গড় (BMA) অনুমান নিতে আমাদের নমুনাগুলি ব্যবহার করতে পারি। এটা গনা করতে, আমরা ব্যবহার করতে পারেন intervene সঙ্গে bnn বেশী যে কী থেকে নমুনা আমরা সবাই একই জায়গায় "উদ্বুদ্ধ" অবর ওজন হবে। প্রতিটি অবর নমুনা জন্য প্রতিটি ডাটা পয়েন্ট জন্য logits গনা করতে, আমরা দ্বিগুণ করতে পারেন vmap উপর posterior_weights এবং features ।

output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
    random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)

print('Average sample accuracy:', (
    output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
    output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())

Average sample accuracy: 0.9874067
BMA accuracy: 0.99333334

উপসংহার

ওরিক্স-এ, সম্ভাব্য প্রোগ্রামগুলি কেবলমাত্র JAX ফাংশন যা ইনপুট হিসাবে (ছদ্ম-)এলোমেলোতা গ্রহণ করে। JAX-এর ফাংশন ট্রান্সফরমেশন সিস্টেমের সাথে Oryx-এর টাইট ইন্টিগ্রেশনের কারণে, আমরা JAX কোড লেখার মতো সম্ভাব্য প্রোগ্রামগুলি লিখতে এবং ম্যানিপুলেট করতে পারি। এর ফলে জটিল মডেল তৈরি এবং অনুমান করার জন্য একটি সহজ কিন্তু নমনীয় সিস্টেম হয়।