 عرض على TensorFlow.org عرض على TensorFlow.org |  تشغيل في Google Colab تشغيل في Google Colab |  عرض المصدر على جيثب عرض المصدر على جيثب |  تحميل دفتر تحميل دفتر |
pip install -q -U jax jaxlibpip install -q -Uq oryx -Ipip install -q tfp-nightly --upgrade
from functools import partial
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')
import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
import oryx
البرمجة الاحتمالية هي فكرة أنه يمكننا التعبير عن النماذج الاحتمالية باستخدام ميزات من لغة البرمجة. ثم يتم تقديم مهام مثل الاستدلال البايزي أو التهميش كميزات لغوية ويمكن أن تكون آلية.
يوفر Oryx نظام برمجة احتمالي يتم فيه التعبير عن البرامج الاحتمالية فقط كوظائف Python ؛ يتم تحويل هذه البرامج بعد ذلك عبر تحويلات دالة قابلة للتكوين مثل تلك الموجودة في JAX! تكمن الفكرة في البدء ببرامج بسيطة (مثل أخذ عينات من عشوائي عادي) وتكوينها معًا لتشكيل نماذج (مثل شبكة بايز العصبونية). نقطة مهمة من تصميم PPL المها في تمكين البرامج لتبدو وكأنها وظائف كنت إرسال بالفعل واستخدامها في JAX، ولكن توضع حواشي لجعل التحولات على علم بها.
لنقم أولاً باستيراد وظائف Oryx الأساسية PPL.
from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest
ما هي البرامج الاحتمالية في أوريكس؟
في Oryx ، تعد البرامج الاحتمالية مجرد وظائف Python نقية تعمل على قيم JAX ومفاتيح شبه عشوائية وتعيد عينة عشوائية. حسب التصميم، فهي متوافقة مع التحولات مثل jit و vmap . ومع ذلك، يوفر نظام البرمجة احتمالي المها الأدوات التي تمكنك من تعليم وظائف بطرق مفيدة.
وبعد الفلسفة JAX وظائف نقية، برنامج احتمالي أوريكس هي وظيفة بيثون أن يأخذ JAX PRNGKey كأول حجتها وأي عدد من الحجج تكييف اللاحقة. ويسمى الناتج من وظيفة "عينة" ونفس القيود التي تنطبق على jit افتتاحية و vmap تنطبق ظائف افتتاحية لبرامج الاحتمالية (على سبيل المثال لا تعتمد على تدفق البيانات السيطرة، وليس له آثار جانبية، الخ). هذا يختلف عن العديد من أنظمة البرمجة الاحتمالية الحتمية التي تكون فيها "العينة" هي تتبع التنفيذ بالكامل ، بما في ذلك القيم الداخلية لتنفيذ البرنامج. سنرى لاحقا كيف يمكن الوصول المها القيم الداخلية باستخدام joint_sample ، ناقش أدناه.
Program :: PRNGKey -> ... -> Sample
هنا هو برنامج "مرحبا العالم" ان عينات من توزيع السجل العادي .
def log_normal(key):
return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.) 0.8139614 /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
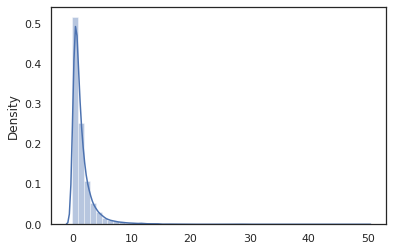
و log_normal الوظيفة هي غلاف رقيق حول Tensorflow الاحتمالية (TFP) التوزيع، ولكن بدلا من استدعاء tfd.Normal(0., 1.).sample ، لقد استخدمت random_variable بدلا من ذلك. كما سنرى لاحقا، random_variable تمكننا من تحويل الأشياء إلى برامج الاحتمالية، جنبا إلى جنب مع وظيفة أخرى مفيدة.
يمكننا تحويل log_normal إلى وظيفة سجل الكثافة باستخدام log_prob التحول:
print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()
-0.9189385
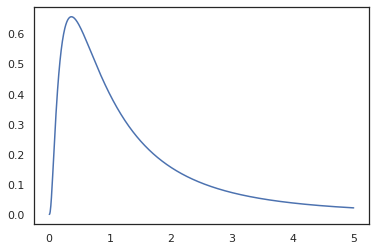
لأننا قد المشروح وظيفة مع random_variable ، log_prob يدرك أن هناك دعوة ل tfd.Normal(0., 1.).sample ويستخدم tfd.Normal(0., 1.).log_prob لحساب توزيع قاعدة مشكلة السجل. للتعامل مع jnp.exp ، ppl.log_prob يحسب تلقائيا الكثافة من خلال وظائف bijective، تتبع التغييرات في الحجم في حساب التغير من بين متغير.
في المها، ويمكن أن نأخذ البرامج وتحويلها باستخدام التحولات وظيفة - على سبيل المثال، jax.jit أو log_prob . ومع ذلك ، لا تستطيع Oryx القيام بذلك مع أي برنامج ؛ يتطلب وظائف أخذ العينات التي سجلت وظيفة كثافة اللوغاريتمات الخاصة بها مع Oryx. لحسن الحظ، المها يسجل تلقائيا TensorFlow احتمال توزيعات (TFP) في نظامها.
أدوات البرمجة الاحتمالية الخاصة بـ Oryx
لدى Oryx العديد من التحولات الوظيفية الموجهة نحو البرمجة الاحتمالية. سنستعرض معظمها ونقدم بعض الأمثلة. في النهاية ، سنجمع كل ذلك معًا في دراسة حالة MCMC. يمكنك أيضا الرجوع إلى وثائق core.ppl.transformations لمزيد من التفاصيل.
random_variable
random_variable فقد اثنين من القطع الرئيسية من وظائف، وتركز على كل من التأشير ظائف بيثون مع المعلومات التي يمكن استخدامها في التحولات.
random_variable"تعمل بوصفها وظيفة هوية افتراضيا، ولكن يمكن استخدام التسجيلات نوع محددة إلى كائنات تحويل إلى programs.` احتماليلأنواع للاستدعاء (وظائف بيثون، lambdas،
functools.partialالصورة، الخ) والتعسفيobjectالصورة (مثل JAXDeviceArrayق) سيكون مجرد العودة مدخلاته.random_variable(x: object) == x random_variable(f: Callable[...]) == fالمها تلقائيا بتسجيل TensorFlow الاحتمالية (TFP) التوزيعات، والتي يتم تحويلها إلى برامج الاحتمالية التي تستدعي توزيع ل
sampleالأسلوب.random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235يقوم Oryx أيضًا بتضمين معلومات حول توزيع TFP في آثار JAX التي تتيح حساب كثافات السجل تلقائيًا.
random_variableالقيم يمكن العلامة مع أسماء، مما يجعلها مفيدة لتحولات المصب، من خلال توفير اختياريnameالحجة الكلمة لrandom_variable. عندما كنا تمرير صفيف إلىrandom_variableجنبا إلى جنب معname(على سبيل المثالrandom_variable(x, name='x'))، انها مجرد علامات قيمة وعوائد ذلك. إذا نحن نمر في استدعاء أو توزيع TFP،random_variableعوائد برنامج أن علامات عينة انتاجها معname.
هذه التعليقات لا تتغير دلالات البرنامج عند تنفيذه، ولكن فقط عندما تتحول (أي البرنامج سيعود نفس القيمة مع أو بدون استخدام random_variable ).
لنستعرض مثالاً نستخدم فيه كلتا الوظيفتين معًا.
def latent_normal(key):
z_key, x_key = random.split(key)
z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)
في هذا البرنامج قمنا المعلمة وسيطة z و x ، مما يجعل التحولات joint_sample ، intervene ، conditional و graph_replace على بينة من الأسماء 'z' و 'x' . سنستعرض بالضبط كيف يستخدم كل تحويل الأسماء لاحقًا.
log_prob
و log_prob تحول وظيفة تحويل برنامج المها احتمالي إلى وظيفة سجل-كثافته. تأخذ دالة كثافة السجل هذه عينة محتملة من البرنامج كمدخلات وترجع كثافة اللوغاريتمات الخاصة بها ضمن توزيع أخذ العينات الأساسي.
log_prob :: Program -> (Sample -> LogDensity)
مثل random_variable ، وأنها تعمل من خلال التسجيل من أنواع حيث سجلت توزيعات TFP تلقائيا، لذلك log_prob(tfd.Normal(0., 1.)) يدعو tfd.Normal(0., 1.).log_prob . لوظائف بيثون، ومع ذلك، log_prob يتتبع البرنامج باستخدام JAX، ويتطلع لأخذ عينات البيانات. و log_prob التحول يعمل على معظم البرامج التي ترجع المتغيرات العشوائية، مباشرة أو عن طريق التحولات للانعكاس ولكن ليس على البرامج التي القيم عينة داخليا التي لم يتم إرجاع. إذا كان لا يمكن عكس العمليات اللازمة في البرنامج، log_prob سوف رمي خطأ.
وفيما يلي بعض الأمثلة على log_prob تطبيقها على مختلف البرامج.
-
log_probيعمل على البرامج التي عينة مباشرة من توزيعات TFP (أو أنواع أخرى مسجلة) والعودة قيمهم.
def normal(key):
return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))
-0.9189385
-
log_probغير قادرة على حساب سجل-كثافة عينات من البرامج التي تحول variates عشوائية باستخدام وظائف bijective (على سبيل المثالjnp.exp،jnp.tanh،jnp.split).
def log_normal(key):
return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))
-1.159165
من أجل حساب عينة من log_normal الصورة سجل الكثافة، نحتاج أولا إلى عكس exp ، مع الأخذ في log من العينة، ثم قم بإضافة تصحيح حجم التغيير باستخدام السجل-ديت معكوس مصفوفه جاكوبي من exp (انظر التغيير من متغير الصيغة من ويكيبيديا).
-
log_probيعمل مع البرامج التي هياكل الانتاج من عينات مثل والقواميس بيثون أو الصفوف.
def normal_2d(key):
x = random_variable(
tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
x1, x2 = jnp.split(x, 2, 0)
return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))
{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546
-
log_probيمشي الرسم البياني حساب تتبع وظيفة، حساب كل من القيم إلى الأمام والعكسية (وسجل-ديت لهم Jacobians) عند الضرورة في محاولة لتوصيل القيم التي يتم إرجاعها مع قاعدة قيمهم عينات عن طريق تغيير محددة جيدا من المتغيرات. خذ المثال التالي من البرنامج:
def complex_program(key):
k1, k2 = random.split(key)
z = random_variable(tfd.Normal(0., 1.))(k1)
x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))
(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32)) -1.0967848
في هذا البرنامج، ونحن عينة x مشروط على z ، وهذا يعني أننا في حاجة إلى قيمة z قبل أن نتمكن من حساب سجل الكثافة من x . ومع ذلك، من أجل حساب z ، علينا أولا أن عكس jnp.exp تطبيقها على z . وهكذا، وذلك لحساب سجل-كثافة x و z ، log_prob احتياجات لأول قلب إخراج الأولى، ومن ثم تمريرها إلى الأمام من خلال jax.nn.relu لحساب متوسط p(x | z) .
لمزيد من المعلومات حول log_prob ، يمكنك الرجوع إلى core.interpreters.log_prob . في التنفيذ، log_prob يستند بشكل وثيق الخروج من inverse تحول JAX. لمعرفة المزيد حول inverse ، انظر core.interpreters.inverse .
joint_sample
لتحديد برامج أكثر تعقيدًا وإثارة للاهتمام ، سنستخدم بعض المتغيرات العشوائية الكامنة ، مثل المتغيرات العشوائية بقيم غير ملحوظة. دعونا تشير إلى latent_normal البرنامج الذي عينات قيمة عشوائي z أن يتم استخدام متوسط قيمة أخرى عشوائي x .
def latent_normal(key):
z_key, x_key = random.split(key)
z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)
في هذا البرنامج، z هو ذلك الكامن إذا كان لنا أن مجرد دعوة latent_normal(random.PRNGKey(0)) ونحن لن نعرف قيمة الفعلية لل z هي المسؤولة عن توليد x .
joint_sample هو التحول الذي يحول البرنامج إلى برنامج آخر أن عائدات القاموس أسماء سلسلة رسم الخرائط (العلامات) إلى قيمها. من أجل العمل ، نحتاج إلى التأكد من وضع علامة على المتغيرات الكامنة للتأكد من ظهورها في إخراج الوظيفة المحولة.
joint_sample(latent_normal)(random.PRNGKey(0))
{'x': DeviceArray(0.01873656, dtype=float32),
'z': DeviceArray(0.14389044, dtype=float32)}
علما بأن joint_sample التحويلات برنامج إلى برنامج آخر أن عينات توزيع مشترك على القيم الكامنة، حتى نتمكن من مواصلة تحويلها. بالنسبة للخوارزميات مثل MCMC و VI ، من الشائع حساب احتمالية سجل التوزيع المشترك كجزء من إجراء الاستدلال. log_prob(latent_normal) لا يعمل لأنه يتطلب تهميش من z ، ولكن يمكننا استخدام log_prob(joint_sample(latent_normal)) .
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))
-50.03529 -5049.535
لأن هذا هو مثل هذا النمط الشائع، وقد أوريكس أيضا joint_log_prob التحول الذي هو مجرد تكوين log_prob و joint_sample .
print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))
-50.03529 -5049.535
block
و block يأخذ التحول في برنامج وسلسلة من أسماء وإرجاع البرنامج الذي يتصرف مماثل إلا أنه في التحولات المصب (مثل joint_sample )، يتم تجاهل الأسماء المقدمة. مثال حيث block هو مفيد وتحويل وتوزيع مشترك إلى قبل أكثر من المتغيرات الكامنة التي كتبها "عرقلة" القيم عينات في احتمال. على سبيل المثال، واتخاذ latent_normal ، الذي يستمد أولا z ~ N(0, 1) بعد ذلك x | z ~ N(z, 1e-1) . block(latent_normal, names=['x']) هو برنامج يخفي x اسم، لذلك اذا لم نفعل joint_sample(block(latent_normal, names=['x'])) ، نحصل على قاموس مع عادل z فيه .
blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))
{'z': DeviceArray(0.14389044, dtype=float32)}
intervene
و intervene clobbers التحول العينات في برنامج احتمالي مع القيم من الخارج. وبالعودة الى لدينا latent_normal البرنامج، دعونا تقول ونحن مهتمون في تشغيل نفس البرنامج ولكن أراد z لتكون ثابتة إلى 4. وبدلا من كتابة برنامج جديد، يمكننا استخدام intervene لتجاوز قيمة z .
intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
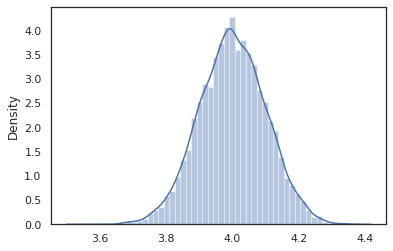
و intervened عينات وظيفة من p(x | do(z = 4)) الذي هو مجرد التوزيع الطبيعي القياسي تركزت في 4. ونحن عندما intervene على قيمة معينة، لم يعد يعتبر أن قيمة المتغير العشوائي. يعني ذلك أن z لن الموسومة قيمة أثناء تنفيذ intervened .
conditional
conditional التحويلات البرنامج الذي عينات الكامنة القيم في واحدة أن الظروف على تلك القيم الكامنة. العودة إلى موقعنا latent_normal البرنامج الذي عينات p(x) مع الكامنة z ، يمكننا تحويله إلى برنامج مشروط p(x | z) .
cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()
99.87485 49.874847 /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning) /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
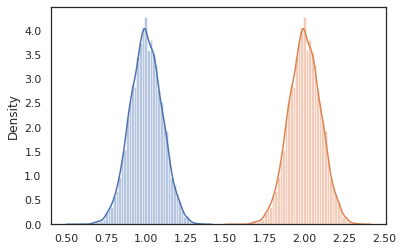
nest
عندما نبدأ في إنشاء برامج احتمالية لبناء برامج أكثر تعقيدًا ، فمن الشائع إعادة استخدام الوظائف التي لها بعض المنطق المهم. على سبيل المثال، إذا كنا نرغب في بناء الشبكة العصبية النظرية الافتراضية، قد يكون هناك المهم dense البرنامج الذي عينات الأوزان وتنفيذ تمريرة إلى الأمام.
إذا كان لنا أن إعادة وظائف، ومع ذلك، فإننا قد ينتهي مع القيم الموسومة مكررة في البرنامج النهائي، الذي ألغي من قبل التحولات مثل joint_sample . يمكننا استخدام nest لإنشاء سمة "نطاقات"، حيث سيتم إدراج أي عينات من داخل نطاق اسمه في القاموس متداخلة.
def f(key):
return random_variable(tfd.Normal(0., 1.), name='x')(key)
def g(key):
k1, k2 = random.split(key)
return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))
{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }
دراسة حالة: شبكة بايزي العصبية
دعونا نحاول يدنا في تدريب الشبكة العصبية النظرية الافتراضية لتصنيف الكلاسيكية فيشر ايريس البيانات. إنه صغير نسبيًا ومنخفض الأبعاد ، لذا يمكننا محاولة أخذ عينات مباشرة مع MCMC.
أولاً ، دعنا نستورد مجموعة البيانات وبعض الأدوات المساعدة الإضافية من Oryx.
from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
from oryx.experimental import mcmc
from oryx.util import summary, get_summaries
نبدأ بتنفيذ طبقة كثيفة ، والتي سيكون لها مقدمات عادية على الأوزان والتحيز. للقيام بذلك، علينا أولا تحديد dense أعلى وظيفة من أجل أن يأخذ في البعد الانتاج وتفعيل الوظيفة المطلوبة. و dense ترجع برنامج الاحتمالي الذي يمثل توزيع مشروط p(h | x) حيث h هو إخراج طبقة كثيفة و x هو مدخلاته. هذه أول عينات الوزن والتحيز ومن ثم تنطبق عليهم x .
def dense(dim_out, activation=jax.nn.relu):
def forward(key, x):
dim_in = x.shape[-1]
w_key, b_key = random.split(key)
w = random_variable(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
name='w')(w_key)
b = random_variable(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
name='b')(b_key)
return activation(jnp.dot(w, x) + b)
return forward
أن يؤلف عدة dense طبقات معا، ونحن سوف تنفيذ mlp (متعدد الطبقات المستقبلات) أعلى وظيفة النظام الذي يأخذ في قائمة أحجام الخفية وعدد من الطبقات. تقوم بإرجاع البرنامج الذي يدعو مرارا وتكرارا dense استخدام المناسب hidden_size وأخيرا يعود logits لكل فئة في الطبقة النهائية. لاحظ استخدام nest الذي يخلق نطاقات اسم كل طبقة.
def mlp(hidden_sizes, num_classes):
num_hidden = len(hidden_sizes)
def forward(key, x):
keys = random.split(key, num_hidden + 1)
for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
logits = nest(dense(num_classes, activation=lambda x: x),
scope=f'layer_{num_hidden + 1}')(keys[-1], x)
return logits
return forward
لتنفيذ النموذج الكامل ، سنحتاج إلى نمذجة التسميات كمتغيرات عشوائية فئوية. سنقوم بتعريف predict وظيفة التي تأخذ في مجموعة بيانات من xs (ملامح) التي مرت بعد ذلك إلى mlp باستخدام vmap . عندما نستخدم vmap(partial(mlp, mlp_key)) ، ونحن تذوق مجموعة واحدة من الأوزان، ولكن الخريطة الممر إلى الأمام على جميع مدخلات xs . هذا وتنتج مجموعة من logits التي parameterizes توزيعات القاطع مستقلة.
def predict(mlp):
def forward(key, xs):
mlp_key, label_key = random.split(key)
logits = vmap(partial(mlp, mlp_key))(xs)
return random_variable(
tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
return forward
هذا هو النموذج الكامل! دعنا نستخدم MCMC لأخذ عينات لاحقة من أوزان BNN المعطاة للبيانات ؛ أولا نحن بناء BNN "قالب" باستخدام mlp .
bnn = mlp([200, 200], num_classes)
لإنشاء نقطة الانطلاق لدينا سلسلة ماركوف، يمكننا استخدام joint_sample مع المدخلات وهمية.
weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())
dict_keys(['layer_1', 'layer_2', 'layer_3'])
يعد حساب احتمال سجل التوزيع المشترك كافياً للعديد من خوارزميات الاستدلال. دعونا يقول الآن نلاحظ x وتريد لأخذ عينات من الخلفي p(z | x) . لتوزيعات معقدة، ونحن لن تكون قادرة على تهميش من x (على الرغم من ل latent_normal نستطيع) ولكن يمكننا حساب لunnormalized كثافة سجل log p(z, x) حيث x هو ثابت لقيمة معينة. يمكننا استخدام احتمالية السجل غير الطبيعي مع MCMC لأخذ عينات لاحقة. دعونا نكتب هذه الوظيفة "المثبتة" السجل.
def target_log_prob(weights):
return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)
الآن يمكننا استخدام tfp.mcmc لأخذ عينات من الخلفي باستخدام لدينا unnormalized دالة الكثافة السجل. علما بأن علينا أن استخدام "المسطحة" نسخة من الأوزان المتداخلة لدينا قاموس لتكون متوافقة مع tfp.mcmc ، لذلك نستخدم المرافق شجرة JAX للشد وunflatten.
@jit
def run_chain(key, weights):
flat_state, sample_tree = jax.tree_flatten(weights)
def flat_log_prob(*states):
return target_log_prob(jax.tree_unflatten(sample_tree, states))
def trace_fn(_, results):
return results.inner_results.accepted_results.target_log_prob
flat_states, log_probs = tfp.mcmc.sample_chain(
1000,
num_burnin_steps=9000,
kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
9000, target_accept_prob=0.7),
trace_fn=trace_fn,
current_state=flat_state,
seed=key)
samples = jax.tree_unflatten(sample_tree, flat_states)
return samples, log_probs
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)
plt.plot(log_probs)
plt.show()
يمكننا استخدام عيناتنا لأخذ تقدير متوسط نموذج بايزي (BMA) لدقة التدريب. لحساب ذلك، يمكننا استخدام intervene مع bnn إلى "حقن" الخلفي الأوزان بدلا من تلك التي يتم أخذ عينات من المفتاح. لحساب logits لكل نقطة بيانات لكل عينة الخلفية، يمكننا مضاعفة vmap على posterior_weights و features .
output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)
print('Average sample accuracy:', (
output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())
Average sample accuracy: 0.9874067 BMA accuracy: 0.99333334
استنتاج
في Oryx ، تعد البرامج الاحتمالية مجرد وظائف JAX التي تأخذ العشوائية (الزائفة) كمدخل. بسبب تكامل Oryx الضيق مع نظام تحويل الوظائف في JAX ، يمكننا كتابة ومعالجة البرامج الاحتمالية كما نكتب كود JAX. ينتج عن هذا نظام بسيط ولكنه مرن لبناء نماذج معقدة والقيام بالاستدلال.
