 Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
Suy luận biến đổi (VI) sử dụng suy luận Bayes gần đúng như một bài toán tối ưu hóa và tìm kiếm phân phối hậu nghiệm 'thay thế' để giảm thiểu sự phân kỳ KL với hậu nghiệm thực sự. VI dựa trên Gradient thường nhanh hơn các phương pháp MCMC, soạn thảo tự nhiên với việc tối ưu hóa các tham số mô hình và cung cấp giới hạn thấp hơn về bằng chứng mô hình có thể được sử dụng trực tiếp để so sánh mô hình, chẩn đoán hội tụ và suy luận có thể tổng hợp.
TensorFlow Probability cung cấp các công cụ cho VI nhanh chóng, linh hoạt và có thể mở rộng, phù hợp một cách tự nhiên với ngăn xếp TFP. Những công cụ này cho phép xây dựng các mã hậu đại thay thế với cấu trúc hiệp phương sai được tạo ra bởi các phép biến đổi tuyến tính hoặc chuẩn hóa các luồng.
VI có thể được sử dụng để ước Bayesian khoảng đáng tin cậy cho các thông số của một mô hình hồi quy để ước tính ảnh hưởng của phương pháp điều trị khác nhau hoặc các tính năng quan sát trên một kết quả của sự quan tâm. Các khoảng đáng tin cậy ràng buộc các giá trị của một tham số không được quan sát với một xác suất nhất định, theo phân phối sau của tham số được điều kiện dựa trên dữ liệu quan sát và đưa ra một giả định về phân phối trước của tham số.
Trong Colab này, chúng tôi chứng minh làm thế nào để sử dụng VI để có được những khoảng thời gian đáng tin cậy cho các thông số của một Bayesian tuyến tính mô hình hồi quy cho các mức độ radon đo trong nhà (sử dụng Gelman et al (2007) Radon tập dữ liệu. , Xem ví dụ tương tự trong Stan). Chúng tôi chứng minh như thế nào TFP JointDistribution s kết hợp với bijectors để xây dựng và phù hợp với hai loại posteriors thay thế biểu cảm:
- một tiêu chuẩn Phân phối chuẩn được biến đổi bởi một ma trận khối. Ma trận có thể phản ánh sự độc lập giữa một số thành phần của hậu phương và sự phụ thuộc giữa những thành phần khác, làm giảm bớt giả định về trường trung bình hoặc hiệp phương sai đầy đủ.
- một phức tạp hơn, dung lượng cao hơn ngược dòng chảy tự hồi quy .
Các nhân viên phụ trách đại diện được đào tạo và so sánh với các kết quả từ đường cơ sở sau đại diện trường trung bình, cũng như các mẫu sự thật cơ bản từ Hamiltonian Monte Carlo.
Tổng quan về Suy luận Biến đổi Bayes
Giả sử chúng ta có quá trình sinh sản sau đây, nơi \(\theta\) đại diện cho các thông số ngẫu nhiên, \(\omega\) đại diện cho các thông số xác định, và \(x_i\) là các tính năng và \(y_i\) là những giá trị mục tiêu cho \(i=1,\ldots,n\) quan sát dữ liệu điểm: \ begin {class } & \ theta \ sim r (\ Theta) && \ text {(Trước đó)} \ & \ text {for} i = 1 \ ldots n: \ nonumber \ & \ quad y_i \ sim p (Y_i | x_i, \ theta , \ omega) && \ text {(Khả năng)} \ end {class}
VI sau đó được đặc trưng bởi: $ \ newcommand {\ E} {\ operatorname {\ mathbb {E}}} \ newcommand {\ K} {\ operatorname {\ mathbb {K}}} \ newcommand {\ defeq} {\ overset {\ tiny \ text {def}} {=}} \ DeclareMathOperator * {\ argmin} {arg \, min} $
\ begin {class} - \ log p ({y_i} _i ^ n | {x_i} _i ^ n, \ omega) & \ defeq - \ log \ int \ textrm {d} \ theta \, r (\ theta) \ prod_i ^ np (y_i | x_i, \ theta, \ omega) && \ text {(Tích phân thực sự khó)} \ & = - \ log \ int \ textrm {d} \ theta \, q (\ theta) \ frac {1 } {q (\ theta)} r (\ theta) \ prod_i ^ np (y_i | x_i, \ theta, \ omega) && \ text {(Nhân với 1)} \ & \ le - \ int \ textrm {d} \ theta \, q (\ theta) \ log \ frac {r (\ theta) \ prod_i ^ np (y_i | x i, \ theta, \ omega)} {q (\ theta)} && \ text {(Bất đẳng thức Jensen )} \ & \ defeq \ E {q (\ Theta)} [- \ log p (y_i | x_i, \ Theta, \ omega)] + \ K [q (\ Theta), r (\ Theta)] \ & \ defeq \text{expected negative log likelihood"} + \ text {kl regularizer"} \ end {class}
(Về mặt kỹ thuật chúng ta đang giả định \(q\) là hoàn toàn liên tục đối với với \(r\). Xem thêm, Bất đẳng thức Jensen .)
Vì giới hạn giữ cho tất cả q, nên rõ ràng nó là chặt chẽ nhất đối với:
\[q^*,w^* = \argmin_{q \in \mathcal{Q},\omega\in\mathbb{R}^d} \left\{ \sum_i^n\E_{q(\Theta)}\left[ -\log p(y_i|x_i,\Theta, \omega) \right] + \K[q(\Theta), r(\Theta)] \right\}\]
Về thuật ngữ, chúng tôi gọi là
- \(q^*\) các "sau thay thế," và,
- \(\mathcal{Q}\) các "đại diện gia đình."
\(\omega^*\) đại diện cho các giá trị tối đa-khả năng các thông số xác định trên sự mất mát VI. Xem cuộc khảo sát này để biết thêm thông tin về suy luận biến phân.
Ví dụ: Hồi quy tuyến tính phân cấp Bayes trên các phép đo Radon
Radon là một loại khí phóng xạ xâm nhập vào nhà thông qua các điểm tiếp xúc với mặt đất. Nó là một chất gây ung thư là nguyên nhân chính gây ung thư phổi ở những người không hút thuốc. Mức độ radon khác nhau rất nhiều giữa các hộ gia đình.
EPA đã thực hiện một nghiên cứu về mức radon trong 80.000 ngôi nhà. Hai yếu tố dự báo quan trọng là:
- Tầng mà phép đo được thực hiện (radon cao hơn ở tầng hầm)
- Mức uranium của hạt (tương quan thuận với mức radon)
Dự đoán mức độ radon trong nhà được phân nhóm theo quận là một vấn đề kinh điển trong mô hình thứ bậc Bayesian, được giới thiệu bởi Gelman và Hill (2006) . Chúng tôi sẽ xây dựng một mô hình tuyến tính phân cấp để dự đoán các phép đo radon trong các ngôi nhà, trong đó phân cấp là nhóm các ngôi nhà theo quận. Chúng tôi quan tâm đến khoảng thời gian đáng tin cậy đối với ảnh hưởng của vị trí (quận) đối với mức radon của các ngôi nhà ở Minnesota. Để cô lập hiệu ứng này, ảnh hưởng của tầng và mức uranium cũng được đưa vào mô hình. Ngoài ra, chúng tôi sẽ kết hợp hiệu ứng theo ngữ cảnh tương ứng với tầng trung bình mà phép đo được thực hiện, theo hạt, để nếu có sự khác biệt giữa các hạt của tầng mà các phép đo được thực hiện, thì điều này không được quy cho hiệu ứng của hạt.
pip3 install -q tf-nightly tfp-nightly
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow as tf
import tensorflow_datasets as tfds
import tensorflow_probability as tfp
import warnings
tfd = tfp.distributions
tfb = tfp.bijectors
plt.rcParams['figure.facecolor'] = '1.'
# Load the Radon dataset from `tensorflow_datasets` and filter to data from
# Minnesota.
dataset = tfds.as_numpy(
tfds.load('radon', split='train').filter(
lambda x: x['features']['state'] == 'MN').batch(10**9))
# Dependent variable: Radon measurements by house.
dataset = next(iter(dataset))
radon_measurement = dataset['activity'].astype(np.float32)
radon_measurement[radon_measurement <= 0.] = 0.1
log_radon = np.log(radon_measurement)
# Measured uranium concentrations in surrounding soil.
uranium_measurement = dataset['features']['Uppm'].astype(np.float32)
log_uranium = np.log(uranium_measurement)
# County indicator.
county_strings = dataset['features']['county'].astype('U13')
unique_counties, county = np.unique(county_strings, return_inverse=True)
county = county.astype(np.int32)
num_counties = unique_counties.size
# Floor on which the measurement was taken.
floor_of_house = dataset['features']['floor'].astype(np.int32)
# Average floor by county (contextual effect).
county_mean_floor = []
for i in range(num_counties):
county_mean_floor.append(floor_of_house[county == i].mean())
county_mean_floor = np.array(county_mean_floor, dtype=log_radon.dtype)
floor_by_county = county_mean_floor[county]
Mô hình hồi quy được xác định như sau:
\(\newcommand{\Normal}{\operatorname{\sf Normal} }\)\ begin {class} & \ text {uranium_weight} \ sim \ Bình thường (0, 1) \ & \ text {county_floor_weight} \ sim \ Bình thường (0, 1) \ & \ text {for} j = 1 \ ldots \ text {num_counties}: \ & \ quad \ text {county_effect} _j \ sim \ Normal (0, \ sigma_c) \ & \ text {for} i = 1 \ ldots n: \ & \ quad \ mu_i = (\ & \ quad \ quad \ text {thiên vị} \ & \ quad \ quad + \ text {hiệu lực quận} {\ text {quận} _i} \ & \ quad \ quad + \ text {log_uranium} _i \ times \ text {uranium_weight } \ & \ quad \ quad + \ text {floor_of_house} _i \ times \ text {floor_weight} \ & \ quad \ quad + \ text {floor_by quận} {\ text {quận} _i} \ times \ text {county_floor_weight}) \ & \ quad \ text {log_radon} _i \ sim \ Bình thường (\ mu_i, \ sigma_y) \ end {class} trong đó \(i\) chỉ số quan sát và \(\text{county}_i\) là quận trong đó \(i\)thứ quan sát được Lấy.
Chúng tôi sử dụng hiệu ứng ngẫu nhiên cấp hạt để nắm bắt sự khác biệt về địa lý. Các thông số uranium_weight và county_floor_weight được mô hình hóa xác suất, và floor_weight và hằng số bias là xác định. Các lựa chọn mô hình này phần lớn là tùy ý và được thực hiện với mục đích chứng minh VI trên một mô hình xác suất có độ phức tạp hợp lý. Đối với một cuộc thảo luận kỹ hơn về mô hình đa cấp với các hiệu ứng cố định và ngẫu nhiên trong TFP, sử dụng dữ liệu radon, xem đa cấp Modeling Primer và Lắp Generalized tuyến tính hỗn hợp tác dụng Models Sử dụng biến phân suy luận .
# Create variables for fixed effects.
floor_weight = tf.Variable(0.)
bias = tf.Variable(0.)
# Variables for scale parameters.
log_radon_scale = tfp.util.TransformedVariable(1., tfb.Exp())
county_effect_scale = tfp.util.TransformedVariable(1., tfb.Exp())
# Define the probabilistic graphical model as a JointDistribution.
@tfd.JointDistributionCoroutineAutoBatched
def model():
uranium_weight = yield tfd.Normal(0., scale=1., name='uranium_weight')
county_floor_weight = yield tfd.Normal(
0., scale=1., name='county_floor_weight')
county_effect = yield tfd.Sample(
tfd.Normal(0., scale=county_effect_scale),
sample_shape=[num_counties], name='county_effect')
yield tfd.Normal(
loc=(log_uranium * uranium_weight + floor_of_house* floor_weight
+ floor_by_county * county_floor_weight
+ tf.gather(county_effect, county, axis=-1)
+ bias),
scale=log_radon_scale[..., tf.newaxis],
name='log_radon')
# Pin the observed `log_radon` values to model the un-normalized posterior.
target_model = model.experimental_pin(log_radon=log_radon)
Người đưa thư đại diện biểu cảm
Tiếp theo, chúng tôi ước tính các phân phối sau của các hiệu ứng ngẫu nhiên bằng cách sử dụng VI với hai loại hậu quả thay thế khác nhau:
- Một phân phối Chuẩn đa biến bị ràng buộc, với cấu trúc hiệp phương sai được tạo ra bởi phép biến đổi ma trận theo khối.
- Một phân phối tiêu chuẩn bình thường đa biến biến đổi bởi một Inverse autoregressive dòng chảy , sau đó được tách ra và tái cơ cấu để phù hợp với sự hỗ trợ của sau.
Đa biến Bình thường thay thế hậu sau
Để xây dựng phần sau thay thế này, một toán tử tuyến tính có thể huấn luyện được sử dụng để tạo ra mối tương quan giữa các thành phần của phần sau.
# Determine the `event_shape` of the posterior, and calculate the size of each
# `event_shape` component. These determine the sizes of the components of the
# underlying standard Normal distribution, and the dimensions of the blocks in
# the blockwise matrix transformation.
event_shape = target_model.event_shape_tensor()
flat_event_shape = tf.nest.flatten(event_shape)
flat_event_size = tf.nest.map_structure(tf.reduce_prod, flat_event_shape)
# The `event_space_bijector` maps unconstrained values (in R^n) to the support
# of the prior -- we'll need this at the end to constrain Multivariate Normal
# samples to the prior's support.
event_space_bijector = target_model.experimental_default_event_space_bijector()
Xây dựng một JointDistribution với các thành phần thông thường tiêu chuẩn vector có giá trị, với kích thước xác định bởi các thành phần trước tương ứng. Các thành phần phải có giá trị vectơ để chúng có thể được biến đổi bởi toán tử tuyến tính.
base_standard_dist = tfd.JointDistributionSequential(
[tfd.Sample(tfd.Normal(0., 1.), s) for s in flat_event_size])
Xây dựng một toán tử tuyến tính tam giác dưới theo khối có thể huấn luyện được. Chúng tôi sẽ áp dụng nó cho phân phối Chuẩn chuẩn để thực hiện một phép biến đổi ma trận khối (có thể huấn luyện) và tạo ra cấu trúc tương quan của phần sau.
Trong điều hành blockwise tuyến tính, một khối đầy đủ ma trận khả năng huấn luyện đại diện hiệp phương sai đầy đủ giữa hai thành phần của sau, trong khi một khối số không (hoặc None ) thể hiện sự độc lập. Các khối trên đường chéo là ma trận tam giác dưới hoặc đường chéo, để toàn bộ cấu trúc khối biểu diễn một ma trận tam giác dưới.
Việc áp dụng bijector này vào phân phối cơ sở dẫn đến phân phối Chuẩn đa biến với phương sai trung bình 0 và (Cholesky-nhân tố) bằng với ma trận khối tam giác dưới.
operators = (
(tf.linalg.LinearOperatorDiag,), # Variance of uranium weight (scalar).
(tf.linalg.LinearOperatorFullMatrix, # Covariance between uranium and floor-by-county weights.
tf.linalg.LinearOperatorDiag), # Variance of floor-by-county weight (scalar).
(None, # Independence between uranium weight and county effects.
None, # Independence between floor-by-county and county effects.
tf.linalg.LinearOperatorDiag) # Independence among the 85 county effects.
)
block_tril_linop = (
tfp.experimental.vi.util.build_trainable_linear_operator_block(
operators, flat_event_size))
scale_bijector = tfb.ScaleMatvecLinearOperatorBlock(block_tril_linop)
Sau khi áp dụng các toán tử tuyến tính để phân phối bình thường tiêu chuẩn, áp dụng một nhiều phần dữ liệu Shift bijector để cho phép giá trị trung bình để có giá trị khác không.
loc_bijector = tfb.JointMap(
tf.nest.map_structure(
lambda s: tfb.Shift(
tf.Variable(tf.random.uniform(
(s,), minval=-2., maxval=2., dtype=tf.float32))),
flat_event_size))
Phân phối Chuẩn đa biến thu được, thu được bằng cách biến đổi phân phối Chuẩn với các bijector tỷ lệ và vị trí, phải được định hình lại và cấu trúc lại để phù hợp với phân phối trước và cuối cùng bị hạn chế bởi sự hỗ trợ của phân phối trước.
# Reshape each component to match the prior, using a nested structure of
# `Reshape` bijectors wrapped in `JointMap` to form a multipart bijector.
reshape_bijector = tfb.JointMap(
tf.nest.map_structure(tfb.Reshape, flat_event_shape))
# Restructure the flat list of components to match the prior's structure
unflatten_bijector = tfb.Restructure(
tf.nest.pack_sequence_as(
event_shape, range(len(flat_event_shape))))
Bây giờ, hãy tập hợp tất cả lại với nhau - chuỗi các bijector có thể huấn luyện lại với nhau và áp dụng chúng vào tiêu chuẩn cơ sở Phân phối chuẩn để tạo ra phần sau thay thế.
surrogate_posterior = tfd.TransformedDistribution(
base_standard_dist,
bijector = tfb.Chain( # Note that the chained bijectors are applied in reverse order
[
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the posterior
reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
loc_bijector, # allow for nonzero mean
scale_bijector # apply the block matrix transformation to the standard Normal distribution
]))
Huấn luyện hậu kỳ đại diện thay thế bình thường đa biến.
optimizer = tf.optimizers.Adam(learning_rate=1e-2)
mvn_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=16,
jit_compile=True)
mvn_samples = surrogate_posterior.sample(1000)
mvn_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*mvn_samples)
- surrogate_posterior.log_prob(mvn_samples))
print('Multivariate Normal surrogate posterior ELBO: {}'.format(mvn_final_elbo))
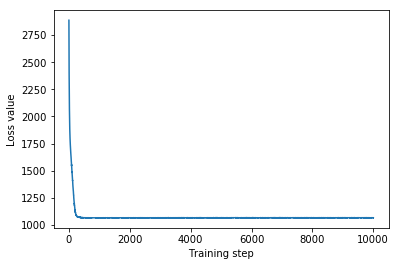
plt.plot(mvn_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
Multivariate Normal surrogate posterior ELBO: -1065.705322265625
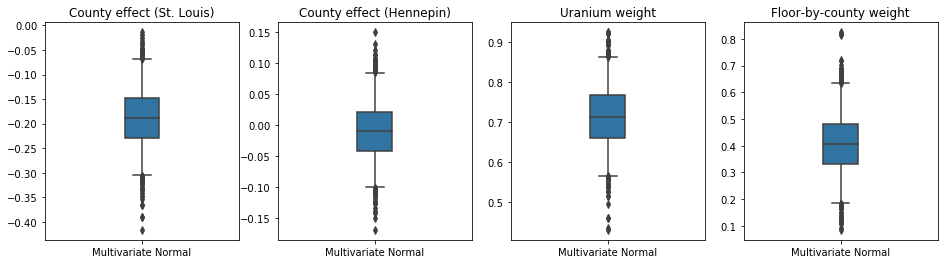
Vì phần sau đại diện được đào tạo là một phân phối TFP, chúng tôi có thể lấy mẫu từ đó và xử lý chúng để tạo ra khoảng tin cậy sau cho các tham số.
Hộp-and-râu lô dưới đây cho thấy 50% và 95% khoảng thời gian đáng tin cậy cho các hiệu ứng hạt hai quận lớn nhất và trọng lượng hồi quy trên các phép đo uranium đất và sàn trung bình của quận. Khoảng thời gian đáng tin cậy sau đối với ảnh hưởng của hạt chỉ ra rằng vị trí ở hạt St. Louis có liên quan đến mức radon thấp hơn, sau khi tính đến các biến số khác, và ảnh hưởng của vị trí ở hạt Hennepin là gần trung lập.
Khoảng tin cậy sau cùng trên trọng số hồi quy cho thấy rằng các mức uranium trong đất cao hơn có liên quan đến mức radon cao hơn và các hạt nơi phép đo được thực hiện ở các tầng cao hơn (có thể vì ngôi nhà không có tầng hầm) có xu hướng có mức radon cao hơn, có thể liên quan đến các đặc tính của đất và ảnh hưởng của chúng đến loại công trình được xây dựng.
Hệ số (xác định) của tầng là âm, cho thấy rằng các tầng thấp hơn có mức radon cao hơn, như mong đợi.
st_louis_co = 69 # Index of St. Louis, the county with the most observations.
hennepin_co = 25 # Index of Hennepin, with the second-most observations.
def pack_samples(samples):
return {'County effect (St. Louis)': samples.county_effect[..., st_louis_co],
'County effect (Hennepin)': samples.county_effect[..., hennepin_co],
'Uranium weight': samples.uranium_weight,
'Floor-by-county weight': samples.county_floor_weight}
def plot_boxplot(posterior_samples):
fig, axes = plt.subplots(1, 4, figsize=(16, 4))
# Invert the results dict for easier plotting.
k = list(posterior_samples.values())[0].keys()
plot_results = {
v: {p: posterior_samples[p][v] for p in posterior_samples} for v in k}
for i, (var, var_results) in enumerate(plot_results.items()):
sns.boxplot(data=list(var_results.values()), ax=axes[i],
width=0.18*len(var_results), whis=(2.5, 97.5))
# axes[i].boxplot(list(var_results.values()), whis=(2.5, 97.5))
axes[i].title.set_text(var)
fs = 10 if len(var_results) < 4 else 8
axes[i].set_xticklabels(list(var_results.keys()), fontsize=fs)
results = {'Multivariate Normal': pack_samples(mvn_samples)}
print('Bias is: {:.2f}'.format(bias.numpy()))
print('Floor fixed effect is: {:.2f}'.format(floor_weight.numpy()))
plot_boxplot(results)
Bias is: 1.40 Floor fixed effect is: -0.72
Ngược dòng tự động hồi quy ngược dòng thay thế phía sau
Luồng tự động phục hồi nghịch đảo (IAF) đang chuẩn hóa các luồng sử dụng mạng nơ-ron để nắm bắt các phụ thuộc phi tuyến, phức tạp giữa các thành phần của phân phối. Tiếp theo, chúng tôi xây dựng hậu trường đại diện IAF để xem liệu mô hình có dung lượng cao hơn, khả thi hơn này có hoạt động tốt hơn so với Chuẩn đa biến bị ràng buộc hay không.
# Build a standard Normal with a vector `event_shape`, with length equal to the
# total number of degrees of freedom in the posterior.
base_distribution = tfd.Sample(
tfd.Normal(0., 1.), sample_shape=[tf.reduce_sum(flat_event_size)])
# Apply an IAF to the base distribution.
num_iafs = 2
iaf_bijectors = [
tfb.Invert(tfb.MaskedAutoregressiveFlow(
shift_and_log_scale_fn=tfb.AutoregressiveNetwork(
params=2, hidden_units=[256, 256], activation='relu')))
for _ in range(num_iafs)
]
# Split the base distribution's `event_shape` into components that are equal
# in size to the prior's components.
split = tfb.Split(flat_event_size)
# Chain these bijectors and apply them to the standard Normal base distribution
# to build the surrogate posterior. `event_space_bijector`,
# `unflatten_bijector`, and `reshape_bijector` are the same as in the
# multivariate Normal surrogate posterior.
iaf_surrogate_posterior = tfd.TransformedDistribution(
base_distribution,
bijector=tfb.Chain([
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the prior
reshape_bijector, # reshape the vector-valued components to match the shapes of the prior components
split] + # Split the samples into components of the same size as the prior components
iaf_bijectors # Apply a flow model to the Tensor-valued standard Normal distribution
))
Huấn luyện hậu nhân đại diện của IAF.
optimizer=tf.optimizers.Adam(learning_rate=1e-2)
iaf_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
iaf_surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=4,
jit_compile=True)
iaf_samples = iaf_surrogate_posterior.sample(1000)
iaf_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*iaf_samples)
- iaf_surrogate_posterior.log_prob(iaf_samples))
print('IAF surrogate posterior ELBO: {}'.format(iaf_final_elbo))
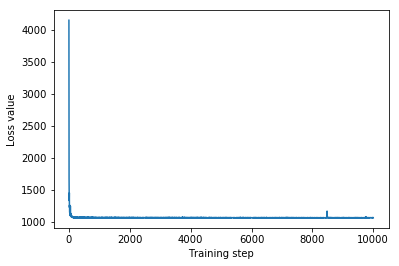
plt.plot(iaf_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
IAF surrogate posterior ELBO: -1065.3663330078125
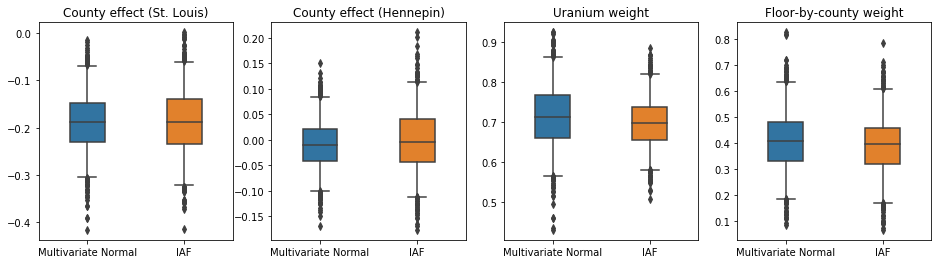
Các khoảng đáng tin cậy cho phần sau đại diện của IAF xuất hiện tương tự như khoảng thời gian của Chuẩn đa biến bị ràng buộc.
results['IAF'] = pack_samples(iaf_samples)
plot_boxplot(results)
Đường cơ sở: Hậu quả đại diện trường trung bình
VI sau thay thế thường được giả định là trường trung bình (độc lập) Các phân phối chuẩn, với các phương tiện và phương sai có thể huấn luyện được, được giới hạn bởi sự hỗ trợ của cái trước bằng một phép biến đổi mang tính khách quan. Chúng tôi xác định phần sau đại diện trường trung bình ngoài hai phần sau đại diện biểu cảm hơn, sử dụng cùng một công thức chung như phần sau đại diện Bình thường đa biến.
# A block-diagonal linear operator, in which each block is a diagonal operator,
# transforms the standard Normal base distribution to produce a mean-field
# surrogate posterior.
operators = (tf.linalg.LinearOperatorDiag,
tf.linalg.LinearOperatorDiag,
tf.linalg.LinearOperatorDiag)
block_diag_linop = (
tfp.experimental.vi.util.build_trainable_linear_operator_block(
operators, flat_event_size))
mean_field_scale = tfb.ScaleMatvecLinearOperatorBlock(block_diag_linop)
mean_field_loc = tfb.JointMap(
tf.nest.map_structure(
lambda s: tfb.Shift(
tf.Variable(tf.random.uniform(
(s,), minval=-2., maxval=2., dtype=tf.float32))),
flat_event_size))
mean_field_surrogate_posterior = tfd.TransformedDistribution(
base_standard_dist,
bijector = tfb.Chain( # Note that the chained bijectors are applied in reverse order
[
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the posterior
reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
mean_field_loc, # allow for nonzero mean
mean_field_scale # apply the block matrix transformation to the standard Normal distribution
]))
optimizer=tf.optimizers.Adam(learning_rate=1e-2)
mean_field_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
mean_field_surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=16,
jit_compile=True)
mean_field_samples = mean_field_surrogate_posterior.sample(1000)
mean_field_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*mean_field_samples)
- mean_field_surrogate_posterior.log_prob(mean_field_samples))
print('Mean-field surrogate posterior ELBO: {}'.format(mean_field_final_elbo))
plt.plot(mean_field_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
Mean-field surrogate posterior ELBO: -1065.7652587890625
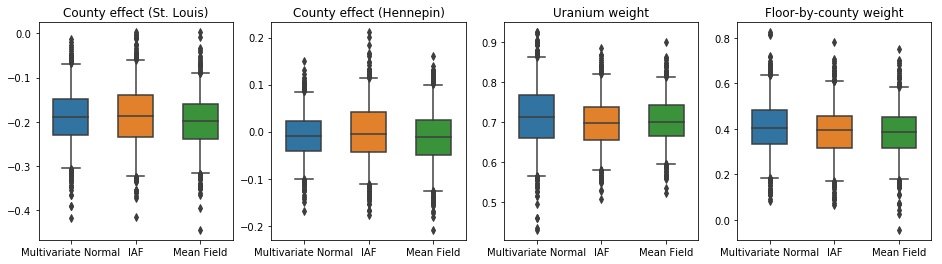
Trong trường hợp này, phần sau đại diện trường trung bình cho kết quả tương tự với phần sau đại diện biểu cảm hơn, cho thấy rằng mô hình đơn giản hơn này có thể thích hợp cho nhiệm vụ suy luận.
results['Mean Field'] = pack_samples(mean_field_samples)
plot_boxplot(results)
Sự thật cơ bản: Hamiltonian Monte Carlo (HMC)
Chúng tôi sử dụng HMC để tạo ra các mẫu "sự thật cơ bản" từ phần sau của sự thật, để so sánh với kết quả của các bên thay thế.
num_chains = 8
num_leapfrog_steps = 3
step_size = 0.4
num_steps=20000
flat_event_shape = tf.nest.flatten(target_model.event_shape)
enum_components = list(range(len(flat_event_shape)))
bijector = tfb.Restructure(
enum_components,
tf.nest.pack_sequence_as(target_model.event_shape, enum_components))(
target_model.experimental_default_event_space_bijector())
current_state = bijector(
tf.nest.map_structure(
lambda e: tf.zeros([num_chains] + list(e), dtype=tf.float32),
target_model.event_shape))
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_model.unnormalized_log_prob,
num_leapfrog_steps=num_leapfrog_steps,
step_size=[tf.fill(s.shape, step_size) for s in current_state])
hmc = tfp.mcmc.TransformedTransitionKernel(
hmc, bijector)
hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
hmc,
num_adaptation_steps=int(num_steps // 2 * 0.8),
target_accept_prob=0.9)
chain, is_accepted = tf.function(
lambda current_state: tfp.mcmc.sample_chain(
current_state=current_state,
kernel=hmc,
num_results=num_steps // 2,
num_burnin_steps=num_steps // 2,
trace_fn=lambda _, pkr:
(pkr.inner_results.inner_results.is_accepted),
),
autograph=False,
jit_compile=True)(current_state)
accept_rate = tf.reduce_mean(tf.cast(is_accepted, tf.float32))
ess = tf.nest.map_structure(
lambda c: tfp.mcmc.effective_sample_size(
c,
cross_chain_dims=1,
filter_beyond_positive_pairs=True),
chain)
r_hat = tf.nest.map_structure(tfp.mcmc.potential_scale_reduction, chain)
hmc_samples = pack_samples(
tf.nest.pack_sequence_as(target_model.event_shape, chain))
print('Acceptance rate is {}'.format(accept_rate))
Acceptance rate is 0.9008625149726868
Lập đồ thị dấu vết mẫu để kiểm tra sự tỉnh táo kết quả HMC.
def plot_traces(var_name, samples):
fig, axes = plt.subplots(1, 2, figsize=(14, 1.5), sharex='col', sharey='col')
for chain in range(num_chains):
s = samples.numpy()[:, chain]
axes[0].plot(s, alpha=0.7)
sns.kdeplot(s, ax=axes[1], shade=False)
axes[0].title.set_text("'{}' trace".format(var_name))
axes[1].title.set_text("'{}' distribution".format(var_name))
axes[0].set_xlabel('Iteration')
warnings.filterwarnings('ignore')
for var, var_samples in hmc_samples.items():
plot_traces(var, var_samples)




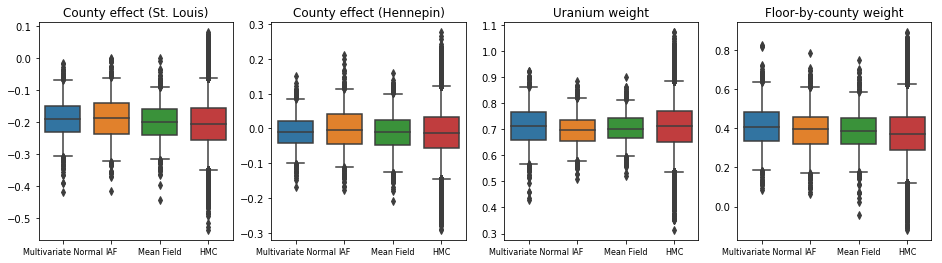
Cả ba cơ quan hậu kiểm thay thế đều tạo ra những khoảng đáng tin cậy tương tự về mặt trực quan với các mẫu HMC, mặc dù đôi khi bị phân tán kém do ảnh hưởng của sự mất mát ELBO, như phổ biến trong VI.
results['HMC'] = hmc_samples
plot_boxplot(results)
Kết quả bổ sung
Các chức năng vẽ đồ thị
plt.rcParams.update({'axes.titlesize': 'medium', 'xtick.labelsize': 'medium'})
def plot_loss_and_elbo():
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].scatter([0, 1, 2],
[mvn_final_elbo.numpy(),
iaf_final_elbo.numpy(),
mean_field_final_elbo.numpy()])
axes[0].set_xticks(ticks=[0, 1, 2])
axes[0].set_xticklabels(labels=[
'Multivariate Normal', 'IAF', 'Mean Field'])
axes[0].title.set_text('Evidence Lower Bound (ELBO)')
axes[1].plot(mvn_loss, label='Multivariate Normal')
axes[1].plot(iaf_loss, label='IAF')
axes[1].plot(mean_field_loss, label='Mean Field')
axes[1].set_ylim([1000, 4000])
axes[1].set_xlabel('Training step')
axes[1].set_ylabel('Loss (negative ELBO)')
axes[1].title.set_text('Loss')
plt.legend()
plt.show()
plt.rcParams.update({'axes.titlesize': 'medium', 'xtick.labelsize': 'small'})
def plot_kdes(num_chains=8):
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
k = list(results.values())[0].keys()
plot_results = {
v: {p: results[p][v] for p in results} for v in k}
for i, (var, var_results) in enumerate(plot_results.items()):
ax = axes[i % 2, i // 2]
for posterior, posterior_results in var_results.items():
if posterior == 'HMC':
label = posterior
for chain in range(num_chains):
sns.kdeplot(
posterior_results[:, chain],
ax=ax, shade=False, color='k', linestyle=':', label=label)
label=None
else:
sns.kdeplot(
posterior_results, ax=ax, shade=False, label=posterior)
ax.title.set_text('{}'.format(var))
ax.legend()
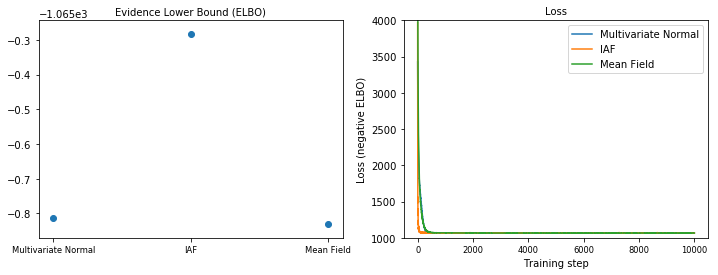
Giới hạn dưới bằng chứng (ELBO)
IAF, cho đến nay là cơ quan thay thế lớn nhất và linh hoạt nhất, hội tụ với Giới hạn dưới bằng chứng cao nhất (ELBO).
plot_loss_and_elbo()
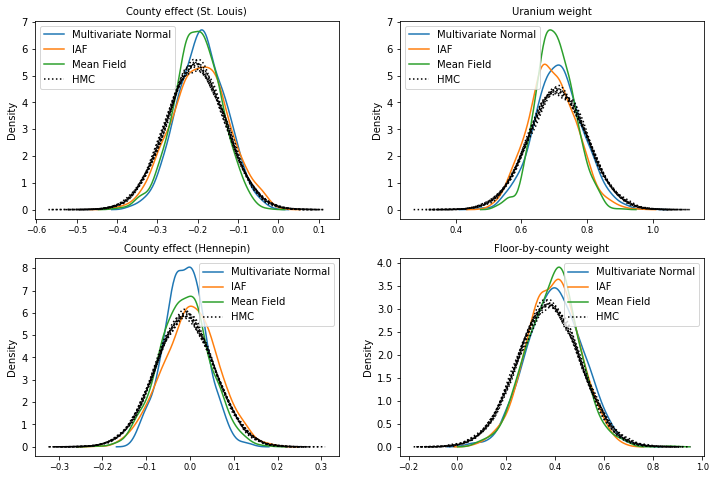
Mẫu sau
Các mẫu từ mỗi phần sau thay thế, được so sánh với các mẫu chân thực trên mặt đất HMC (một hình dung khác về các mẫu được hiển thị trong các ô hộp).
plot_kdes()
Sự kết luận
Trong Colab này, chúng tôi đã xây dựng các mã hậu đại diện VI bằng cách sử dụng các phân phối chung và bộ bijector nhiều phần, và điều chỉnh chúng để ước tính các khoảng đáng tin cậy cho các trọng số trong một mô hình hồi quy trên tập dữ liệu radon. Đối với mô hình đơn giản này, hậu quả đại diện biểu cảm hơn được thực hiện tương tự như hậu quả đại diện trường trung bình. Tuy nhiên, các công cụ mà chúng tôi đã trình bày có thể được sử dụng để xây dựng một loạt các công cụ đại diện thay thế linh hoạt phù hợp với các mô hình phức tạp hơn.
