 TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
Varyasyon Çıkarımı (VI), bir optimizasyon problemi olarak yaklaşık Bayes çıkarımı yapar ve gerçek sonsal ile KL sapmasını en aza indiren bir 'vekil' sonsal dağılım arar. Gradyan tabanlı VI, genellikle MCMC yöntemlerinden daha hızlıdır, model parametrelerinin optimizasyonu ile doğal olarak oluşur ve model karşılaştırması, yakınsama teşhisi ve birleştirilebilir çıkarım için doğrudan kullanılabilen model kanıtı üzerinde bir alt sınır sağlar.
TensorFlow Probability, TFP yığınına doğal olarak uyan hızlı, esnek ve ölçeklenebilir VI araçları sunar. Bu araçlar, doğrusal dönüşümler veya normalleştirme akışları tarafından indüklenen kovaryans yapılarına sahip vekil arka planların oluşturulmasını sağlar.
VI Bayes tahmin etmek için kullanılabilir güvenilir aralıklara ilgi sonucu üzerinde çeşitli tedavilerin veya gözlenen özelliklerin etkilerini tahmin etmek için bir regresyon modelinin parametreleri için. Güvenilir aralıklar, gözlemlenen verilere koşullandırılan ve parametrenin önceki dağılımına ilişkin bir varsayım verilen parametrenin sonsal dağılımına göre, gözlemlenmeyen bir parametrenin değerlerini belirli bir olasılıkla sınırlar.
(Kullanarak bu CoLab, biz evlerde ölçülen radon düzeyleri için regresyon modelinin doğrusal bir Bayesian parametreleri için inandırıcı aralıklarını elde etmek VI nasıl kullanıldığını göstermektedir . (2007) Radon veri kümesi Gelman ve arkadaşları ; bkz benzer örnekler Stan). Biz TFP nasıl göstermek JointDistribution ler ile birleştirmek bijectors sürüme ve anlamlı vekil posteriors iki tür sığdırmak:
- bir blok matris tarafından dönüştürülmüş standart bir Normal dağılım. Matris, posteriorun bazı bileşenleri arasındaki bağımsızlığı ve diğerleri arasındaki bağımlılığı yansıtabilir, bir ortalama alan veya tam kovaryans posterior varsayımını gevşetebilir.
- Daha karmaşık, daha yüksek kapasiteli kendiliğinden gerileyen akış ters .
Vekil posteriorlar eğitilir ve bir ortalama alan vekil posterior taban çizgisinden elde edilen sonuçlarla ve Hamiltonian Monte Carlo'dan yer gerçeği örnekleriyle karşılaştırılır.
Bayes Varyasyon Çıkarımına Genel Bakış
Aşağıdaki üretici sürecini, varsayalım \(\theta\) , rasgele parametreleri temsil \(\omega\) deterministik parametreleri temsil eder ve \(x_i\) özelliklerdir ve \(y_i\) için hedef değerlerdir \(i=1,\ldots,n\) veri noktaları gözlenen: \ {hizalama başlayacak } &\theta \sim r(\Theta) && \text{(Önce)}\ &\text{için } i = 1 \ldots n: \nonumber \ &\quad y_i \sim p(Y_i|x_i, \theta , \ omega) && \ metin {(Olabilirlik)} \ end {hizalama}
VI daha sonra şu şekilde karakterize edilir: $\newcommand{\E}{\operatorname{\mathbb{E} } } \newcommand{\K}{\operatorname{\mathbb{K} } } \newcommand{\defeq}{\overset {\tiny\text{def} }{=} } \DeclareMathOperator*{\argmin}{arg\,min}$
\ log p ({Y_I} _I ^ n | {x_i} _I ^ n \ omega) - {hizalama} başlar \ & \ defeq - \ log \ int \ textrm {d} \ teta \ r (\ teta) \ prod_i^np(y_i|x_i,\theta, \omega) && \text{(Gerçekten sert integral)} \ &= -\log \int \textrm{d}\theta\, q(\theta) \frac{1 }{q(\theta)} r(\theta) \prod_i^np(y_i|x_i,\theta, \omega) && \text{(1 ile çarp)}\ &\le - \int \textrm{d} \ teta \ q (\ teta) \ günlük \ frac {r (\ teta) \ prod_i ^ np (Y_I | x i \ theta \ omega)} {q (\ teta)} && \ metin {(Jensen eşitsizliği )} \ \ & defeq \ e {q (\ Teta)} [- \ log p (Y_I | x_i, \ Teta \ omega)] + '\ K [q (\ Teta) r (\ Teta)] \ ve \ defeq \text{expected negative log likelihood"} + \ metni {kl regularizer"} \ end {hizalama}
(Teknik olarak elimizde varsayıyoruz \(q\) olduğu mutlak sürekli açısından \(r\). Ayrıca bkz, Jensen eşitsizliği .)
Sınır tüm q için geçerli olduğundan, aşağıdakiler için en sıkı olduğu açıktır:
\[q^*,w^* = \argmin_{q \in \mathcal{Q},\omega\in\mathbb{R}^d} \left\{ \sum_i^n\E_{q(\Theta)}\left[ -\log p(y_i|x_i,\Theta, \omega) \right] + \K[q(\Theta), r(\Theta)] \right\}\]
Terminoloji ile ilgili olarak, diyoruz
- \(q^*\) "vekil posterior" ve,
- \(\mathcal{Q}\) "vekil ailesi."
\(\omega^*\) VI kaybında belirleyici parametrelerin en yüksek olabilirlik değerlerini temsil eder. Bkz bu anketi değişimsel çıkarım ilgili daha fazla bilgi için.
Örnek: Radon ölçümlerinde Bayes hiyerarşik doğrusal regresyon
Radon, evlere yerle temas noktalarından giren radyoaktif bir gazdır. Sigara içmeyenlerde akciğer kanserinin birincil nedeni olan bir kanserojendir. Radon seviyeleri haneden haneye büyük farklılıklar gösterir.
EPA, 80.000 evde radon seviyeleri üzerine bir çalışma yaptı. İki önemli öngörücü:
- Ölçümün yapıldığı kat (bodrum katlarında radon daha yüksek)
- İlçe uranyum seviyesi (radon seviyeleri ile pozitif korelasyon)
İlçe göre gruplandırılmış evlerde radon seviyeleri tahmin getirdiği Bayes hiyerarşik modellemede klasik bir sorundur, Gelman ve Tepesi (2006) . Hiyerarşinin evlerin ilçelere göre gruplandırılması olduğu evlerde radon ölçümlerini tahmin etmek için hiyerarşik bir doğrusal model oluşturacağız. Minnesota'daki evlerin radon seviyesi üzerindeki konumun (ilçenin) etkisi için güvenilir aralıklarla ilgileniyoruz. Bu etkiyi izole etmek için zemin ve uranyum seviyesinin etkileri de modele dahil edilmiştir. Ek olarak, ilçe bazında ölçümün yapıldığı ortalama zemine karşılık gelen bağlamsal bir etkiyi dahil edeceğiz, böylece ölçümlerin yapıldığı zeminin ilçeleri arasında farklılıklar varsa, bu ilçe etkisine atfedilmez.
pip3 install -q tf-nightly tfp-nightly
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow as tf
import tensorflow_datasets as tfds
import tensorflow_probability as tfp
import warnings
tfd = tfp.distributions
tfb = tfp.bijectors
plt.rcParams['figure.facecolor'] = '1.'
# Load the Radon dataset from `tensorflow_datasets` and filter to data from
# Minnesota.
dataset = tfds.as_numpy(
tfds.load('radon', split='train').filter(
lambda x: x['features']['state'] == 'MN').batch(10**9))
# Dependent variable: Radon measurements by house.
dataset = next(iter(dataset))
radon_measurement = dataset['activity'].astype(np.float32)
radon_measurement[radon_measurement <= 0.] = 0.1
log_radon = np.log(radon_measurement)
# Measured uranium concentrations in surrounding soil.
uranium_measurement = dataset['features']['Uppm'].astype(np.float32)
log_uranium = np.log(uranium_measurement)
# County indicator.
county_strings = dataset['features']['county'].astype('U13')
unique_counties, county = np.unique(county_strings, return_inverse=True)
county = county.astype(np.int32)
num_counties = unique_counties.size
# Floor on which the measurement was taken.
floor_of_house = dataset['features']['floor'].astype(np.int32)
# Average floor by county (contextual effect).
county_mean_floor = []
for i in range(num_counties):
county_mean_floor.append(floor_of_house[county == i].mean())
county_mean_floor = np.array(county_mean_floor, dtype=log_radon.dtype)
floor_by_county = county_mean_floor[county]
Regresyon modeli aşağıdaki gibi belirlenir:
\(\newcommand{\Normal}{\operatorname{\sf Normal} }\){hizalama} başlar ve \ \ Metin {uranium_weight} \ sim \ Normal (0, 1) \ \ & metni {county_floor_weight} \ sim \ Normal (0, 1) \ \ & metni {için} j = 1 \ ldots \text{num_counties}:\ &\quad \text{county_effect}_j \sim \Normal (0, \sigma_c)\ &\text{için } i = 1\ldots n:\ &\quad \mu_i = ( \ ve \ dört \ dört \ metni {önyargı} \ & \ dört \ dört + \ metni {il etkisi} {\ metni {il} _I} \ & \ dört \ dört + \ metni {log_uranium} _I \ günlerin \ metni {uranium_weight } \ & \ dört \ dört + \ metni {floor_of_house} _I \ günlerin \ metni {floor_weight} \ & \ dört \ dört + \ metni {floor_by il} {\ metni {il} _I} \ günlerin \ metni {county_floor_weight}) \ \ & dört \ metni {log_radon} _I (\ sigma_y \ mu_i) \ ucu {hizalamak} ki burada \ Normal sim \ \(i\) endeksler gözlemleri ve \(\text{county}_i\) il olduğu \(i\)inci gözlemidir alınmış.
Coğrafi çeşitliliği yakalamak için ilçe düzeyinde rastgele bir etki kullanıyoruz. Parametreler uranium_weight ve county_floor_weight olasılıksal modellenmiş ve floor_weight ve sürekli bias deterministik bulunmaktadır. Bu modelleme seçimleri büyük ölçüde keyfidir ve VI'yı olası bir makul karmaşıklık modeli üzerinde göstermek amacıyla yapılmıştır. Radon veri kümesini kullanarak TFV sabit ve rastgele etkileri ile düzeyli modelleme daha kapsamlı bir tartışma için, bkz Düzeyli Modelleme Primer ve Değişimsel Çıkarım kullanarak takılması Genelleştirilmiş Lineer Karışık etkiler Modelleri .
# Create variables for fixed effects.
floor_weight = tf.Variable(0.)
bias = tf.Variable(0.)
# Variables for scale parameters.
log_radon_scale = tfp.util.TransformedVariable(1., tfb.Exp())
county_effect_scale = tfp.util.TransformedVariable(1., tfb.Exp())
# Define the probabilistic graphical model as a JointDistribution.
@tfd.JointDistributionCoroutineAutoBatched
def model():
uranium_weight = yield tfd.Normal(0., scale=1., name='uranium_weight')
county_floor_weight = yield tfd.Normal(
0., scale=1., name='county_floor_weight')
county_effect = yield tfd.Sample(
tfd.Normal(0., scale=county_effect_scale),
sample_shape=[num_counties], name='county_effect')
yield tfd.Normal(
loc=(log_uranium * uranium_weight + floor_of_house* floor_weight
+ floor_by_county * county_floor_weight
+ tf.gather(county_effect, county, axis=-1)
+ bias),
scale=log_radon_scale[..., tf.newaxis],
name='log_radon')
# Pin the observed `log_radon` values to model the un-normalized posterior.
target_model = model.experimental_pin(log_radon=log_radon)
Etkileyici vekil posteriorlar
Daha sonra, iki farklı türde vekil sonda ile VI kullanarak rastgele etkilerin sonsal dağılımlarını tahmin ediyoruz:
- Blok şeklinde bir matris dönüşümü tarafından indüklenen kovaryans yapısı ile kısıtlı bir çok değişkenli Normal dağılım.
- Bir tarafından dönüştürülmüş değişkenli Standart Normal dağılım Ters Autoregressive Akış daha sonra bölünmüş ve arka desteğini eşleşecek şekilde yeniden yapılandırılmış.
Çok değişkenli Normal vekil arka
Bu vekil sondayı oluşturmak için, arka bileşenin bileşenleri arasında korelasyonu indüklemek için eğitilebilir bir doğrusal operatör kullanılır.
# Determine the `event_shape` of the posterior, and calculate the size of each
# `event_shape` component. These determine the sizes of the components of the
# underlying standard Normal distribution, and the dimensions of the blocks in
# the blockwise matrix transformation.
event_shape = target_model.event_shape_tensor()
flat_event_shape = tf.nest.flatten(event_shape)
flat_event_size = tf.nest.map_structure(tf.reduce_prod, flat_event_shape)
# The `event_space_bijector` maps unconstrained values (in R^n) to the support
# of the prior -- we'll need this at the end to constrain Multivariate Normal
# samples to the prior's support.
event_space_bijector = target_model.experimental_default_event_space_bijector()
Bir Construct JointDistribution karşılık gelen önceki bileşenleri tarafından belirlenen boyutlarda vektör değerli standart normal bileşenleri,. Bileşenler, doğrusal operatör tarafından dönüştürülebilmeleri için vektör değerli olmalıdır.
base_standard_dist = tfd.JointDistributionSequential(
[tfd.Sample(tfd.Normal(0., 1.), s) for s in flat_event_size])
Eğitilebilir bir blok şeklinde alt üçgen doğrusal operatör oluşturun. Bir (eğitilebilir) blok şeklinde matris dönüşümü uygulamak ve posteriorun korelasyon yapısını indüklemek için bunu standart Normal dağılıma uygulayacağız.
Sıfır (veya bir blok ise blok şeklinde lineer operatörün içinde, bir trainable dolu matris blok, posterior iki bileşen arasında tam kovaryans temsil None ) bağımsızlığını ifade eder. Köşegen üzerindeki bloklar ya alt üçgen ya da köşegen matrislerdir, böylece tüm blok yapısı bir alt üçgen matrisi temsil eder.
Bu bijektörün taban dağılımına uygulanması, ortalama 0 ve (Cholesky faktörlü) kovaryansı alt üçgen blok matrisine eşit olan çok değişkenli bir Normal dağılımla sonuçlanır.
operators = (
(tf.linalg.LinearOperatorDiag,), # Variance of uranium weight (scalar).
(tf.linalg.LinearOperatorFullMatrix, # Covariance between uranium and floor-by-county weights.
tf.linalg.LinearOperatorDiag), # Variance of floor-by-county weight (scalar).
(None, # Independence between uranium weight and county effects.
None, # Independence between floor-by-county and county effects.
tf.linalg.LinearOperatorDiag) # Independence among the 85 county effects.
)
block_tril_linop = (
tfp.experimental.vi.util.build_trainable_linear_operator_block(
operators, flat_event_size))
scale_bijector = tfb.ScaleMatvecLinearOperatorBlock(block_tril_linop)
Standart Normal dağılım için doğrusal operatörü uyguladıktan sonra, bir çok parçalı uygulamak Shift ortalama sıfırdan farklı değerler almaya izin vermek bijector.
loc_bijector = tfb.JointMap(
tf.nest.map_structure(
lambda s: tfb.Shift(
tf.Variable(tf.random.uniform(
(s,), minval=-2., maxval=2., dtype=tf.float32))),
flat_event_size))
Ölçek ve konum belirleyicileri ile standart Normal dağılımın dönüştürülmesiyle elde edilen elde edilen çok değişkenli Normal dağılım, öncekiyle eşleşecek şekilde yeniden şekillendirilmeli ve yeniden yapılandırılmalı ve son olarak öncekinin desteğiyle sınırlandırılmalıdır.
# Reshape each component to match the prior, using a nested structure of
# `Reshape` bijectors wrapped in `JointMap` to form a multipart bijector.
reshape_bijector = tfb.JointMap(
tf.nest.map_structure(tfb.Reshape, flat_event_shape))
# Restructure the flat list of components to match the prior's structure
unflatten_bijector = tfb.Restructure(
tf.nest.pack_sequence_as(
event_shape, range(len(flat_event_shape))))
Şimdi hepsini bir araya getirin -- eğitilebilir bijektörleri birbirine zincirleyin ve vekil posterior oluşturmak için bunları temel standart Normal dağılıma uygulayın.
surrogate_posterior = tfd.TransformedDistribution(
base_standard_dist,
bijector = tfb.Chain( # Note that the chained bijectors are applied in reverse order
[
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the posterior
reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
loc_bijector, # allow for nonzero mean
scale_bijector # apply the block matrix transformation to the standard Normal distribution
]))
Çok değişkenli Normal vekil posterior eğitin.
optimizer = tf.optimizers.Adam(learning_rate=1e-2)
mvn_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=16,
jit_compile=True)
mvn_samples = surrogate_posterior.sample(1000)
mvn_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*mvn_samples)
- surrogate_posterior.log_prob(mvn_samples))
print('Multivariate Normal surrogate posterior ELBO: {}'.format(mvn_final_elbo))
plt.plot(mvn_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
Multivariate Normal surrogate posterior ELBO: -1065.705322265625
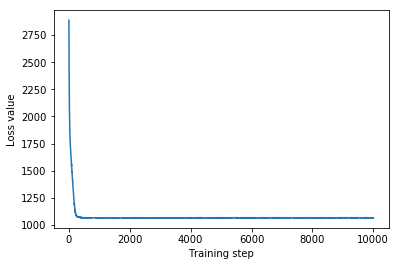
Eğitilmiş vekil sonsal bir TFP dağılımı olduğundan, ondan örnekler alabilir ve parametreler için sonsal güvenilir aralıklar üretmek için bunları işleyebiliriz.
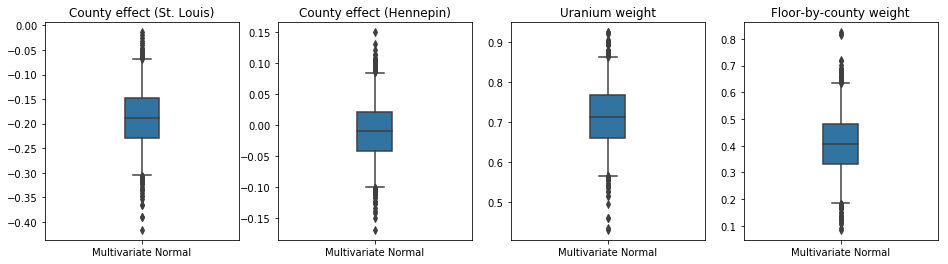
Box-and-bıyık araziler aşağıda% 50 ve% 95 gösteriyor güvenilir aralıklara ilçesinde tarafından ilçe toprak uranyum ölçümlerine büyük iki eyalet ve regresyon ağırlıkları etkisi ve ortalama kat için. İlçe etkileri için arkadaki güvenilir aralıklar, diğer değişkenleri hesaba kattıktan sonra, St. Louis ilçesindeki konumun daha düşük radon seviyeleri ile ilişkili olduğunu ve Hennepin ilçesindeki konumun etkisinin nötre yakın olduğunu göstermektedir.
Regresyon ağırlıklarındaki arka güvenilir aralıklar, daha yüksek toprak uranyum seviyelerinin daha yüksek radon seviyeleri ile ilişkili olduğunu ve ölçümlerin daha yüksek katlarda (muhtemelen evin bodrumu olmadığı için) yapıldığı ilçelerin daha yüksek radon seviyelerine sahip olma eğiliminde olduğunu göstermektedir. zemin özellikleri ve bunların inşa edilen yapıların türü üzerindeki etkileri ile ilgili olabilir.
Zeminin (deterministik) katsayısı negatiftir, bu da beklendiği gibi alt katların daha yüksek radon seviyelerine sahip olduğunu gösterir.
st_louis_co = 69 # Index of St. Louis, the county with the most observations.
hennepin_co = 25 # Index of Hennepin, with the second-most observations.
def pack_samples(samples):
return {'County effect (St. Louis)': samples.county_effect[..., st_louis_co],
'County effect (Hennepin)': samples.county_effect[..., hennepin_co],
'Uranium weight': samples.uranium_weight,
'Floor-by-county weight': samples.county_floor_weight}
def plot_boxplot(posterior_samples):
fig, axes = plt.subplots(1, 4, figsize=(16, 4))
# Invert the results dict for easier plotting.
k = list(posterior_samples.values())[0].keys()
plot_results = {
v: {p: posterior_samples[p][v] for p in posterior_samples} for v in k}
for i, (var, var_results) in enumerate(plot_results.items()):
sns.boxplot(data=list(var_results.values()), ax=axes[i],
width=0.18*len(var_results), whis=(2.5, 97.5))
# axes[i].boxplot(list(var_results.values()), whis=(2.5, 97.5))
axes[i].title.set_text(var)
fs = 10 if len(var_results) < 4 else 8
axes[i].set_xticklabels(list(var_results.keys()), fontsize=fs)
results = {'Multivariate Normal': pack_samples(mvn_samples)}
print('Bias is: {:.2f}'.format(bias.numpy()))
print('Floor fixed effect is: {:.2f}'.format(floor_weight.numpy()))
plot_boxplot(results)
Bias is: 1.40 Floor fixed effect is: -0.72
Ters Otoregresif Akış vekil posterior
Ters Otoregresif Akışlar (IAF'ler), dağılımın bileşenleri arasındaki karmaşık, doğrusal olmayan bağımlılıkları yakalamak için sinir ağlarını kullanan normalleştirici akışlardır. Daha sonra, bu yüksek kapasiteli, daha esnek modelin kısıtlı çok değişkenli Normal'den daha iyi performans gösterip göstermediğini görmek için bir IAF vekili posterior oluşturuyoruz.
# Build a standard Normal with a vector `event_shape`, with length equal to the
# total number of degrees of freedom in the posterior.
base_distribution = tfd.Sample(
tfd.Normal(0., 1.), sample_shape=[tf.reduce_sum(flat_event_size)])
# Apply an IAF to the base distribution.
num_iafs = 2
iaf_bijectors = [
tfb.Invert(tfb.MaskedAutoregressiveFlow(
shift_and_log_scale_fn=tfb.AutoregressiveNetwork(
params=2, hidden_units=[256, 256], activation='relu')))
for _ in range(num_iafs)
]
# Split the base distribution's `event_shape` into components that are equal
# in size to the prior's components.
split = tfb.Split(flat_event_size)
# Chain these bijectors and apply them to the standard Normal base distribution
# to build the surrogate posterior. `event_space_bijector`,
# `unflatten_bijector`, and `reshape_bijector` are the same as in the
# multivariate Normal surrogate posterior.
iaf_surrogate_posterior = tfd.TransformedDistribution(
base_distribution,
bijector=tfb.Chain([
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the prior
reshape_bijector, # reshape the vector-valued components to match the shapes of the prior components
split] + # Split the samples into components of the same size as the prior components
iaf_bijectors # Apply a flow model to the Tensor-valued standard Normal distribution
))
IAF vekili posterior eğitin.
optimizer=tf.optimizers.Adam(learning_rate=1e-2)
iaf_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
iaf_surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=4,
jit_compile=True)
iaf_samples = iaf_surrogate_posterior.sample(1000)
iaf_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*iaf_samples)
- iaf_surrogate_posterior.log_prob(iaf_samples))
print('IAF surrogate posterior ELBO: {}'.format(iaf_final_elbo))
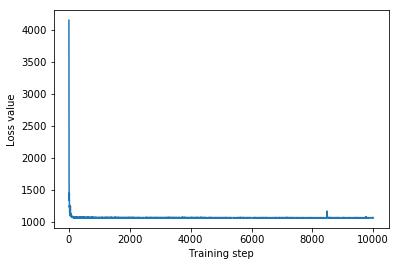
plt.plot(iaf_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
IAF surrogate posterior ELBO: -1065.3663330078125
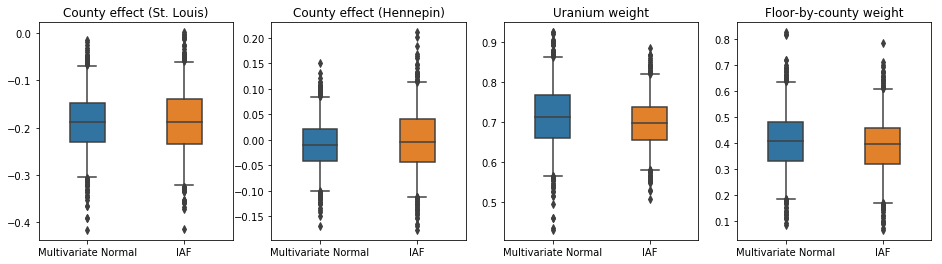
IAF vekili posterior için güvenilir aralıklar, kısıtlı çok değişkenli Normal'inkilere benzer görünmektedir.
results['IAF'] = pack_samples(iaf_samples)
plot_boxplot(results)
Temel: Ortalama alan vekili arka
VI vekil posteriorların genellikle, bir bijektif dönüşümle öncekinin desteğiyle sınırlı, eğitilebilir araçlar ve varyanslarla ortalama alan (bağımsız) Normal dağılımlar olduğu varsayılır. Çok değişkenli Normal vekil posterior ile aynı genel formülü kullanarak, daha anlamlı iki vekil posteriora ek olarak bir ortalama alan vekil posterior tanımlarız.
# A block-diagonal linear operator, in which each block is a diagonal operator,
# transforms the standard Normal base distribution to produce a mean-field
# surrogate posterior.
operators = (tf.linalg.LinearOperatorDiag,
tf.linalg.LinearOperatorDiag,
tf.linalg.LinearOperatorDiag)
block_diag_linop = (
tfp.experimental.vi.util.build_trainable_linear_operator_block(
operators, flat_event_size))
mean_field_scale = tfb.ScaleMatvecLinearOperatorBlock(block_diag_linop)
mean_field_loc = tfb.JointMap(
tf.nest.map_structure(
lambda s: tfb.Shift(
tf.Variable(tf.random.uniform(
(s,), minval=-2., maxval=2., dtype=tf.float32))),
flat_event_size))
mean_field_surrogate_posterior = tfd.TransformedDistribution(
base_standard_dist,
bijector = tfb.Chain( # Note that the chained bijectors are applied in reverse order
[
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the posterior
reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
mean_field_loc, # allow for nonzero mean
mean_field_scale # apply the block matrix transformation to the standard Normal distribution
]))
optimizer=tf.optimizers.Adam(learning_rate=1e-2)
mean_field_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
mean_field_surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=16,
jit_compile=True)
mean_field_samples = mean_field_surrogate_posterior.sample(1000)
mean_field_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*mean_field_samples)
- mean_field_surrogate_posterior.log_prob(mean_field_samples))
print('Mean-field surrogate posterior ELBO: {}'.format(mean_field_final_elbo))
plt.plot(mean_field_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
Mean-field surrogate posterior ELBO: -1065.7652587890625
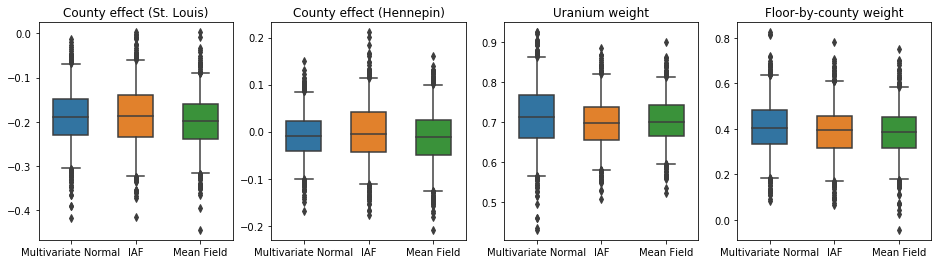
Bu durumda, vekil posterior ortalama alanı, daha anlamlı vekil posteriorlara benzer sonuçlar verir, bu da bu daha basit modelin çıkarım görevi için yeterli olabileceğini gösterir.
results['Mean Field'] = pack_samples(mean_field_samples)
plot_boxplot(results)
Temel gerçek: Hamilton Monte Carlo (HMC)
Vekil posterior sonuçların sonuçlarıyla karşılaştırmak için gerçek posteriordan "temel gerçeği" örnekleri oluşturmak için HMC kullanıyoruz.
num_chains = 8
num_leapfrog_steps = 3
step_size = 0.4
num_steps=20000
flat_event_shape = tf.nest.flatten(target_model.event_shape)
enum_components = list(range(len(flat_event_shape)))
bijector = tfb.Restructure(
enum_components,
tf.nest.pack_sequence_as(target_model.event_shape, enum_components))(
target_model.experimental_default_event_space_bijector())
current_state = bijector(
tf.nest.map_structure(
lambda e: tf.zeros([num_chains] + list(e), dtype=tf.float32),
target_model.event_shape))
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_model.unnormalized_log_prob,
num_leapfrog_steps=num_leapfrog_steps,
step_size=[tf.fill(s.shape, step_size) for s in current_state])
hmc = tfp.mcmc.TransformedTransitionKernel(
hmc, bijector)
hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
hmc,
num_adaptation_steps=int(num_steps // 2 * 0.8),
target_accept_prob=0.9)
chain, is_accepted = tf.function(
lambda current_state: tfp.mcmc.sample_chain(
current_state=current_state,
kernel=hmc,
num_results=num_steps // 2,
num_burnin_steps=num_steps // 2,
trace_fn=lambda _, pkr:
(pkr.inner_results.inner_results.is_accepted),
),
autograph=False,
jit_compile=True)(current_state)
accept_rate = tf.reduce_mean(tf.cast(is_accepted, tf.float32))
ess = tf.nest.map_structure(
lambda c: tfp.mcmc.effective_sample_size(
c,
cross_chain_dims=1,
filter_beyond_positive_pairs=True),
chain)
r_hat = tf.nest.map_structure(tfp.mcmc.potential_scale_reduction, chain)
hmc_samples = pack_samples(
tf.nest.pack_sequence_as(target_model.event_shape, chain))
print('Acceptance rate is {}'.format(accept_rate))
Acceptance rate is 0.9008625149726868
HMC sonuçlarını akıl sağlığı açısından kontrol etmek için örnek izlerini çizin.
def plot_traces(var_name, samples):
fig, axes = plt.subplots(1, 2, figsize=(14, 1.5), sharex='col', sharey='col')
for chain in range(num_chains):
s = samples.numpy()[:, chain]
axes[0].plot(s, alpha=0.7)
sns.kdeplot(s, ax=axes[1], shade=False)
axes[0].title.set_text("'{}' trace".format(var_name))
axes[1].title.set_text("'{}' distribution".format(var_name))
axes[0].set_xlabel('Iteration')
warnings.filterwarnings('ignore')
for var, var_samples in hmc_samples.items():
plot_traces(var, var_samples)




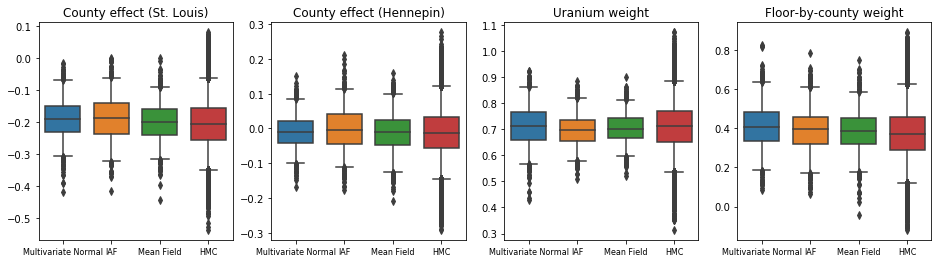
Üç vekil posteriorun tümü, VI'da yaygın olduğu gibi, bazen ELBO kaybının etkisinden dolayı yetersiz dağılmış olsa da, görsel olarak HMC örneklerine benzeyen güvenilir aralıklar üretti.
results['HMC'] = hmc_samples
plot_boxplot(results)
Ek sonuçlar
Çizim fonksiyonları
plt.rcParams.update({'axes.titlesize': 'medium', 'xtick.labelsize': 'medium'})
def plot_loss_and_elbo():
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].scatter([0, 1, 2],
[mvn_final_elbo.numpy(),
iaf_final_elbo.numpy(),
mean_field_final_elbo.numpy()])
axes[0].set_xticks(ticks=[0, 1, 2])
axes[0].set_xticklabels(labels=[
'Multivariate Normal', 'IAF', 'Mean Field'])
axes[0].title.set_text('Evidence Lower Bound (ELBO)')
axes[1].plot(mvn_loss, label='Multivariate Normal')
axes[1].plot(iaf_loss, label='IAF')
axes[1].plot(mean_field_loss, label='Mean Field')
axes[1].set_ylim([1000, 4000])
axes[1].set_xlabel('Training step')
axes[1].set_ylabel('Loss (negative ELBO)')
axes[1].title.set_text('Loss')
plt.legend()
plt.show()
plt.rcParams.update({'axes.titlesize': 'medium', 'xtick.labelsize': 'small'})
def plot_kdes(num_chains=8):
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
k = list(results.values())[0].keys()
plot_results = {
v: {p: results[p][v] for p in results} for v in k}
for i, (var, var_results) in enumerate(plot_results.items()):
ax = axes[i % 2, i // 2]
for posterior, posterior_results in var_results.items():
if posterior == 'HMC':
label = posterior
for chain in range(num_chains):
sns.kdeplot(
posterior_results[:, chain],
ax=ax, shade=False, color='k', linestyle=':', label=label)
label=None
else:
sns.kdeplot(
posterior_results, ax=ax, shade=False, label=posterior)
ax.title.set_text('{}'.format(var))
ax.legend()
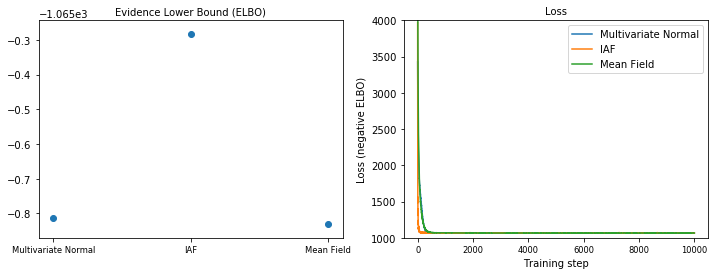
Kanıt Alt Sınırı (ELBO)
Açık farkla en büyük ve en esnek vekil posterior olan IAF, en yüksek Kanıt Alt Sınırına (ELBO) yakınsar.
plot_loss_and_elbo()
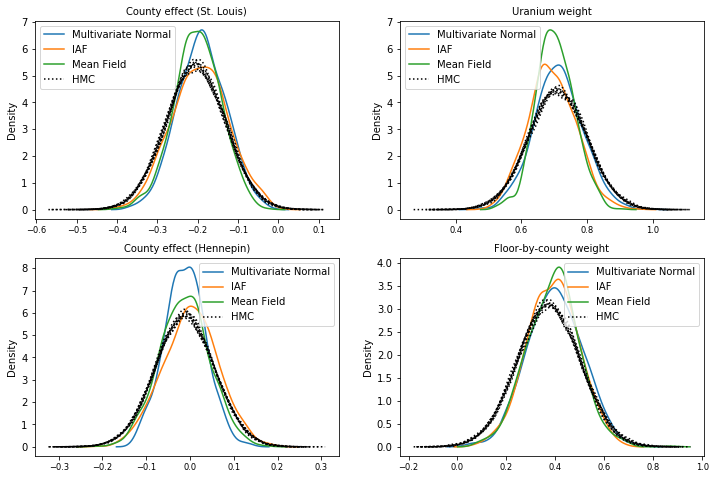
Arka örnekler
Her bir vekil posteriordan alınan örnekler, HMC temel doğruluk örnekleriyle karşılaştırıldığında (kutu grafiklerinde gösterilen örneklerin farklı bir görselleştirmesi).
plot_kdes()
Çözüm
Bu İşbirliğinde, ortak dağılımlar ve çok parçalı bijektörler kullanarak VI vekil posteriorlar oluşturduk ve bunları radon veri setinde bir regresyon modelinde ağırlıklar için güvenilir aralıkları tahmin etmek üzere yerleştirdik. Bu basit model için, daha anlamlı vekil posteriorlar, bir ortalama alan vekil posteriora benzer şekilde gerçekleştirilir. Ancak gösterdiğimiz araçlar, daha karmaşık modeller için uygun çok çeşitli esnek vekil posteriorlar oluşturmak için kullanılabilir.
