 Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Inferência Variacional (VI) lança inferência Bayesiana aproximada como um problema de otimização e busca uma distribuição posterior 'substituta' que minimize a divergência KL com a posterior verdadeira. O VI baseado em gradiente geralmente é mais rápido que os métodos MCMC, compõe naturalmente com a otimização dos parâmetros do modelo e fornece um limite inferior na evidência do modelo que pode ser usado diretamente para comparação de modelos, diagnóstico de convergência e inferência combinável.
O TensorFlow Probability oferece ferramentas para VI rápidos, flexíveis e escaláveis que se encaixam naturalmente na pilha TFP. Essas ferramentas permitem a construção de posteriores substitutos com estruturas de covariância induzidas por transformações lineares ou fluxos normalizadores.
VI pode ser usada para estimar Bayesian intervalos credíveis para os parâmetros de um modelo de regressão para estimar os efeitos de vários tratamentos ou características observadas em um resultado de interesse. Intervalos confiáveis ligam os valores de um parâmetro não observado com certa probabilidade, de acordo com a distribuição posterior do parâmetro condicionada aos dados observados e dada uma suposição sobre a distribuição prévia do parâmetro.
Neste Colab, demonstramos como usar VI para obter intervalos credíveis para parâmetros de um Bayesian lineares modelo de regressão para níveis de radão medidos em casas (usando Gelman et al (2007) Radon dataset. , Ver exemplos semelhantes em Stan). Demonstramos como TFP JointDistribution s combinam com bijectors para construir e ajustar dois tipos de traseiros substitutos expressivos:
- uma distribuição Normal padrão transformada por uma matriz de blocos. A matriz pode refletir independência entre alguns componentes da posterior e dependência entre outras, relaxando a suposição de uma posterior de campo médio ou de covariância total.
- uma mais complexa, de maior capacidade inverso de fluxo de auto-regressivo .
Os posteriores substitutos são treinados e comparados com os resultados de uma linha de base posterior substituta de campo médio, bem como amostras de verdade do hamiltoniano Monte Carlo.
Visão geral da inferência variacional bayesiana
Suponha que temos o seguinte processo generativo, onde \(\theta\) representa parâmetros aleatórios, \(\omega\) representa parâmetros determinísticos e os \(x_i\) são características e as \(y_i\) são valores-alvo para \(i=1,\ldots,n\) observados pontos de dados: \ begin {align } &\theta \sim r(\Theta) && \text{(Antes)}\ &\text{para } i = 1 \ldots n: \nonumber \ &\quad y_i \sim p(Y_i|x_i, \theta , \ omega) && \ text {(Probabilidade)} \ end {align}
VI é então caracterizado por: $\newcommand{\E}{\operatorname{\mathbb{E} } } \newcommand{\K}{\operatorname{\mathbb{K} } } \newcommand{\defeq}{\overset {\tiny\text{def} }{=} } \DeclareMathOperator*{\argmin}{arg\,min}$
\ begin {align} - \ log p ({y_i} _i ^ n | {x_i} _i ^ n, \ omega) & \ defeq - \ log \ int \ textrm {d} \ theta \, r (\ theta) \ prod_i^np(y_i|x_i,\theta, \omega) && \text{(Really hard integral)} \ &= -\log \int \textrm{d}\theta\, q(\theta) \frac{1 }{q(\theta)} r(\theta) \prod_i^np(y_i|x_i,\theta, \omega) && \text{(Multiply by 1)}\ &\le - \int \textrm{d} \ theta \, q (\ theta) \ log \ frac {r (\ theta) \ prod_i ^ np (y_i | x i, \ theta, \ omega)} {q (\ theta)} && \ text {(desigualdade de Jensen )} \ & \ defeq \ e {q (\ Theta)} [- \ log p (y_i | x_i, \ Theta, \ omega)] + \ K [q (\ Theta), r (\ Theta)] \ & \ defeq \text{expected negative log likelihood"} + end \ text {regularizer kl"} \ {align}
(Tecnicamente estamos assumindo \(q\) é absolutamente contínua com respeito a \(r\). Veja também, a desigualdade de Jensen .)
Como o limite vale para todo q, é obviamente mais apertado para:
\[q^*,w^* = \argmin_{q \in \mathcal{Q},\omega\in\mathbb{R}^d} \left\{ \sum_i^n\E_{q(\Theta)}\left[ -\log p(y_i|x_i,\Theta, \omega) \right] + \K[q(\Theta), r(\Theta)] \right\}\]
Quanto à terminologia, chamamos
- \(q^*\) o "posterior substituto", e,
- \(\mathcal{Q}\) a "família substituta."
\(\omega^*\) representa os valores de probabilidade máxima dos parâmetros deterministas sobre a perda VI. Veja este levantamento para mais informações sobre inferência variational.
Exemplo: regressão linear hierárquica bayesiana em medições de radônio
O radônio é um gás radioativo que entra nas residências através de pontos de contato com o solo. É um agente cancerígeno que é a principal causa de câncer de pulmão em não-fumantes. Os níveis de radônio variam muito de casa para casa.
A EPA fez um estudo dos níveis de radônio em 80.000 casas. Dois preditores importantes são:
- Andar em que a medição foi feita (radônio mais alto nos porões)
- Nível de urânio do condado (correlação positiva com os níveis de radônio)
Prevendo os níveis de radão em casas agrupadas por município é um problema clássico na modelagem hierárquica bayesiana, introduzido por Gelman e Hill (2006) . Construiremos um modelo linear hierárquico para prever medidas de radônio em casas, em que a hierarquia é o agrupamento de casas por município. Estamos interessados em intervalos confiáveis para o efeito da localização (condado) no nível de radônio das casas em Minnesota. Para isolar este efeito, os efeitos do piso e do nível de urânio também estão incluídos no modelo. Adicionalmente, incorporaremos um efeito contextual correspondente ao piso médio em que a medição foi feita, por município, de modo que se houver variação entre os municípios do piso em que as medições foram feitas, isso não seja atribuído ao efeito município.
pip3 install -q tf-nightly tfp-nightly
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow as tf
import tensorflow_datasets as tfds
import tensorflow_probability as tfp
import warnings
tfd = tfp.distributions
tfb = tfp.bijectors
plt.rcParams['figure.facecolor'] = '1.'
# Load the Radon dataset from `tensorflow_datasets` and filter to data from
# Minnesota.
dataset = tfds.as_numpy(
tfds.load('radon', split='train').filter(
lambda x: x['features']['state'] == 'MN').batch(10**9))
# Dependent variable: Radon measurements by house.
dataset = next(iter(dataset))
radon_measurement = dataset['activity'].astype(np.float32)
radon_measurement[radon_measurement <= 0.] = 0.1
log_radon = np.log(radon_measurement)
# Measured uranium concentrations in surrounding soil.
uranium_measurement = dataset['features']['Uppm'].astype(np.float32)
log_uranium = np.log(uranium_measurement)
# County indicator.
county_strings = dataset['features']['county'].astype('U13')
unique_counties, county = np.unique(county_strings, return_inverse=True)
county = county.astype(np.int32)
num_counties = unique_counties.size
# Floor on which the measurement was taken.
floor_of_house = dataset['features']['floor'].astype(np.int32)
# Average floor by county (contextual effect).
county_mean_floor = []
for i in range(num_counties):
county_mean_floor.append(floor_of_house[county == i].mean())
county_mean_floor = np.array(county_mean_floor, dtype=log_radon.dtype)
floor_by_county = county_mean_floor[county]
O modelo de regressão é especificado da seguinte forma:
\(\newcommand{\Normal}{\operatorname{\sf Normal} }\)\ begin {align} e \ text {uranium_weight} \ sim \ Normal (0, 1) \ & \ text {county_floor_weight} \ sim \ Normal (0, 1) \ & \ text {for} j = 1 \ ldots \text{num_counties}:\ &\quad \text{county_effect}_j \sim \Normal (0, \sigma_c)\ &\text{for } i = 1\ldots n:\ &\quad \mu_i = ( \ & \ quad \ quad \ text {viés} \ & \ quad \ quad + \ text {efeito condado} {\ text {condado} _i} \ & \ quad \ quad + \ text {log_uranium} _i \ times \ texto {uranium_weight } \ & \ quad \ quad + \ text {floor_of_house} _i \ times \ texto {floor_weight} \ & \ quad \ quad + \ text {floor_by condado} {\ text {condado} _i} \ times \ texto {county_floor_weight}) \ & \ quad \ texto {log_radon} _i \ sim \ normal (\ mu_i, \ sigma_y) \ final {align} em que \(i\) indexa as observações e \(\text{county}_i\) é o concelho no qual a \(i\)th observação estava ocupado.
Usamos um efeito aleatório em nível de condado para capturar a variação geográfica. Os parâmetros uranium_weight e county_floor_weight são modelados probabilisticamente, e floor_weight e a constante de bias são deterministas. Essas escolhas de modelagem são amplamente arbitrárias e são feitas com o objetivo de demonstrar VI em um modelo probabilístico de complexidade razoável. Para uma discussão mais aprofundada de modelagem multinível com efeitos fixos e aleatórios em TFP, usando o conjunto de dados de radão, ver Multilevel Modeling Primer e Fitting lineares generalizados de efeitos mistos Models Usando Variational Inference .
# Create variables for fixed effects.
floor_weight = tf.Variable(0.)
bias = tf.Variable(0.)
# Variables for scale parameters.
log_radon_scale = tfp.util.TransformedVariable(1., tfb.Exp())
county_effect_scale = tfp.util.TransformedVariable(1., tfb.Exp())
# Define the probabilistic graphical model as a JointDistribution.
@tfd.JointDistributionCoroutineAutoBatched
def model():
uranium_weight = yield tfd.Normal(0., scale=1., name='uranium_weight')
county_floor_weight = yield tfd.Normal(
0., scale=1., name='county_floor_weight')
county_effect = yield tfd.Sample(
tfd.Normal(0., scale=county_effect_scale),
sample_shape=[num_counties], name='county_effect')
yield tfd.Normal(
loc=(log_uranium * uranium_weight + floor_of_house* floor_weight
+ floor_by_county * county_floor_weight
+ tf.gather(county_effect, county, axis=-1)
+ bias),
scale=log_radon_scale[..., tf.newaxis],
name='log_radon')
# Pin the observed `log_radon` values to model the un-normalized posterior.
target_model = model.experimental_pin(log_radon=log_radon)
Posteriores substitutos expressivos
Em seguida, estimamos as distribuições posteriores dos efeitos aleatórios usando VI com dois tipos diferentes de posteriores substitutos:
- Uma distribuição Normal multivariada restrita, com estrutura de covariância induzida por uma transformação de matriz em blocos.
- A distribuição normal padrão multivariada transformado por um Autoregressive fluxo inverso , que é então dividido e reestruturado para coincidir com o apoio da posterior.
Multivariado Normal substituto posterior
Para construir este posterior substituto, um operador linear treinável é usado para induzir a correlação entre os componentes do posterior.
# Determine the `event_shape` of the posterior, and calculate the size of each
# `event_shape` component. These determine the sizes of the components of the
# underlying standard Normal distribution, and the dimensions of the blocks in
# the blockwise matrix transformation.
event_shape = target_model.event_shape_tensor()
flat_event_shape = tf.nest.flatten(event_shape)
flat_event_size = tf.nest.map_structure(tf.reduce_prod, flat_event_shape)
# The `event_space_bijector` maps unconstrained values (in R^n) to the support
# of the prior -- we'll need this at the end to constrain Multivariate Normal
# samples to the prior's support.
event_space_bijector = target_model.experimental_default_event_space_bijector()
Construir um JointDistribution com componentes normais padrão vectorial, com tamanhos determinados pelos componentes anteriores correspondentes. Os componentes devem ter valores vetoriais para que possam ser transformados pelo operador linear.
base_standard_dist = tfd.JointDistributionSequential(
[tfd.Sample(tfd.Normal(0., 1.), s) for s in flat_event_size])
Construa um operador linear triangular inferior treinável em blocos. Vamos aplicá-lo à distribuição Normal padrão para implementar uma transformação de matriz em blocos (treinável) e induzir a estrutura de correlação da posterior.
Dentro do operador por blocos linear, um bloco de matriz completa orientáveis representa covariância total entre dois componentes da posterior, enquanto um bloco de zeros (ou None ) expressa independência. Os blocos na diagonal são matrizes triangulares inferiores ou diagonais, de modo que toda a estrutura do bloco representa uma matriz triangular inferior.
A aplicação desse bijetor à distribuição de base resulta em uma distribuição Normal multivariada com média 0 e covariância (fatorada por Cholesky) igual à matriz de bloco triangular inferior.
operators = (
(tf.linalg.LinearOperatorDiag,), # Variance of uranium weight (scalar).
(tf.linalg.LinearOperatorFullMatrix, # Covariance between uranium and floor-by-county weights.
tf.linalg.LinearOperatorDiag), # Variance of floor-by-county weight (scalar).
(None, # Independence between uranium weight and county effects.
None, # Independence between floor-by-county and county effects.
tf.linalg.LinearOperatorDiag) # Independence among the 85 county effects.
)
block_tril_linop = (
tfp.experimental.vi.util.build_trainable_linear_operator_block(
operators, flat_event_size))
scale_bijector = tfb.ScaleMatvecLinearOperatorBlock(block_tril_linop)
Após a aplicação do operador linear para a distribuição normal padrão, aplicar um concatenada Shift bijector para permitir que a média para tomar valores diferentes de zero.
loc_bijector = tfb.JointMap(
tf.nest.map_structure(
lambda s: tfb.Shift(
tf.Variable(tf.random.uniform(
(s,), minval=-2., maxval=2., dtype=tf.float32))),
flat_event_size))
A distribuição Normal multivariada resultante, obtida pela transformação da distribuição Normal padrão com os bijetores de escala e localização, deve ser reformulada e reestruturada para corresponder à anterior e, finalmente, restrita ao suporte da anterior.
# Reshape each component to match the prior, using a nested structure of
# `Reshape` bijectors wrapped in `JointMap` to form a multipart bijector.
reshape_bijector = tfb.JointMap(
tf.nest.map_structure(tfb.Reshape, flat_event_shape))
# Restructure the flat list of components to match the prior's structure
unflatten_bijector = tfb.Restructure(
tf.nest.pack_sequence_as(
event_shape, range(len(flat_event_shape))))
Agora, junte tudo -- encadeie os bijetores treináveis e aplique-os à distribuição Normal padrão básica para construir o posterior substituto.
surrogate_posterior = tfd.TransformedDistribution(
base_standard_dist,
bijector = tfb.Chain( # Note that the chained bijectors are applied in reverse order
[
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the posterior
reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
loc_bijector, # allow for nonzero mean
scale_bijector # apply the block matrix transformation to the standard Normal distribution
]))
Treine o posterior substituto normal multivariado.
optimizer = tf.optimizers.Adam(learning_rate=1e-2)
mvn_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=16,
jit_compile=True)
mvn_samples = surrogate_posterior.sample(1000)
mvn_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*mvn_samples)
- surrogate_posterior.log_prob(mvn_samples))
print('Multivariate Normal surrogate posterior ELBO: {}'.format(mvn_final_elbo))
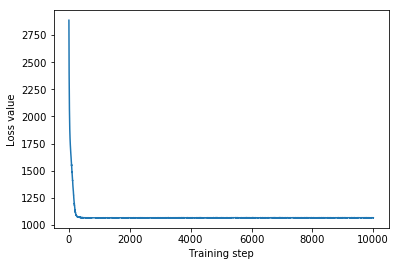
plt.plot(mvn_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
Multivariate Normal surrogate posterior ELBO: -1065.705322265625
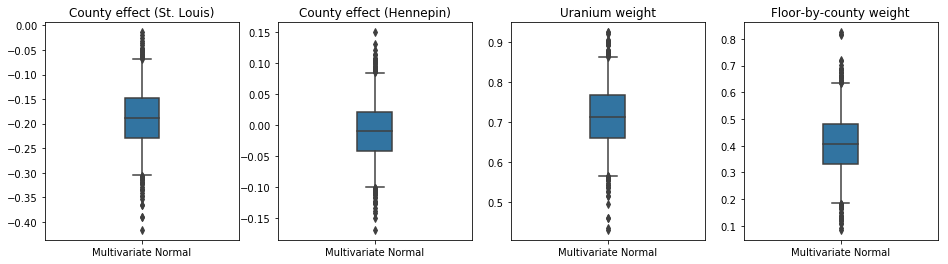
Como a posterior substituta treinada é uma distribuição TFP, podemos coletar amostras dela e processá-las para produzir intervalos críveis posteriores para os parâmetros.
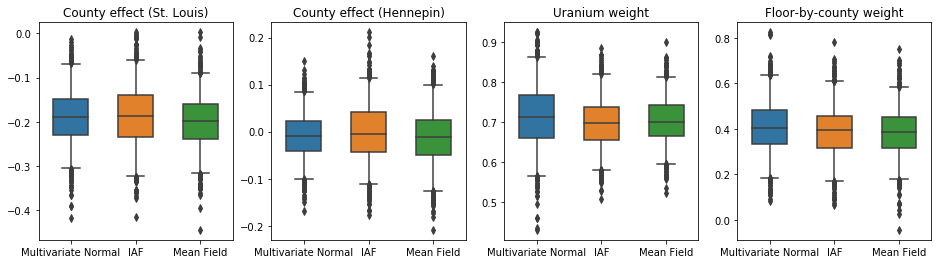
A caixa-e-bigodes abaixo mostram 50% e 95% de intervalo de credibilidade para o efeito condado dos dois maiores municípios e os pesos de regressão em medições de urânio do solo e andar médio por município. Os intervalos de credibilidade posteriores para os efeitos do condado indicam que a localização no condado de St. Louis está associada a níveis mais baixos de radônio, após contabilizar outras variáveis, e que o efeito da localização no condado de Hennepin é quase neutro.
Intervalos de credibilidade posteriores nos pesos de regressão mostram que níveis mais altos de urânio no solo estão associados a níveis mais altos de radônio, e municípios onde as medições foram feitas em andares mais altos (provavelmente porque a casa não tinha um porão) tendem a ter níveis mais altos de radônio, que podem estar relacionadas com as propriedades do solo e o seu efeito no tipo de estruturas construídas.
O coeficiente (determinístico) do piso é negativo, indicando que os pisos inferiores apresentam níveis de radônio mais altos, como esperado.
st_louis_co = 69 # Index of St. Louis, the county with the most observations.
hennepin_co = 25 # Index of Hennepin, with the second-most observations.
def pack_samples(samples):
return {'County effect (St. Louis)': samples.county_effect[..., st_louis_co],
'County effect (Hennepin)': samples.county_effect[..., hennepin_co],
'Uranium weight': samples.uranium_weight,
'Floor-by-county weight': samples.county_floor_weight}
def plot_boxplot(posterior_samples):
fig, axes = plt.subplots(1, 4, figsize=(16, 4))
# Invert the results dict for easier plotting.
k = list(posterior_samples.values())[0].keys()
plot_results = {
v: {p: posterior_samples[p][v] for p in posterior_samples} for v in k}
for i, (var, var_results) in enumerate(plot_results.items()):
sns.boxplot(data=list(var_results.values()), ax=axes[i],
width=0.18*len(var_results), whis=(2.5, 97.5))
# axes[i].boxplot(list(var_results.values()), whis=(2.5, 97.5))
axes[i].title.set_text(var)
fs = 10 if len(var_results) < 4 else 8
axes[i].set_xticklabels(list(var_results.keys()), fontsize=fs)
results = {'Multivariate Normal': pack_samples(mvn_samples)}
print('Bias is: {:.2f}'.format(bias.numpy()))
print('Floor fixed effect is: {:.2f}'.format(floor_weight.numpy()))
plot_boxplot(results)
Bias is: 1.40 Floor fixed effect is: -0.72
Substituto de fluxo autorregressivo inverso posterior
Fluxos Autoregressivos Inversos (IAFs) são fluxos normalizadores que usam redes neurais para capturar dependências complexas e não lineares entre os componentes da distribuição. Em seguida, construímos um posterior substituto do IAF para ver se esse modelo de maior capacidade e mais fiexível supera o normal multivariado restrito.
# Build a standard Normal with a vector `event_shape`, with length equal to the
# total number of degrees of freedom in the posterior.
base_distribution = tfd.Sample(
tfd.Normal(0., 1.), sample_shape=[tf.reduce_sum(flat_event_size)])
# Apply an IAF to the base distribution.
num_iafs = 2
iaf_bijectors = [
tfb.Invert(tfb.MaskedAutoregressiveFlow(
shift_and_log_scale_fn=tfb.AutoregressiveNetwork(
params=2, hidden_units=[256, 256], activation='relu')))
for _ in range(num_iafs)
]
# Split the base distribution's `event_shape` into components that are equal
# in size to the prior's components.
split = tfb.Split(flat_event_size)
# Chain these bijectors and apply them to the standard Normal base distribution
# to build the surrogate posterior. `event_space_bijector`,
# `unflatten_bijector`, and `reshape_bijector` are the same as in the
# multivariate Normal surrogate posterior.
iaf_surrogate_posterior = tfd.TransformedDistribution(
base_distribution,
bijector=tfb.Chain([
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the prior
reshape_bijector, # reshape the vector-valued components to match the shapes of the prior components
split] + # Split the samples into components of the same size as the prior components
iaf_bijectors # Apply a flow model to the Tensor-valued standard Normal distribution
))
Treine o substituto posterior da IAF.
optimizer=tf.optimizers.Adam(learning_rate=1e-2)
iaf_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
iaf_surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=4,
jit_compile=True)
iaf_samples = iaf_surrogate_posterior.sample(1000)
iaf_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*iaf_samples)
- iaf_surrogate_posterior.log_prob(iaf_samples))
print('IAF surrogate posterior ELBO: {}'.format(iaf_final_elbo))
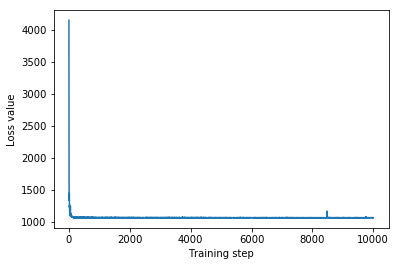
plt.plot(iaf_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
IAF surrogate posterior ELBO: -1065.3663330078125
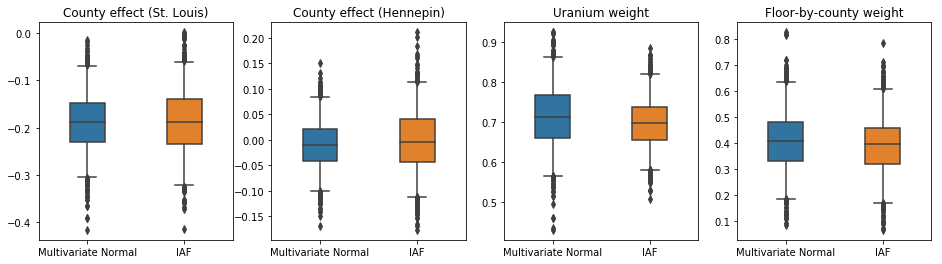
Os intervalos confiáveis para o substituto posterior da IAF parecem semelhantes aos do Normal multivariado restrito.
results['IAF'] = pack_samples(iaf_samples)
plot_boxplot(results)
Linha de base: posterior substituto de campo médio
Os posteriores substitutos do VI são frequentemente assumidos como distribuições normais de campo médio (independentes), com médias e variâncias treináveis, que são restritas ao suporte do anterior com uma transformação bijetiva. Definimos um posterior substituto de campo médio além dos dois posteriores substitutos mais expressivos, usando a mesma fórmula geral do posterior substituto normal multivariado.
# A block-diagonal linear operator, in which each block is a diagonal operator,
# transforms the standard Normal base distribution to produce a mean-field
# surrogate posterior.
operators = (tf.linalg.LinearOperatorDiag,
tf.linalg.LinearOperatorDiag,
tf.linalg.LinearOperatorDiag)
block_diag_linop = (
tfp.experimental.vi.util.build_trainable_linear_operator_block(
operators, flat_event_size))
mean_field_scale = tfb.ScaleMatvecLinearOperatorBlock(block_diag_linop)
mean_field_loc = tfb.JointMap(
tf.nest.map_structure(
lambda s: tfb.Shift(
tf.Variable(tf.random.uniform(
(s,), minval=-2., maxval=2., dtype=tf.float32))),
flat_event_size))
mean_field_surrogate_posterior = tfd.TransformedDistribution(
base_standard_dist,
bijector = tfb.Chain( # Note that the chained bijectors are applied in reverse order
[
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the posterior
reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
mean_field_loc, # allow for nonzero mean
mean_field_scale # apply the block matrix transformation to the standard Normal distribution
]))
optimizer=tf.optimizers.Adam(learning_rate=1e-2)
mean_field_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
mean_field_surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=16,
jit_compile=True)
mean_field_samples = mean_field_surrogate_posterior.sample(1000)
mean_field_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*mean_field_samples)
- mean_field_surrogate_posterior.log_prob(mean_field_samples))
print('Mean-field surrogate posterior ELBO: {}'.format(mean_field_final_elbo))
plt.plot(mean_field_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
Mean-field surrogate posterior ELBO: -1065.7652587890625
Neste caso, o posterior substituto de campo médio fornece resultados semelhantes aos posteriores substitutos mais expressivos, indicando que este modelo mais simples pode ser adequado para a tarefa de inferência.
results['Mean Field'] = pack_samples(mean_field_samples)
plot_boxplot(results)
Verdade do terreno: Hamiltoniano Monte Carlo (HMC)
Usamos o HMC para gerar amostras de "verdade do terreno" do posterior verdadeiro, para comparação com os resultados dos posteriores substitutos.
num_chains = 8
num_leapfrog_steps = 3
step_size = 0.4
num_steps=20000
flat_event_shape = tf.nest.flatten(target_model.event_shape)
enum_components = list(range(len(flat_event_shape)))
bijector = tfb.Restructure(
enum_components,
tf.nest.pack_sequence_as(target_model.event_shape, enum_components))(
target_model.experimental_default_event_space_bijector())
current_state = bijector(
tf.nest.map_structure(
lambda e: tf.zeros([num_chains] + list(e), dtype=tf.float32),
target_model.event_shape))
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_model.unnormalized_log_prob,
num_leapfrog_steps=num_leapfrog_steps,
step_size=[tf.fill(s.shape, step_size) for s in current_state])
hmc = tfp.mcmc.TransformedTransitionKernel(
hmc, bijector)
hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
hmc,
num_adaptation_steps=int(num_steps // 2 * 0.8),
target_accept_prob=0.9)
chain, is_accepted = tf.function(
lambda current_state: tfp.mcmc.sample_chain(
current_state=current_state,
kernel=hmc,
num_results=num_steps // 2,
num_burnin_steps=num_steps // 2,
trace_fn=lambda _, pkr:
(pkr.inner_results.inner_results.is_accepted),
),
autograph=False,
jit_compile=True)(current_state)
accept_rate = tf.reduce_mean(tf.cast(is_accepted, tf.float32))
ess = tf.nest.map_structure(
lambda c: tfp.mcmc.effective_sample_size(
c,
cross_chain_dims=1,
filter_beyond_positive_pairs=True),
chain)
r_hat = tf.nest.map_structure(tfp.mcmc.potential_scale_reduction, chain)
hmc_samples = pack_samples(
tf.nest.pack_sequence_as(target_model.event_shape, chain))
print('Acceptance rate is {}'.format(accept_rate))
Acceptance rate is 0.9008625149726868
Plote traços de amostra para verificar os resultados do HMC.
def plot_traces(var_name, samples):
fig, axes = plt.subplots(1, 2, figsize=(14, 1.5), sharex='col', sharey='col')
for chain in range(num_chains):
s = samples.numpy()[:, chain]
axes[0].plot(s, alpha=0.7)
sns.kdeplot(s, ax=axes[1], shade=False)
axes[0].title.set_text("'{}' trace".format(var_name))
axes[1].title.set_text("'{}' distribution".format(var_name))
axes[0].set_xlabel('Iteration')
warnings.filterwarnings('ignore')
for var, var_samples in hmc_samples.items():
plot_traces(var, var_samples)




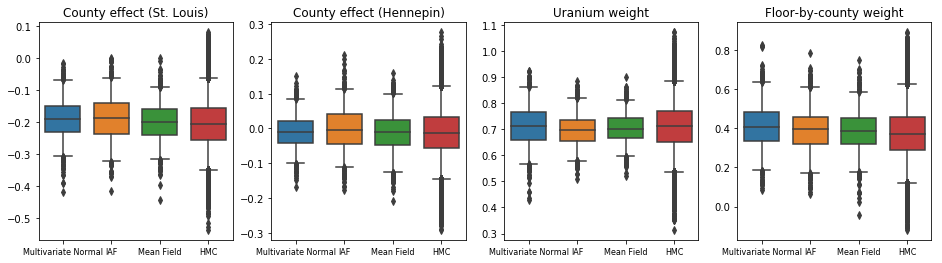
Todos os três posteriores substitutos produziram intervalos críveis que são visualmente semelhantes às amostras de HMC, embora às vezes subdispersos devido ao efeito da perda de ELBO, como é comum em VI.
results['HMC'] = hmc_samples
plot_boxplot(results)
Resultados adicionais
Funções de plotagem
plt.rcParams.update({'axes.titlesize': 'medium', 'xtick.labelsize': 'medium'})
def plot_loss_and_elbo():
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].scatter([0, 1, 2],
[mvn_final_elbo.numpy(),
iaf_final_elbo.numpy(),
mean_field_final_elbo.numpy()])
axes[0].set_xticks(ticks=[0, 1, 2])
axes[0].set_xticklabels(labels=[
'Multivariate Normal', 'IAF', 'Mean Field'])
axes[0].title.set_text('Evidence Lower Bound (ELBO)')
axes[1].plot(mvn_loss, label='Multivariate Normal')
axes[1].plot(iaf_loss, label='IAF')
axes[1].plot(mean_field_loss, label='Mean Field')
axes[1].set_ylim([1000, 4000])
axes[1].set_xlabel('Training step')
axes[1].set_ylabel('Loss (negative ELBO)')
axes[1].title.set_text('Loss')
plt.legend()
plt.show()
plt.rcParams.update({'axes.titlesize': 'medium', 'xtick.labelsize': 'small'})
def plot_kdes(num_chains=8):
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
k = list(results.values())[0].keys()
plot_results = {
v: {p: results[p][v] for p in results} for v in k}
for i, (var, var_results) in enumerate(plot_results.items()):
ax = axes[i % 2, i // 2]
for posterior, posterior_results in var_results.items():
if posterior == 'HMC':
label = posterior
for chain in range(num_chains):
sns.kdeplot(
posterior_results[:, chain],
ax=ax, shade=False, color='k', linestyle=':', label=label)
label=None
else:
sns.kdeplot(
posterior_results, ax=ax, shade=False, label=posterior)
ax.title.set_text('{}'.format(var))
ax.legend()
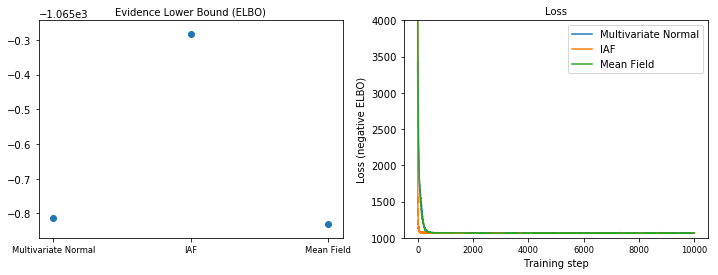
Limite Inferior de Evidência (ELBO)
O IAF, de longe o maior e mais flexível posterior substituto, converge para o limite inferior de evidência (ELBO) mais alto.
plot_loss_and_elbo()
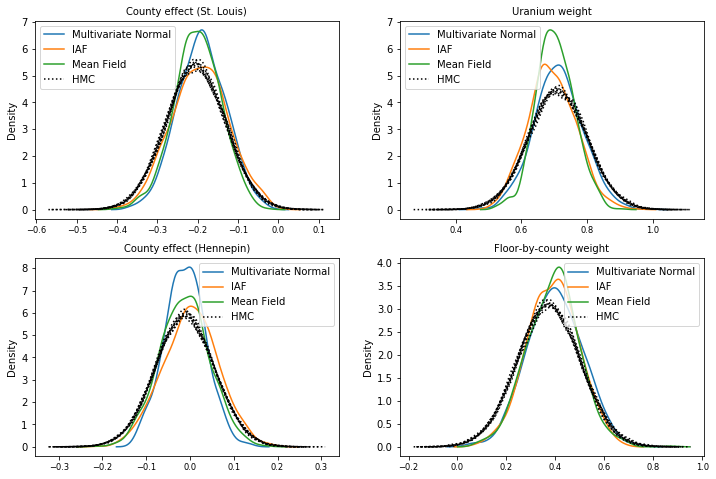
Amostras posteriores
Amostras de cada posterior substituto, comparadas com amostras de verdade do HMC (uma visualização diferente das amostras mostradas nos gráficos de caixa).
plot_kdes()
Conclusão
Neste Colab, construímos posteriores substitutos de VI usando distribuições conjuntas e bijetores multipartes e os ajustamos para estimar intervalos confiáveis para pesos em um modelo de regressão no conjunto de dados de radônio. Para este modelo simples, posteriores substitutos mais expressivos tiveram desempenho semelhante a um posterior substituto de campo médio. As ferramentas que demonstramos, no entanto, podem ser usadas para construir uma ampla gama de posteriores substitutos flexíveis adequados para modelos mais complexos.
