 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza la fonte su GitHub Visualizza la fonte su GitHub |  Scarica taccuino Scarica taccuino |
L'inferenza variazionale (VI) considera l'inferenza bayesiana approssimata come un problema di ottimizzazione e cerca una distribuzione a posteriori "surrogata" che minimizzi la divergenza di KL con il vero posteriore. Il VI basato sul gradiente è spesso più veloce dei metodi MCMC, si compone in modo naturale con l'ottimizzazione dei parametri del modello e fornisce un limite inferiore all'evidenza del modello che può essere utilizzata direttamente per il confronto del modello, la diagnosi della convergenza e l'inferenza componibile.
TensorFlow Probability offre strumenti per VI veloci, flessibili e scalabili che si inseriscono naturalmente nello stack TFP. Questi strumenti consentono la costruzione di posteriori surrogati con strutture di covarianza indotte da trasformazioni lineari o flussi normalizzanti.
VI può essere utilizzato per stimare bayesiani intervallo di credibilità per i parametri di un modello di regressione per stimare gli effetti dei vari trattamenti o caratteristiche osservate su un risultato di interesse. Intervalli credibili vincolano i valori di un parametro non osservato con una certa probabilità, secondo la distribuzione a posteriori del parametro condizionata ai dati osservati e data un'ipotesi sulla distribuzione a priori del parametro.
In questo Colab, dimostriamo come utilizzare VI per ottenere intervalli credibili per i parametri di un bayesiano lineari modello di regressione per i livelli di radon misurati nelle case (utilizzando Gelman et al (2007) Radon dataset. ; Vediamo esempi simili a Stan). Dimostriamo come TFP JointDistribution s combinano con bijectors per costruire e montare due tipi di surrogati posteriori espressive:
- una distribuzione Normale standard trasformata da una matrice a blocchi. La matrice può riflettere l'indipendenza tra alcuni componenti del posteriore e la dipendenza tra gli altri, rilassando l'assunzione di un campo medio o di una covarianza posteriore completa.
- una più complessa e più capiente inversa flusso autoregressivo .
I posteriori surrogati vengono addestrati e confrontati con i risultati di una linea di base posteriore surrogata del campo medio, nonché con campioni di verità a terra da Hamiltonian Monte Carlo.
Panoramica dell'inferenza variazionale bayesiana
Supponiamo di avere il seguente processo generativo, dove \(\theta\) rappresenta parametri casuali, \(\omega\) rappresenta parametri deterministici, e le \(x_i\) sono caratteristiche ei \(y_i\) sono valori obiettivo per \(i=1,\ldots,n\) osservata punti dati: \ begin {align } &\theta \sim r(\Theta) && \text{(Prior)}\ &\text{per } i = 1 \ldots n: \nonumber \ &\quad y_i \sim p(Y_i|x_i, \theta , \ omega) && \ text {(Probabilità)} \ end {align}
VI è quindi caratterizzato da: $\newcommand{\E}{\operatorname{\mathbb{E} } } \newcommand{\K}{\operatorname{\mathbb{K} } } \newcommand{\defeq}{\overset {\tiny\text{def} }{=} } \DeclareMathOperator*{\argmin}{arg\,min}$
\ begin {align} - \ log p ({y_i} _i ^ n | {x_i} _i ^ n, \ omega) e \ defeq - \ log \ int \ textrm {d} \ theta \, r (\ theta) \ prod_i^np(y_i|x_i,\theta, \omega) && \text{(Integrale veramente duro)} \ &= -\log \int \textrm{d}\theta\, q(\theta) \frac{1 }{q(\theta)} r(\theta) \prod_i^np(y_i|x_i,\theta, \omega) && \text{(Moltiplicare per 1)}\ &\le - \int \textrm{d} \ theta \, q (\ theta) \ log \ frac {r (\ theta) \ prod_i ^ np (y_i | x i, \ theta, \ omega)} {q (\ theta)} && \ text {(la disuguaglianza di Jensen )} \ & \ defeq \ e {q (\ theta)} [- \ log p (y_i | x_i, \ Theta, \ omega)] + \ K [q (\ theta), r (\ theta)] \ & \ defeq \text{expected negative log likelihood"} + \ text {regolarizzatore kl"} \ end {align}
(Tecnicamente stiamo assumendo \(q\) è assolutamente continua rispetto alla \(r\). Vedi anche, la disuguaglianza di Jensen .)
Poiché il limite vale per ogni q, è ovviamente più stretto per:
\[q^*,w^* = \argmin_{q \in \mathcal{Q},\omega\in\mathbb{R}^d} \left\{ \sum_i^n\E_{q(\Theta)}\left[ -\log p(y_i|x_i,\Theta, \omega) \right] + \K[q(\Theta), r(\Theta)] \right\}\]
Per quanto riguarda la terminologia, chiamiamo
- \(q^*\) il "posteriore surrogata", e,
- \(\mathcal{Q}\) la "famiglia surrogata."
\(\omega^*\) rappresenta i valori di massima verosimiglianza dei parametri deterministici sulla perdita VI. Vedere questa indagine per ulteriori informazioni sulla deduzione variazionale.
Esempio: regressione lineare gerarchica bayesiana sulle misurazioni del Radon
Il radon è un gas radioattivo che entra nelle case attraverso i punti di contatto con il suolo. È un cancerogeno che è la causa principale del cancro ai polmoni nei non fumatori. I livelli di radon variano notevolmente da famiglia a famiglia.
L'EPA ha condotto uno studio sui livelli di radon in 80.000 case. Due importanti predittori sono:
- Piano su cui è stata effettuata la misurazione (radon più alto negli scantinati)
- Livello di uranio della contea (correlazione positiva con i livelli di radon)
Predire i livelli di radon nelle case raggruppate per contea è un problema classico in bayesiana modellazione gerarchica, introdotto da Gelman e Hill (2006) . Costruiremo un modello lineare gerarchico per prevedere le misurazioni del radon nelle case, in cui la gerarchia è il raggruppamento delle case per contea. Siamo interessati a intervalli credibili per l'effetto della posizione (contea) sul livello di radon delle case in Minnesota. Per isolare questo effetto, nel modello sono inclusi anche gli effetti del livello del pavimento e dell'uranio. Inoltre, incorporeremo un effetto contestuale corrispondente al piano medio su cui è stata effettuata la misurazione, per contea, in modo che se c'è una variazione tra le contee del piano su cui sono state effettuate le misurazioni, ciò non è attribuito all'effetto contea.
pip3 install -q tf-nightly tfp-nightly
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow as tf
import tensorflow_datasets as tfds
import tensorflow_probability as tfp
import warnings
tfd = tfp.distributions
tfb = tfp.bijectors
plt.rcParams['figure.facecolor'] = '1.'
# Load the Radon dataset from `tensorflow_datasets` and filter to data from
# Minnesota.
dataset = tfds.as_numpy(
tfds.load('radon', split='train').filter(
lambda x: x['features']['state'] == 'MN').batch(10**9))
# Dependent variable: Radon measurements by house.
dataset = next(iter(dataset))
radon_measurement = dataset['activity'].astype(np.float32)
radon_measurement[radon_measurement <= 0.] = 0.1
log_radon = np.log(radon_measurement)
# Measured uranium concentrations in surrounding soil.
uranium_measurement = dataset['features']['Uppm'].astype(np.float32)
log_uranium = np.log(uranium_measurement)
# County indicator.
county_strings = dataset['features']['county'].astype('U13')
unique_counties, county = np.unique(county_strings, return_inverse=True)
county = county.astype(np.int32)
num_counties = unique_counties.size
# Floor on which the measurement was taken.
floor_of_house = dataset['features']['floor'].astype(np.int32)
# Average floor by county (contextual effect).
county_mean_floor = []
for i in range(num_counties):
county_mean_floor.append(floor_of_house[county == i].mean())
county_mean_floor = np.array(county_mean_floor, dtype=log_radon.dtype)
floor_by_county = county_mean_floor[county]
Il modello di regressione è specificato come segue:
\(\newcommand{\Normal}{\operatorname{\sf Normal} }\)\ begin {align} e \ text {uranium_weight} \ sim \ Normal (0, 1) \ & \ text {county_floor_weight} \ sim \ Normal (0, 1) \ & \ text {for} j = 1 \ ldots \text{num_counties}:\ &\quad \text{county_effect}_j \sim \Normal (0, \sigma_c)\ &\text{for } i = 1\ldots n:\ &\quad \mu_i = ( \ & \ quad \ quad \ text {pregiudizi} \ & \ quad \ quad + \ text {effetto contea} {\ text {county} _i} \ & \ quad \ quad + \ text {log_uranium} _I \ times \ text {uranium_weight } \ & \ quad \ quad + \ text {floor_of_house} _I \ times \ text {floor_weight} \ & \ quad \ quad + \ text {floor_by contea} {\ text {county} _i} \ times \ text {county_floor_weight}) \ & \ quad \ text {log_radon} _I \ sim \ Normal (\ mu_i, \ sigma_y) \ end {align} in cui \(i\) indici delle osservazioni e \(\text{county}_i\) è la contea in cui la \(i\)esima osservazione è stata prese.
Usiamo un effetto casuale a livello di contea per catturare la variazione geografica. I parametri uranium_weight e county_floor_weight sono modellati probabilistica, e floor_weight e la costante bias sono deterministici. Queste scelte di modellazione sono in gran parte arbitrarie e sono fatte allo scopo di dimostrare VI su un modello probabilistico di ragionevole complessità. Per una discussione più approfondita di modellazione multilivello con effetti fissi e casuali in TFP, utilizzando il set di dati di radon, vedere Multilevel Modeling Primer e di montaggio lineari generalizzati con effetti misti di modelli utilizzando variazionale Inference .
# Create variables for fixed effects.
floor_weight = tf.Variable(0.)
bias = tf.Variable(0.)
# Variables for scale parameters.
log_radon_scale = tfp.util.TransformedVariable(1., tfb.Exp())
county_effect_scale = tfp.util.TransformedVariable(1., tfb.Exp())
# Define the probabilistic graphical model as a JointDistribution.
@tfd.JointDistributionCoroutineAutoBatched
def model():
uranium_weight = yield tfd.Normal(0., scale=1., name='uranium_weight')
county_floor_weight = yield tfd.Normal(
0., scale=1., name='county_floor_weight')
county_effect = yield tfd.Sample(
tfd.Normal(0., scale=county_effect_scale),
sample_shape=[num_counties], name='county_effect')
yield tfd.Normal(
loc=(log_uranium * uranium_weight + floor_of_house* floor_weight
+ floor_by_county * county_floor_weight
+ tf.gather(county_effect, county, axis=-1)
+ bias),
scale=log_radon_scale[..., tf.newaxis],
name='log_radon')
# Pin the observed `log_radon` values to model the un-normalized posterior.
target_model = model.experimental_pin(log_radon=log_radon)
Posteriori surrogati espressivi
Successivamente stimiamo le distribuzioni a posteriori degli effetti casuali utilizzando VI con due diversi tipi di posteriori surrogati:
- Una distribuzione Normale multivariata vincolata, con struttura di covarianza indotta da una trasformazione di matrice a blocchi.
- Una distribuzione multivariata normale standard addestrato da un Autoregressive flusso inverso , che viene poi diviso e ristrutturato per abbinare il supporto del posteriore.
Multivariato Normale surrogato posteriore
Per costruire questo surrogato posteriore, viene utilizzato un operatore lineare addestrabile per indurre la correlazione tra i componenti del posteriore.
# Determine the `event_shape` of the posterior, and calculate the size of each
# `event_shape` component. These determine the sizes of the components of the
# underlying standard Normal distribution, and the dimensions of the blocks in
# the blockwise matrix transformation.
event_shape = target_model.event_shape_tensor()
flat_event_shape = tf.nest.flatten(event_shape)
flat_event_size = tf.nest.map_structure(tf.reduce_prod, flat_event_shape)
# The `event_space_bijector` maps unconstrained values (in R^n) to the support
# of the prior -- we'll need this at the end to constrain Multivariate Normal
# samples to the prior's support.
event_space_bijector = target_model.experimental_default_event_space_bijector()
Costruire una JointDistribution con componenti standard normale valori vettoriali, con dimensioni determinate dai corrispondenti componenti precedenti. I componenti devono essere valutati in vettore in modo che possano essere trasformati dall'operatore lineare.
base_standard_dist = tfd.JointDistributionSequential(
[tfd.Sample(tfd.Normal(0., 1.), s) for s in flat_event_size])
Costruisci un operatore lineare triangolare inferiore a blocchi addestrabile. Lo applicheremo alla distribuzione normale standard per implementare una trasformazione di matrice a blocchi (addestrabile) e indurre la struttura di correlazione del posteriore.
Entro l'operatore a blocchi lineare, un blocco pieno matrice addestrabili rappresenta completo covarianza tra due componenti del posteriori, mentre un blocco di zeri (o None ) esprime indipendenza. I blocchi sulla diagonale sono matrici triangolari inferiori o diagonali, in modo che l'intera struttura del blocco rappresenti una matrice triangolare inferiore.
Applicando questo biiettore alla distribuzione di base si ottiene una distribuzione Normale multivariata con media 0 e covarianza (fattore di Cholesky) uguale alla matrice del blocco triangolare inferiore.
operators = (
(tf.linalg.LinearOperatorDiag,), # Variance of uranium weight (scalar).
(tf.linalg.LinearOperatorFullMatrix, # Covariance between uranium and floor-by-county weights.
tf.linalg.LinearOperatorDiag), # Variance of floor-by-county weight (scalar).
(None, # Independence between uranium weight and county effects.
None, # Independence between floor-by-county and county effects.
tf.linalg.LinearOperatorDiag) # Independence among the 85 county effects.
)
block_tril_linop = (
tfp.experimental.vi.util.build_trainable_linear_operator_block(
operators, flat_event_size))
scale_bijector = tfb.ScaleMatvecLinearOperatorBlock(block_tril_linop)
Dopo aver applicato l'operatore lineare alla distribuzione normale standard, applicare un multipart Shift bijector per consentire al mezzo per prendere valori diversi da zero.
loc_bijector = tfb.JointMap(
tf.nest.map_structure(
lambda s: tfb.Shift(
tf.Variable(tf.random.uniform(
(s,), minval=-2., maxval=2., dtype=tf.float32))),
flat_event_size))
La distribuzione Normale multivariata risultante, ottenuta trasformando la distribuzione Normale standard con i biettori di scala e posizione, deve essere rimodellata e ristrutturata per adeguarla al priore, ed infine vincolata al supporto del priore.
# Reshape each component to match the prior, using a nested structure of
# `Reshape` bijectors wrapped in `JointMap` to form a multipart bijector.
reshape_bijector = tfb.JointMap(
tf.nest.map_structure(tfb.Reshape, flat_event_shape))
# Restructure the flat list of components to match the prior's structure
unflatten_bijector = tfb.Restructure(
tf.nest.pack_sequence_as(
event_shape, range(len(flat_event_shape))))
Ora, metti tutto insieme: concatena insieme i biiettori addestrabili e applicali alla distribuzione normale standard di base per costruire il surrogato posteriore.
surrogate_posterior = tfd.TransformedDistribution(
base_standard_dist,
bijector = tfb.Chain( # Note that the chained bijectors are applied in reverse order
[
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the posterior
reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
loc_bijector, # allow for nonzero mean
scale_bijector # apply the block matrix transformation to the standard Normal distribution
]))
Allena il surrogato normale multivariato posteriore.
optimizer = tf.optimizers.Adam(learning_rate=1e-2)
mvn_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=16,
jit_compile=True)
mvn_samples = surrogate_posterior.sample(1000)
mvn_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*mvn_samples)
- surrogate_posterior.log_prob(mvn_samples))
print('Multivariate Normal surrogate posterior ELBO: {}'.format(mvn_final_elbo))
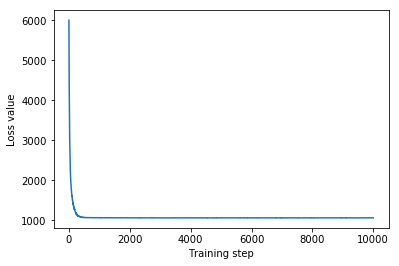
plt.plot(mvn_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
Multivariate Normal surrogate posterior ELBO: -1065.705322265625
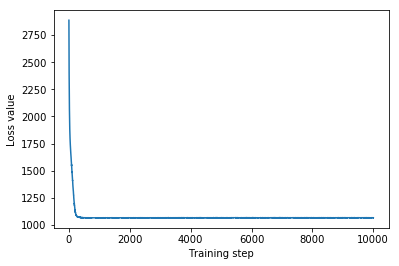
Poiché il surrogato posteriore addestrato è una distribuzione TFP, possiamo prelevarne campioni ed elaborarli per produrre intervalli credibili posteriori per i parametri.
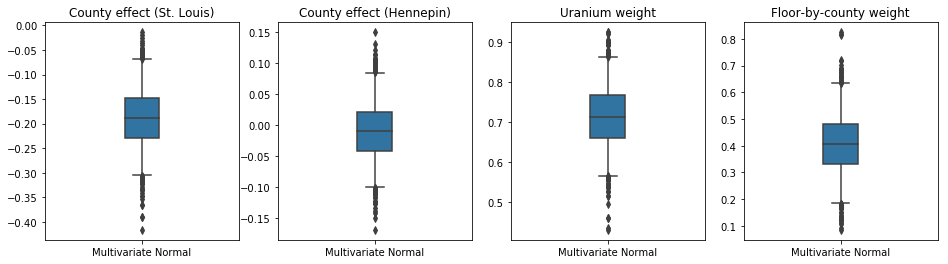
I box-and-baffi trame che seguono mostrano il 50% e il 95% intervallo di credibilità per l'effetto della contea delle due più grandi contee e dei pesi di regressione su misurazioni di uranio suolo e piano media per contea. Gli intervalli di credibilità posteriori per gli effetti della contea indicano che la posizione nella contea di St. Louis è associata a livelli di radon più bassi, dopo aver tenuto conto di altre variabili, e che l'effetto della posizione nella contea di Hennepin è quasi neutrale.
Intervalli credibili posteriori sui pesi di regressione mostrano che livelli più elevati di uranio del suolo sono associati a livelli più elevati di radon e le contee in cui sono state effettuate misurazioni ai piani più alti (probabilmente perché la casa non aveva un seminterrato) tendono ad avere livelli più elevati di radon, che potrebbero riguardare le proprietà del suolo e il loro effetto sul tipo di strutture costruite.
Il coefficiente (deterministico) del pavimento è negativo, indicando che i piani inferiori hanno livelli di radon più elevati, come previsto.
st_louis_co = 69 # Index of St. Louis, the county with the most observations.
hennepin_co = 25 # Index of Hennepin, with the second-most observations.
def pack_samples(samples):
return {'County effect (St. Louis)': samples.county_effect[..., st_louis_co],
'County effect (Hennepin)': samples.county_effect[..., hennepin_co],
'Uranium weight': samples.uranium_weight,
'Floor-by-county weight': samples.county_floor_weight}
def plot_boxplot(posterior_samples):
fig, axes = plt.subplots(1, 4, figsize=(16, 4))
# Invert the results dict for easier plotting.
k = list(posterior_samples.values())[0].keys()
plot_results = {
v: {p: posterior_samples[p][v] for p in posterior_samples} for v in k}
for i, (var, var_results) in enumerate(plot_results.items()):
sns.boxplot(data=list(var_results.values()), ax=axes[i],
width=0.18*len(var_results), whis=(2.5, 97.5))
# axes[i].boxplot(list(var_results.values()), whis=(2.5, 97.5))
axes[i].title.set_text(var)
fs = 10 if len(var_results) < 4 else 8
axes[i].set_xticklabels(list(var_results.keys()), fontsize=fs)
results = {'Multivariate Normal': pack_samples(mvn_samples)}
print('Bias is: {:.2f}'.format(bias.numpy()))
print('Floor fixed effect is: {:.2f}'.format(floor_weight.numpy()))
plot_boxplot(results)
Bias is: 1.40 Floor fixed effect is: -0.72
Surrogato di flusso autoregressivo inverso posteriore
I flussi autoregressivi inversi (IAF) sono flussi di normalizzazione che utilizzano reti neurali per acquisire dipendenze complesse e non lineari tra i componenti della distribuzione. Successivamente costruiamo un surrogato posteriore IAF per vedere se questo modello più flessibile e con capacità più elevata supera il normale multivariato vincolato.
# Build a standard Normal with a vector `event_shape`, with length equal to the
# total number of degrees of freedom in the posterior.
base_distribution = tfd.Sample(
tfd.Normal(0., 1.), sample_shape=[tf.reduce_sum(flat_event_size)])
# Apply an IAF to the base distribution.
num_iafs = 2
iaf_bijectors = [
tfb.Invert(tfb.MaskedAutoregressiveFlow(
shift_and_log_scale_fn=tfb.AutoregressiveNetwork(
params=2, hidden_units=[256, 256], activation='relu')))
for _ in range(num_iafs)
]
# Split the base distribution's `event_shape` into components that are equal
# in size to the prior's components.
split = tfb.Split(flat_event_size)
# Chain these bijectors and apply them to the standard Normal base distribution
# to build the surrogate posterior. `event_space_bijector`,
# `unflatten_bijector`, and `reshape_bijector` are the same as in the
# multivariate Normal surrogate posterior.
iaf_surrogate_posterior = tfd.TransformedDistribution(
base_distribution,
bijector=tfb.Chain([
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the prior
reshape_bijector, # reshape the vector-valued components to match the shapes of the prior components
split] + # Split the samples into components of the same size as the prior components
iaf_bijectors # Apply a flow model to the Tensor-valued standard Normal distribution
))
Addestrare il surrogato posteriore dell'IAF.
optimizer=tf.optimizers.Adam(learning_rate=1e-2)
iaf_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
iaf_surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=4,
jit_compile=True)
iaf_samples = iaf_surrogate_posterior.sample(1000)
iaf_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*iaf_samples)
- iaf_surrogate_posterior.log_prob(iaf_samples))
print('IAF surrogate posterior ELBO: {}'.format(iaf_final_elbo))
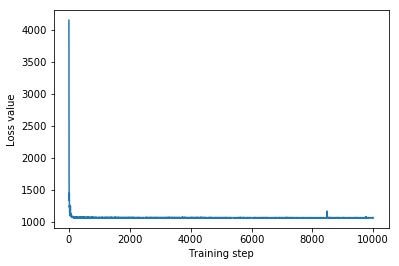
plt.plot(iaf_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
IAF surrogate posterior ELBO: -1065.3663330078125
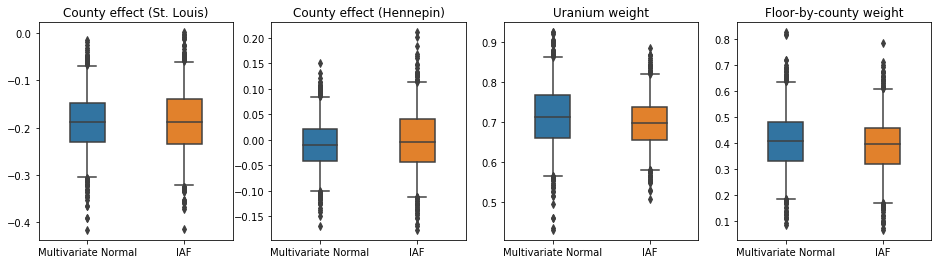
Gli intervalli credibili per il surrogato posteriore IAF appaiono simili a quelli del normale multivariato vincolato.
results['IAF'] = pack_samples(iaf_samples)
plot_boxplot(results)
Linea di base: surrogato di campo medio posteriore
I posteriori surrogati VI sono spesso considerati distribuzioni normali di campo medio (indipendenti), con medie e varianze addestrabili, che sono vincolate al supporto del precedente con una trasformazione biunivoca. Definiamo un surrogato posteriore di campo medio in aggiunta ai due surrogato posteriori più espressivi, utilizzando la stessa formula generale del surrogato normale multivariato posteriore.
# A block-diagonal linear operator, in which each block is a diagonal operator,
# transforms the standard Normal base distribution to produce a mean-field
# surrogate posterior.
operators = (tf.linalg.LinearOperatorDiag,
tf.linalg.LinearOperatorDiag,
tf.linalg.LinearOperatorDiag)
block_diag_linop = (
tfp.experimental.vi.util.build_trainable_linear_operator_block(
operators, flat_event_size))
mean_field_scale = tfb.ScaleMatvecLinearOperatorBlock(block_diag_linop)
mean_field_loc = tfb.JointMap(
tf.nest.map_structure(
lambda s: tfb.Shift(
tf.Variable(tf.random.uniform(
(s,), minval=-2., maxval=2., dtype=tf.float32))),
flat_event_size))
mean_field_surrogate_posterior = tfd.TransformedDistribution(
base_standard_dist,
bijector = tfb.Chain( # Note that the chained bijectors are applied in reverse order
[
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the posterior
reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
mean_field_loc, # allow for nonzero mean
mean_field_scale # apply the block matrix transformation to the standard Normal distribution
]))
optimizer=tf.optimizers.Adam(learning_rate=1e-2)
mean_field_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
mean_field_surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=16,
jit_compile=True)
mean_field_samples = mean_field_surrogate_posterior.sample(1000)
mean_field_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*mean_field_samples)
- mean_field_surrogate_posterior.log_prob(mean_field_samples))
print('Mean-field surrogate posterior ELBO: {}'.format(mean_field_final_elbo))
plt.plot(mean_field_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
Mean-field surrogate posterior ELBO: -1065.7652587890625
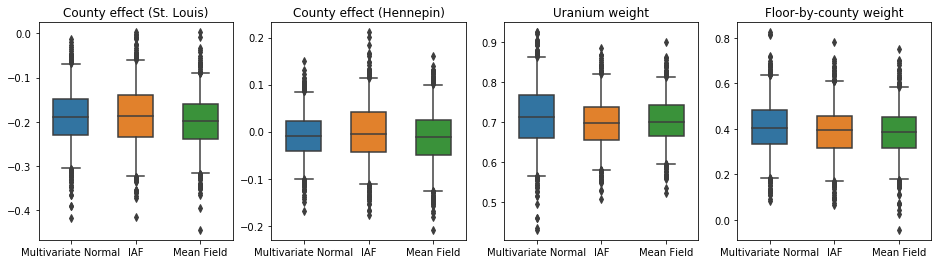
In questo caso, il surrogato del campo medio posteriore fornisce risultati simili ai surrogato posteriori più espressivi, indicando che questo modello più semplice può essere adeguato per il compito di inferenza.
results['Mean Field'] = pack_samples(mean_field_samples)
plot_boxplot(results)
Verità al suolo: Hamiltoniana Monte Carlo (HMC)
Usiamo HMC per generare campioni di "verità a terra" dal vero posteriore, per il confronto con i risultati dei posteriori surrogati.
num_chains = 8
num_leapfrog_steps = 3
step_size = 0.4
num_steps=20000
flat_event_shape = tf.nest.flatten(target_model.event_shape)
enum_components = list(range(len(flat_event_shape)))
bijector = tfb.Restructure(
enum_components,
tf.nest.pack_sequence_as(target_model.event_shape, enum_components))(
target_model.experimental_default_event_space_bijector())
current_state = bijector(
tf.nest.map_structure(
lambda e: tf.zeros([num_chains] + list(e), dtype=tf.float32),
target_model.event_shape))
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_model.unnormalized_log_prob,
num_leapfrog_steps=num_leapfrog_steps,
step_size=[tf.fill(s.shape, step_size) for s in current_state])
hmc = tfp.mcmc.TransformedTransitionKernel(
hmc, bijector)
hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
hmc,
num_adaptation_steps=int(num_steps // 2 * 0.8),
target_accept_prob=0.9)
chain, is_accepted = tf.function(
lambda current_state: tfp.mcmc.sample_chain(
current_state=current_state,
kernel=hmc,
num_results=num_steps // 2,
num_burnin_steps=num_steps // 2,
trace_fn=lambda _, pkr:
(pkr.inner_results.inner_results.is_accepted),
),
autograph=False,
jit_compile=True)(current_state)
accept_rate = tf.reduce_mean(tf.cast(is_accepted, tf.float32))
ess = tf.nest.map_structure(
lambda c: tfp.mcmc.effective_sample_size(
c,
cross_chain_dims=1,
filter_beyond_positive_pairs=True),
chain)
r_hat = tf.nest.map_structure(tfp.mcmc.potential_scale_reduction, chain)
hmc_samples = pack_samples(
tf.nest.pack_sequence_as(target_model.event_shape, chain))
print('Acceptance rate is {}'.format(accept_rate))
Acceptance rate is 0.9008625149726868
Tracciare le tracce del campione per verificare l'integrità dei risultati HMC.
def plot_traces(var_name, samples):
fig, axes = plt.subplots(1, 2, figsize=(14, 1.5), sharex='col', sharey='col')
for chain in range(num_chains):
s = samples.numpy()[:, chain]
axes[0].plot(s, alpha=0.7)
sns.kdeplot(s, ax=axes[1], shade=False)
axes[0].title.set_text("'{}' trace".format(var_name))
axes[1].title.set_text("'{}' distribution".format(var_name))
axes[0].set_xlabel('Iteration')
warnings.filterwarnings('ignore')
for var, var_samples in hmc_samples.items():
plot_traces(var, var_samples)




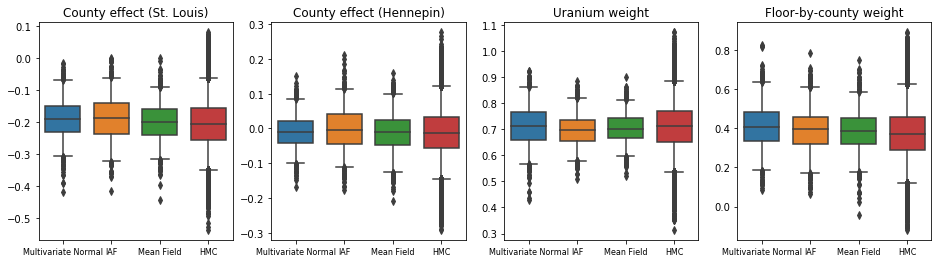
Tutti e tre i posteriori surrogati hanno prodotto intervalli credibili che sono visivamente simili ai campioni HMC, sebbene a volte sottodispersi a causa dell'effetto della perdita ELBO, come è comune in VI.
results['HMC'] = hmc_samples
plot_boxplot(results)
Risultati aggiuntivi
Funzioni di stampa
plt.rcParams.update({'axes.titlesize': 'medium', 'xtick.labelsize': 'medium'})
def plot_loss_and_elbo():
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].scatter([0, 1, 2],
[mvn_final_elbo.numpy(),
iaf_final_elbo.numpy(),
mean_field_final_elbo.numpy()])
axes[0].set_xticks(ticks=[0, 1, 2])
axes[0].set_xticklabels(labels=[
'Multivariate Normal', 'IAF', 'Mean Field'])
axes[0].title.set_text('Evidence Lower Bound (ELBO)')
axes[1].plot(mvn_loss, label='Multivariate Normal')
axes[1].plot(iaf_loss, label='IAF')
axes[1].plot(mean_field_loss, label='Mean Field')
axes[1].set_ylim([1000, 4000])
axes[1].set_xlabel('Training step')
axes[1].set_ylabel('Loss (negative ELBO)')
axes[1].title.set_text('Loss')
plt.legend()
plt.show()
plt.rcParams.update({'axes.titlesize': 'medium', 'xtick.labelsize': 'small'})
def plot_kdes(num_chains=8):
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
k = list(results.values())[0].keys()
plot_results = {
v: {p: results[p][v] for p in results} for v in k}
for i, (var, var_results) in enumerate(plot_results.items()):
ax = axes[i % 2, i // 2]
for posterior, posterior_results in var_results.items():
if posterior == 'HMC':
label = posterior
for chain in range(num_chains):
sns.kdeplot(
posterior_results[:, chain],
ax=ax, shade=False, color='k', linestyle=':', label=label)
label=None
else:
sns.kdeplot(
posterior_results, ax=ax, shade=False, label=posterior)
ax.title.set_text('{}'.format(var))
ax.legend()
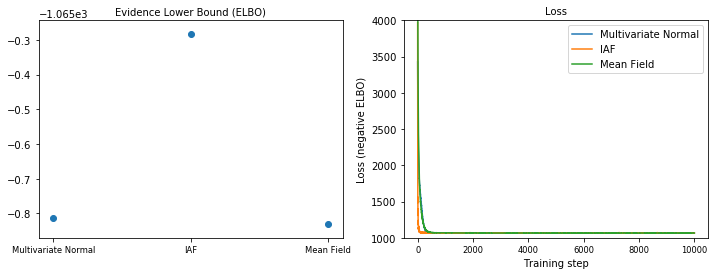
Evidenza limite inferiore (ELBO)
IAF, di gran lunga il surrogato posteriore più grande e più flessibile, converge al limite inferiore di prova più alto (ELBO).
plot_loss_and_elbo()
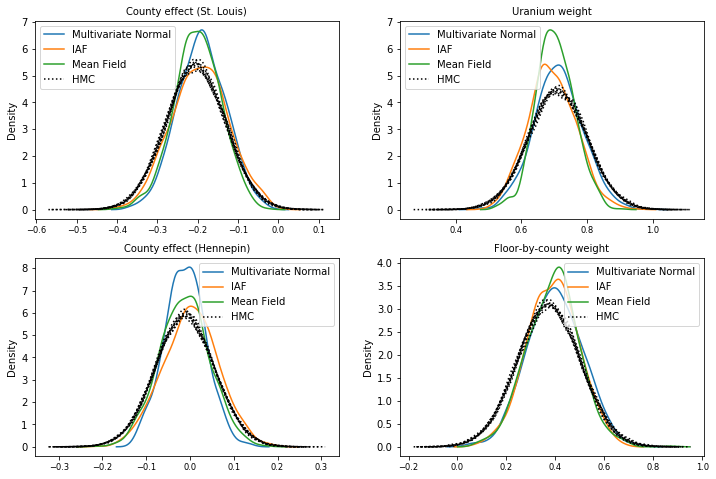
Campioni posteriori
Campioni da ciascun surrogato posteriore, confrontati con campioni di verità al suolo HMC (una diversa visualizzazione dei campioni mostrati nei grafici a scatola).
plot_kdes()
Conclusione
In questo Colab, abbiamo costruito posteriori surrogati VI utilizzando distribuzioni congiunte e biiettori multiparte e li abbiamo adattati per stimare intervalli credibili per i pesi in un modello di regressione sul set di dati del radon. Per questo semplice modello, i posteriori surrogate più espressivi si sono comportati in modo simile a un posteriore surrogato di campo medio. Gli strumenti che abbiamo dimostrato, tuttavia, possono essere utilizzati per costruire un'ampia gamma di posteriori surrogati flessibili adatti a modelli più complessi.
