הסקה וריאציונית על מודלים גרפיים הסתברותיים עם הפצות משותפות

הצג באתר TensorFlow.org

הפעל בגוגל קולאב

צפה במקור ב-GitHub

הורד מחברת

היסק וריאציוני (VI) מטיל מסקנות בייסיאניות משוערות כבעיית אופטימיזציה ומחפש התפלגות אחורית 'תחליף' הממזערת את סטיית ה-KL עם האחורי האמיתי. VI מבוסס גרדיאנט הוא לרוב מהיר יותר משיטות MCMC, מרכיב באופן טבעי עם אופטימיזציה של פרמטרי המודל, ומספק גבול נמוך יותר לעדויות המודל שניתן להשתמש בהן ישירות להשוואת מודלים, אבחון התכנסות והסקת מסקנות ניתנות לחיבור.

TensorFlow Probability מציעה כלים ל-VI מהיר, גמיש וניתן להרחבה המתאימים באופן טבעי לערימת ה-TFP. כלים אלה מאפשרים בנייה של פוסטרים אחוריים עם מבני שיתוף פעולה המושרים על ידי טרנספורמציות ליניאריות או זרימות מנרמלות.

VI יכול לשמש כדי להעריך בייס במרווחים אמינים עבור פרמטרים של מודל רגרסיה להעריך את ההשפעות של טיפולים שונים או תכונות הנצפה על תוצאה של עניין. מרווחים אמינים קושרים את ערכיו של פרמטר בלתי נצפה בהסתברות מסוימת, לפי ההתפלגות האחורית של הפרמטר המותנה בנתונים נצפים ובהנחה על ההתפלגות הקודמת של הפרמטר.

בשנת Colab זו, אנו מדגימים כיצד להשתמש VI להשיג במרווחים אמינים עבור פרמטרים של בייס ליניארית מודל רגרסיה עבור רמות הראדון הנמדד בתים (באמצעות גלמן ואח של (2007) במערך ראדון. ; לראות דוגמאות דומות ב סטן). אנו מדגימים כיצד הפריון הכולל JointDistribution ים לשלב עם bijectors לבנות להתאים שני סוגים של posteriors פונדקאית אקספרסיבי:

• התפלגות נורמלית סטנדרטית שעברה טרנספורמציה על ידי מטריצת בלוק. המטריצה ​​עשויה לשקף עצמאות בין מרכיבים מסוימים של החלק האחורי ותלות בין היתר, מה שמרגיע את ההנחה של שדה ממוצע או שיתוף פעולה אחורי.
• קיבולת גבוהה יותר מורכבת יותר, הפוך זרימת autoregressive .

הפונדקאים האחוריים מאומנים ומשווים לתוצאות מקו הבסיס של פוסטריור פוסטריורי בשדה ממוצע, כמו גם דגימות אמת קרקע ממונטה קרלו המילטון.

סקירה כללית של היסק וריאציוני בייסיאני

נניח שיש לנו את התהליך היצרני הבאים, שבהם \(\theta\) מייצג פרמטרים אקראיים, \(\omega\) מייצג פרמטרים דטרמיניסטיים, ואת \(x_i\) הן תכונות ואת \(y_i\) הם ערכי יעד \(i=1,\ldots,n\) נצפו נקודות נתונים: \ להתחיל {align } &\theta \sim r(\Theta) && \text{(Prior)}\ &\text{for } i = 1 \ldots n: \nonumber \ &\quad y_i \sim p(Y_i|x_i, \theta , \ omega) && \ הטקסט {(סבירות)} \ end {align}

VI מאופיין אז על ידי: $\newcommand{\E}{\operatorname{\mathbb{E} } } \newcommand{\K}{\operatorname{\mathbb{K} } } \newcommand{\defeq}{\overset {\tiny\text{def} }{=} } \DeclareMathOperator*{\argmin}{arg\,min}$

\ להתחיל {align} - \ log p ({y_i} _i ^ n | {x_i} _i ^ n, \ omega) & \ defeq - \ log \ int \ textrm {ד} \ תטא \, r (\ Theta) \ prod_i^np(y_i|x_i,\theta, \omega) && \text{(ממש קשה אינטגרל)} \ &= -\log \int \textrm{d}\theta\, q(\theta) \frac{1 }{q(\theta)} r(\theta) \prod_i^np(y_i|x_i,\theta, \omega) && \text{(הכפל ב-1)}\ &\le - \int \textrm{d} \ תטא \, q (\ Theta) \ log \ frac {r (\ Theta) \ prod_i ^ NP (y_i | x i, \ תטא, \ omega)} {q (\ Theta)} && \ הטקסט {(אי-שוויון ינסן )} \ & \ defeq \ E {q (\ Theta)} [- \ log p (y_i | x_i, \ תטא, \ omega)] + \ K [q (\ Theta), r (\ Theta)] \ & \ defeq \text{expected negative log likelihood"} + \ טקסט {KL regularizer"} \ end {align}

(מבחינה טכנית אנחנו מניחים \(q\) הוא בהחלט רציף ביחס \(r\). ראו גם, אי-שוויון ינסן .)

מכיוון שהגבול תקף עבור כל q, הוא ללא ספק הדוק ביותר עבור:

\[q^*,w^* = \argmin_{q \in \mathcal{Q},\omega\in\mathbb{R}^d} \left\{ \sum_i^n\E_{q(\Theta)}\left[ -\log p(y_i|x_i,\Theta, \omega) \right] + \K[q(\Theta), r(\Theta)] \right\}\]

לגבי טרמינולוגיה, אנחנו קוראים

• \(q^*\) את "אחורי פונדקאית," ו,
• \(\mathcal{Q}\) "משפחה פונדקאית."

\(\omega^*\) מייצג את הערכים-ראות מרבית הפרמטרים הדטרמיניסטיים על האובדן השישי. ראה סקר זה לקבלת מידע נוסף על היקש וריאציה.

דוגמה: רגרסיה לינארית היררכית בייסיאנית על מדידות ראדון

ראדון הוא גז רדיואקטיבי החודר לבתים דרך נקודות מגע עם הקרקע. זהו חומר מסרטן המהווה את הגורם העיקרי לסרטן ריאות אצל לא מעשנים. רמות הראדון משתנות מאוד ממשק בית למשק בית.

ה-EPA ערכה מחקר של רמות ראדון ב-80,000 בתים. שני מנבאים חשובים הם:

• קומה בה נעשתה המדידה (ראדון גבוה יותר במרתפים)
• רמת האורניום במחוז (מתאם חיובי עם רמות הראדון)

חיזוי רמות ראדון בבתים מקובצים לפי המחוז היא בעיה קלאסית מודלים היררכיים בייס, הציג גלמן והגבעה (2006) . נבנה מודל ליניארי היררכי לניבוי מדידות ראדון בבתים, שבו ההיררכיה היא קיבוץ הבתים לפי מחוז. אנו מעוניינים במרווחים אמינים להשפעת המיקום (מחוז) על רמת הראדון של בתים במינסוטה. על מנת לבודד את האפקט הזה, נכללות במודל גם ההשפעות של רמת הרצפה והאורניום. בנוסף, נשלב אפקט קונטקסטואלי התואם לקומה הממוצעת שבה בוצעה המדידה, לפי מחוז, כך שאם יש שונות בין המחוזות של הקומה שבה בוצעו המדידות, הדבר אינו מיוחס להשפעה המחוזית.

pip3 install -q tf-nightly tfp-nightly

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow as tf
import tensorflow_datasets as tfds
import tensorflow_probability as tfp
import warnings

tfd = tfp.distributions
tfb = tfp.bijectors

plt.rcParams['figure.facecolor'] = '1.'

# Load the Radon dataset from `tensorflow_datasets` and filter to data from
# Minnesota.
dataset = tfds.as_numpy(
    tfds.load('radon', split='train').filter(
        lambda x: x['features']['state'] == 'MN').batch(10**9))

# Dependent variable: Radon measurements by house.
dataset = next(iter(dataset))
radon_measurement = dataset['activity'].astype(np.float32)
radon_measurement[radon_measurement <= 0.] = 0.1
log_radon = np.log(radon_measurement)

# Measured uranium concentrations in surrounding soil.
uranium_measurement = dataset['features']['Uppm'].astype(np.float32)
log_uranium = np.log(uranium_measurement)

# County indicator.
county_strings = dataset['features']['county'].astype('U13')
unique_counties, county = np.unique(county_strings, return_inverse=True)
county = county.astype(np.int32)
num_counties = unique_counties.size

# Floor on which the measurement was taken.
floor_of_house = dataset['features']['floor'].astype(np.int32)

# Average floor by county (contextual effect).
county_mean_floor = []
for i in range(num_counties):
  county_mean_floor.append(floor_of_house[county == i].mean())
county_mean_floor = np.array(county_mean_floor, dtype=log_radon.dtype)
floor_by_county = county_mean_floor[county]

מודל הרגרסיה מוגדר כדלקמן:

\(\newcommand{\Normal}{\operatorname{\sf Normal} }\)\ להתחיל {align} & \ הטקסט {uranium_weight} \ sim \ Normal (0, 1) \ & \ הטקסט {county_floor_weight} \ sim \ Normal (0, 1) \ & \ הטקסט {עבור} j = 1 \ ldots \text{num_counties}:\ &\quad \text{county_effect}_j \sim \Normal (0, \sigma_c)\ &\text{for } i = 1\ldots n:\ &\quad \mu_i = ( \ & \ quad \ quad \ הטקסט {הטיה} \ & \ quad \ quad + \ הטקסט {אפקט המחוז} {text \ {המחוז} _i} \ & \ quad \ quad + \ הטקסט {log_uranium} _i \ טקסט \ פעמים {uranium_weight } \ & \ quad \ quad + \ הטקסט {floor_of_house} _i \ טקסט \ פעמים {floor_weight} \ & \ quad \ quad + \ הטקסט {המחוז floor_by} {text \ {המחוז} _i} \ טקסט \ פעמים {county_floor_weight}) \ & \ quad \ הטקסט {log_radon} _i \ sim \ Normal (\ mu_i, \ sigma_y) \ end {align} שבו \(i\) אינדקסים התצפיות \(\text{county}_i\) הוא המחוז שבו \(i\)ה תצפית היה נלקח.

אנו משתמשים באפקט אקראי ברמת המחוז כדי ללכוד שונות גיאוגרפית. הפרמטרים uranium_weight ו county_floor_weight הם מודל הסתברותי, ו floor_weight ואת קבוע bias הם דטרמיניסטיים. בחירות הדוגמנות הללו הן שרירותיות ברובן, והן נעשות במטרה להדגים את VI על מודל הסתברותי בעל מורכבות סבירה. לדיון מעמיק יותר של מודלים מדורגים עם השפעות קבוע אקראיות פריון כולל, באמצעות מערך הנתונים ראדון, לראות פריימר דוגמנות מדורגת ואת ההתאמה הכללית Linear Mixed-תופעות מודלים באמצעות הסקת וריאציה .

# Create variables for fixed effects.
floor_weight = tf.Variable(0.)
bias = tf.Variable(0.)

# Variables for scale parameters.
log_radon_scale = tfp.util.TransformedVariable(1., tfb.Exp())
county_effect_scale = tfp.util.TransformedVariable(1., tfb.Exp())

# Define the probabilistic graphical model as a JointDistribution.
@tfd.JointDistributionCoroutineAutoBatched
def model():
  uranium_weight = yield tfd.Normal(0., scale=1., name='uranium_weight')
  county_floor_weight = yield tfd.Normal(
      0., scale=1., name='county_floor_weight')
  county_effect = yield tfd.Sample(
      tfd.Normal(0., scale=county_effect_scale),
      sample_shape=[num_counties], name='county_effect')
  yield tfd.Normal(
      loc=(log_uranium * uranium_weight + floor_of_house* floor_weight
           + floor_by_county * county_floor_weight
           + tf.gather(county_effect, county, axis=-1)
           + bias),
      scale=log_radon_scale[..., tf.newaxis],
      name='log_radon') 

# Pin the observed `log_radon` values to model the un-normalized posterior.
target_model = model.experimental_pin(log_radon=log_radon)

פוסטריורס אקספרסיבי

לאחר מכן, אנו מעריכים את ההתפלגות האחורית של ההשפעות האקראיות באמצעות VI עם שני סוגים שונים של פוסטריוריים אחוריים:

• התפלגות נורמלית רב-משתנית מוגבלת, עם מבנה קוווריאציה המושרה על ידי טרנספורמציה של מטריצה ​​בלוק.
• פונקצית התפלגות רבה נורמאלי הסטנדרטי טרנספורמציה על ידי Flow AutoRegressive הפוך , אשר מחולק אז מחדש כדי להתאים את התמיכה של האחוריים.

רב משתנים תחליף נורמלי אחורי

כדי לבנות את הפונדקאי האחורי הזה, נעשה שימוש באופרטור ליניארי הניתן לאימון כדי לעורר מתאם בין מרכיבי החלק האחורי.

# Determine the `event_shape` of the posterior, and calculate the size of each
# `event_shape` component. These determine the sizes of the components of the
# underlying standard Normal distribution, and the dimensions of the blocks in
# the blockwise matrix transformation.
event_shape = target_model.event_shape_tensor()
flat_event_shape = tf.nest.flatten(event_shape)
flat_event_size = tf.nest.map_structure(tf.reduce_prod, flat_event_shape)

# The `event_space_bijector` maps unconstrained values (in R^n) to the support
# of the prior -- we'll need this at the end to constrain Multivariate Normal
# samples to the prior's support.
event_space_bijector = target_model.experimental_default_event_space_bijector()

לבנות JointDistribution עם רכיבים רגילים סטנדרטיים מוערך וקטור, עם גדלים שקבעו רכיבים לפני המתאימים. הרכיבים צריכים להיות בעלי ערך וקטור כדי שיוכלו לעבור טרנספורמציה על ידי האופרטור הליניארי.

base_standard_dist = tfd.JointDistributionSequential(
      [tfd.Sample(tfd.Normal(0., 1.), s) for s in flat_event_size])

בנו אופרטור ליניארי תחתון-משולש הניתן לאילוף בלוק. ניישם אותו על ההתפלגות הנורמלית הסטנדרטית כדי ליישם טרנספורמציה של מטריצה ​​(ניתנת לאימון) של מטריצה ​​בלוק ולעורר את מבנה המתאם של החלק האחורי.

בתוך המפעיל ליניארי blockwise, בלוק מלא מטריקס שאפשר לאלף מייצג שונה משותף מלא בין שני מרכיבים של האחוריים, ואילו גוש אפסים (או None ) מבטא עצמאות. בלוקים באלכסון הם מטריצות משולשות נמוכות יותר או אלכסוניות, כך שכל מבנה הבלוק מייצג מטריצה ​​משולשת נמוכה יותר.

החלת הביוקטור הזה על התפלגות הבסיס מביאה להתפלגות נורמלית רב-משתנית עם ממוצע 0 ו-(Cholesky-factories) שיתופיות שווה למטריצת הבלוק המשולש התחתון.

operators = (
    (tf.linalg.LinearOperatorDiag,),  # Variance of uranium weight (scalar).
    (tf.linalg.LinearOperatorFullMatrix,  # Covariance between uranium and floor-by-county weights.
     tf.linalg.LinearOperatorDiag),  # Variance of floor-by-county weight (scalar).
    (None,  # Independence between uranium weight and county effects.
     None,  #  Independence between floor-by-county and county effects.
     tf.linalg.LinearOperatorDiag)  # Independence among the 85 county effects.
    )

block_tril_linop = (
    tfp.experimental.vi.util.build_trainable_linear_operator_block(
        operators, flat_event_size))
scale_bijector = tfb.ScaleMatvecLinearOperatorBlock(block_tril_linop)

לאחר החלת מפעיל ליניארי ל בהתפלגות נורמלית סטנדרטית, להחיל מרובה חלקים Shift bijector לאפשר מתכוון לקחת ערכים שונה מאפס.

loc_bijector = tfb.JointMap(
    tf.nest.map_structure(
        lambda s: tfb.Shift(
            tf.Variable(tf.random.uniform(
                (s,), minval=-2., maxval=2., dtype=tf.float32))),
        flat_event_size))

יש לעצב מחדש ולבנות מחדש את ההתפלגות הנורמלית הרב-משתנית, המתקבלת על-ידי הפיכת התפלגות הנורמלית הסטנדרטית עם קנה המידה והמיקום, כך שיתאים לקודם, ולבסוף להגביל את התמיכה בקודקוד.

# Reshape each component to match the prior, using a nested structure of
# `Reshape` bijectors wrapped in `JointMap` to form a multipart bijector.
reshape_bijector = tfb.JointMap(
    tf.nest.map_structure(tfb.Reshape, flat_event_shape))

# Restructure the flat list of components to match the prior's structure
unflatten_bijector = tfb.Restructure(
        tf.nest.pack_sequence_as(
            event_shape, range(len(flat_event_shape))))

כעת, חבר את הכל יחד - שרשרת את ה-bijectors הניתנים לאימון יחד והחל אותם על התפלגות הרגילה הבסיסית כדי לבנות את הפונדקאי האחורי.

surrogate_posterior = tfd.TransformedDistribution(
    base_standard_dist,
    bijector = tfb.Chain(  # Note that the chained bijectors are applied in reverse order
        [
         event_space_bijector,  # constrain the surrogate to the support of the prior
         unflatten_bijector,  # pack the reshaped components into the `event_shape` structure of the posterior
         reshape_bijector,  # reshape the vector-valued components to match the shapes of the posterior components
         loc_bijector,  # allow for nonzero mean
         scale_bijector  # apply the block matrix transformation to the standard Normal distribution
         ]))

אמן את הפונדקאית הרגילה הרב-משתנית האחורית.

optimizer = tf.optimizers.Adam(learning_rate=1e-2)
mvn_loss = tfp.vi.fit_surrogate_posterior(
    target_model.unnormalized_log_prob,
    surrogate_posterior,
    optimizer=optimizer,
    num_steps=10**4,
    sample_size=16,
    jit_compile=True)

mvn_samples = surrogate_posterior.sample(1000)
mvn_final_elbo = tf.reduce_mean(
    target_model.unnormalized_log_prob(*mvn_samples)
    - surrogate_posterior.log_prob(mvn_samples))

print('Multivariate Normal surrogate posterior ELBO: {}'.format(mvn_final_elbo))

plt.plot(mvn_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')

Multivariate Normal surrogate posterior ELBO: -1065.705322265625

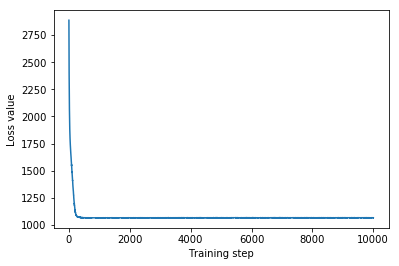
מכיוון שהפוסטריורית המאומנת היא הפצת TFP, אנו יכולים לקחת ממנה דגימות ולעבד אותן כדי לייצר מרווחים אחוריים אמינים עבור הפרמטרים.

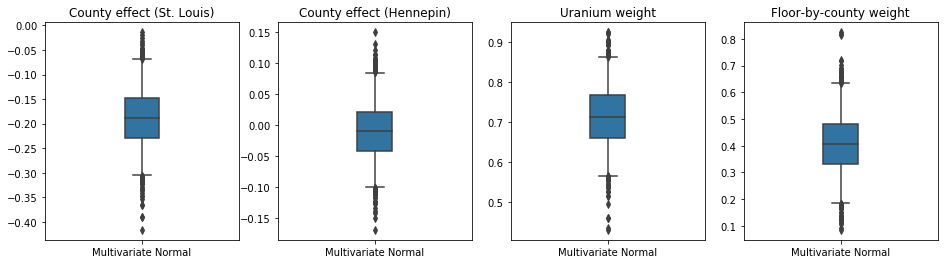
מגרשי שפם התיבה-ו-להלן מציגים 50% ו 95% מרווחיים אמינה להשפעת המחוז של שני המחוזות הגדולים ואת המשקולות רגרסיה על מדידות אורניום קרקע והקומה ממוצעת ידי מחוז. המרווחים האמינים האחוריים להשפעות המחוז מצביעים על כך שהמיקום במחוז סנט לואיס קשור לרמות ראדון נמוכות יותר, לאחר שהתייחסו למשתנים אחרים, ושהשפעת המיקום במחוז הנפין כמעט נייטרלית.

מרווחים אמינים אחוריים על משקלי הרגרסיה מראים שרמות גבוהות יותר של אורניום בקרקע קשורות לרמות גבוהות יותר של ראדון, ומחוזות שבהם בוצעו מדידות בקומות גבוהות יותר (כנראה בגלל שלבית לא היה מרתף) נוטים להיות בעלי רמות גבוהות יותר של ראדון, שיכול להתייחס לתכונות הקרקע והשפעתם על סוג המבנים שנבנו.

המקדם (הדטרמיניסטי) של הרצפה הוא שלילי, מה שמעיד כי בקומות נמוכות יש רמות ראדון גבוהות יותר, כצפוי.

st_louis_co = 69  # Index of St. Louis, the county with the most observations.
hennepin_co = 25  # Index of Hennepin, with the second-most observations.

def pack_samples(samples):
  return {'County effect (St. Louis)': samples.county_effect[..., st_louis_co],
          'County effect (Hennepin)': samples.county_effect[..., hennepin_co],
          'Uranium weight': samples.uranium_weight,
          'Floor-by-county weight': samples.county_floor_weight}

def plot_boxplot(posterior_samples):
  fig, axes = plt.subplots(1, 4, figsize=(16, 4))

  # Invert the results dict for easier plotting.
  k = list(posterior_samples.values())[0].keys()
  plot_results = {
      v: {p: posterior_samples[p][v] for p in posterior_samples} for v in k}
  for i, (var, var_results) in enumerate(plot_results.items()):
    sns.boxplot(data=list(var_results.values()), ax=axes[i],
                width=0.18*len(var_results), whis=(2.5, 97.5))
    # axes[i].boxplot(list(var_results.values()), whis=(2.5, 97.5))
    axes[i].title.set_text(var)
    fs = 10 if len(var_results) < 4 else 8
    axes[i].set_xticklabels(list(var_results.keys()), fontsize=fs)

results = {'Multivariate Normal': pack_samples(mvn_samples)}

print('Bias is: {:.2f}'.format(bias.numpy()))
print('Floor fixed effect is: {:.2f}'.format(floor_weight.numpy()))
plot_boxplot(results)

Bias is: 1.40
Floor fixed effect is: -0.72

Inverse Autoregressive Flow תחליף אחורי

זרימות אוטומטיות הפוכות (IAFs) הן זרימות מנרמלות המשתמשות ברשתות עצביות כדי ללכוד תלות מורכבת ולא ליניארית בין מרכיבי ההתפלגות. לאחר מכן, אנו בונים חליפת חיל האוויר האחורית כדי לראות אם המודל בעל הקיבולת הגבוהה והגמיש יותר מתעלה על הרגיל הרב-משתני המוגבל.

# Build a standard Normal with a vector `event_shape`, with length equal to the
# total number of degrees of freedom in the posterior.
base_distribution = tfd.Sample(
    tfd.Normal(0., 1.), sample_shape=[tf.reduce_sum(flat_event_size)])

# Apply an IAF to the base distribution.
num_iafs = 2
iaf_bijectors = [
    tfb.Invert(tfb.MaskedAutoregressiveFlow(
        shift_and_log_scale_fn=tfb.AutoregressiveNetwork(
            params=2, hidden_units=[256, 256], activation='relu')))
    for _ in range(num_iafs)
]

# Split the base distribution's `event_shape` into components that are equal
# in size to the prior's components.
split = tfb.Split(flat_event_size)

# Chain these bijectors and apply them to the standard Normal base distribution
# to build the surrogate posterior. `event_space_bijector`,
# `unflatten_bijector`, and `reshape_bijector` are the same as in the
# multivariate Normal surrogate posterior.
iaf_surrogate_posterior = tfd.TransformedDistribution(
    base_distribution,
    bijector=tfb.Chain([
         event_space_bijector,  # constrain the surrogate to the support of the prior
         unflatten_bijector,  # pack the reshaped components into the `event_shape` structure of the prior
         reshape_bijector,  # reshape the vector-valued components to match the shapes of the prior components
         split] +  # Split the samples into components of the same size as the prior components
         iaf_bijectors  # Apply a flow model to the Tensor-valued standard Normal distribution
         ))

אמן את הפונדקאית של חיל האוויר האחורי.

optimizer=tf.optimizers.Adam(learning_rate=1e-2)
iaf_loss = tfp.vi.fit_surrogate_posterior(
  target_model.unnormalized_log_prob,
  iaf_surrogate_posterior,
  optimizer=optimizer,
  num_steps=10**4,
  sample_size=4,
  jit_compile=True)

iaf_samples = iaf_surrogate_posterior.sample(1000)
iaf_final_elbo = tf.reduce_mean(
    target_model.unnormalized_log_prob(*iaf_samples)
    - iaf_surrogate_posterior.log_prob(iaf_samples))
print('IAF surrogate posterior ELBO: {}'.format(iaf_final_elbo))

plt.plot(iaf_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')

IAF surrogate posterior ELBO: -1065.3663330078125

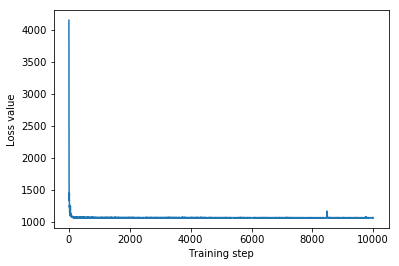
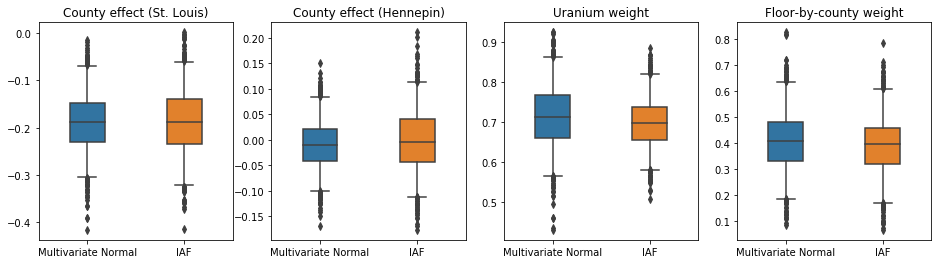
המרווחים האמינים עבור הפונדקאית האחורית של חיל האוויר נראים דומים לאלו של הנורמלי הרב-משתני המוגבל.

results['IAF'] = pack_samples(iaf_samples)
plot_boxplot(results)

קו בסיס: פונדקאי שדה ממוצע אחורי

מניחים לעתים קרובות שהחלקים האחוריים של VI פונדקאים הם התפלגות נורמלית של שדה ממוצע (בלתי תלוי), עם אמצעים ושונות ניתנים לאימון, המוגבלים לתמיכה של הקודמת עם טרנספורמציה נבנית. אנו מגדירים פוסטריור פוסטריורי בשדה ממוצע בנוסף לשני הפונדקאיים האחוריים האקספרסיביים יותר, תוך שימוש באותה נוסחה כללית כמו פוסטריור נורמאלי רב משתנים.

# A block-diagonal linear operator, in which each block is a diagonal operator,
# transforms the standard Normal base distribution to produce a mean-field
# surrogate posterior.
operators = (tf.linalg.LinearOperatorDiag,
             tf.linalg.LinearOperatorDiag,
             tf.linalg.LinearOperatorDiag)
block_diag_linop = (
    tfp.experimental.vi.util.build_trainable_linear_operator_block(
        operators, flat_event_size))
mean_field_scale = tfb.ScaleMatvecLinearOperatorBlock(block_diag_linop)

mean_field_loc = tfb.JointMap(
    tf.nest.map_structure(
        lambda s: tfb.Shift(
            tf.Variable(tf.random.uniform(
                (s,), minval=-2., maxval=2., dtype=tf.float32))),
        flat_event_size))

mean_field_surrogate_posterior = tfd.TransformedDistribution(
    base_standard_dist,
    bijector = tfb.Chain(  # Note that the chained bijectors are applied in reverse order
        [
         event_space_bijector,  # constrain the surrogate to the support of the prior
         unflatten_bijector,  # pack the reshaped components into the `event_shape` structure of the posterior
         reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
         mean_field_loc,   # allow for nonzero mean
         mean_field_scale  # apply the block matrix transformation to the standard Normal distribution
         ]))

optimizer=tf.optimizers.Adam(learning_rate=1e-2)
mean_field_loss = tfp.vi.fit_surrogate_posterior(
    target_model.unnormalized_log_prob,
    mean_field_surrogate_posterior,
    optimizer=optimizer,
    num_steps=10**4,
    sample_size=16,
    jit_compile=True)

mean_field_samples = mean_field_surrogate_posterior.sample(1000)
mean_field_final_elbo = tf.reduce_mean(
    target_model.unnormalized_log_prob(*mean_field_samples)
    - mean_field_surrogate_posterior.log_prob(mean_field_samples))
print('Mean-field surrogate posterior ELBO: {}'.format(mean_field_final_elbo))

plt.plot(mean_field_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')

Mean-field surrogate posterior ELBO: -1065.7652587890625

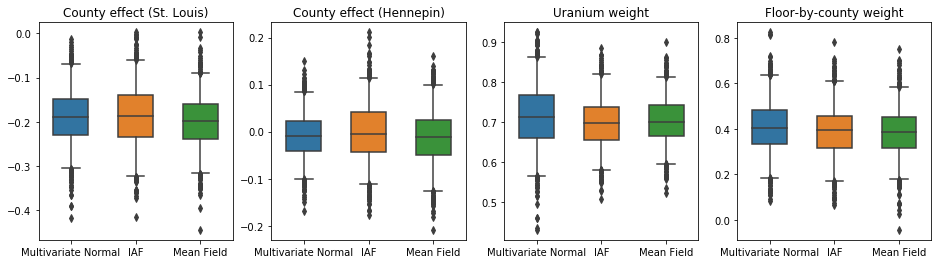
במקרה זה, הפונדקאי הממוצע האחורי של השדה נותן תוצאות דומות לאחורי הפונדקאית האקספרסיביים יותר, מה שמצביע על כך שהמודל הפשוט יותר הזה עשוי להתאים למשימת ההסקה.

results['Mean Field'] = pack_samples(mean_field_samples)
plot_boxplot(results)

האמת הבסיסית: המילטון מונטה קרלו (HMC)

אנו משתמשים ב-HMC כדי ליצור דגימות של "אמת קרקע" מהחלק האחורי האמיתי, לצורך השוואה עם תוצאות הפונדקאיות האחוריות.

num_chains = 8
num_leapfrog_steps = 3
step_size = 0.4
num_steps=20000

flat_event_shape = tf.nest.flatten(target_model.event_shape)
enum_components = list(range(len(flat_event_shape)))
bijector = tfb.Restructure(
    enum_components,
    tf.nest.pack_sequence_as(target_model.event_shape, enum_components))(
        target_model.experimental_default_event_space_bijector())

current_state = bijector(
    tf.nest.map_structure(
        lambda e: tf.zeros([num_chains] + list(e), dtype=tf.float32),
    target_model.event_shape))

hmc = tfp.mcmc.HamiltonianMonteCarlo(
    target_log_prob_fn=target_model.unnormalized_log_prob,
    num_leapfrog_steps=num_leapfrog_steps,
    step_size=[tf.fill(s.shape, step_size) for s in current_state])

hmc = tfp.mcmc.TransformedTransitionKernel(
    hmc, bijector)
hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
    hmc,
    num_adaptation_steps=int(num_steps // 2 * 0.8),
    target_accept_prob=0.9)

chain, is_accepted = tf.function(
    lambda current_state: tfp.mcmc.sample_chain(
        current_state=current_state,
        kernel=hmc,
        num_results=num_steps // 2,
        num_burnin_steps=num_steps // 2,
        trace_fn=lambda _, pkr:
        (pkr.inner_results.inner_results.is_accepted),
        ),
    autograph=False,
    jit_compile=True)(current_state)

accept_rate = tf.reduce_mean(tf.cast(is_accepted, tf.float32))
ess = tf.nest.map_structure(
    lambda c: tfp.mcmc.effective_sample_size(
        c,
        cross_chain_dims=1,
        filter_beyond_positive_pairs=True),
    chain)

r_hat = tf.nest.map_structure(tfp.mcmc.potential_scale_reduction, chain)
hmc_samples = pack_samples(
    tf.nest.pack_sequence_as(target_model.event_shape, chain))
print('Acceptance rate is {}'.format(accept_rate))

Acceptance rate is 0.9008625149726868

תכנן עקבות מדגם כדי לבדוק את תוצאות HMC.

def plot_traces(var_name, samples):
  fig, axes = plt.subplots(1, 2, figsize=(14, 1.5), sharex='col', sharey='col')
  for chain in range(num_chains):
    s = samples.numpy()[:, chain]
    axes[0].plot(s, alpha=0.7)
    sns.kdeplot(s, ax=axes[1], shade=False)
    axes[0].title.set_text("'{}' trace".format(var_name))
    axes[1].title.set_text("'{}' distribution".format(var_name))
    axes[0].set_xlabel('Iteration')

warnings.filterwarnings('ignore')
for var, var_samples in hmc_samples.items():
  plot_traces(var, var_samples)

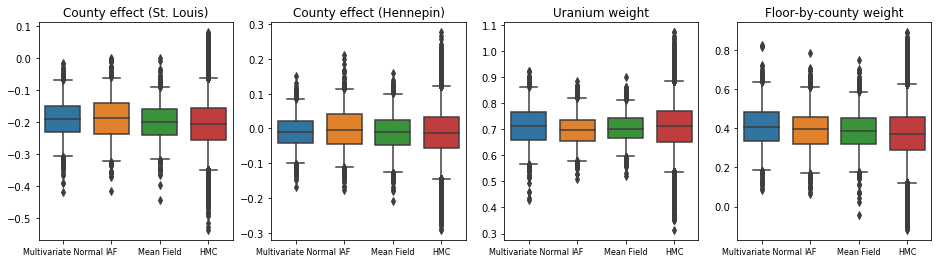
כל שלושת האחוריים הפונדקאיים יצרו מרווחים אמינים הדומים מבחינה ויזואלית לדגימות ה-HMC, אם כי לפעמים מפוזרות בחסר עקב השפעת אובדן ה-ELBO, כפי שמקובל ב-VI.

results['HMC'] = hmc_samples
plot_boxplot(results)

תוצאות נוספות

פונקציות תכנון

plt.rcParams.update({'axes.titlesize': 'medium', 'xtick.labelsize': 'medium'})
def plot_loss_and_elbo():
  fig, axes = plt.subplots(1, 2, figsize=(12, 4))

  axes[0].scatter([0, 1, 2],
                  [mvn_final_elbo.numpy(),
                  iaf_final_elbo.numpy(),
                  mean_field_final_elbo.numpy()])
  axes[0].set_xticks(ticks=[0, 1, 2])
  axes[0].set_xticklabels(labels=[
    'Multivariate Normal', 'IAF', 'Mean Field'])
  axes[0].title.set_text('Evidence Lower Bound (ELBO)')

  axes[1].plot(mvn_loss, label='Multivariate Normal')
  axes[1].plot(iaf_loss, label='IAF')
  axes[1].plot(mean_field_loss, label='Mean Field')
  axes[1].set_ylim([1000, 4000])
  axes[1].set_xlabel('Training step')
  axes[1].set_ylabel('Loss (negative ELBO)')
  axes[1].title.set_text('Loss')
  plt.legend()
  plt.show()

plt.rcParams.update({'axes.titlesize': 'medium', 'xtick.labelsize': 'small'})
def plot_kdes(num_chains=8):
  fig, axes = plt.subplots(2, 2, figsize=(12, 8))
  k = list(results.values())[0].keys()
  plot_results = {
      v: {p: results[p][v] for p in results} for v in k}
  for i, (var, var_results) in enumerate(plot_results.items()):
    ax = axes[i % 2, i // 2]
    for posterior, posterior_results in var_results.items():
      if posterior == 'HMC':
        label = posterior
        for chain in range(num_chains):
          sns.kdeplot(
              posterior_results[:, chain],
              ax=ax, shade=False, color='k', linestyle=':', label=label)
          label=None
      else:
        sns.kdeplot(
            posterior_results, ax=ax, shade=False, label=posterior)
        ax.title.set_text('{}'.format(var))
    ax.legend()

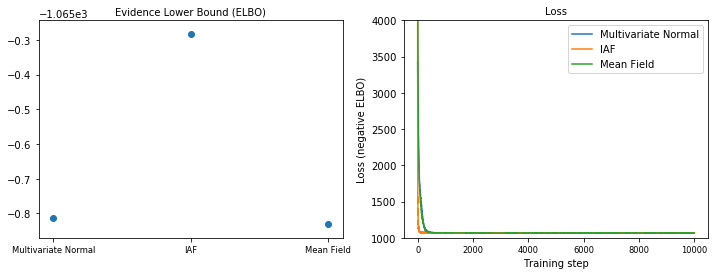
הגבול התחתון של ראיות (ELBO)

חיל האוויר, ללא ספק הפונדקאית האחורית הגדולה והגמישה ביותר, מתכנסת לגבול התחתון של הראיות הגבוה ביותר (ELBO).

plot_loss_and_elbo()

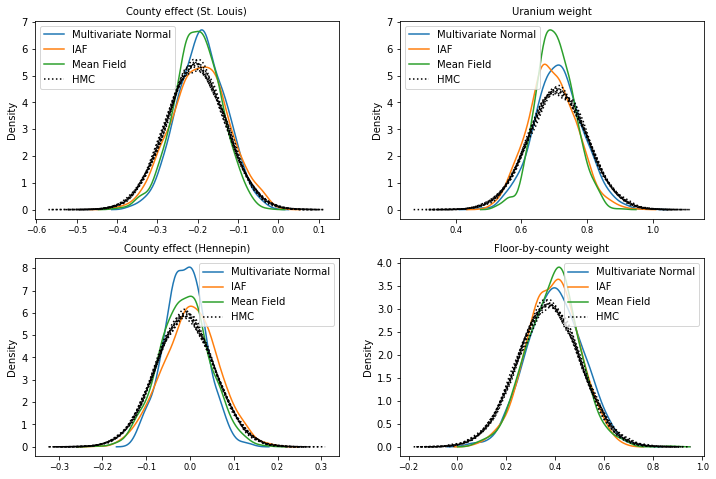
דוגמאות אחוריות

דגימות מכל פונדקאי אחורי, בהשוואה לדגימות אמת קרקע של HMC (הדמיה שונה של הדגימות המוצגות בחלקות הקופסה).

plot_kdes()

סיכום

ב-Colab הזה, בנינו חלל VI אחוריים תוך שימוש בהפצות מפרקים וביג'קטורים מרובי חלקים, ומתאימים אותם להערכת מרווחים אמינים למשקלים במודל רגרסיה על מערך הנתונים של הראדון. עבור המודל הפשוט הזה, פוסטיוריות פוסטיוריות אקספרסיביות יותר בוצעו בדומה לפונדקאית פוסטריור בשדה ממוצע. עם זאת, הכלים שהדגמנו יכולים לשמש לבניית מגוון רחב של חליפות פוסטר גמישות המתאימים לדגמים מורכבים יותר.