 Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
TensorFlow Xác suất (TFP) là một thư viện cho lập luận xác suất và thống kê phân tích mà bây giờ cũng hoạt động trên JAX ! Đối với những người không quen thuộc, JAX là một thư viện dành cho tính toán số tăng tốc dựa trên các phép biến đổi hàm có thể tổng hợp.
TFP trên JAX hỗ trợ rất nhiều chức năng hữu ích nhất của TFP thông thường trong khi vẫn bảo toàn các tính năng trừu tượng và API mà nhiều người dùng TFP hiện đang cảm thấy thoải mái.
Thành lập
TFP trên JAX không phụ thuộc vào TensorFlow; hãy gỡ cài đặt hoàn toàn TensorFlow khỏi Colab này.
pip uninstall tensorflow -y -q
Chúng tôi có thể cài đặt TFP trên JAX với các bản dựng hàng đêm mới nhất của TFP.
pip install -Uq tfp-nightly[jax] > /dev/null
Hãy nhập một số thư viện Python hữu ích.
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn import datasets
sns.set(style='white')
/usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead. import pandas.util.testing as tm
Hãy cũng nhập một số chức năng JAX cơ bản.
import jax.numpy as jnp
from jax import grad
from jax import jit
from jax import random
from jax import value_and_grad
from jax import vmap
Nhập TFP trên JAX
Để sử dụng TFP trên JAX, chỉ cần nhập jax "bề mặt" và sử dụng nó như bạn thường sẽ tfp :
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
tfpk = tfp.math.psd_kernels
Demo: Hồi quy logistic Bayes
Để chứng minh những gì chúng tôi có thể làm với chương trình phụ trợ JAX, chúng tôi sẽ triển khai hồi quy logistic Bayes được áp dụng cho tập dữ liệu Iris cổ điển.
Đầu tiên, hãy nhập tập dữ liệu Iris và trích xuất một số siêu dữ liệu.
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
Chúng ta có thể xác định các mô hình sử dụng tfd.JointDistributionCoroutine . Chúng tôi sẽ đưa priors bình thường tiêu chuẩn trên cả trọng lượng và thời hạn thiên vị sau đó viết một target_log_prob chức năng ghim nhãn lấy mẫu để các dữ liệu.
Root = tfd.JointDistributionCoroutine.Root
def model():
w = yield Root(tfd.Sample(tfd.Normal(0., 1.),
sample_shape=(num_features, num_classes)))
b = yield Root(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(num_classes,)))
logits = jnp.dot(features, w) + b
yield tfd.Independent(tfd.Categorical(logits=logits),
reinterpreted_batch_ndims=1)
dist = tfd.JointDistributionCoroutine(model)
def target_log_prob(*params):
return dist.log_prob(params + (labels,))
Chúng tôi lấy mẫu từ dist để tạo ra một trạng thái ban đầu cho MCMC. Sau đó, chúng ta có thể xác định một hàm nhận một khóa ngẫu nhiên và một trạng thái ban đầu, và tạo ra 500 mẫu từ Bộ lấy mẫu Không-U-Turn-Sampler (NUTS). Lưu ý rằng chúng ta có thể sử dụng biến đổi JAX như jit biên dịch sampler NUTS của chúng tôi sử dụng XLA.
init_key, sample_key = random.split(random.PRNGKey(0))
init_params = tuple(dist.sample(seed=init_key)[:-1])
@jit
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-3)
return tfp.mcmc.sample_chain(500,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
num_burnin_steps=500,
seed=key)
states, log_probs = run_chain(sample_key, init_params)
plt.figure()
plt.plot(log_probs)
plt.ylabel('Target Log Prob')
plt.xlabel('Iterations of NUTS')
plt.show()
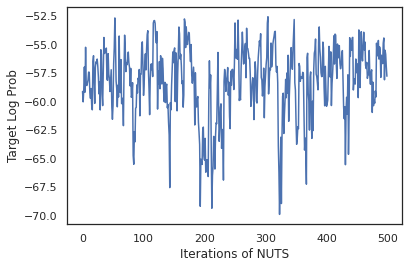
Hãy sử dụng các mẫu của chúng tôi để thực hiện tính trung bình theo mô hình Bayesian (BMA) bằng cách lấy trung bình các xác suất dự đoán của mỗi bộ trọng số.
Đầu tiên, hãy viết một hàm mà đối với một tập các tham số nhất định sẽ tạo ra các xác suất trên mỗi lớp. Chúng ta có thể sử dụng dist.sample_distributions để có được phân phối chính thức trong mô hình.
def classifier_probs(params):
dists, _ = dist.sample_distributions(seed=random.PRNGKey(0),
value=params + (None,))
return dists[-1].distribution.probs_parameter()
Chúng ta có thể vmap(classifier_probs) trên tập mẫu để có được các xác suất lớp dự đoán cho mỗi mẫu của chúng tôi. Sau đó, chúng tôi tính toán độ chính xác trung bình trên từng mẫu và độ chính xác từ mô hình Bayes được tính trung bình.
all_probs = jit(vmap(classifier_probs))(states)
print('Average accuracy:', jnp.mean(all_probs.argmax(axis=-1) == labels))
print('BMA accuracy:', jnp.mean(all_probs.mean(axis=0).argmax(axis=-1) == labels))
Average accuracy: 0.96952 BMA accuracy: 0.97999996
Có vẻ như BMA giảm tỷ lệ lỗi của chúng tôi xuống gần một phần ba!
Các nguyên tắc cơ bản
TFP trên JAX có một API giống với TF nơi thay vì chấp nhận đối tượng TF như tf.Tensor là nó chấp nhận tương tự JAX. Ví dụ, bất cứ nơi nào một tf.Tensor trước đây được sử dụng như đầu vào, API bây giờ mong muốn một JAX DeviceArray . Thay vì trả lại một tf.Tensor , phương pháp TFP sẽ trở lại DeviceArray s. TFP trên JAX cũng làm việc với các cấu trúc lồng nhau của các đối tượng JAX, giống như một danh sách hoặc từ điển của DeviceArray s.
Phân phối
Hầu hết các bản phân phối của TFP được hỗ trợ trong JAX với ngữ nghĩa rất giống với các bản phân phối TF của chúng. Họ cũng được đăng ký như JAX Pytrees , vì vậy họ có thể đầu vào và đầu ra của chức năng JAX-chuyển.
Các bản phân phối cơ bản
Các log_prob phương pháp để phân phối hoạt động tương tự.
dist = tfd.Normal(0., 1.)
print(dist.log_prob(0.))
-0.9189385
Lấy mẫu từ một phân phối đòi hỏi một cách rõ ràng thông qua trong một PRNGKey (hoặc danh sách các số nguyên) là seed tranh cãi từ khóa. Không chuyển một cách rõ ràng một hạt giống sẽ gây ra lỗi.
tfd.Normal(0., 1.).sample(seed=random.PRNGKey(0))
DeviceArray(-0.20584226, dtype=float32)
Ngữ nghĩa hình dạng cho phân phối vẫn như cũ trong JAX, nơi phân phối mỗi người sẽ có một event_shape và batch_shape và vẽ nhiều mẫu sẽ bổ sung thêm sample_shape chiều.
Ví dụ, một tfd.MultivariateNormalDiag với các thông số vector sẽ có một hình dạng sự kiện vector và hình dạng hàng loạt sản phẩm nào.
dist = tfd.MultivariateNormalDiag(
loc=jnp.zeros(5),
scale_diag=jnp.ones(5)
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: (5,) Batch shape: ()
Mặt khác, một tfd.Normal tham số với vectơ sẽ có một hình dạng sự kiện và hàng loạt vector hình dạng vô hướng.
dist = tfd.Normal(
loc=jnp.ones(5),
scale=jnp.ones(5),
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: () Batch shape: (5,)
Ngữ nghĩa của việc log_prob mẫu hoạt động tương tự trong JAX quá.
dist = tfd.Normal(jnp.zeros(5), jnp.ones(5))
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
dist = tfd.Independent(tfd.Normal(jnp.zeros(5), jnp.ones(5)), 1)
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
(10, 2, 5) (10, 2)
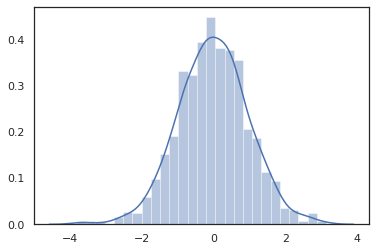
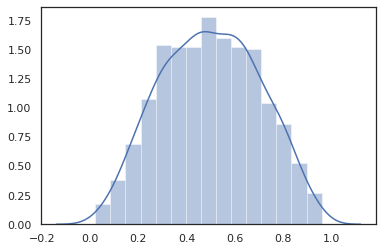
Bởi vì JAX DeviceArray s tương thích với các thư viện như NumPy và Matplotlib, chúng ta có thể nuôi sống mẫu trực tiếp vào một chức năng âm mưu.
sns.distplot(tfd.Normal(0., 1.).sample(1000, seed=random.PRNGKey(0)))
plt.show()
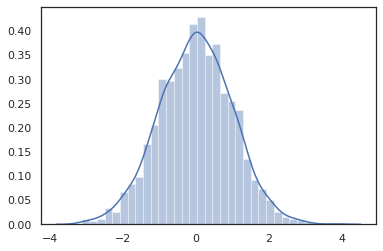
Distribution các phương pháp phù hợp với biến đổi JAX.
sns.distplot(jit(vmap(lambda key: tfd.Normal(0., 1.).sample(seed=key)))(
random.split(random.PRNGKey(0), 2000)))
plt.show()
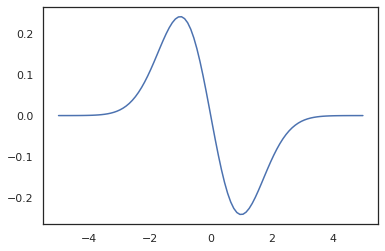
x = jnp.linspace(-5., 5., 100)
plt.plot(x, jit(vmap(grad(tfd.Normal(0., 1.).prob)))(x))
plt.show()
Bởi vì các bản phân phối TFP được đăng ký như các nút pytree JAX, chúng ta có thể viết các chức năng với các bản phân phối như đầu vào hoặc đầu ra và chuyển đổi chúng bằng cách sử jit , nhưng họ chưa được hỗ trợ như các đối số để vmap chức năng -ed.
@jit
def random_distribution(key):
loc_key, scale_key = random.split(key)
loc, log_scale = random.normal(loc_key), random.normal(scale_key)
return tfd.Normal(loc, jnp.exp(log_scale))
random_dist = random_distribution(random.PRNGKey(0))
print(random_dist.mean(), random_dist.variance())
0.14389051 0.081832744
Các bản phân phối đã chuyển đổi
Phân phối biến đổi tức là phân phối có mẫu được chuyển qua một Bijector cũng làm việc ra khỏi hộp (bijectors làm việc quá! Xem dưới đây).
dist = tfd.TransformedDistribution(
tfd.Normal(0., 1.),
tfb.Sigmoid()
)
sns.distplot(dist.sample(1000, seed=random.PRNGKey(0)))
plt.show()
Phân phối chung
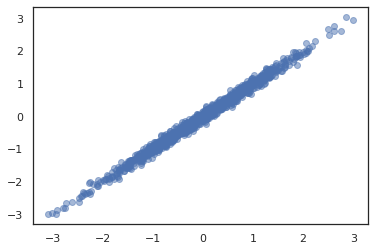
TFP cung cấp JointDistribution s để cho phép kết hợp các bản phân phối thành phần vào một phân phối duy nhất trên nhiều biến ngẫu nhiên. Hiện nay, TFP Mời ba biến thể lõi ( JointDistributionSequential , JointDistributionNamed , và JointDistributionCoroutine ) tất cả đều được hỗ trợ trong JAX. Các AutoBatched biến thể cũng đều được hỗ trợ.
dist = tfd.JointDistributionSequential([
tfd.Normal(0., 1.),
lambda x: tfd.Normal(x, 1e-1)
])
plt.scatter(*dist.sample(1000, seed=random.PRNGKey(0)), alpha=0.5)
plt.show()
joint = tfd.JointDistributionNamed(dict(
e= tfd.Exponential(rate=1.),
n= tfd.Normal(loc=0., scale=2.),
m=lambda n, e: tfd.Normal(loc=n, scale=e),
x=lambda m: tfd.Sample(tfd.Bernoulli(logits=m), 12),
))
joint.sample(seed=random.PRNGKey(0))
{'e': DeviceArray(3.376818, dtype=float32),
'm': DeviceArray(2.5449684, dtype=float32),
'n': DeviceArray(-0.6027825, dtype=float32),
'x': DeviceArray([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int32)}
Root = tfd.JointDistributionCoroutine.Root
def model():
e = yield Root(tfd.Exponential(rate=1.))
n = yield Root(tfd.Normal(loc=0, scale=2.))
m = yield tfd.Normal(loc=n, scale=e)
x = yield tfd.Sample(tfd.Bernoulli(logits=m), 12)
joint = tfd.JointDistributionCoroutine(model)
joint.sample(seed=random.PRNGKey(0))
StructTuple(var0=DeviceArray(0.17315261, dtype=float32), var1=DeviceArray(-3.290489, dtype=float32), var2=DeviceArray(-3.1949058, dtype=float32), var3=DeviceArray([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], dtype=int32))
Các bản phân phối khác
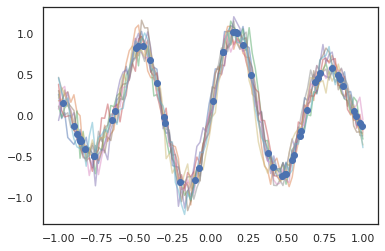
Các quy trình Gaussian cũng hoạt động ở chế độ JAX!
k1, k2, k3 = random.split(random.PRNGKey(0), 3)
observation_noise_variance = 0.01
f = lambda x: jnp.sin(10*x[..., 0]) * jnp.exp(-x[..., 0]**2)
observation_index_points = random.uniform(
k1, [50], minval=-1.,maxval= 1.)[..., jnp.newaxis]
observations = f(observation_index_points) + tfd.Normal(
loc=0., scale=jnp.sqrt(observation_noise_variance)).sample(seed=k2)
index_points = jnp.linspace(-1., 1., 100)[..., jnp.newaxis]
kernel = tfpk.ExponentiatedQuadratic(length_scale=0.1)
gprm = tfd.GaussianProcessRegressionModel(
kernel=kernel,
index_points=index_points,
observation_index_points=observation_index_points,
observations=observations,
observation_noise_variance=observation_noise_variance)
samples = gprm.sample(10, seed=k3)
for i in range(10):
plt.plot(index_points, samples[i], alpha=0.5)
plt.plot(observation_index_points, observations, marker='o', linestyle='')
plt.show()
Các mô hình Markov ẩn cũng được hỗ trợ.
initial_distribution = tfd.Categorical(probs=[0.8, 0.2])
transition_distribution = tfd.Categorical(probs=[[0.7, 0.3],
[0.2, 0.8]])
observation_distribution = tfd.Normal(loc=[0., 15.], scale=[5., 10.])
model = tfd.HiddenMarkovModel(
initial_distribution=initial_distribution,
transition_distribution=transition_distribution,
observation_distribution=observation_distribution,
num_steps=7)
print(model.mean())
print(model.log_prob(jnp.zeros(7)))
print(model.sample(seed=random.PRNGKey(0)))
[3. 6. 7.5 8.249999 8.625001 8.812501 8.90625 ] /usr/local/lib/python3.6/dist-packages/tensorflow_probability/substrates/jax/distributions/hidden_markov_model.py:483: UserWarning: HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug in which the transition model was applied prior to the initial step. This bug has been fixed. You may observe a slight change in behavior. 'HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug ' -19.855635 [ 1.3641367 0.505798 1.3626463 3.6541772 2.272286 15.10309 22.794212 ]
Một vài phân phối như PixelCNN chưa được hỗ trợ do phụ thuộc chặt chẽ vào TensorFlow hoặc XLA không tương thích.
Bijector
Hầu hết các bijector của TFP đều được hỗ trợ trong JAX ngày nay!
tfb.Exp().inverse(1.)
DeviceArray(0., dtype=float32)
bij = tfb.Shift(1.)(tfb.Scale(3.))
print(bij.forward(jnp.ones(5)))
print(bij.inverse(jnp.ones(5)))
[4. 4. 4. 4. 4.] [0. 0. 0. 0. 0.]
b = tfb.FillScaleTriL(diag_bijector=tfb.Exp(), diag_shift=None)
print(b.forward(x=[0., 0., 0.]))
print(b.inverse(y=[[1., 0], [.5, 2]]))
[[1. 0.] [0. 1.]] [0.6931472 0.5 0. ]
b = tfb.Chain([tfb.Exp(), tfb.Softplus()])
# or:
# b = tfb.Exp()(tfb.Softplus())
print(b.forward(-jnp.ones(5)))
[1.3678794 1.3678794 1.3678794 1.3678794 1.3678794]
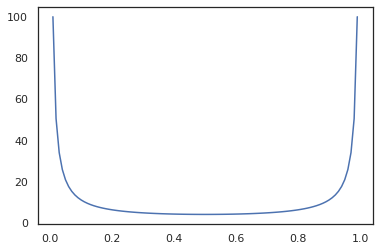
Bijectors tương thích với biến đổi JAX như jit , grad và vmap .
jit(vmap(tfb.Exp().inverse))(jnp.arange(4.))
DeviceArray([ -inf, 0. , 0.6931472, 1.0986123], dtype=float32)
x = jnp.linspace(0., 1., 100)
plt.plot(x, jit(grad(lambda x: vmap(tfb.Sigmoid().inverse)(x).sum()))(x))
plt.show()
Một số bijectors, như RealNVP và FFJORD chưa được hỗ trợ.
MCMC
Chúng tôi đã được chuyển tfp.mcmc để JAX là tốt, vì vậy chúng tôi có thể chạy các thuật toán như Hamiltonian Monte Carlo (HMC) và No-U-Turn-Sampler (NUTS) trong JAX.
target_log_prob = tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)).log_prob
Không giống như TFP vào TF, chúng tôi được yêu cầu phải vượt qua một PRNGKey vào sample_chain sử dụng seed tranh cãi từ khóa.
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-1)
return tfp.mcmc.sample_chain(1000,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
seed=key)
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros(2))
plt.figure()
plt.scatter(*states.T, alpha=0.5)
plt.figure()
plt.plot(log_probs)
plt.show()
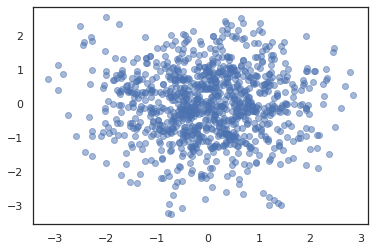
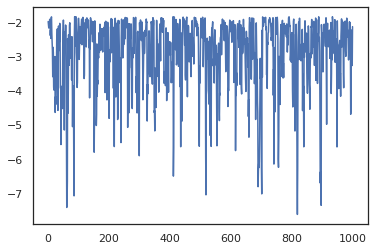
Để chạy nhiều dây chuyền, chúng ta hoặc có thể vượt qua một loạt các quốc gia thành sample_chain hoặc sử dụng vmap (mặc dù chúng ta chưa khám phá sự khác biệt hiệu suất giữa hai cách tiếp cận).
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros([10, 2]))
plt.figure()
for i in range(10):
plt.scatter(*states[:, i].T, alpha=0.5)
plt.figure()
for i in range(10):
plt.plot(log_probs[:, i], alpha=0.5)
plt.show()
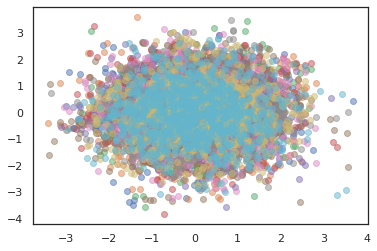
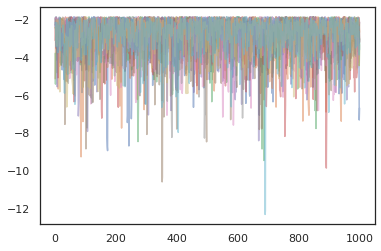
Trình tối ưu hóa
TFP trên JAX hỗ trợ một số trình tối ưu hóa quan trọng như BFGS và L-BFGS. Hãy thiết lập một hàm suy hao bậc hai được chia tỷ lệ đơn giản.
minimum = jnp.array([1.0, 1.0]) # The center of the quadratic bowl.
scales = jnp.array([2.0, 3.0]) # The scales along the two axes.
# The objective function and the gradient.
def quadratic_loss(x):
return jnp.sum(scales * jnp.square(x - minimum))
start = jnp.array([0.6, 0.8]) # Starting point for the search.
BFGS có thể tìm ra mức tối thiểu của khoản lỗ này.
optim_results = tfp.optimizer.bfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
L-BFGS cũng vậy.
optim_results = tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
Để vmap L-BFGS, chúng ta hãy thiết lập của một chức năng tối ưu hóa sự mất mát cho một điểm khởi đầu duy nhất.
def optimize_single(start):
return tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
all_results = jit(vmap(optimize_single))(
random.normal(random.PRNGKey(0), (10, 2)))
assert all(all_results.converged)
for i in range(10):
np.testing.assert_allclose(optim_results.position[i], minimum)
print("Function evaluations: %s" % all_results.num_objective_evaluations)
Function evaluations: [6 6 9 6 6 8 6 8 5 9]
Cảnh báo
Có một số khác biệt cơ bản giữa TF và JAX, một số hành vi TFP sẽ khác nhau giữa hai chất nền và không phải tất cả chức năng đều được hỗ trợ. Ví dụ,
- TFP trên JAX không hỗ trợ bất cứ điều gì như
tf.Variablevì không có gì giống như nó tồn tại trong JAX. Điều này cũng có nghĩa là các tiện ích nhưtfp.util.TransformedVariablekhông được hỗ trợ một trong hai. -
tfp.layerskhông được hỗ trợ trong backend nào, do sự phụ thuộc vào Keras vàtf.Variables. -
tfp.math.minimizekhông làm việc trong TFP trên JAX vì sự phụ thuộc vàotf.Variable. - Với TFP trên JAX, các hình dạng tensor luôn là các giá trị nguyên cụ thể và không bao giờ không xác định / động như trong TFP trên TF.
- Pseudorandomness được xử lý khác nhau trong TF và JAX (xem phụ lục).
- Libraries trong
tfp.experimentalkhông đảm bảo tồn tại trong chất nền JAX. - Quy tắc thăng hạng loại khác nhau giữa TF và JAX. TFP trên JAX cố gắng tôn trọng ngữ nghĩa dtype của TF trong nội bộ, để có tính nhất quán.
- Bijector vẫn chưa được đăng ký là JAX pytrees.
Để xem danh sách đầy đủ về những gì đang được hỗ trợ trong TFP trên JAX, xin vui lòng tham khảo các tài liệu API .
Sự kết luận
Chúng tôi đã chuyển rất nhiều tính năng của TFP sang JAX và rất vui mừng được biết mọi người sẽ xây dựng những gì. Một số chức năng chưa được hỗ trợ; nếu chúng ta đã bỏ lỡ một cái gì đó quan trọng với bạn (hoặc nếu bạn tìm thấy một lỗi!) hãy liên hệ với chúng tôi - bạn có thể gửi email cho tfprobability@tensorflow.org hoặc nộp một vấn đề trên repo Github của chúng tôi .
Phụ lục: hiện tượng giả trong JAX
Hệ số giả ngẫu nhiên (PRNG) mô hình JAX là quốc tịch. Không giống như mô hình trạng thái, không có trạng thái toàn cục có thể thay đổi được mà sẽ phát triển sau mỗi lần rút thăm ngẫu nhiên. Trong mô hình JAX, chúng ta bắt đầu với một chìa khóa PRNG, có tác dụng như một cặp số nguyên 32-bit. Chúng tôi có thể xây dựng các phím này bằng cách sử dụng jax.random.PRNGKey .
key = random.PRNGKey(0) # Creates a key with value [0, 0]
print(key)
[0 0]
Chức năng ngẫu nhiên trong JAX tiêu thụ một chìa khóa để deterministically sản xuất một biến ngẫu nhiên, có nghĩa là họ không nên được sử dụng một lần nữa. Ví dụ, chúng ta có thể sử dụng key để lấy mẫu một giá trị phân phối bình thường, nhưng chúng ta không nên sử dụng key lại ở nơi khác. Hơn nữa, đi qua cùng một giá trị vào random.normal sẽ sản xuất cùng giá trị.
print(random.normal(key))
-0.20584226
Vậy làm thế nào để chúng ta có thể vẽ nhiều mẫu từ một phím duy nhất? Câu trả lời là tách quan trọng. Ý tưởng cơ bản là chúng ta có thể chia nhỏ một PRNGKey thành nhiều, và mỗi người trong số các phím mới có thể được coi là một nguồn độc lập của tính ngẫu nhiên.
key1, key2 = random.split(key, num=2)
print(key1, key2)
[4146024105 967050713] [2718843009 1272950319]
Việc tách khóa là xác định nhưng hỗn loạn, vì vậy mỗi khóa mới bây giờ có thể được sử dụng để vẽ một mẫu ngẫu nhiên riêng biệt.
print(random.normal(key1), random.normal(key2))
0.14389051 -1.2515389
Để biết thêm chi tiết về mô hình chủ chốt tách xác định JAX, xem hướng dẫn này .
