 TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
TensorFlow Olasılık (TFP) şimdi de çalışır olasılık muhakeme ve istatistiksel analizi için bir kütüphane JAX ! Aşina olmayanlar için JAX, birleştirilebilir fonksiyon dönüşümlerine dayalı hızlandırılmış sayısal hesaplama için bir kitaplıktır.
JAX üzerindeki TFP, birçok TFP kullanıcısının artık rahat olduğu soyutlamaları ve API'leri korurken, normal TFP'nin en kullanışlı işlevlerinin çoğunu destekler.
Kurmak
JAX TFP TensorFlow bağlı değildir; TensorFlow'u bu Colab'den tamamen kaldıralım.
pip uninstall tensorflow -y -q
TFP'yi en son gecelik TFP derlemeleriyle JAX'a kurabiliriz.
pip install -Uq tfp-nightly[jax] > /dev/null
Bazı yararlı Python kitaplıklarını içe aktaralım.
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn import datasets
sns.set(style='white')
/usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead. import pandas.util.testing as tm
Ayrıca bazı temel JAX işlevlerini de içe aktaralım.
import jax.numpy as jnp
from jax import grad
from jax import jit
from jax import random
from jax import value_and_grad
from jax import vmap
JAX'ta TFP'yi içe aktarma
JAX üzerinde PFP'yi kullanmak için, ithal jax "substrat" ve genellikle olurdu olarak kullanmak tfp :
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
tfpk = tfp.math.psd_kernels
Demo: Bayes lojistik regresyon
JAX arka ucuyla neler yapabileceğimizi göstermek için klasik Iris veri kümesine uygulanan Bayes lojistik regresyonunu uygulayacağız.
İlk olarak, Iris veri setini içe aktaralım ve bazı meta verileri çıkaralım.
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
Biz kullanarak modeli tanımlayabilirsiniz tfd.JointDistributionCoroutine . Sonra bir yazma ağırlıkları ve önyargı vadede hem standart normal sabıkası koyacağım target_log_prob fonksiyonunu bu pimleri verilerine örneklenmiş etiketleri.
Root = tfd.JointDistributionCoroutine.Root
def model():
w = yield Root(tfd.Sample(tfd.Normal(0., 1.),
sample_shape=(num_features, num_classes)))
b = yield Root(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(num_classes,)))
logits = jnp.dot(features, w) + b
yield tfd.Independent(tfd.Categorical(logits=logits),
reinterpreted_batch_ndims=1)
dist = tfd.JointDistributionCoroutine(model)
def target_log_prob(*params):
return dist.log_prob(params + (labels,))
Bu örnek dist MCMC için bir başlangıç durumunu meydana getirmek için. Daha sonra rastgele bir anahtar ve bir başlangıç durumu alan ve U-Dönüşsüz Örnekleyiciden (NUTS) 500 örnek üreten bir fonksiyon tanımlayabiliriz. Biz gibi JAX dönüşümleri kullanabileceği Not jit XLA kullanarak SOMUNLAR Örnekleyiciyi derlemek için.
init_key, sample_key = random.split(random.PRNGKey(0))
init_params = tuple(dist.sample(seed=init_key)[:-1])
@jit
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-3)
return tfp.mcmc.sample_chain(500,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
num_burnin_steps=500,
seed=key)
states, log_probs = run_chain(sample_key, init_params)
plt.figure()
plt.plot(log_probs)
plt.ylabel('Target Log Prob')
plt.xlabel('Iterations of NUTS')
plt.show()
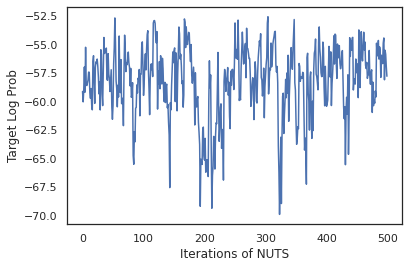
Her bir ağırlık kümesinin tahmin edilen olasılıklarının ortalamasını alarak Bayes modeli ortalamasını (BMA) gerçekleştirmek için örneklerimizi kullanalım.
İlk önce, verilen bir parametre seti için her bir sınıf üzerindeki olasılıkları üretecek bir fonksiyon yazalım. Biz kullanabilirsiniz dist.sample_distributions modelinde nihai dağılımı elde etmek.
def classifier_probs(params):
dists, _ = dist.sample_distributions(seed=random.PRNGKey(0),
value=params + (None,))
return dists[-1].distribution.probs_parameter()
Biz yapabilirsiniz vmap(classifier_probs) bizim numunelerin her biri için tahmini sınıf olasılıklarını almak için numunelerin grubunun üzerine getirin. Daha sonra her örnekteki ortalama doğruluğu ve Bayes modeli ortalamasından gelen doğruluğu hesaplarız.
all_probs = jit(vmap(classifier_probs))(states)
print('Average accuracy:', jnp.mean(all_probs.argmax(axis=-1) == labels))
print('BMA accuracy:', jnp.mean(all_probs.mean(axis=0).argmax(axis=-1) == labels))
Average accuracy: 0.96952 BMA accuracy: 0.97999996
Görünüşe göre BMA hata oranımızı neredeyse üçte bir oranında azaltıyor!
temel bilgiler
JAX TFP yerine TF nesneleri kabul gibi TF özdeş API olan tf.Tensor Jax analog kabul s. Örneğin, bir yerde tf.Tensor önce giriş olarak kullanılan, API artık JAX bekler DeviceArray . Bunun yerine bir geri dönme tf.Tensor , TFP yöntemleri dönecektir DeviceArray s. JAX TFP da bir liste veya sözlük gibi JAX nesnelerin iç içe yapılar ile çalışır DeviceArray s.
dağıtımlar
TFP'nin dağıtımlarının çoğu, JAX'ta TF karşılıklarına çok benzer semantiklerle desteklenir. Ayrıca olarak kayıtlı JAX Pytrees bunlar JAX-transforme edilmiş fonksiyonlar girişler ve çıkışlar olabilmektedir, böylece.
Temel dağıtımlar
log_prob dağılımları yöntemi aynı şekilde çalışır.
dist = tfd.Normal(0., 1.)
print(dist.log_prob(0.))
-0.9189385
Bir dağıtımdan örnekleme açıkça geçen gerektirir PRNGKey olarak (veya tamsayılar listesi) seed anahtar kelime argüman. Bir tohumu açıkça iletmemek bir hata verecektir.
tfd.Normal(0., 1.).sample(seed=random.PRNGKey(0))
DeviceArray(-0.20584226, dtype=float32)
Dağılımları için şekil semantik dağılımları her biri bir olacaktır JAX, aynı kalan event_shape ve batch_shape ilave katacak ve çizim birçok örnekleri sample_shape boyutları.
Örneğin, bir tfd.MultivariateNormalDiag vektör parametrelerle bir vektör olay şekli ve boş toplu bir şekle sahip olacaktır.
dist = tfd.MultivariateNormalDiag(
loc=jnp.zeros(5),
scale_diag=jnp.ones(5)
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: (5,) Batch shape: ()
Öte yandan, bir tfd.Normal bir skaler olay şekli ve vektör toplu bir şekle sahip olacak vektörler ile parametreli.
dist = tfd.Normal(
loc=jnp.ones(5),
scale=jnp.ones(5),
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: () Batch shape: (5,)
Alma semantik log_prob örneklerinin çok JAX 'aynı şekilde çalışır.
dist = tfd.Normal(jnp.zeros(5), jnp.ones(5))
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
dist = tfd.Independent(tfd.Normal(jnp.zeros(5), jnp.ones(5)), 1)
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
(10, 2, 5) (10, 2)
JAX Çünkü DeviceArray ler numpy ve Matplotlib gibi kütüphaneler ile uyumlu, bir komplo fonksiyonu doğrudan örnekleri besleyebilir.
sns.distplot(tfd.Normal(0., 1.).sample(1000, seed=random.PRNGKey(0)))
plt.show()
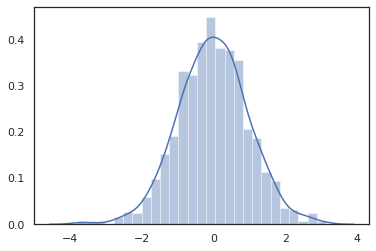
Distribution yöntemleri JAX dönüşümler ile uyumludur.
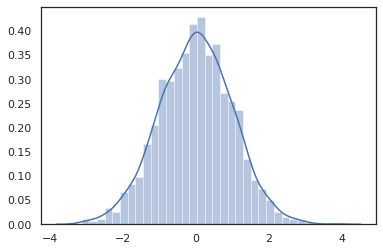
sns.distplot(jit(vmap(lambda key: tfd.Normal(0., 1.).sample(seed=key)))(
random.split(random.PRNGKey(0), 2000)))
plt.show()
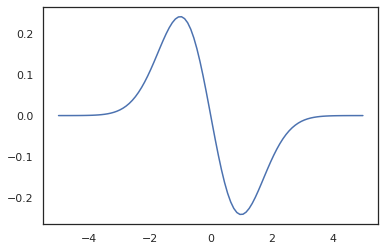
x = jnp.linspace(-5., 5., 100)
plt.plot(x, jit(vmap(grad(tfd.Normal(0., 1.).prob)))(x))
plt.show()
TFP dağılımları JAX pytree düğümler olarak tescil olduğundan, biz giriş veya çıkış olarak dağılımları fonksiyonları yazmak ve kullanarak bunları dönüştürebilir jit , ama henüz argümanlar olarak desteklenmez vmap -ed işlevleri.
@jit
def random_distribution(key):
loc_key, scale_key = random.split(key)
loc, log_scale = random.normal(loc_key), random.normal(scale_key)
return tfd.Normal(loc, jnp.exp(log_scale))
random_dist = random_distribution(random.PRNGKey(0))
print(random_dist.mean(), random_dist.variance())
0.14389051 0.081832744
Dönüştürülmüş dağılımlar
Dönüştürülen dağılımlar olan örnekleri geçirilir dağılımları yani Bijector da kutunun dışında çalışmak (bijectors çok çalışmak! Aşağıya bakınız).
dist = tfd.TransformedDistribution(
tfd.Normal(0., 1.),
tfb.Sigmoid()
)
sns.distplot(dist.sample(1000, seed=random.PRNGKey(0)))
plt.show()
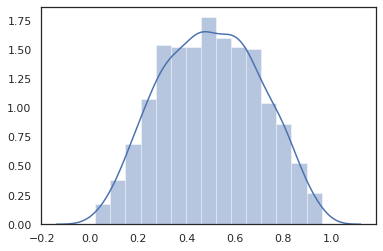
Ortak dağıtımlar
TFP sunmaktadır JointDistribution s çoklu rastlantı değişkenler üzerindeki tek bir dağılım halinde bileşen dağılımları kombine sağlamaktır. Şu anda, TFP teklifler üç temel varyantları ( JointDistributionSequential , JointDistributionNamed ve JointDistributionCoroutine ) hepsi jax desteklenir. AutoBatched varyantları aynı zamanda tüm desteklenmektedir.
dist = tfd.JointDistributionSequential([
tfd.Normal(0., 1.),
lambda x: tfd.Normal(x, 1e-1)
])
plt.scatter(*dist.sample(1000, seed=random.PRNGKey(0)), alpha=0.5)
plt.show()
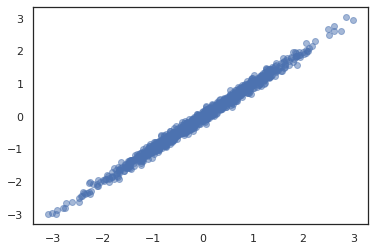
joint = tfd.JointDistributionNamed(dict(
e= tfd.Exponential(rate=1.),
n= tfd.Normal(loc=0., scale=2.),
m=lambda n, e: tfd.Normal(loc=n, scale=e),
x=lambda m: tfd.Sample(tfd.Bernoulli(logits=m), 12),
))
joint.sample(seed=random.PRNGKey(0))
{'e': DeviceArray(3.376818, dtype=float32),
'm': DeviceArray(2.5449684, dtype=float32),
'n': DeviceArray(-0.6027825, dtype=float32),
'x': DeviceArray([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int32)}
Root = tfd.JointDistributionCoroutine.Root
def model():
e = yield Root(tfd.Exponential(rate=1.))
n = yield Root(tfd.Normal(loc=0, scale=2.))
m = yield tfd.Normal(loc=n, scale=e)
x = yield tfd.Sample(tfd.Bernoulli(logits=m), 12)
joint = tfd.JointDistributionCoroutine(model)
joint.sample(seed=random.PRNGKey(0))
StructTuple(var0=DeviceArray(0.17315261, dtype=float32), var1=DeviceArray(-3.290489, dtype=float32), var2=DeviceArray(-3.1949058, dtype=float32), var3=DeviceArray([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], dtype=int32))
Diğer dağıtımlar
Gauss süreçleri JAX modunda da çalışır!
k1, k2, k3 = random.split(random.PRNGKey(0), 3)
observation_noise_variance = 0.01
f = lambda x: jnp.sin(10*x[..., 0]) * jnp.exp(-x[..., 0]**2)
observation_index_points = random.uniform(
k1, [50], minval=-1.,maxval= 1.)[..., jnp.newaxis]
observations = f(observation_index_points) + tfd.Normal(
loc=0., scale=jnp.sqrt(observation_noise_variance)).sample(seed=k2)
index_points = jnp.linspace(-1., 1., 100)[..., jnp.newaxis]
kernel = tfpk.ExponentiatedQuadratic(length_scale=0.1)
gprm = tfd.GaussianProcessRegressionModel(
kernel=kernel,
index_points=index_points,
observation_index_points=observation_index_points,
observations=observations,
observation_noise_variance=observation_noise_variance)
samples = gprm.sample(10, seed=k3)
for i in range(10):
plt.plot(index_points, samples[i], alpha=0.5)
plt.plot(observation_index_points, observations, marker='o', linestyle='')
plt.show()
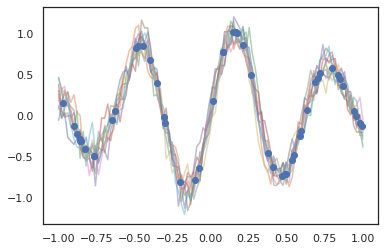
Gizli Markov modelleri de desteklenmektedir.
initial_distribution = tfd.Categorical(probs=[0.8, 0.2])
transition_distribution = tfd.Categorical(probs=[[0.7, 0.3],
[0.2, 0.8]])
observation_distribution = tfd.Normal(loc=[0., 15.], scale=[5., 10.])
model = tfd.HiddenMarkovModel(
initial_distribution=initial_distribution,
transition_distribution=transition_distribution,
observation_distribution=observation_distribution,
num_steps=7)
print(model.mean())
print(model.log_prob(jnp.zeros(7)))
print(model.sample(seed=random.PRNGKey(0)))
[3. 6. 7.5 8.249999 8.625001 8.812501 8.90625 ] /usr/local/lib/python3.6/dist-packages/tensorflow_probability/substrates/jax/distributions/hidden_markov_model.py:483: UserWarning: HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug in which the transition model was applied prior to the initial step. This bug has been fixed. You may observe a slight change in behavior. 'HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug ' -19.855635 [ 1.3641367 0.505798 1.3626463 3.6541772 2.272286 15.10309 22.794212 ]
Gibi birkaç dağılımlar PixelCNN nedeniyle TensorFlow veya XLA uyumsuzlukları sıkı bağımlılıkları henüz desteklenmemektedir.
Bijektörler
TFP'nin çoğu bijektörü bugün JAX'ta destekleniyor!
tfb.Exp().inverse(1.)
DeviceArray(0., dtype=float32)
bij = tfb.Shift(1.)(tfb.Scale(3.))
print(bij.forward(jnp.ones(5)))
print(bij.inverse(jnp.ones(5)))
[4. 4. 4. 4. 4.] [0. 0. 0. 0. 0.]
b = tfb.FillScaleTriL(diag_bijector=tfb.Exp(), diag_shift=None)
print(b.forward(x=[0., 0., 0.]))
print(b.inverse(y=[[1., 0], [.5, 2]]))
[[1. 0.] [0. 1.]] [0.6931472 0.5 0. ]
b = tfb.Chain([tfb.Exp(), tfb.Softplus()])
# or:
# b = tfb.Exp()(tfb.Softplus())
print(b.forward(-jnp.ones(5)))
[1.3678794 1.3678794 1.3678794 1.3678794 1.3678794]
Bijectors gibi JAX dönüşümleri ile uyumlu jit , grad ve vmap .
jit(vmap(tfb.Exp().inverse))(jnp.arange(4.))
DeviceArray([ -inf, 0. , 0.6931472, 1.0986123], dtype=float32)
x = jnp.linspace(0., 1., 100)
plt.plot(x, jit(grad(lambda x: vmap(tfb.Sigmoid().inverse)(x).sum()))(x))
plt.show()
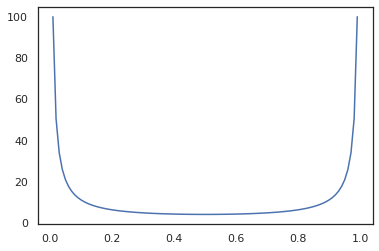
Gibi bazı bijectors, RealNVP ve FFJORD henüz desteklenmemektedir.
MCMC
Biz taşıdık ettik tfp.mcmc biz Hamilton Monte Carlo (HMC) ve JAX '(İBBS) Hayır-U dönüşü-Sampler gibi algoritmalar çalışabilmesi için, hem de jax için.
target_log_prob = tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)).log_prob
TF üzerinde TFP aksine biz bir başarılı olmaları gerekir PRNGKey içine sample_chain kullanarak seed anahtar kelime argüman.
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-1)
return tfp.mcmc.sample_chain(1000,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
seed=key)
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros(2))
plt.figure()
plt.scatter(*states.T, alpha=0.5)
plt.figure()
plt.plot(log_probs)
plt.show()
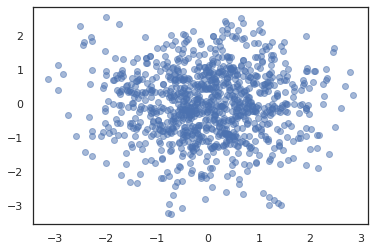
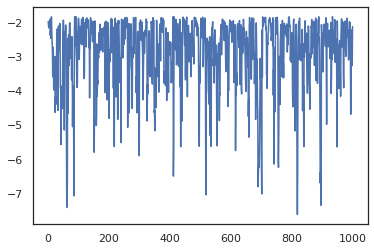
Birden zincirlerini çalıştırmak için, öncelikle içine devletler toplu geçebilir sample_chain veya kullanım vmap (henüz iki yaklaşım arasındaki performans farklılıklarını araştırılmalıdır değil gerçi).
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros([10, 2]))
plt.figure()
for i in range(10):
plt.scatter(*states[:, i].T, alpha=0.5)
plt.figure()
for i in range(10):
plt.plot(log_probs[:, i], alpha=0.5)
plt.show()
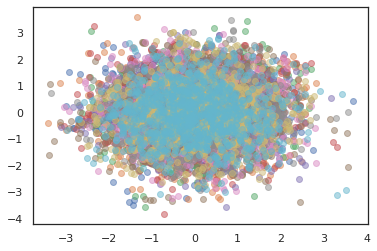
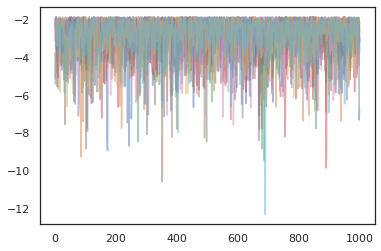
Optimize Ediciler
JAX üzerindeki TFP, BFGS ve L-BFGS gibi bazı önemli optimize edicileri destekler. Basit bir ölçeklendirilmiş ikinci dereceden kayıp fonksiyonu kuralım.
minimum = jnp.array([1.0, 1.0]) # The center of the quadratic bowl.
scales = jnp.array([2.0, 3.0]) # The scales along the two axes.
# The objective function and the gradient.
def quadratic_loss(x):
return jnp.sum(scales * jnp.square(x - minimum))
start = jnp.array([0.6, 0.8]) # Starting point for the search.
BFGS bu kaybın minimumunu bulabilir.
optim_results = tfp.optimizer.bfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
L-BFGS de olabilir.
optim_results = tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
To vmap L-BFGS, tek bir başlangıç noktası için kaybını optimize eden bir fonksiyonu kalmış kümesi olsun.
def optimize_single(start):
return tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
all_results = jit(vmap(optimize_single))(
random.normal(random.PRNGKey(0), (10, 2)))
assert all(all_results.converged)
for i in range(10):
np.testing.assert_allclose(optim_results.position[i], minimum)
print("Function evaluations: %s" % all_results.num_objective_evaluations)
Function evaluations: [6 6 9 6 6 8 6 8 5 9]
uyarılar
TF ve JAX arasında bazı temel farklılıklar vardır, bazı TFP davranışları iki alt tabaka arasında farklı olacaktır ve tüm işlevler desteklenmez. Örneğin,
- JAX TFP böyle bir şey desteklemiyor
tf.Variableo jax var gibi bir şey bu yana. Bu aynı zamanda gibi programları anlamınatfp.util.TransformedVariableya desteklenmez. -
tfp.layersnedeniyle Keras ve bağlı olması, henüz arka uç desteklenmeyentf.Variables. -
tfp.math.minimizenedeniyle ihtiyaç duyduğundan JAX üzerinde TFV işi yapmaztf.Variable. - JAX üzerinde TFP ile, tensör şekilleri her zaman somut tamsayı değerleridir ve asla TF üzerinde TFP'de olduğu gibi bilinmeyen/dinamik değildir.
- Sahte rastgelelik, TF ve JAX'ta farklı şekilde işlenir (bkz. ek).
- Kütüphane
tfp.experimentalJAX substrata mevcut garanti edilmez. - Dtype promosyon kuralları TF ve JAX arasında farklıdır. JAX üzerindeki TFP, tutarlılık için dahili olarak TF'nin dtype semantiğine saygı göstermeye çalışır.
- Bijektörler henüz JAX pytrees olarak kaydedilmedi.
Jax üzerinde TFP desteklenir şeyin tam listesini görmek için, bakınız API belgeleri .
Çözüm
TFP'nin birçok özelliğini JAX'a taşıdık ve herkesin ne inşa edeceğini görmekten heyecan duyuyoruz. Bazı işlevler henüz desteklenmemektedir; Size önemli bir şey kaçırmıştım (veya bir böcek bulursanız!) bize geçin - Eğer e-posta tfprobability@tensorflow.org veya üzerinde bir sorunu dosyasını bizim Github repo .
Ek: JAX'ta sözde rastgelelik
Jax'in Yalancı rasgele sayı nesil (PRNG) modeli vatansız olduğunu. Durum bilgisi olan bir modelden farklı olarak, her rastgele çekilişten sonra gelişen değiştirilebilir bir küresel durum yoktur. Jax'in modelde, biz 32 bit tamsayılar bir çift gibi davranan bir PRNG anahtarı ile başlar. Biz kullanarak bu tuşları oluşturabilirsiniz jax.random.PRNGKey .
key = random.PRNGKey(0) # Creates a key with value [0, 0]
print(key)
[0 0]
Deterministik tekrar kullanılmamalıdır anlamına rastgele değişken üretmek için JAX 'Rastgele fonksiyonlar bir anahtar tüketir. Örneğin, kullanabilirsiniz key normal dağılıma sahip değerini örnek, ama biz kullanmamalısınız key tekrar başka bir yerde. Ayrıca, içine aynı değere geçen random.normal aynı değeri üretir.
print(random.normal(key))
-0.20584226
Peki, tek bir anahtardan birden fazla örneği nasıl çizebiliriz? Cevap anahtarı parçalanması. Temel fikir bir bölebilmeniz PRNGKey multiple ve yeni anahtarların her rastgelelik bağımsız bir kaynak olarak tedavi edilebilir.
key1, key2 = random.split(key, num=2)
print(key1, key2)
[4146024105 967050713] [2718843009 1272950319]
Anahtar bölme deterministiktir ancak kaotiktir, bu nedenle her yeni anahtar artık farklı bir rastgele örnek çizmek için kullanılabilir.
print(random.normal(key1), random.normal(key2))
0.14389051 -1.2515389
Jax'in deterministik anahtar bölme modeli hakkında daha fazla ayrıntı için bkz bu kılavuzu .
