 Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
TensorFlow Probabilidade (TFP) é uma biblioteca para raciocínio probabilístico e análise estatística que agora também funciona em JAX ! Para aqueles que não estão familiarizados, JAX é uma biblioteca para computação numérica acelerada baseada em transformações de funções composíveis.
O TFP no JAX oferece suporte a muitas das funcionalidades mais úteis do TFP regular, preservando as abstrações e APIs com as quais muitos usuários do TFP agora se sentem confortáveis.
Configurar
Não TFP em JAX não dependem TensorFlow; vamos desinstalar o TensorFlow deste Colab inteiramente.
pip uninstall tensorflow -y -q
Podemos instalar o TFP no JAX com as compilações noturnas mais recentes do TFP.
pip install -Uq tfp-nightly[jax] > /dev/null
Vamos importar algumas bibliotecas Python úteis.
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn import datasets
sns.set(style='white')
/usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead. import pandas.util.testing as tm
Vamos também importar algumas funcionalidades básicas do JAX.
import jax.numpy as jnp
from jax import grad
from jax import jit
from jax import random
from jax import value_and_grad
from jax import vmap
Importando TFP em JAX
Para usar TFP em JAX, simplesmente importar o jax "substrato" e usá-lo como você normalmente seria tfp :
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
tfpk = tfp.math.psd_kernels
Demonstração: regressão logística bayesiana
Para demonstrar o que podemos fazer com o back-end JAX, implementaremos a regressão logística Bayesiana aplicada ao conjunto de dados Iris clássico.
Primeiro, vamos importar o conjunto de dados Iris e extrair alguns metadados.
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
Podemos definir o modelo usando tfd.JointDistributionCoroutine . Vamos colocar priores normais padrão em ambos os pesos e o termo viés, em seguida, escrever uma target_log_prob função que pins os rótulos amostradas aos dados.
Root = tfd.JointDistributionCoroutine.Root
def model():
w = yield Root(tfd.Sample(tfd.Normal(0., 1.),
sample_shape=(num_features, num_classes)))
b = yield Root(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(num_classes,)))
logits = jnp.dot(features, w) + b
yield tfd.Independent(tfd.Categorical(logits=logits),
reinterpreted_batch_ndims=1)
dist = tfd.JointDistributionCoroutine(model)
def target_log_prob(*params):
return dist.log_prob(params + (labels,))
Nós amostra de dist para produzir um estado inicial para MCMC. Podemos então definir uma função que recebe uma chave aleatória e um estado inicial e produz 500 amostras de um No-U-Turn-Sampler (NUTS). Note que podemos usar transformações JAX como jit para compilar o nosso amostrador NUTS usando XLA.
init_key, sample_key = random.split(random.PRNGKey(0))
init_params = tuple(dist.sample(seed=init_key)[:-1])
@jit
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-3)
return tfp.mcmc.sample_chain(500,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
num_burnin_steps=500,
seed=key)
states, log_probs = run_chain(sample_key, init_params)
plt.figure()
plt.plot(log_probs)
plt.ylabel('Target Log Prob')
plt.xlabel('Iterations of NUTS')
plt.show()
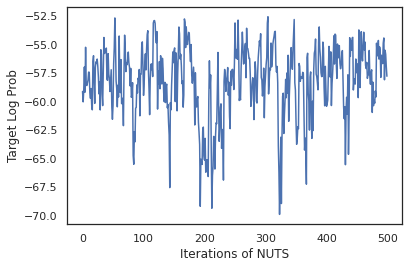
Vamos usar nossas amostras para realizar a média do modelo Bayesiano (BMA), calculando a média das probabilidades previstas de cada conjunto de pesos.
Primeiro, vamos escrever uma função que, para um determinado conjunto de parâmetros, produzirá as probabilidades de cada classe. Podemos usar dist.sample_distributions obter a distribuição final no modelo.
def classifier_probs(params):
dists, _ = dist.sample_distributions(seed=random.PRNGKey(0),
value=params + (None,))
return dists[-1].distribution.probs_parameter()
Podemos vmap(classifier_probs) sobre o conjunto de amostras para obter as probabilidades de classe previstos para cada uma das nossas amostras. Em seguida, calculamos a precisão média em cada amostra e a precisão da média do modelo bayesiano.
all_probs = jit(vmap(classifier_probs))(states)
print('Average accuracy:', jnp.mean(all_probs.argmax(axis=-1) == labels))
print('BMA accuracy:', jnp.mean(all_probs.mean(axis=0).argmax(axis=-1) == labels))
Average accuracy: 0.96952 BMA accuracy: 0.97999996
Parece que o BMA reduz nossa taxa de erro em quase um terço!
Fundamentos
TFP em JAX tem uma API idêntico ao TF, onde em vez de aceitar objetos TF como tf.Tensor é aceita a analógicas JAX. Por exemplo, sempre que uma tf.Tensor foi anteriormente utilizado como entrada, o API agora espera um JAX DeviceArray . Em vez de retornar um tf.Tensor , métodos PTF voltará DeviceArray s. TFP em JAX também trabalha com estruturas aninhadas de objetos JAX, como uma lista ou dicionário de DeviceArray s.
Distribuições
A maioria das distribuições da TFP são suportadas em JAX com semânticas muito semelhantes às suas contrapartes TF. Eles também são registrados como JAX Pytrees , para que possam ser entradas e saídas de funções JAX-transformados.
Distribuições básicas
O log_prob método para distribuições funciona da mesma.
dist = tfd.Normal(0., 1.)
print(dist.log_prob(0.))
-0.9189385
Amostragem de uma distribuição exige explicitamente passando um PRNGKey (ou lista de inteiros) como a seed argumento palavra-chave. Deixar de passar explicitamente uma semente gerará um erro.
tfd.Normal(0., 1.).sample(seed=random.PRNGKey(0))
DeviceArray(-0.20584226, dtype=float32)
A semântica da forma para distribuições permanecer a mesma no JAX, onde as distribuições terão cada uma event_shape e um batch_shape e tiragem muitas amostras irá adicionar adicionais sample_shape dimensões.
Por exemplo, um tfd.MultivariateNormalDiag com parâmetros vector terá uma forma evento vector e forma lote vazio.
dist = tfd.MultivariateNormalDiag(
loc=jnp.zeros(5),
scale_diag=jnp.ones(5)
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: (5,) Batch shape: ()
Por outro lado, um tfd.Normal parametrizado com vectores terão uma forma forma evento e lote vector escalar.
dist = tfd.Normal(
loc=jnp.ones(5),
scale=jnp.ones(5),
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: () Batch shape: (5,)
A semântica de tomar log_prob de amostras funciona da mesma em JAX também.
dist = tfd.Normal(jnp.zeros(5), jnp.ones(5))
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
dist = tfd.Independent(tfd.Normal(jnp.zeros(5), jnp.ones(5)), 1)
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
(10, 2, 5) (10, 2)
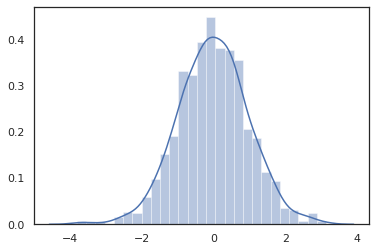
Porque JAX DeviceArray s são compatíveis com bibliotecas como NumPy e Matplotlib, que podem alimentar as amostras directamente em um traçado de funções.
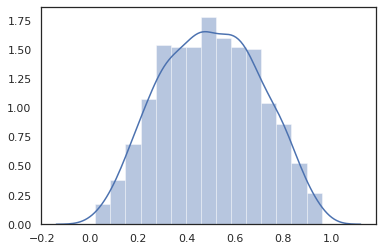
sns.distplot(tfd.Normal(0., 1.).sample(1000, seed=random.PRNGKey(0)))
plt.show()
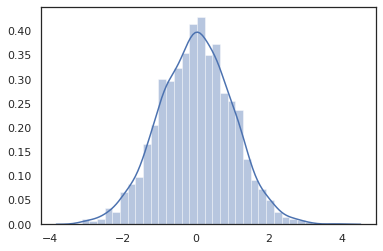
Distribution métodos são compatíveis com transformações JAX.
sns.distplot(jit(vmap(lambda key: tfd.Normal(0., 1.).sample(seed=key)))(
random.split(random.PRNGKey(0), 2000)))
plt.show()
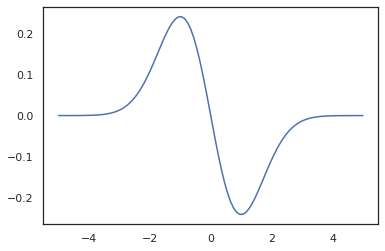
x = jnp.linspace(-5., 5., 100)
plt.plot(x, jit(vmap(grad(tfd.Normal(0., 1.).prob)))(x))
plt.show()
Porque distribuições TFP são registrados como nós pytree JAX, podemos escrever funções com distribuições como entradas ou saídas e transformá-los usando jit , mas eles ainda não são suportados como argumentos para vmap funções ed.
@jit
def random_distribution(key):
loc_key, scale_key = random.split(key)
loc, log_scale = random.normal(loc_key), random.normal(scale_key)
return tfd.Normal(loc, jnp.exp(log_scale))
random_dist = random_distribution(random.PRNGKey(0))
print(random_dist.mean(), random_dist.variance())
0.14389051 0.081832744
Distribuições transformadas
Distribuições transformados ou seja, distribuições cujas amostras são passados através de um Bijector também trabalhar fora da caixa (bijectors trabalhar muito! Veja abaixo).
dist = tfd.TransformedDistribution(
tfd.Normal(0., 1.),
tfb.Sigmoid()
)
sns.distplot(dist.sample(1000, seed=random.PRNGKey(0)))
plt.show()
Distribuições conjuntas
PTF oferece JointDistribution s para permitir a combinação de distribuições de componentes numa única distribuição ao longo de várias variáveis aleatórias. Atualmente, ofertas TFP três variantes principais ( JointDistributionSequential , JointDistributionNamed e JointDistributionCoroutine ) todos os quais são suportados no JAX. Os AutoBatched variantes também são suportados.
dist = tfd.JointDistributionSequential([
tfd.Normal(0., 1.),
lambda x: tfd.Normal(x, 1e-1)
])
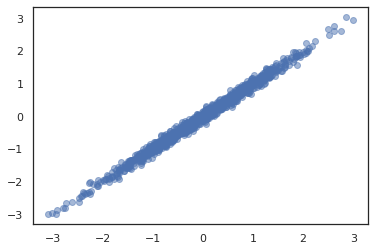
plt.scatter(*dist.sample(1000, seed=random.PRNGKey(0)), alpha=0.5)
plt.show()
joint = tfd.JointDistributionNamed(dict(
e= tfd.Exponential(rate=1.),
n= tfd.Normal(loc=0., scale=2.),
m=lambda n, e: tfd.Normal(loc=n, scale=e),
x=lambda m: tfd.Sample(tfd.Bernoulli(logits=m), 12),
))
joint.sample(seed=random.PRNGKey(0))
{'e': DeviceArray(3.376818, dtype=float32),
'm': DeviceArray(2.5449684, dtype=float32),
'n': DeviceArray(-0.6027825, dtype=float32),
'x': DeviceArray([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int32)}
Root = tfd.JointDistributionCoroutine.Root
def model():
e = yield Root(tfd.Exponential(rate=1.))
n = yield Root(tfd.Normal(loc=0, scale=2.))
m = yield tfd.Normal(loc=n, scale=e)
x = yield tfd.Sample(tfd.Bernoulli(logits=m), 12)
joint = tfd.JointDistributionCoroutine(model)
joint.sample(seed=random.PRNGKey(0))
StructTuple(var0=DeviceArray(0.17315261, dtype=float32), var1=DeviceArray(-3.290489, dtype=float32), var2=DeviceArray(-3.1949058, dtype=float32), var3=DeviceArray([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], dtype=int32))
Outras distribuições
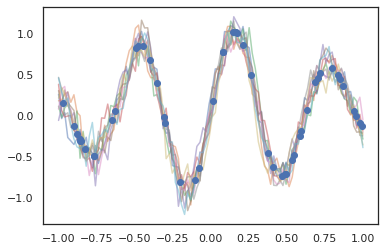
Os processos gaussianos também funcionam no modo JAX!
k1, k2, k3 = random.split(random.PRNGKey(0), 3)
observation_noise_variance = 0.01
f = lambda x: jnp.sin(10*x[..., 0]) * jnp.exp(-x[..., 0]**2)
observation_index_points = random.uniform(
k1, [50], minval=-1.,maxval= 1.)[..., jnp.newaxis]
observations = f(observation_index_points) + tfd.Normal(
loc=0., scale=jnp.sqrt(observation_noise_variance)).sample(seed=k2)
index_points = jnp.linspace(-1., 1., 100)[..., jnp.newaxis]
kernel = tfpk.ExponentiatedQuadratic(length_scale=0.1)
gprm = tfd.GaussianProcessRegressionModel(
kernel=kernel,
index_points=index_points,
observation_index_points=observation_index_points,
observations=observations,
observation_noise_variance=observation_noise_variance)
samples = gprm.sample(10, seed=k3)
for i in range(10):
plt.plot(index_points, samples[i], alpha=0.5)
plt.plot(observation_index_points, observations, marker='o', linestyle='')
plt.show()
Modelos ocultos de Markov também são suportados.
initial_distribution = tfd.Categorical(probs=[0.8, 0.2])
transition_distribution = tfd.Categorical(probs=[[0.7, 0.3],
[0.2, 0.8]])
observation_distribution = tfd.Normal(loc=[0., 15.], scale=[5., 10.])
model = tfd.HiddenMarkovModel(
initial_distribution=initial_distribution,
transition_distribution=transition_distribution,
observation_distribution=observation_distribution,
num_steps=7)
print(model.mean())
print(model.log_prob(jnp.zeros(7)))
print(model.sample(seed=random.PRNGKey(0)))
[3. 6. 7.5 8.249999 8.625001 8.812501 8.90625 ] /usr/local/lib/python3.6/dist-packages/tensorflow_probability/substrates/jax/distributions/hidden_markov_model.py:483: UserWarning: HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug in which the transition model was applied prior to the initial step. This bug has been fixed. You may observe a slight change in behavior. 'HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug ' -19.855635 [ 1.3641367 0.505798 1.3626463 3.6541772 2.272286 15.10309 22.794212 ]
Algumas distribuições como PixelCNN ainda não são suportados, devido a dependências estritas sobre TensorFlow ou XLA incompatibilidades.
Bijetores
A maioria dos bijetores da TFP são suportados no JAX hoje!
tfb.Exp().inverse(1.)
DeviceArray(0., dtype=float32)
bij = tfb.Shift(1.)(tfb.Scale(3.))
print(bij.forward(jnp.ones(5)))
print(bij.inverse(jnp.ones(5)))
[4. 4. 4. 4. 4.] [0. 0. 0. 0. 0.]
b = tfb.FillScaleTriL(diag_bijector=tfb.Exp(), diag_shift=None)
print(b.forward(x=[0., 0., 0.]))
print(b.inverse(y=[[1., 0], [.5, 2]]))
[[1. 0.] [0. 1.]] [0.6931472 0.5 0. ]
b = tfb.Chain([tfb.Exp(), tfb.Softplus()])
# or:
# b = tfb.Exp()(tfb.Softplus())
print(b.forward(-jnp.ones(5)))
[1.3678794 1.3678794 1.3678794 1.3678794 1.3678794]
Bijectors são compatíveis com as transformações JAX como jit , grad e vmap .
jit(vmap(tfb.Exp().inverse))(jnp.arange(4.))
DeviceArray([ -inf, 0. , 0.6931472, 1.0986123], dtype=float32)
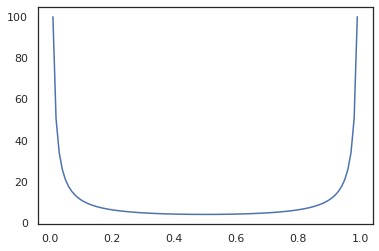
x = jnp.linspace(0., 1., 100)
plt.plot(x, jit(grad(lambda x: vmap(tfb.Sigmoid().inverse)(x).sum()))(x))
plt.show()
Alguns bijectors, como RealNVP e FFJORD ainda não são suportados.
MCMC
Nós temos portado tfp.mcmc para JAX, bem como, para que possamos executar algoritmos como hamiltoniano Monte Carlo (HMC) eo No-U-Turn-Sampler (NUTS) em JAX.
target_log_prob = tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)).log_prob
Ao contrário TFP em TF, somos obrigados a passar por um PRNGKey em sample_chain usando a seed argumento palavra-chave.
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-1)
return tfp.mcmc.sample_chain(1000,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
seed=key)
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros(2))
plt.figure()
plt.scatter(*states.T, alpha=0.5)
plt.figure()
plt.plot(log_probs)
plt.show()
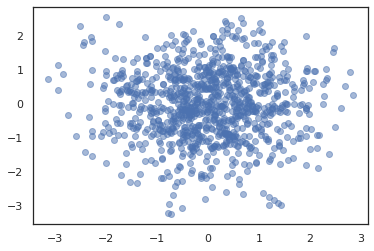
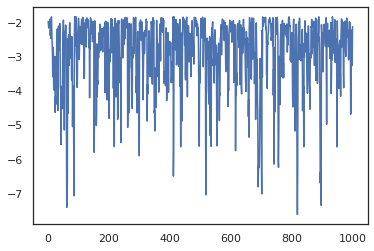
Para executar várias cadeias, que pode passar um lote de estados em sample_chain ou uso vmap (embora ainda não foram exploradas as diferenças de desempenho entre as duas abordagens).
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros([10, 2]))
plt.figure()
for i in range(10):
plt.scatter(*states[:, i].T, alpha=0.5)
plt.figure()
for i in range(10):
plt.plot(log_probs[:, i], alpha=0.5)
plt.show()
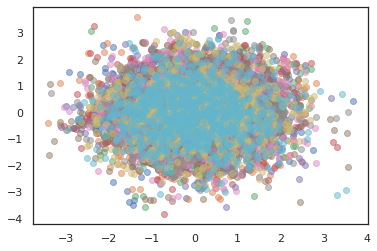
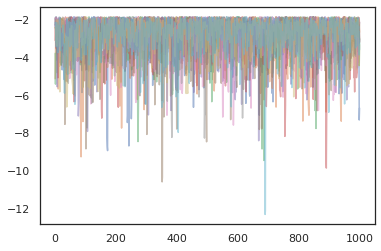
Otimizadores
O TFP no JAX oferece suporte a alguns otimizadores importantes, como BFGS e L-BFGS. Vamos configurar uma função de perda quadrática escalonada simples.
minimum = jnp.array([1.0, 1.0]) # The center of the quadratic bowl.
scales = jnp.array([2.0, 3.0]) # The scales along the two axes.
# The objective function and the gradient.
def quadratic_loss(x):
return jnp.sum(scales * jnp.square(x - minimum))
start = jnp.array([0.6, 0.8]) # Starting point for the search.
O BFGS pode encontrar o mínimo dessa perda.
optim_results = tfp.optimizer.bfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
O mesmo pode acontecer com o L-BFGS.
optim_results = tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
Para vmap L-BFGS, vamos configurar uma função que optimiza a perda de um único ponto de partida.
def optimize_single(start):
return tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
all_results = jit(vmap(optimize_single))(
random.normal(random.PRNGKey(0), (10, 2)))
assert all(all_results.converged)
for i in range(10):
np.testing.assert_allclose(optim_results.position[i], minimum)
print("Function evaluations: %s" % all_results.num_objective_evaluations)
Function evaluations: [6 6 9 6 6 8 6 8 5 9]
Ressalvas
Existem algumas diferenças fundamentais entre TF e JAX, alguns comportamentos de TFP serão diferentes entre os dois substratos e nem todas as funcionalidades são suportadas. Por exemplo,
- Não TFP em JAX não suporta qualquer coisa como
tf.Variablepois nada como ele existe em JAX. Isto também significa utilidades comotfp.util.TransformedVariablenão são suportados quer. -
tfp.layersnão é suportado no backend, no entanto, devido à sua dependência de Keras etf.Variables. -
tfp.math.minimizenão funciona na TFP em JAX por causa de sua dependência detf.Variable. - Com o TFP no JAX, as formas do tensor são sempre valores inteiros concretos e nunca são desconhecidos / dinâmicos como no TFP no TF.
- A pseudo-aleatoriedade é tratada de forma diferente em TF e JAX (consulte o apêndice).
- Bibliotecas em
tfp.experimentalnão são garantidos a existir no substrato JAX. - As regras de promoção Dtype são diferentes entre TF e JAX. O TFP no JAX tenta respeitar a semântica dtype do TF internamente, para consistência.
- Os bijetores ainda não foram registrados como pytrees JAX.
Para ver a lista completa do que é suportado no TFP em JAX, consulte a documentação da API .
Conclusão
Transferimos muitos recursos do TFP para JAX e estamos ansiosos para ver o que todos irão construir. Algumas funcionalidades ainda não são suportadas; se perdemos algo importante para você (ou se você encontrar um erro!), entre em contato conosco - você pode enviar e-mail tfprobability@tensorflow.org ou arquivar um problema em nosso repo Github .
Apêndice: pseudo-aleatoriedade em JAX
O modelo de JAX números pseudo-aleatórios geração (PRNG) é apátrida. Ao contrário de um modelo com estado, não existe um estado global mutável que evolui após cada sorteio aleatório. No modelo de JAX, começamos com uma chave PRNG, que atua como um par de inteiros de 32 bits. Podemos construir essas chaves usando jax.random.PRNGKey .
key = random.PRNGKey(0) # Creates a key with value [0, 0]
print(key)
[0 0]
Funções aleatórias em JAX consumir uma chave para deterministically produzir uma variável aleatória, o que significa que não deve ser utilizado novamente. Por exemplo, podemos usar key para provar um valor distribuído normalmente, mas não devemos usar key de novo em outro lugar. Além disso, passando o mesmo valor em random.normal irá produzir o mesmo valor.
print(random.normal(key))
-0.20584226
Então, como podemos extrair várias amostras de uma única chave? A resposta é divisão de chave. A idéia básica é que podemos dividir um PRNGKey em vários, e cada uma das novas chaves podem ser tratados como uma fonte independente de aleatoriedade.
key1, key2 = random.split(key, num=2)
print(key1, key2)
[4146024105 967050713] [2718843009 1272950319]
A divisão de chave é determinística, mas é caótica, portanto, cada nova chave agora pode ser usada para desenhar uma amostra aleatória distinta.
print(random.normal(key1), random.normal(key2))
0.14389051 -1.2515389
Para mais detalhes sobre modelo de chave de divisão determinista de JAX, consulte este guia .
