 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
TensorFlow Prawdopodobieństwo (TFP) jest biblioteką do probabilistycznego rozumowania i analizy statystycznej, która teraz działa również na JAX ! Dla tych, którzy nie są zaznajomieni, JAX jest biblioteką do przyspieszonych obliczeń numerycznych opartych na transformacjach funkcji komponowalnych.
TFP w JAX obsługuje wiele najbardziej przydatnych funkcji zwykłego TFP, zachowując jednocześnie abstrakcje i interfejsy API, z którymi wielu użytkowników TFP jest teraz zadowolonych.
Ustawiać
TFP na JAX nie zależy TensorFlow; odinstalujmy całkowicie TensorFlow z tego Colab.
pip uninstall tensorflow -y -q
Możemy zainstalować TFP na JAX z najnowszymi nocnymi kompilacjami TFP.
pip install -Uq tfp-nightly[jax] > /dev/null
Zaimportujmy kilka przydatnych bibliotek Pythona.
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn import datasets
sns.set(style='white')
/usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead. import pandas.util.testing as tm
Zaimportujmy również kilka podstawowych funkcji JAX.
import jax.numpy as jnp
from jax import grad
from jax import jit
from jax import random
from jax import value_and_grad
from jax import vmap
Importowanie TFP na JAX
Aby korzystać TFP na JAX, wystarczy zaimportować jax „podłoża” i używać go jak zwykle będzie tfp :
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
tfpk = tfp.math.psd_kernels
Demo: Bayesowska regresja logistyczna
Aby zademonstrować, co możemy zrobić z backendem JAX, zaimplementujemy bayesowską regresję logistyczną stosowaną do klasycznego zestawu danych Iris.
Najpierw zaimportujmy zestaw danych Iris i wyodrębnijmy kilka metadanych.
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
Możemy zdefiniować model używając tfd.JointDistributionCoroutine . Umieścimy standardowe normalne prawdopodobieństwa a priori na obu wag i określenia polaryzacji następnie napisać target_log_prob funkcję szpilki objętych próbą etykiet do danych.
Root = tfd.JointDistributionCoroutine.Root
def model():
w = yield Root(tfd.Sample(tfd.Normal(0., 1.),
sample_shape=(num_features, num_classes)))
b = yield Root(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(num_classes,)))
logits = jnp.dot(features, w) + b
yield tfd.Independent(tfd.Categorical(logits=logits),
reinterpreted_batch_ndims=1)
dist = tfd.JointDistributionCoroutine(model)
def target_log_prob(*params):
return dist.log_prob(params + (labels,))
Mamy próbki z dist do wytworzenia stanu początkowego dla MCMC. Następnie możemy zdefiniować funkcję, która przyjmuje losowy klucz i stan początkowy, i tworzy 500 próbek z próbnika bez zawracania (NUTS). Należy pamiętać, że możemy użyć transformacje JAX jak jit skompilować nasz NUTS próbnika za pomocą XLA.
init_key, sample_key = random.split(random.PRNGKey(0))
init_params = tuple(dist.sample(seed=init_key)[:-1])
@jit
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-3)
return tfp.mcmc.sample_chain(500,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
num_burnin_steps=500,
seed=key)
states, log_probs = run_chain(sample_key, init_params)
plt.figure()
plt.plot(log_probs)
plt.ylabel('Target Log Prob')
plt.xlabel('Iterations of NUTS')
plt.show()
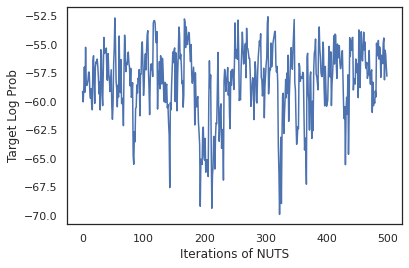
Użyjmy naszych próbek, aby wykonać uśrednianie modelu bayesowskiego (BMA) przez uśrednienie przewidywanych prawdopodobieństw każdego zestawu wag.
Najpierw napiszmy funkcję, która dla danego zestawu parametrów wygeneruje prawdopodobieństwa dla każdej klasy. Możemy użyć dist.sample_distributions do uzyskania ostatecznego rozkładu w modelu.
def classifier_probs(params):
dists, _ = dist.sample_distributions(seed=random.PRNGKey(0),
value=params + (None,))
return dists[-1].distribution.probs_parameter()
Możemy vmap(classifier_probs) na zestaw próbek, aby uzyskać przewidywane prawdopodobieństwo klasy dla każdego z naszych próbek. Następnie obliczamy średnią dokładność w każdej próbce oraz dokładność z uśredniania modelu bayesowskiego.
all_probs = jit(vmap(classifier_probs))(states)
print('Average accuracy:', jnp.mean(all_probs.argmax(axis=-1) == labels))
print('BMA accuracy:', jnp.mean(all_probs.mean(axis=0).argmax(axis=-1) == labels))
Average accuracy: 0.96952 BMA accuracy: 0.97999996
Wygląda na to, że BMA zmniejsza nasz wskaźnik błędów o prawie jedną trzecią!
Podstawy
TFP na JAX ma identyczną API TF gdzie zamiast przyjmowania przedmiotów TF jak tf.Tensor Ś przyjmuje analog JAX. Na przykład, gdziekolwiek tf.Tensor był używany jako wejście API się oczekuje JAX DeviceArray . Zamiast zwracania tf.Tensor metody TFP powróci DeviceArray s. TFP na JAX współpracuje również z zagnieżdżonych struktur obiektów JAX, takich jak listy lub słownika DeviceArray s.
Dystrybucje
Większość dystrybucji TFP jest obsługiwana w JAX z bardzo podobną semantyką do ich odpowiedników TF. Są one również zarejestrowany jako JAX Pytrees , więc mogą być wejścia i wyjścia z JAX-przekształconych funkcji.
Podstawowe dystrybucje
log_prob metoda dystrybucji działa tak samo.
dist = tfd.Normal(0., 1.)
print(dist.log_prob(0.))
-0.9189385
Pobieranie próbek z rozkładu wymaga wyraźnie przechodzącą w PRNGKey (lub listę liczb całkowitych) jako seed argumentu słowa kluczowego. Niepowodzenie jawnego przekazania nasion spowoduje błąd.
tfd.Normal(0., 1.).sample(seed=random.PRNGKey(0))
DeviceArray(-0.20584226, dtype=float32)
Semantyka kształt rozkładów pozostają takie same w JAX, gdzie każdy będzie dystrybucje mieć event_shape i batch_shape i rysowania wielu próbek doda dodatkowe sample_shape wymiary.
Na przykład, tfd.MultivariateNormalDiag parametry wektora będzie mieć kształt zdarzeń wektora i pusty kształt wsadu.
dist = tfd.MultivariateNormalDiag(
loc=jnp.zeros(5),
scale_diag=jnp.ones(5)
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: (5,) Batch shape: ()
Z drugiej strony, tfd.Normal parametryzowane wektorami będą miały kształt skalarne i wektorowe wydarzenie partii kształt.
dist = tfd.Normal(
loc=jnp.ones(5),
scale=jnp.ones(5),
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: () Batch shape: (5,)
Semantyka biorąc log_prob próbek działa tak samo w JAX też.
dist = tfd.Normal(jnp.zeros(5), jnp.ones(5))
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
dist = tfd.Independent(tfd.Normal(jnp.zeros(5), jnp.ones(5)), 1)
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
(10, 2, 5) (10, 2)
Ponieważ JAX DeviceArray s są kompatybilne z bibliotekami jak NumPy i matplotlib, możemy nakarmić próbek bezpośrednio do funkcji kreślenia.
sns.distplot(tfd.Normal(0., 1.).sample(1000, seed=random.PRNGKey(0)))
plt.show()
Distribution metody są zgodne z przekształceń JAX.
sns.distplot(jit(vmap(lambda key: tfd.Normal(0., 1.).sample(seed=key)))(
random.split(random.PRNGKey(0), 2000)))
plt.show()
x = jnp.linspace(-5., 5., 100)
plt.plot(x, jit(vmap(grad(tfd.Normal(0., 1.).prob)))(x))
plt.show()
Ponieważ dystrybucje TFP są zarejestrowane jako JAX węzłów pytree, możemy napisać funkcje z rozkładami jak wejść lub wyjść i przekształcić je za pomocą jit , ale nie są jeszcze obsługiwane jako argumenty vmap funkcje -ed.
@jit
def random_distribution(key):
loc_key, scale_key = random.split(key)
loc, log_scale = random.normal(loc_key), random.normal(scale_key)
return tfd.Normal(loc, jnp.exp(log_scale))
random_dist = random_distribution(random.PRNGKey(0))
print(random_dist.mean(), random_dist.variance())
0.14389051 0.081832744
Przekształcone dystrybucje
Przekształcone dystrybucje tj dystrybucje, których próbki są przepuszczane przez Bijector również pracować z pudełka (bijectors działa też! Patrz poniżej).
dist = tfd.TransformedDistribution(
tfd.Normal(0., 1.),
tfb.Sigmoid()
)
sns.distplot(dist.sample(1000, seed=random.PRNGKey(0)))
plt.show()
Wspólne dystrybucje
TFP oferuje JointDistribution s, aby umożliwić łączenie rozkładu składników w pojedynczym rozkładzie na wielu zmiennych losowych. Obecnie oferuje trzy podstawowe warianty TFP ( JointDistributionSequential , JointDistributionNamed i JointDistributionCoroutine ), z których wszystkie są obsługiwane w JAX. W AutoBatched warianty są również wszystkie obsługiwane.
dist = tfd.JointDistributionSequential([
tfd.Normal(0., 1.),
lambda x: tfd.Normal(x, 1e-1)
])
plt.scatter(*dist.sample(1000, seed=random.PRNGKey(0)), alpha=0.5)
plt.show()
joint = tfd.JointDistributionNamed(dict(
e= tfd.Exponential(rate=1.),
n= tfd.Normal(loc=0., scale=2.),
m=lambda n, e: tfd.Normal(loc=n, scale=e),
x=lambda m: tfd.Sample(tfd.Bernoulli(logits=m), 12),
))
joint.sample(seed=random.PRNGKey(0))
{'e': DeviceArray(3.376818, dtype=float32),
'm': DeviceArray(2.5449684, dtype=float32),
'n': DeviceArray(-0.6027825, dtype=float32),
'x': DeviceArray([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int32)}
Root = tfd.JointDistributionCoroutine.Root
def model():
e = yield Root(tfd.Exponential(rate=1.))
n = yield Root(tfd.Normal(loc=0, scale=2.))
m = yield tfd.Normal(loc=n, scale=e)
x = yield tfd.Sample(tfd.Bernoulli(logits=m), 12)
joint = tfd.JointDistributionCoroutine(model)
joint.sample(seed=random.PRNGKey(0))
StructTuple(var0=DeviceArray(0.17315261, dtype=float32), var1=DeviceArray(-3.290489, dtype=float32), var2=DeviceArray(-3.1949058, dtype=float32), var3=DeviceArray([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], dtype=int32))
Inne dystrybucje
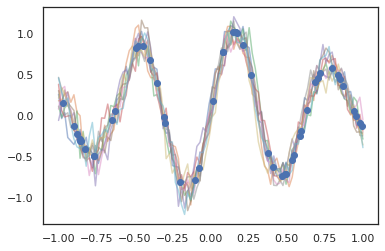
Procesy Gaussa działają również w trybie JAX!
k1, k2, k3 = random.split(random.PRNGKey(0), 3)
observation_noise_variance = 0.01
f = lambda x: jnp.sin(10*x[..., 0]) * jnp.exp(-x[..., 0]**2)
observation_index_points = random.uniform(
k1, [50], minval=-1.,maxval= 1.)[..., jnp.newaxis]
observations = f(observation_index_points) + tfd.Normal(
loc=0., scale=jnp.sqrt(observation_noise_variance)).sample(seed=k2)
index_points = jnp.linspace(-1., 1., 100)[..., jnp.newaxis]
kernel = tfpk.ExponentiatedQuadratic(length_scale=0.1)
gprm = tfd.GaussianProcessRegressionModel(
kernel=kernel,
index_points=index_points,
observation_index_points=observation_index_points,
observations=observations,
observation_noise_variance=observation_noise_variance)
samples = gprm.sample(10, seed=k3)
for i in range(10):
plt.plot(index_points, samples[i], alpha=0.5)
plt.plot(observation_index_points, observations, marker='o', linestyle='')
plt.show()
Obsługiwane są również ukryte modele Markowa.
initial_distribution = tfd.Categorical(probs=[0.8, 0.2])
transition_distribution = tfd.Categorical(probs=[[0.7, 0.3],
[0.2, 0.8]])
observation_distribution = tfd.Normal(loc=[0., 15.], scale=[5., 10.])
model = tfd.HiddenMarkovModel(
initial_distribution=initial_distribution,
transition_distribution=transition_distribution,
observation_distribution=observation_distribution,
num_steps=7)
print(model.mean())
print(model.log_prob(jnp.zeros(7)))
print(model.sample(seed=random.PRNGKey(0)))
[3. 6. 7.5 8.249999 8.625001 8.812501 8.90625 ] /usr/local/lib/python3.6/dist-packages/tensorflow_probability/substrates/jax/distributions/hidden_markov_model.py:483: UserWarning: HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug in which the transition model was applied prior to the initial step. This bug has been fixed. You may observe a slight change in behavior. 'HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug ' -19.855635 [ 1.3641367 0.505798 1.3626463 3.6541772 2.272286 15.10309 22.794212 ]
Kilka dystrybucje takie jak PixelCNN nie są jeszcze obsługiwane z powodu ścisłych zależnościach na TensorFlow lub XLA niezgodności.
Bijektory
Większość bijektorów TFP jest już obsługiwana w JAX!
tfb.Exp().inverse(1.)
DeviceArray(0., dtype=float32)
bij = tfb.Shift(1.)(tfb.Scale(3.))
print(bij.forward(jnp.ones(5)))
print(bij.inverse(jnp.ones(5)))
[4. 4. 4. 4. 4.] [0. 0. 0. 0. 0.]
b = tfb.FillScaleTriL(diag_bijector=tfb.Exp(), diag_shift=None)
print(b.forward(x=[0., 0., 0.]))
print(b.inverse(y=[[1., 0], [.5, 2]]))
[[1. 0.] [0. 1.]] [0.6931472 0.5 0. ]
b = tfb.Chain([tfb.Exp(), tfb.Softplus()])
# or:
# b = tfb.Exp()(tfb.Softplus())
print(b.forward(-jnp.ones(5)))
[1.3678794 1.3678794 1.3678794 1.3678794 1.3678794]
Bijectors są kompatybilne z przekształceń JAX jak jit , grad i vmap .
jit(vmap(tfb.Exp().inverse))(jnp.arange(4.))
DeviceArray([ -inf, 0. , 0.6931472, 1.0986123], dtype=float32)
x = jnp.linspace(0., 1., 100)
plt.plot(x, jit(grad(lambda x: vmap(tfb.Sigmoid().inverse)(x).sum()))(x))
plt.show()
Niektóre bijectors, jak RealNVP i FFJORD nie są jeszcze obsługiwane.
MCMC
Mamy przeniesiony tfp.mcmc Jax, tak więc możemy uruchomić algorytmy jak Hamiltona Monte Carlo (HMC) i No-U-Turn-Sampler (NUTS) w JAX.
target_log_prob = tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)).log_prob
W przeciwieństwie TFP na TF, jesteśmy zobowiązani przekazać PRNGKey do sample_chain pomocą seed argumentu słowa kluczowego.
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-1)
return tfp.mcmc.sample_chain(1000,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
seed=key)
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros(2))
plt.figure()
plt.scatter(*states.T, alpha=0.5)
plt.figure()
plt.plot(log_probs)
plt.show()
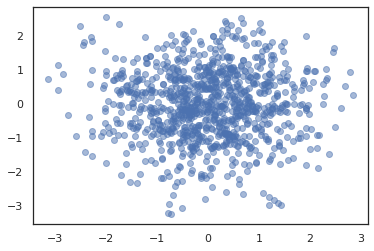
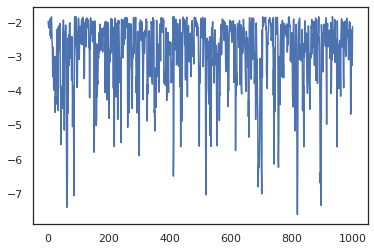
Aby uruchomić wiele łańcuchów, możemy albo przekazać partii państw do sample_chain lub wykorzystanie vmap (choć jeszcze nie zbadane różnice w wynikach pomiędzy dwoma podejściami).
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros([10, 2]))
plt.figure()
for i in range(10):
plt.scatter(*states[:, i].T, alpha=0.5)
plt.figure()
for i in range(10):
plt.plot(log_probs[:, i], alpha=0.5)
plt.show()
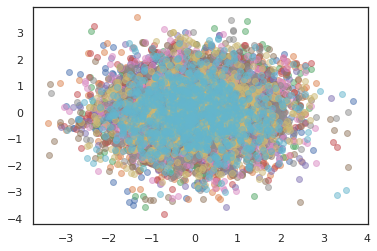
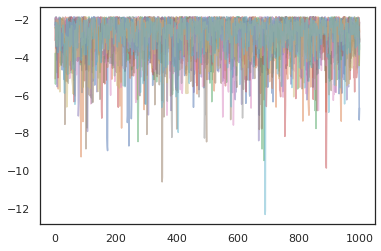
Optymalizatory
TFP w JAX obsługuje kilka ważnych optymalizatorów, takich jak BFGS i L-BFGS. Skonfigurujmy prostą, skalowaną kwadratową funkcję straty.
minimum = jnp.array([1.0, 1.0]) # The center of the quadratic bowl.
scales = jnp.array([2.0, 3.0]) # The scales along the two axes.
# The objective function and the gradient.
def quadratic_loss(x):
return jnp.sum(scales * jnp.square(x - minimum))
start = jnp.array([0.6, 0.8]) # Starting point for the search.
BFGS może znaleźć minimum tej straty.
optim_results = tfp.optimizer.bfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
Tak samo L-BFGS.
optim_results = tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
Aby vmap L-BFGS, Ustawmy funkcji, która optymalizuje stratę jednego punktu początkowego.
def optimize_single(start):
return tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
all_results = jit(vmap(optimize_single))(
random.normal(random.PRNGKey(0), (10, 2)))
assert all(all_results.converged)
for i in range(10):
np.testing.assert_allclose(optim_results.position[i], minimum)
print("Function evaluations: %s" % all_results.num_objective_evaluations)
Function evaluations: [6 6 9 6 6 8 6 8 5 9]
Zastrzeżenia
Istnieją pewne podstawowe różnice między TF i JAX, niektóre zachowania TFP będą się różnić między dwoma podłożami i nie wszystkie funkcje są obsługiwane. Na przykład,
- TFP na JAX nie obsługuje niczego podobnego
tf.Variableponieważ nic tak jak to występuje w JAX. Oznacza to także narzędzia takie jaktfp.util.TransformedVariablenie są obsługiwane albo. -
tfp.layersnie jest obsługiwana w backend jeszcze, ze względu na uzależnienie od Keras itf.Variables. -
tfp.math.minimizenie działa w TFP na JAX powodu jego uzależnienia odtf.Variable. - W TFP na JAX, kształty tensorów są zawsze konkretnymi wartościami całkowitymi i nigdy nie są nieznane/dynamiczne, jak w TFP na TF.
- Pseudolosowość jest inaczej traktowana w TF i JAX (patrz załącznik).
- Biblioteki w
tfp.experimentalnie są gwarantowane istnieć w podłożu JAX. - Zasady promocji Dtype są różne w TF i JAX. TFP na JAX próbuje wewnętrznie respektować semantykę dtype TF, aby zapewnić spójność.
- Bijektory nie zostały jeszcze zarejestrowane jako pytrees JAX.
Aby zobaczyć pełną listę tego, co jest obsługiwana w TFP na JAX, należy zapoznać się z dokumentacją API .
Wniosek
Przenieśliśmy wiele funkcji TFP do JAX i nie możemy się doczekać, co zbudują wszyscy. Niektóre funkcje nie są jeszcze obsługiwane; jeśli straciłeś coś ważnego do ciebie (lub jeśli znajdziesz błąd!), skontaktuj się z nami - można wysłać tfprobability@tensorflow.org lub złożyć sprawę na naszej repo GitHub .
Dodatek: pseudolosowość w JAX
Model Jax generowania liczb pseudolosowych jest (PRNG) jest bezpaństwowcem. W przeciwieństwie do modelu stanowego, nie ma zmiennego stanu globalnego, który ewoluuje po każdym losowym losowaniu. W modelu Jax jest, zaczynamy z kluczem PRNG, który działa jak para 32-bitowych liczb całkowitych. Możemy skonstruować za pomocą tych klawiszy jax.random.PRNGKey .
key = random.PRNGKey(0) # Creates a key with value [0, 0]
print(key)
[0 0]
Losowo wybrane funkcje w JAX spożywać klucza do deterministycznie produkować losową variate, co oznacza, że nie powinny być używane ponownie. Na przykład, możemy użyć key do próbki o rozkładzie normalnym wartość, ale nie powinno się używać key ponownie w innym miejscu. Ponadto, podając tę samą wartość na random.normal spowoduje taką samą wartość.
print(random.normal(key))
-0.20584226
Jak więc pobrać wiele próbek z jednego klucza? Odpowiedź jest kluczem łupania. Podstawowym założeniem jest to, że możemy podzielić PRNGKey na wiele, a każdy z nowych kluczy mogą być traktowane jako niezależne źródło losowości.
key1, key2 = random.split(key, num=2)
print(key1, key2)
[4146024105 967050713] [2718843009 1272950319]
Podział kluczy jest deterministyczny, ale chaotyczny, więc każdy nowy klucz może być teraz używany do losowania odrębnej próby.
print(random.normal(key1), random.normal(key2))
0.14389051 -1.2515389
Więcej informacji na temat modelu deterministycznego łupania klucz Jax, patrz tej instrukcji .
