 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza l'origine su GitHub Visualizza l'origine su GitHub |  Scarica quaderno Scarica quaderno |
Tensorflow Probabilità (TFP) è una libreria per ragionamento probabilistico e l'analisi statistica che ora funziona anche su JAX ! Per chi non lo conoscesse, JAX è una libreria per il calcolo numerico accelerato basata su trasformazioni di funzioni componibili.
TFP su JAX supporta molte delle funzionalità più utili della normale TFP preservando le astrazioni e le API con cui molti utenti di TFP si trovano ora a proprio agio.
Impostare
TFP su JAX non dipende tensorflow; disinstalliamo completamente TensorFlow da questo Colab.
pip uninstall tensorflow -y -q
Possiamo installare TFP su JAX con le ultime build notturne di TFP.
pip install -Uq tfp-nightly[jax] > /dev/null
Importiamo alcune utili librerie Python.
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn import datasets
sns.set(style='white')
/usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead. import pandas.util.testing as tm
Importiamo anche alcune funzionalità JAX di base.
import jax.numpy as jnp
from jax import grad
from jax import jit
from jax import random
from jax import value_and_grad
from jax import vmap
Importare TFP su JAX
Per utilizzare TFP su JAX, è sufficiente importare il jax "substrato" e usarlo come la normale procedura tfp :
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
tfpk = tfp.math.psd_kernels
Demo: regressione logistica bayesiana
Per dimostrare cosa possiamo fare con il backend JAX, implementeremo la regressione logistica bayesiana applicata al classico set di dati Iris.
Per prima cosa, importiamo il set di dati Iris ed estraiamo alcuni metadati.
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
Possiamo definire il modello utilizzando tfd.JointDistributionCoroutine . Metteremo priori normali standard su entrambi i pesi e il termine bias di poi scrivere la target_log_prob funzione che i perni delle etichette campionati ai dati.
Root = tfd.JointDistributionCoroutine.Root
def model():
w = yield Root(tfd.Sample(tfd.Normal(0., 1.),
sample_shape=(num_features, num_classes)))
b = yield Root(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(num_classes,)))
logits = jnp.dot(features, w) + b
yield tfd.Independent(tfd.Categorical(logits=logits),
reinterpreted_batch_ndims=1)
dist = tfd.JointDistributionCoroutine(model)
def target_log_prob(*params):
return dist.log_prob(params + (labels,))
Noi campione dal dist per produrre uno stato iniziale per MCMC. Possiamo quindi definire una funzione che prende in una chiave casuale e uno stato iniziale e produce 500 campioni da un campionatore No-U-Turn (NUTS). Si noti che possiamo usare trasformazioni JAX come jit per compilare il nostro campionatore NUTS utilizzando XLA.
init_key, sample_key = random.split(random.PRNGKey(0))
init_params = tuple(dist.sample(seed=init_key)[:-1])
@jit
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-3)
return tfp.mcmc.sample_chain(500,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
num_burnin_steps=500,
seed=key)
states, log_probs = run_chain(sample_key, init_params)
plt.figure()
plt.plot(log_probs)
plt.ylabel('Target Log Prob')
plt.xlabel('Iterations of NUTS')
plt.show()
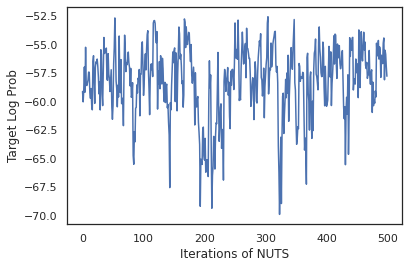
Usiamo i nostri campioni per eseguire la media del modello bayesiano (BMA) calcolando la media delle probabilità previste di ciascun insieme di pesi.
Per prima cosa scriviamo una funzione che per un dato insieme di parametri produrrà le probabilità su ogni classe. Possiamo usare dist.sample_distributions per ottenere la distribuzione finale nel modello.
def classifier_probs(params):
dists, _ = dist.sample_distributions(seed=random.PRNGKey(0),
value=params + (None,))
return dists[-1].distribution.probs_parameter()
Siamo in grado di vmap(classifier_probs) il gruppo di campioni per ottenere le probabilità di classe previsti per ciascuno dei nostri campioni. Quindi calcoliamo l'accuratezza media su ciascun campione e l'accuratezza dalla media del modello bayesiano.
all_probs = jit(vmap(classifier_probs))(states)
print('Average accuracy:', jnp.mean(all_probs.argmax(axis=-1) == labels))
print('BMA accuracy:', jnp.mean(all_probs.mean(axis=0).argmax(axis=-1) == labels))
Average accuracy: 0.96952 BMA accuracy: 0.97999996
Sembra che BMA riduca il nostro tasso di errore di quasi un terzo!
Fondamenti
TFP su JAX ha un'API identica a TF dove invece di accettare oggetti TF come tf.Tensor s accetta l'analogico JAX. Ad esempio, laddove un tf.Tensor stato precedentemente utilizzato come input, l'API ora aspetta un JAX DeviceArray . Invece di restituire un tf.Tensor , metodi TFP torneranno DeviceArray s. TFP su JAX funziona anche con strutture annidate di oggetti JAX, come una lista o un dizionario di DeviceArray s.
distribuzioni
La maggior parte delle distribuzioni di TFP sono supportate in JAX con una semantica molto simile alle loro controparti TF. Essi sono anche registrati come JAX Pytrees , in modo che possano essere ingressi e le uscite delle funzioni JAX-trasformate.
distribuzioni di base
Il log_prob metodo per distribuzioni funziona allo stesso modo.
dist = tfd.Normal(0., 1.)
print(dist.log_prob(0.))
-0.9189385
Campionamento da una distribuzione richiede esplicitamente che passa in un PRNGKey (o un elenco di numeri interi) come il seed argomento parola chiave. Non riuscire a passare esplicitamente un seme genererà un errore.
tfd.Normal(0., 1.).sample(seed=random.PRNGKey(0))
DeviceArray(-0.20584226, dtype=float32)
La semantica forma per distribuzioni rimangono invariati in JAX, dove le distribuzioni hanno ciascuno un event_shape e batch_shape e disegno molti campioni aggiungerà ulteriori sample_shape dimensioni.
Ad esempio, un tfd.MultivariateNormalDiag con parametri vettore avrà una forma evento vettoriale e forma batch vuoto.
dist = tfd.MultivariateNormalDiag(
loc=jnp.zeros(5),
scale_diag=jnp.ones(5)
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: (5,) Batch shape: ()
D'altra parte, un tfd.Normal parametrizzato con vettori avrà una forma forma evento e vettoriale lotto scalare.
dist = tfd.Normal(
loc=jnp.ones(5),
scale=jnp.ones(5),
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: () Batch shape: (5,)
La semantica di prendere log_prob di campioni funziona lo stesso in JAX troppo.
dist = tfd.Normal(jnp.zeros(5), jnp.ones(5))
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
dist = tfd.Independent(tfd.Normal(jnp.zeros(5), jnp.ones(5)), 1)
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
(10, 2, 5) (10, 2)
Perché JAX DeviceArray s sono compatibili con le librerie come NumPy e Matplotlib, siamo in grado di nutrire i campioni direttamente in una funzione di stampa.
sns.distplot(tfd.Normal(0., 1.).sample(1000, seed=random.PRNGKey(0)))
plt.show()
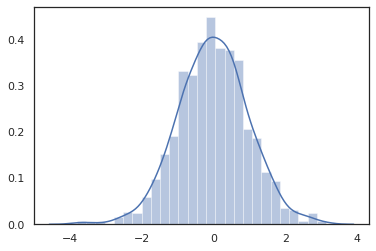
Distribution metodi sono compatibili con le trasformazioni JAX.
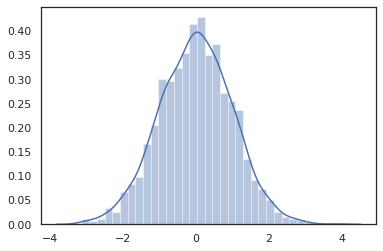
sns.distplot(jit(vmap(lambda key: tfd.Normal(0., 1.).sample(seed=key)))(
random.split(random.PRNGKey(0), 2000)))
plt.show()
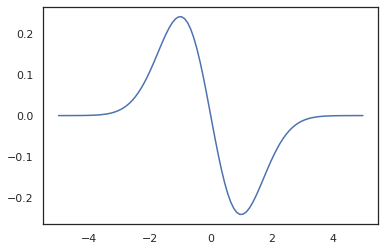
x = jnp.linspace(-5., 5., 100)
plt.plot(x, jit(vmap(grad(tfd.Normal(0., 1.).prob)))(x))
plt.show()
Poiché distribuzioni TFP sono registrati come JAX nodi pytree, possiamo scrivere funzioni con distribuzioni come ingressi o uscite e trasformarli utilizzando jit , ma non sono ancora supportato come argomenti vmap funzioni -ed.
@jit
def random_distribution(key):
loc_key, scale_key = random.split(key)
loc, log_scale = random.normal(loc_key), random.normal(scale_key)
return tfd.Normal(loc, jnp.exp(log_scale))
random_dist = random_distribution(random.PRNGKey(0))
print(random_dist.mean(), random_dist.variance())
0.14389051 0.081832744
Distribuzioni trasformate
Distribuzioni trasformati cioè distribuzioni cui campioni sono passati attraverso un Bijector opera anche fuori dalla scatola (bijectors lavorano troppo! Vedi sotto).
dist = tfd.TransformedDistribution(
tfd.Normal(0., 1.),
tfb.Sigmoid()
)
sns.distplot(dist.sample(1000, seed=random.PRNGKey(0)))
plt.show()
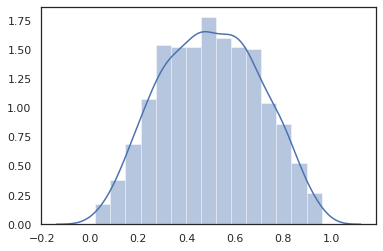
Distribuzioni congiunte
TFP offre JointDistribution s per consentire combinando distribuzioni componenti in un'unica distribuzione su più variabili casuali. Attualmente, TFP offerte tre varianti principali ( JointDistributionSequential , JointDistributionNamed e JointDistributionCoroutine ) i quali sono supportati in JAX. I AutoBatched varianti sono tutti supportati.
dist = tfd.JointDistributionSequential([
tfd.Normal(0., 1.),
lambda x: tfd.Normal(x, 1e-1)
])
plt.scatter(*dist.sample(1000, seed=random.PRNGKey(0)), alpha=0.5)
plt.show()
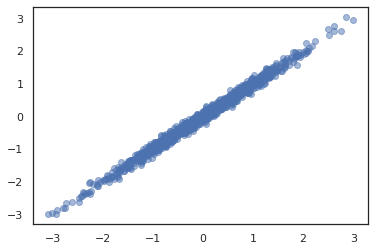
joint = tfd.JointDistributionNamed(dict(
e= tfd.Exponential(rate=1.),
n= tfd.Normal(loc=0., scale=2.),
m=lambda n, e: tfd.Normal(loc=n, scale=e),
x=lambda m: tfd.Sample(tfd.Bernoulli(logits=m), 12),
))
joint.sample(seed=random.PRNGKey(0))
{'e': DeviceArray(3.376818, dtype=float32),
'm': DeviceArray(2.5449684, dtype=float32),
'n': DeviceArray(-0.6027825, dtype=float32),
'x': DeviceArray([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int32)}
Root = tfd.JointDistributionCoroutine.Root
def model():
e = yield Root(tfd.Exponential(rate=1.))
n = yield Root(tfd.Normal(loc=0, scale=2.))
m = yield tfd.Normal(loc=n, scale=e)
x = yield tfd.Sample(tfd.Bernoulli(logits=m), 12)
joint = tfd.JointDistributionCoroutine(model)
joint.sample(seed=random.PRNGKey(0))
StructTuple(var0=DeviceArray(0.17315261, dtype=float32), var1=DeviceArray(-3.290489, dtype=float32), var2=DeviceArray(-3.1949058, dtype=float32), var3=DeviceArray([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], dtype=int32))
Altre distribuzioni
I processi gaussiani funzionano anche in modalità JAX!
k1, k2, k3 = random.split(random.PRNGKey(0), 3)
observation_noise_variance = 0.01
f = lambda x: jnp.sin(10*x[..., 0]) * jnp.exp(-x[..., 0]**2)
observation_index_points = random.uniform(
k1, [50], minval=-1.,maxval= 1.)[..., jnp.newaxis]
observations = f(observation_index_points) + tfd.Normal(
loc=0., scale=jnp.sqrt(observation_noise_variance)).sample(seed=k2)
index_points = jnp.linspace(-1., 1., 100)[..., jnp.newaxis]
kernel = tfpk.ExponentiatedQuadratic(length_scale=0.1)
gprm = tfd.GaussianProcessRegressionModel(
kernel=kernel,
index_points=index_points,
observation_index_points=observation_index_points,
observations=observations,
observation_noise_variance=observation_noise_variance)
samples = gprm.sample(10, seed=k3)
for i in range(10):
plt.plot(index_points, samples[i], alpha=0.5)
plt.plot(observation_index_points, observations, marker='o', linestyle='')
plt.show()
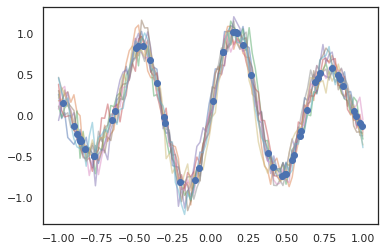
Sono supportati anche i modelli Markov nascosti.
initial_distribution = tfd.Categorical(probs=[0.8, 0.2])
transition_distribution = tfd.Categorical(probs=[[0.7, 0.3],
[0.2, 0.8]])
observation_distribution = tfd.Normal(loc=[0., 15.], scale=[5., 10.])
model = tfd.HiddenMarkovModel(
initial_distribution=initial_distribution,
transition_distribution=transition_distribution,
observation_distribution=observation_distribution,
num_steps=7)
print(model.mean())
print(model.log_prob(jnp.zeros(7)))
print(model.sample(seed=random.PRNGKey(0)))
[3. 6. 7.5 8.249999 8.625001 8.812501 8.90625 ] /usr/local/lib/python3.6/dist-packages/tensorflow_probability/substrates/jax/distributions/hidden_markov_model.py:483: UserWarning: HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug in which the transition model was applied prior to the initial step. This bug has been fixed. You may observe a slight change in behavior. 'HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug ' -19.855635 [ 1.3641367 0.505798 1.3626463 3.6541772 2.272286 15.10309 22.794212 ]
Poche distribuzioni come PixelCNN non sono ancora supportati a causa di severe dipendenze tensorflow o XLA incompatibilità.
Biiettori
La maggior parte dei biiettori di TFP sono supportati in JAX oggi!
tfb.Exp().inverse(1.)
DeviceArray(0., dtype=float32)
bij = tfb.Shift(1.)(tfb.Scale(3.))
print(bij.forward(jnp.ones(5)))
print(bij.inverse(jnp.ones(5)))
[4. 4. 4. 4. 4.] [0. 0. 0. 0. 0.]
b = tfb.FillScaleTriL(diag_bijector=tfb.Exp(), diag_shift=None)
print(b.forward(x=[0., 0., 0.]))
print(b.inverse(y=[[1., 0], [.5, 2]]))
[[1. 0.] [0. 1.]] [0.6931472 0.5 0. ]
b = tfb.Chain([tfb.Exp(), tfb.Softplus()])
# or:
# b = tfb.Exp()(tfb.Softplus())
print(b.forward(-jnp.ones(5)))
[1.3678794 1.3678794 1.3678794 1.3678794 1.3678794]
Bijectors sono compatibili con le trasformazioni JAX come jit , grad e vmap .
jit(vmap(tfb.Exp().inverse))(jnp.arange(4.))
DeviceArray([ -inf, 0. , 0.6931472, 1.0986123], dtype=float32)
x = jnp.linspace(0., 1., 100)
plt.plot(x, jit(grad(lambda x: vmap(tfb.Sigmoid().inverse)(x).sum()))(x))
plt.show()
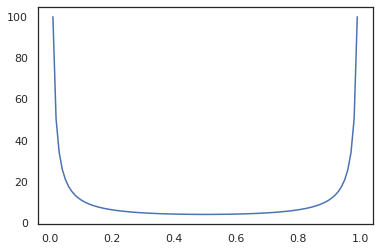
Alcuni bijectors, come RealNVP e FFJORD non sono ancora supportati.
MCMC
Abbiamo porting tfp.mcmc a JAX pure, in modo da poter eseguire algoritmi come Hamiltoniana Monte Carlo (HMC) e il No-U-Turn-Sampler (NUTS) in JAX.
target_log_prob = tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)).log_prob
A differenza di TFP il TF, ci viene richiesto di passare un PRNGKey in sample_chain utilizzando il seed argomento chiave.
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-1)
return tfp.mcmc.sample_chain(1000,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
seed=key)
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros(2))
plt.figure()
plt.scatter(*states.T, alpha=0.5)
plt.figure()
plt.plot(log_probs)
plt.show()
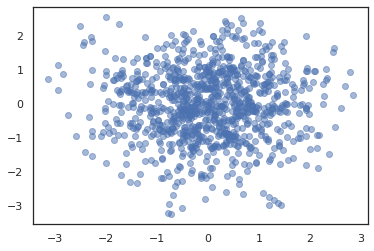
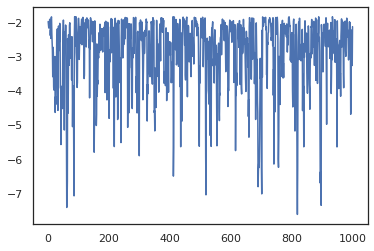
Per eseguire più catene, possiamo sia passare una serie di Stati in sample_chain o l'uso vmap (anche se non abbiamo ancora esplorato differenze di prestazioni tra i due approcci).
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros([10, 2]))
plt.figure()
for i in range(10):
plt.scatter(*states[:, i].T, alpha=0.5)
plt.figure()
for i in range(10):
plt.plot(log_probs[:, i], alpha=0.5)
plt.show()
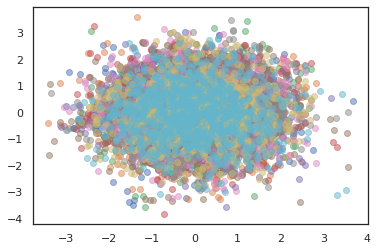
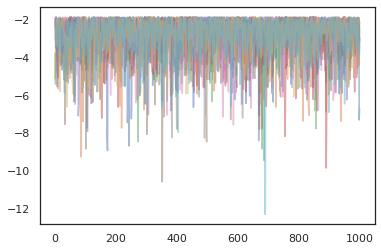
ottimizzatori
TFP su JAX supporta alcuni importanti ottimizzatori come BFGS e L-BFGS. Impostiamo una semplice funzione di perdita quadratica in scala.
minimum = jnp.array([1.0, 1.0]) # The center of the quadratic bowl.
scales = jnp.array([2.0, 3.0]) # The scales along the two axes.
# The objective function and the gradient.
def quadratic_loss(x):
return jnp.sum(scales * jnp.square(x - minimum))
start = jnp.array([0.6, 0.8]) # Starting point for the search.
BFGS può trovare il minimo di questa perdita.
optim_results = tfp.optimizer.bfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
Così può L-BFGS.
optim_results = tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
Per vmap L-BFGS, facciamo impostare una funzione che ottimizza la perdita di un singolo punto di partenza.
def optimize_single(start):
return tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
all_results = jit(vmap(optimize_single))(
random.normal(random.PRNGKey(0), (10, 2)))
assert all(all_results.converged)
for i in range(10):
np.testing.assert_allclose(optim_results.position[i], minimum)
print("Function evaluations: %s" % all_results.num_objective_evaluations)
Function evaluations: [6 6 9 6 6 8 6 8 5 9]
Avvertenze
Esistono alcune differenze fondamentali tra TF e JAX, alcuni comportamenti TFP saranno diversi tra i due substrati e non tutte le funzionalità sono supportate. Per esempio,
- TFP su JAX non supporta nulla di simile
tf.Variablepoiché nulla di simile esiste in JAX. Questo significa anche utilità cometfp.util.TransformedVariablenon sono supportati neanche. -
tfp.layersnon è ancora supportato nel backend, a causa della sua dipendenza Keras etf.Variables. -
tfp.math.minimizenon funziona in TFP su JAX a causa della sua dipendenza datf.Variable. - Con TFP su JAX, le forme tensoriali sono sempre valori interi concreti e non sono mai sconosciute/dinamiche come in TFP su TF.
- La pseudocasualità è gestita in modo diverso in TF e JAX (vedi appendice).
- Biblioteche in
tfp.experimentalnon sono garantiti esistere nel substrato JAX. - Le regole di promozione Dtype sono diverse tra TF e JAX. TFP su JAX cerca di rispettare la semantica dtype di TF internamente, per coerenza.
- I biiettori non sono ancora stati registrati come pytree JAX.
Per visualizzare l'elenco completo di ciò che è supportato in TFP su JAX, si prega di fare riferimento alla documentazione API .
Conclusione
Abbiamo portato molte delle funzionalità di TFP su JAX e non vediamo l'ora di vedere cosa costruiranno tutti. Alcune funzionalità non sono ancora supportate; se abbiamo perso qualcosa di importante per voi (o se si trova un bug!) rivolgiti a noi - si può e-mail tfprobability@tensorflow.org o file un problema sulla nostra repo Github .
Appendice: pseudocasualità in JAX
Il modello di JAX generazione di numeri pseudo (PRNG) è senza stato. A differenza di un modello stateful, non esiste uno stato globale mutevole che si evolve dopo ogni estrazione casuale. Nel modello di JAX, iniziamo con una chiave PRNG, che agisce come un paio di interi a 32 bit. Siamo in grado di costruire questi chiavi utilizzando jax.random.PRNGKey .
key = random.PRNGKey(0) # Creates a key with value [0, 0]
print(key)
[0 0]
Funzioni casuali in JAX consumano una chiave per deterministicamente produrre una variata a caso, nel senso che non devono essere utilizzati di nuovo. Per esempio, possiamo usare key per campionare un valore distribuito normalmente, ma non dobbiamo usare key di nuovo altrove. Inoltre, superato lo stesso valore in random.normal produrrà lo stesso valore.
print(random.normal(key))
-0.20584226
Quindi, come possiamo disegnare più campioni da una singola chiave? La risposta è la divisione chiave. L'idea di base è che possiamo dividere un PRNGKey in multiplo, e ciascuna delle nuove chiavi può essere trattata come fonte indipendente di casualità.
key1, key2 = random.split(key, num=2)
print(key1, key2)
[4146024105 967050713] [2718843009 1272950319]
La suddivisione delle chiavi è deterministica ma caotica, quindi ogni nuova chiave può ora essere utilizzata per disegnare un campione casuale distinto.
print(random.normal(key1), random.normal(key2))
0.14389051 -1.2515389
Per maggiori dettagli su deterministica del modello chiave di scissione di JAX, consultare questa guida .
