 Lihat di TensorFlow.org Lihat di TensorFlow.org |  Jalankan di Google Colab Jalankan di Google Colab |  Lihat sumber di GitHub Lihat sumber di GitHub |  Unduh buku catatan Unduh buku catatan |
TensorFlow Probabilitas (TFP) adalah library untuk penalaran probabilistik dan analisis statistik yang kini juga bekerja pada JAX ! Bagi mereka yang tidak terbiasa, JAX adalah perpustakaan untuk komputasi numerik yang dipercepat berdasarkan transformasi fungsi yang dapat dikomposisi.
TFP di JAX mendukung banyak fungsi yang paling berguna dari TFP biasa sambil mempertahankan abstraksi dan API yang sekarang nyaman digunakan oleh banyak pengguna TFP.
Mempersiapkan
TFP pada JAX tidak tergantung pada TensorFlow; mari hapus instalan TensorFlow dari Colab ini sepenuhnya.
pip uninstall tensorflow -y -q
Kami dapat menginstal TFP di JAX dengan build TFP malam terbaru.
pip install -Uq tfp-nightly[jax] > /dev/null
Mari impor beberapa pustaka Python yang berguna.
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn import datasets
sns.set(style='white')
/usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead. import pandas.util.testing as tm
Mari juga mengimpor beberapa fungsi dasar JAX.
import jax.numpy as jnp
from jax import grad
from jax import jit
from jax import random
from jax import value_and_grad
from jax import vmap
Mengimpor TFP di JAX
Untuk menggunakan TFP pada JAX, hanya mengimpor jax "substrat" dan menggunakannya sebagai Anda biasanya akan tfp :
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
tfpk = tfp.math.psd_kernels
Demo: Regresi logistik Bayesian
Untuk mendemonstrasikan apa yang dapat kami lakukan dengan backend JAX, kami akan menerapkan regresi logistik Bayesian yang diterapkan pada set data Iris klasik.
Pertama, mari impor dataset Iris dan ekstrak beberapa metadata.
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
Kita bisa menentukan model menggunakan tfd.JointDistributionCoroutine . Kami akan menempatkan prior standar normal pada kedua bobot dan jangka bias yang kemudian menulis target_log_prob fungsi yang pin label sampel untuk data.
Root = tfd.JointDistributionCoroutine.Root
def model():
w = yield Root(tfd.Sample(tfd.Normal(0., 1.),
sample_shape=(num_features, num_classes)))
b = yield Root(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(num_classes,)))
logits = jnp.dot(features, w) + b
yield tfd.Independent(tfd.Categorical(logits=logits),
reinterpreted_batch_ndims=1)
dist = tfd.JointDistributionCoroutine(model)
def target_log_prob(*params):
return dist.log_prob(params + (labels,))
Kami sampel dari dist untuk menghasilkan keadaan awal untuk MCMC. Kami kemudian dapat mendefinisikan fungsi yang mengambil kunci acak dan keadaan awal, dan menghasilkan 500 sampel dari No-U-Turn-Sampler (NUTS). Perhatikan bahwa kita dapat menggunakan JAX transformasi seperti jit untuk mengkompilasi sampler KACANG kami menggunakan XLA.
init_key, sample_key = random.split(random.PRNGKey(0))
init_params = tuple(dist.sample(seed=init_key)[:-1])
@jit
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-3)
return tfp.mcmc.sample_chain(500,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
num_burnin_steps=500,
seed=key)
states, log_probs = run_chain(sample_key, init_params)
plt.figure()
plt.plot(log_probs)
plt.ylabel('Target Log Prob')
plt.xlabel('Iterations of NUTS')
plt.show()
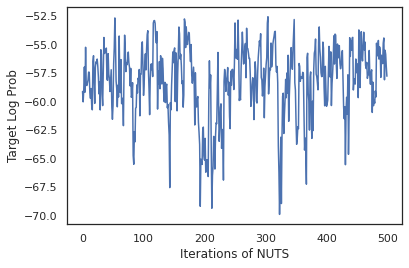
Mari kita gunakan sampel kita untuk melakukan Bayesian model averaging (BMA) dengan merata-ratakan probabilitas yang diprediksi dari setiap rangkaian bobot.
Pertama mari kita tulis sebuah fungsi yang untuk sekumpulan parameter tertentu akan menghasilkan probabilitas untuk setiap kelas. Kita dapat menggunakan dist.sample_distributions untuk mendapatkan distribusi akhir dalam model.
def classifier_probs(params):
dists, _ = dist.sample_distributions(seed=random.PRNGKey(0),
value=params + (None,))
return dists[-1].distribution.probs_parameter()
Kita bisa vmap(classifier_probs) atas set sampel untuk mendapatkan probabilitas kelas diprediksi untuk masing-masing sampel kami. Kami kemudian menghitung akurasi rata-rata di setiap sampel, dan akurasi dari rata-rata model Bayesian.
all_probs = jit(vmap(classifier_probs))(states)
print('Average accuracy:', jnp.mean(all_probs.argmax(axis=-1) == labels))
print('BMA accuracy:', jnp.mean(all_probs.mean(axis=0).argmax(axis=-1) == labels))
Average accuracy: 0.96952 BMA accuracy: 0.97999996
Sepertinya BMA mengurangi tingkat kesalahan kami hampir sepertiga!
Dasar-dasar
TFP pada JAX memiliki API identik dengan TF mana bukannya menerima benda TF seperti tf.Tensor s itu menerima analog JAX. Sebagai contoh, di mana pun tf.Tensor sebelumnya digunakan sebagai masukan, API sekarang mengharapkan JAX DeviceArray . Alih-alih mengembalikan tf.Tensor , metode TFP akan kembali DeviceArray s. TFP pada JAX juga bekerja dengan struktur bersarang benda JAX, seperti daftar atau kamus DeviceArray s.
Distribusi
Sebagian besar distribusi TFP didukung di JAX dengan semantik yang sangat mirip dengan rekanan TF mereka. Mereka juga terdaftar sebagai JAX Pytrees , sehingga mereka dapat menjadi input dan output dari fungsi JAX-berubah.
Distribusi dasar
The log_prob metode untuk distribusi bekerja sama.
dist = tfd.Normal(0., 1.)
print(dist.log_prob(0.))
-0.9189385
Sampling dari distribusi membutuhkan eksplisit lewat di PRNGKey (atau daftar bilangan bulat) sebagai seed argumen kata kunci. Gagal mengirimkan benih secara eksplisit akan menimbulkan kesalahan.
tfd.Normal(0., 1.).sample(seed=random.PRNGKey(0))
DeviceArray(-0.20584226, dtype=float32)
Semantik bentuk untuk distribusi tetap sama di JAX, di mana distribusi masing-masing akan memiliki event_shape dan batch_shape dan menggambar banyak sampel akan menambah tambahan sample_shape dimensi.
Misalnya, tfd.MultivariateNormalDiag dengan parameter vektor akan memiliki bentuk acara vektor dan bentuk batch yang kosong.
dist = tfd.MultivariateNormalDiag(
loc=jnp.zeros(5),
scale_diag=jnp.ones(5)
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: (5,) Batch shape: ()
Di sisi lain, tfd.Normal diparameterisasi dengan vektor akan memiliki skalar acara bentuk dan vektor bets bentuk.
dist = tfd.Normal(
loc=jnp.ones(5),
scale=jnp.ones(5),
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: () Batch shape: (5,)
Semantik mengambil log_prob sampel bekerja sama dalam JAX juga.
dist = tfd.Normal(jnp.zeros(5), jnp.ones(5))
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
dist = tfd.Independent(tfd.Normal(jnp.zeros(5), jnp.ones(5)), 1)
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
(10, 2, 5) (10, 2)
Karena JAX DeviceArray s yang kompatibel dengan perpustakaan seperti NumPy dan Matplotlib, kita bisa memberi makan sampel langsung ke fungsi merencanakan.
sns.distplot(tfd.Normal(0., 1.).sample(1000, seed=random.PRNGKey(0)))
plt.show()
Distribution metode yang kompatibel dengan transformasi JAX.
sns.distplot(jit(vmap(lambda key: tfd.Normal(0., 1.).sample(seed=key)))(
random.split(random.PRNGKey(0), 2000)))
plt.show()
x = jnp.linspace(-5., 5., 100)
plt.plot(x, jit(vmap(grad(tfd.Normal(0., 1.).prob)))(x))
plt.show()
Karena distribusi TFP terdaftar sebagai JAX node pytree, kita bisa menulis fungsi dengan distribusi sebagai input atau output dan mengubah mereka menggunakan jit , tetapi mereka belum didukung sebagai argumen untuk vmap fungsi -ed.
@jit
def random_distribution(key):
loc_key, scale_key = random.split(key)
loc, log_scale = random.normal(loc_key), random.normal(scale_key)
return tfd.Normal(loc, jnp.exp(log_scale))
random_dist = random_distribution(random.PRNGKey(0))
print(random_dist.mean(), random_dist.variance())
0.14389051 0.081832744
Distribusi yang diubah
Distribusi berubah yaitu distribusi yang sampel dilewatkan melalui Bijector juga bekerja di luar kotak (bijectors bekerja terlalu! Lihat di bawah).
dist = tfd.TransformedDistribution(
tfd.Normal(0., 1.),
tfb.Sigmoid()
)
sns.distplot(dist.sample(1000, seed=random.PRNGKey(0)))
plt.show()
Distribusi bersama
TFP menawarkan JointDistribution s untuk memungkinkan menggabungkan distribusi komponen ke dalam distribusi tunggal atas beberapa variabel acak. Saat ini, TFP penawaran tiga varian inti ( JointDistributionSequential , JointDistributionNamed , dan JointDistributionCoroutine ) yang semuanya didukung dalam JAX. The AutoBatched varian juga semua didukung.
dist = tfd.JointDistributionSequential([
tfd.Normal(0., 1.),
lambda x: tfd.Normal(x, 1e-1)
])
plt.scatter(*dist.sample(1000, seed=random.PRNGKey(0)), alpha=0.5)
plt.show()
joint = tfd.JointDistributionNamed(dict(
e= tfd.Exponential(rate=1.),
n= tfd.Normal(loc=0., scale=2.),
m=lambda n, e: tfd.Normal(loc=n, scale=e),
x=lambda m: tfd.Sample(tfd.Bernoulli(logits=m), 12),
))
joint.sample(seed=random.PRNGKey(0))
{'e': DeviceArray(3.376818, dtype=float32),
'm': DeviceArray(2.5449684, dtype=float32),
'n': DeviceArray(-0.6027825, dtype=float32),
'x': DeviceArray([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int32)}
Root = tfd.JointDistributionCoroutine.Root
def model():
e = yield Root(tfd.Exponential(rate=1.))
n = yield Root(tfd.Normal(loc=0, scale=2.))
m = yield tfd.Normal(loc=n, scale=e)
x = yield tfd.Sample(tfd.Bernoulli(logits=m), 12)
joint = tfd.JointDistributionCoroutine(model)
joint.sample(seed=random.PRNGKey(0))
StructTuple(var0=DeviceArray(0.17315261, dtype=float32), var1=DeviceArray(-3.290489, dtype=float32), var2=DeviceArray(-3.1949058, dtype=float32), var3=DeviceArray([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], dtype=int32))
distribusi lainnya
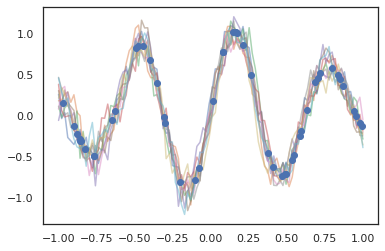
Proses Gaussian juga bekerja dalam mode JAX!
k1, k2, k3 = random.split(random.PRNGKey(0), 3)
observation_noise_variance = 0.01
f = lambda x: jnp.sin(10*x[..., 0]) * jnp.exp(-x[..., 0]**2)
observation_index_points = random.uniform(
k1, [50], minval=-1.,maxval= 1.)[..., jnp.newaxis]
observations = f(observation_index_points) + tfd.Normal(
loc=0., scale=jnp.sqrt(observation_noise_variance)).sample(seed=k2)
index_points = jnp.linspace(-1., 1., 100)[..., jnp.newaxis]
kernel = tfpk.ExponentiatedQuadratic(length_scale=0.1)
gprm = tfd.GaussianProcessRegressionModel(
kernel=kernel,
index_points=index_points,
observation_index_points=observation_index_points,
observations=observations,
observation_noise_variance=observation_noise_variance)
samples = gprm.sample(10, seed=k3)
for i in range(10):
plt.plot(index_points, samples[i], alpha=0.5)
plt.plot(observation_index_points, observations, marker='o', linestyle='')
plt.show()
Model Markov Tersembunyi juga didukung.
initial_distribution = tfd.Categorical(probs=[0.8, 0.2])
transition_distribution = tfd.Categorical(probs=[[0.7, 0.3],
[0.2, 0.8]])
observation_distribution = tfd.Normal(loc=[0., 15.], scale=[5., 10.])
model = tfd.HiddenMarkovModel(
initial_distribution=initial_distribution,
transition_distribution=transition_distribution,
observation_distribution=observation_distribution,
num_steps=7)
print(model.mean())
print(model.log_prob(jnp.zeros(7)))
print(model.sample(seed=random.PRNGKey(0)))
[3. 6. 7.5 8.249999 8.625001 8.812501 8.90625 ] /usr/local/lib/python3.6/dist-packages/tensorflow_probability/substrates/jax/distributions/hidden_markov_model.py:483: UserWarning: HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug in which the transition model was applied prior to the initial step. This bug has been fixed. You may observe a slight change in behavior. 'HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug ' -19.855635 [ 1.3641367 0.505798 1.3626463 3.6541772 2.272286 15.10309 22.794212 ]
Beberapa distribusi seperti PixelCNN tidak didukung belum karena ketergantungan yang ketat pada TensorFlow atau XLA tidak kompatibel.
Bijektor
Sebagian besar bijector TFP didukung di JAX hari ini!
tfb.Exp().inverse(1.)
DeviceArray(0., dtype=float32)
bij = tfb.Shift(1.)(tfb.Scale(3.))
print(bij.forward(jnp.ones(5)))
print(bij.inverse(jnp.ones(5)))
[4. 4. 4. 4. 4.] [0. 0. 0. 0. 0.]
b = tfb.FillScaleTriL(diag_bijector=tfb.Exp(), diag_shift=None)
print(b.forward(x=[0., 0., 0.]))
print(b.inverse(y=[[1., 0], [.5, 2]]))
[[1. 0.] [0. 1.]] [0.6931472 0.5 0. ]
b = tfb.Chain([tfb.Exp(), tfb.Softplus()])
# or:
# b = tfb.Exp()(tfb.Softplus())
print(b.forward(-jnp.ones(5)))
[1.3678794 1.3678794 1.3678794 1.3678794 1.3678794]
Bijectors yang kompatibel dengan transformasi JAX seperti jit , grad dan vmap .
jit(vmap(tfb.Exp().inverse))(jnp.arange(4.))
DeviceArray([ -inf, 0. , 0.6931472, 1.0986123], dtype=float32)
x = jnp.linspace(0., 1., 100)
plt.plot(x, jit(grad(lambda x: vmap(tfb.Sigmoid().inverse)(x).sum()))(x))
plt.show()
Beberapa bijectors, seperti RealNVP dan FFJORD belum didukung.
MCMC
Kami telah porting tfp.mcmc ke JAX juga, sehingga kami dapat menjalankan algoritma seperti Hamiltonian Monte Carlo (HMC) dan No-U-Turn-Sampler (KACANG) di JAX.
target_log_prob = tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)).log_prob
Tidak seperti TFP pada TF, kita dituntut untuk lulus PRNGKey ke sample_chain menggunakan seed argumen kata kunci.
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-1)
return tfp.mcmc.sample_chain(1000,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
seed=key)
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros(2))
plt.figure()
plt.scatter(*states.T, alpha=0.5)
plt.figure()
plt.plot(log_probs)
plt.show()
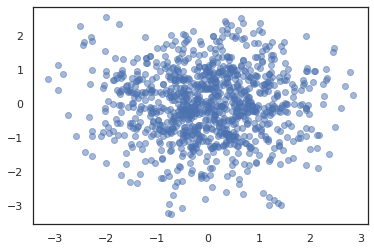
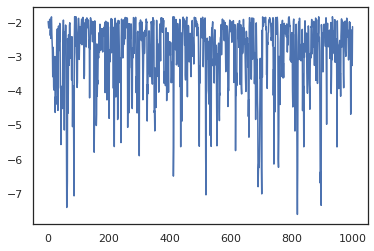
Untuk menjalankan beberapa rantai, kita baik dapat melewati batch negara ke sample_chain atau penggunaan vmap (meskipun kita belum dieksplorasi perbedaan kinerja antara dua pendekatan).
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros([10, 2]))
plt.figure()
for i in range(10):
plt.scatter(*states[:, i].T, alpha=0.5)
plt.figure()
for i in range(10):
plt.plot(log_probs[:, i], alpha=0.5)
plt.show()
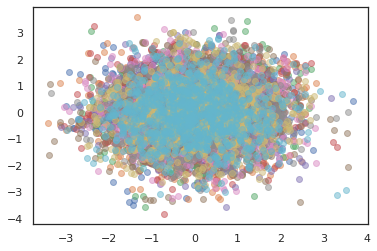
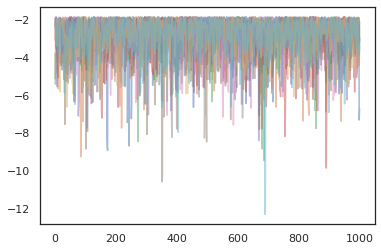
Pengoptimal
TFP di JAX mendukung beberapa pengoptimal penting seperti BFGS dan L-BFGS. Mari kita siapkan fungsi kerugian kuadratik berskala sederhana.
minimum = jnp.array([1.0, 1.0]) # The center of the quadratic bowl.
scales = jnp.array([2.0, 3.0]) # The scales along the two axes.
# The objective function and the gradient.
def quadratic_loss(x):
return jnp.sum(scales * jnp.square(x - minimum))
start = jnp.array([0.6, 0.8]) # Starting point for the search.
BFGS dapat menemukan kerugian minimum ini.
optim_results = tfp.optimizer.bfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
Begitu juga dengan L-BFGS.
optim_results = tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
Untuk vmap L-BFGS, mari kita set terserah fungsi yang mengoptimalkan kerugian bagi titik awal tunggal.
def optimize_single(start):
return tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
all_results = jit(vmap(optimize_single))(
random.normal(random.PRNGKey(0), (10, 2)))
assert all(all_results.converged)
for i in range(10):
np.testing.assert_allclose(optim_results.position[i], minimum)
print("Function evaluations: %s" % all_results.num_objective_evaluations)
Function evaluations: [6 6 9 6 6 8 6 8 5 9]
Peringatan
Ada beberapa perbedaan mendasar antara TF dan JAX, beberapa perilaku TFP akan berbeda antara kedua media dan tidak semua fungsi didukung. Sebagai contoh,
- TFP pada JAX tidak mendukung hal seperti
tf.Variablekarena tidak ada seperti itu ada di JAX. Ini juga berarti utilitas sepertitfp.util.TransformedVariabletidak didukung baik. -
tfp.layerstidak didukung di backend belum, karena ketergantungannya pada Keras dantf.Variables. -
tfp.math.minimizetidak bekerja di TFP pada JAX karena ketergantungannya padatf.Variable. - Dengan TFP di JAX, bentuk tensor selalu merupakan nilai integer konkret dan tidak pernah diketahui/dinamis seperti pada TFP di TF.
- Pseudorandomness ditangani secara berbeda di TF dan JAX (lihat lampiran).
- Perpustakaan di
tfp.experimentaltidak dijamin ada di substrat JAX. - Aturan promosi Dtype berbeda antara TF dan JAX. TFP di JAX mencoba untuk menghormati semantik dtype TF secara internal, untuk konsistensi.
- Bijector belum terdaftar sebagai pytrees JAX.
Untuk melihat daftar lengkap dari apa yang didukung dalam TFP pada JAX, silakan lihat dokumentasi API .
Kesimpulan
Kami telah mem-porting banyak fitur TFP ke JAX dan sangat antusias untuk melihat apa yang akan dibuat semua orang. Beberapa fungsi belum didukung; jika kita telah melewatkan sesuatu yang penting untuk Anda (atau jika Anda menemukan bug!) silakan hubungi kami - Anda dapat mengirim email tfprobability@tensorflow.org atau mengajukan masalah pada repo Github kami .
Lampiran: pseudorandomness di JAX
Jumlah pseudorandom generasi (PRNG) Model JAX adalah stateless. Tidak seperti model stateful, tidak ada state global yang dapat berubah yang berevolusi setelah setiap undian acak. Dalam model JAX, kita mulai dengan kunci PRNG, yang bertindak seperti sepasang 32-bit bilangan bulat. Kita dapat membuat tombol-tombol ini dengan menggunakan jax.random.PRNGKey .
key = random.PRNGKey(0) # Creates a key with value [0, 0]
print(key)
[0 0]
Fungsi acak dalam JAX mengkonsumsi kunci untuk deterministik menghasilkan variate acak, yang berarti mereka tidak boleh digunakan lagi. Sebagai contoh, kita dapat menggunakan key untuk sampel nilai terdistribusi normal, tapi kita tidak harus menggunakan key lagi di tempat lain. Selanjutnya, melewati nilai yang sama dalam random.normal akan menghasilkan nilai yang sama.
print(random.normal(key))
-0.20584226
Jadi bagaimana kita bisa menggambar banyak sampel dari satu kunci? Jawabannya adalah membelah kunci. Ide dasarnya adalah bahwa kita dapat membagi PRNGKey menjadi beberapa, dan masing-masing tombol baru dapat diperlakukan sebagai sumber independen keacakan.
key1, key2 = random.split(key, num=2)
print(key1, key2)
[4146024105 967050713] [2718843009 1272950319]
Pemisahan kunci bersifat deterministik tetapi kacau, sehingga setiap kunci baru sekarang dapat digunakan untuk menggambar sampel acak yang berbeda.
print(random.normal(key1), random.normal(key2))
0.14389051 -1.2515389
Untuk rincian lebih lanjut tentang model kunci membelah deterministik JAX, lihat panduan ini .
