TensorFlow הסתברות ב- JAX

הצג באתר TensorFlow.org

הפעל בגוגל קולאב

צפה במקור ב-GitHub

הורד מחברת

TensorFlow הסתברות (הפריון הכולל) היא ספריה חשיבה הסתברותית וניתוח סטטיסטי עכשיו גם עובד על JAX ! למי שלא מכיר, JAX היא ספרייה למחשוב מספרי מואץ המבוסס על טרנספורמציות של פונקציות הניתנות לחיבור.

TFP ב-JAX תומך בהרבה מהפונקציונליות השימושית ביותר של TFP רגיל תוך שמירה על ההפשטות וממשקי ה-API שמשתמשי TFP רבים חשים איתם כעת.

להכין

הפריון הכולל על JAX אינו תלוי TensorFlow; בואו נסיר לחלוטין את TensorFlow מה-Colab הזה.

pip uninstall tensorflow -y -q

אנחנו יכולים להתקין TFP ב-JAX עם הבנייה הלילית העדכנית ביותר של TFP.

pip install -Uq tfp-nightly[jax] > /dev/null

בואו לייבא כמה ספריות שימושיות של Python.

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn import datasets
sns.set(style='white')

/usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead.
  import pandas.util.testing as tm

בואו לייבא גם כמה פונקציונליות בסיסית של JAX.

import jax.numpy as jnp
from jax import grad
from jax import jit
from jax import random
from jax import value_and_grad
from jax import vmap

ייבוא ​​TFP ב-JAX

כדי להשתמש הפריון הכולל על JAX, פשוט לייבא את jax "המצע" ולהשתמש בו כפי שאתה נוהג להיכנס tfp :

from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
tfpk = tfp.math.psd_kernels

הדגמה: רגרסיה לוגיסטית בייסיאנית

כדי להדגים מה אנחנו יכולים לעשות עם ה-JAX backend, ניישם רגרסיה לוגיסטית בייסיאנית המיושמת על מערך הנתונים הקלאסי של Iris.

ראשית, בואו נייבא את מערך הנתונים של Iris ונחלץ כמה מטא נתונים.

iris = datasets.load_iris()
features, labels = iris['data'], iris['target']

num_features = features.shape[-1]
num_classes = len(iris.target_names)

אנו יכולים להגדיר את המודל באמצעות tfd.JointDistributionCoroutine . נצטרך לשים הרשעות קודמות סטנדרטיות נורמלי הוא המשקולות בטווח ההטיה ואז לכתוב target_log_prob פונקצית סיכות התוויות שנדגמו לנתונים.

Root = tfd.JointDistributionCoroutine.Root
def model():
  w = yield Root(tfd.Sample(tfd.Normal(0., 1.),
                            sample_shape=(num_features, num_classes)))
  b = yield Root(
      tfd.Sample(tfd.Normal(0., 1.), sample_shape=(num_classes,)))
  logits = jnp.dot(features, w) + b
  yield tfd.Independent(tfd.Categorical(logits=logits),
                        reinterpreted_batch_ndims=1)


dist = tfd.JointDistributionCoroutine(model)
def target_log_prob(*params):
  return dist.log_prob(params + (labels,))

אנחנו לטעום מן dist לייצר מצב ראשוני MCMC. לאחר מכן נוכל להגדיר פונקציה שמקבלת מפתח אקראי ומצב התחלתי, ומייצרת 500 דגימות מ-No-Turn-Sampler (NUTS). שים לב כי אנו יכולים להשתמש טרנספורמציות JAX כמו jit כדי לקמפל סמפלר NUTS שלנו באמצעות XLA.

init_key, sample_key = random.split(random.PRNGKey(0))
init_params = tuple(dist.sample(seed=init_key)[:-1])

@jit
def run_chain(key, state):
  kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-3)
  return tfp.mcmc.sample_chain(500,
      current_state=state,
      kernel=kernel,
      trace_fn=lambda _, results: results.target_log_prob,
      num_burnin_steps=500,
      seed=key)

states, log_probs = run_chain(sample_key, init_params)
plt.figure()
plt.plot(log_probs)
plt.ylabel('Target Log Prob')
plt.xlabel('Iterations of NUTS')
plt.show()

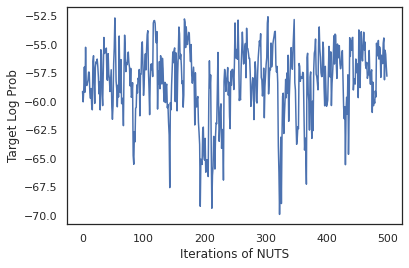
בואו נשתמש בדגימות שלנו כדי לבצע ממוצע מודל בייסיאני (BMA) על ידי ממוצע ההסתברויות החזויות של כל קבוצת משקלים.

ראשית בוא נכתוב פונקציה שעבור קבוצה נתונה של פרמטרים תייצר את ההסתברויות על כל מחלקה. אנו יכולים להשתמש dist.sample_distributions להשיג בחלוקה הסופית במודל.

def classifier_probs(params):
  dists, _ = dist.sample_distributions(seed=random.PRNGKey(0),
                                       value=params + (None,))
  return dists[-1].distribution.probs_parameter()

אנחנו יכולים vmap(classifier_probs) מעל לקבוצת דגימות כדי לקבל את ההסתברויות הכיתה החזוי עבור כל הדגימות שלנו. לאחר מכן אנו מחשבים את הדיוק הממוצע על פני כל מדגם, ואת הדיוק מממוצע מודל בייסיאני.

all_probs = jit(vmap(classifier_probs))(states)
print('Average accuracy:', jnp.mean(all_probs.argmax(axis=-1) == labels))
print('BMA accuracy:', jnp.mean(all_probs.mean(axis=0).argmax(axis=-1) == labels))

Average accuracy: 0.96952
BMA accuracy: 0.97999996

נראה ש-BMA מפחית את שיעור השגיאות שלנו בכמעט שליש!

יסודות

יש הפריון הכולל על JAX ב- API זהה TF שם במקום לקבל חפצים TF כמו tf.Tensor זה שהיא מקבלת את אנלוגי JAX. לדוגמה, בכל מקום בו tf.Tensor שימש בעבר כקלט, ה- API עכשיו צופה JAX DeviceArray . במקום להחזיר tf.Tensor , שיטות פריון כוללות תחזורנה DeviceArray ים. פריון הכולל על JAX גם עובד עם מבנים מקוננים של חפצי JAX, כמו רשימה או מילון של DeviceArray ים.

הפצות

רוב ההפצות של TFP נתמכות ב-JAX עם סמנטיקה דומה מאוד למקביליהם ל-TF. הם גם רשום JAX Pytrees , כך שהם יכולים להיות תשומות ותפוקות של פונקציות-טרנספורמציה JAX.

הפצות בסיסיות

log_prob שיטת הפצות עובדת אותו הדבר.

dist = tfd.Normal(0., 1.)
print(dist.log_prob(0.))

-0.9189385

דגימה מתוך חלוקה מחייבת עובר במפורש בתוך PRNGKey (או רשימה של מספרים שלמים) כמו seed טיעון מילות מפתח. אי העברה מפורשת של זרע יזרוק שגיאה.

tfd.Normal(0., 1.).sample(seed=random.PRNGKey(0))

DeviceArray(-0.20584226, dtype=float32)

הסמנטיקה צורה עבור הפצות נשאר אותו הדבר ב JAX, שבו הפצות יצטרך אחד מהם מהווה event_shape וכן batch_shape וציור דגימות רבות יוסיף נוספים sample_shape ממדים.

לדוגמה, tfd.MultivariateNormalDiag עם פרמטרי וקטור יהיה צורת אירוע וקטור וצורה יצווה ריקה.

dist = tfd.MultivariateNormalDiag(
    loc=jnp.zeros(5),
    scale_diag=jnp.ones(5)
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)

Event shape: (5,)
Batch shape: ()

מצד השני, tfd.Normal להם פרמטרים עם וקטורים תהיה יצווה וקטור וצורת אירוע סקלר צורה.

dist = tfd.Normal(
    loc=jnp.ones(5),
    scale=jnp.ones(5),
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)

Event shape: ()
Batch shape: (5,)

הסמנטיקה של לקיחת log_prob של דגימות עובדת זהה JAX מדי.

dist =  tfd.Normal(jnp.zeros(5), jnp.ones(5))
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)

dist =  tfd.Independent(tfd.Normal(jnp.zeros(5), jnp.ones(5)), 1)
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)

(10, 2, 5)
(10, 2)

מכיוון JAX DeviceArray הים תואם ספריות כמו numpy ו Matplotlib, נוכל להאכיל דגימות ישירות לתוך פונקציה זוממת.

sns.distplot(tfd.Normal(0., 1.).sample(1000, seed=random.PRNGKey(0)))
plt.show()

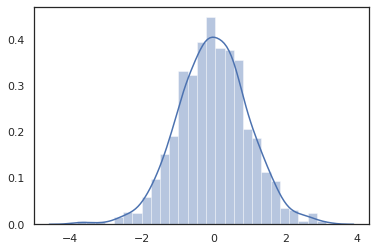
Distribution שיטות תואמות טרנספורמציות JAX.

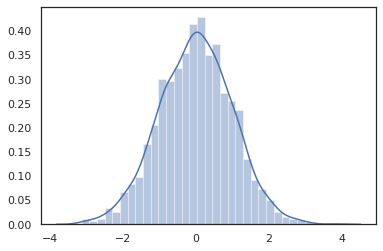
sns.distplot(jit(vmap(lambda key: tfd.Normal(0., 1.).sample(seed=key)))(
    random.split(random.PRNGKey(0), 2000)))
plt.show()

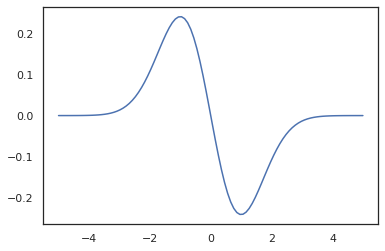
x = jnp.linspace(-5., 5., 100)
plt.plot(x, jit(vmap(grad(tfd.Normal(0., 1.).prob)))(x))
plt.show()

מכיוון הפצות TFP רשומים צמתים pytree JAX, אנחנו יכולים לכתוב פונקציות עם הפצות כמו תשומות או פלטי ולהפוך אותם באמצעות jit , אך הם עדיין אינם נתמכים טיעונים כדי vmap פונקציות -ed.

@jit
def random_distribution(key):
  loc_key, scale_key = random.split(key)
  loc, log_scale = random.normal(loc_key), random.normal(scale_key)
  return tfd.Normal(loc, jnp.exp(log_scale))
random_dist = random_distribution(random.PRNGKey(0))
print(random_dist.mean(), random_dist.variance())

0.14389051 0.081832744

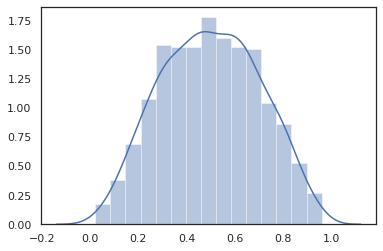
הפצות שעברו שינוי

הפצות שינו כלומר הפצות דגימות אשר מועברים באמצעות Bijector גם לעבוד מחוץ לקופסה (bijectors לעבוד מדי! ראו בהמשך).

dist = tfd.TransformedDistribution(
    tfd.Normal(0., 1.),
    tfb.Sigmoid()
)
sns.distplot(dist.sample(1000, seed=random.PRNGKey(0)))
plt.show()

חלוקות משותפות

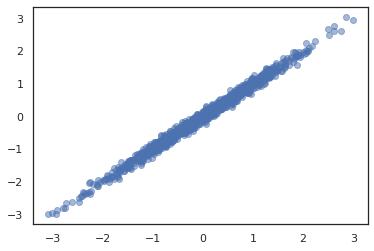
פריון כולל מציע JointDistribution ים כדי לאפשר שילוב הפצות רכיב לתוך הפצה אחת מעל משתנים אקראיים מרובים. נכון לעכשיו, הצעות הפריון הכולל שלוש גרסאות הליבה ( JointDistributionSequential , JointDistributionNamed , ו JointDistributionCoroutine ) שכולן נתמכות JAX. AutoBatched וריאנטים הם גם כל נתמך.

dist = tfd.JointDistributionSequential([
  tfd.Normal(0., 1.),
  lambda x: tfd.Normal(x, 1e-1)
])
plt.scatter(*dist.sample(1000, seed=random.PRNGKey(0)), alpha=0.5)
plt.show()

joint = tfd.JointDistributionNamed(dict(
    e=             tfd.Exponential(rate=1.),
    n=             tfd.Normal(loc=0., scale=2.),
    m=lambda n, e: tfd.Normal(loc=n, scale=e),
    x=lambda    m: tfd.Sample(tfd.Bernoulli(logits=m), 12),
))
joint.sample(seed=random.PRNGKey(0))

{'e': DeviceArray(3.376818, dtype=float32),
 'm': DeviceArray(2.5449684, dtype=float32),
 'n': DeviceArray(-0.6027825, dtype=float32),
 'x': DeviceArray([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int32)}

Root = tfd.JointDistributionCoroutine.Root
def model():
  e = yield Root(tfd.Exponential(rate=1.))
  n = yield Root(tfd.Normal(loc=0, scale=2.))
  m = yield tfd.Normal(loc=n, scale=e)
  x = yield tfd.Sample(tfd.Bernoulli(logits=m), 12)

joint = tfd.JointDistributionCoroutine(model)

joint.sample(seed=random.PRNGKey(0))

StructTuple(var0=DeviceArray(0.17315261, dtype=float32), var1=DeviceArray(-3.290489, dtype=float32), var2=DeviceArray(-3.1949058, dtype=float32), var3=DeviceArray([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], dtype=int32))

הפצות אחרות

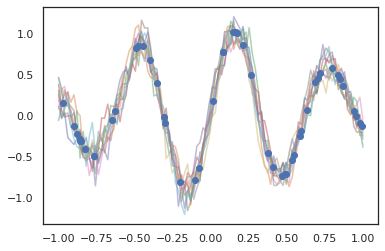
תהליכי גאוס עובדים גם במצב JAX!

k1, k2, k3 = random.split(random.PRNGKey(0), 3)
observation_noise_variance = 0.01
f = lambda x: jnp.sin(10*x[..., 0]) * jnp.exp(-x[..., 0]**2)
observation_index_points = random.uniform(
    k1, [50], minval=-1.,maxval= 1.)[..., jnp.newaxis]
observations = f(observation_index_points) + tfd.Normal(
    loc=0., scale=jnp.sqrt(observation_noise_variance)).sample(seed=k2)

index_points = jnp.linspace(-1., 1., 100)[..., jnp.newaxis]

kernel = tfpk.ExponentiatedQuadratic(length_scale=0.1)

gprm = tfd.GaussianProcessRegressionModel(
    kernel=kernel,
    index_points=index_points,
    observation_index_points=observation_index_points,
    observations=observations,
    observation_noise_variance=observation_noise_variance)

samples = gprm.sample(10, seed=k3)
for i in range(10):
  plt.plot(index_points, samples[i], alpha=0.5)
plt.plot(observation_index_points, observations, marker='o', linestyle='')
plt.show()

דגמי Markov מוסתרים נתמכים גם הם.

initial_distribution = tfd.Categorical(probs=[0.8, 0.2])
transition_distribution = tfd.Categorical(probs=[[0.7, 0.3],
                                                 [0.2, 0.8]])

observation_distribution = tfd.Normal(loc=[0., 15.], scale=[5., 10.])

model = tfd.HiddenMarkovModel(
    initial_distribution=initial_distribution,
    transition_distribution=transition_distribution,
    observation_distribution=observation_distribution,
    num_steps=7)

print(model.mean())
print(model.log_prob(jnp.zeros(7)))
print(model.sample(seed=random.PRNGKey(0)))

[3.       6.       7.5      8.249999 8.625001 8.812501 8.90625 ]
/usr/local/lib/python3.6/dist-packages/tensorflow_probability/substrates/jax/distributions/hidden_markov_model.py:483: UserWarning: HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug in which the transition model was applied prior to the initial step. This bug has been fixed. You may observe a slight change in behavior.
  'HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug '
-19.855635
[ 1.3641367  0.505798   1.3626463  3.6541772  2.272286  15.10309
 22.794212 ]

כמה הפצות כמו PixelCNN עדיין לא נתמכים בשל תלות קפדנית על תאימויות TensorFlow או XLA.

ביקטורים

רוב הביקטורים של TFP נתמכים ב-JAX היום!

tfb.Exp().inverse(1.)

DeviceArray(0., dtype=float32)

bij = tfb.Shift(1.)(tfb.Scale(3.))
print(bij.forward(jnp.ones(5)))
print(bij.inverse(jnp.ones(5)))

[4. 4. 4. 4. 4.]
[0. 0. 0. 0. 0.]

b = tfb.FillScaleTriL(diag_bijector=tfb.Exp(), diag_shift=None)
print(b.forward(x=[0., 0., 0.]))
print(b.inverse(y=[[1., 0], [.5, 2]]))

[[1. 0.]
 [0. 1.]]
[0.6931472 0.5       0.       ]

b = tfb.Chain([tfb.Exp(), tfb.Softplus()])
# or:
# b = tfb.Exp()(tfb.Softplus())
print(b.forward(-jnp.ones(5)))

[1.3678794 1.3678794 1.3678794 1.3678794 1.3678794]

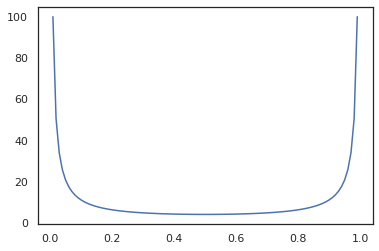
Bijectors תואמים טרנספורמציות JAX כמו jit , grad ו vmap .

jit(vmap(tfb.Exp().inverse))(jnp.arange(4.))

DeviceArray([     -inf, 0.       , 0.6931472, 1.0986123], dtype=float32)

x = jnp.linspace(0., 1., 100)
plt.plot(x, jit(grad(lambda x: vmap(tfb.Sigmoid().inverse)(x).sum()))(x))
plt.show()

Bijectors חלק, כמו RealNVP ו FFJORD עדיין אינן נתמכות.

MCMC

אנחנו ניידת את tfp.mcmc כדי JAX גם, כדי שנוכל להפעיל אלגוריתמים כמו והמילטון מונטה קרלו (HMC) ואת לא-U-Turn סמפלר (אגוזים) ב JAX.

target_log_prob = tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)).log_prob

בניגוד הפריון הכולל על TF, אנו נדרשים להעביר PRNGKey לתוך sample_chain באמצעות seed טיעון מילות מפתח.

def run_chain(key, state):
  kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-1)
  return tfp.mcmc.sample_chain(1000,
      current_state=state,
      kernel=kernel,
      trace_fn=lambda _, results: results.target_log_prob,
      seed=key)
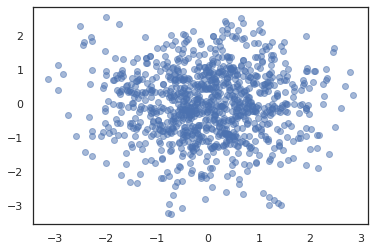
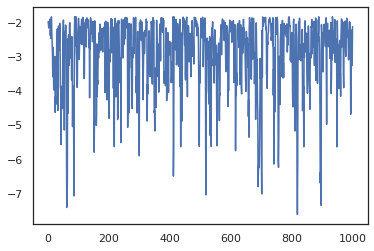
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros(2))
plt.figure()
plt.scatter(*states.T, alpha=0.5)
plt.figure()
plt.plot(log_probs)
plt.show()

כדי להפעיל רשתות מרובות, או שאנחנו יכולים לעבור קבוצה של מדינות לתוך sample_chain או שימוש vmap (למרות שאנחנו לא בחנו עדיין הבדלים בביצועים בין שתי הגישות).

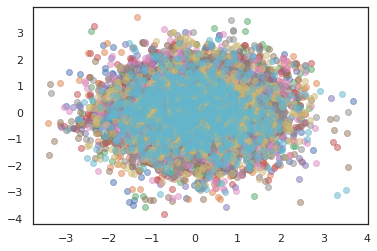
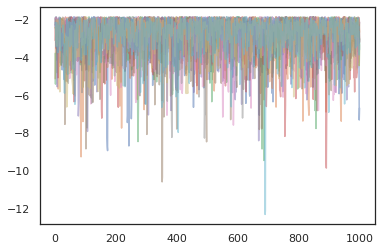
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros([10, 2]))
plt.figure()
for i in range(10):
  plt.scatter(*states[:, i].T, alpha=0.5)
plt.figure()
for i in range(10):
  plt.plot(log_probs[:, i], alpha=0.5)
plt.show()

מייעלים

TFP ב-JAX תומך בכמה מייעלים חשובים כמו BFGS ו-L-BFGS. בואו נגדיר פונקציית אובדן ריבועי בקנה מידה פשוט.

minimum = jnp.array([1.0, 1.0])  # The center of the quadratic bowl.
scales = jnp.array([2.0, 3.0])  # The scales along the two axes.

# The objective function and the gradient.
def quadratic_loss(x):
  return jnp.sum(scales * jnp.square(x - minimum))

start = jnp.array([0.6, 0.8])  # Starting point for the search.

BFGS יכול למצוא את המינימום של הפסד זה.

optim_results = tfp.optimizer.bfgs_minimize(
    value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)

# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)

Function evaluations: 5

כך גם L-BFGS יכול.

optim_results = tfp.optimizer.lbfgs_minimize(
    value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)

# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)

Function evaluations: 5

כדי vmap L-BFGS, לתת סט של למעלה פונקציה אשר מייעל את ההפסד עבור נקודת התחלה אחת.

def optimize_single(start):
  return tfp.optimizer.lbfgs_minimize(
      value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)

all_results = jit(vmap(optimize_single))(
    random.normal(random.PRNGKey(0), (10, 2)))
assert all(all_results.converged)
for i in range(10):
  np.testing.assert_allclose(optim_results.position[i], minimum)
print("Function evaluations: %s" % all_results.num_objective_evaluations)

Function evaluations: [6 6 9 6 6 8 6 8 5 9]

אזהרות

ישנם כמה הבדלים מהותיים בין TF ל-JAX, התנהגויות TFP מסוימות יהיו שונות בין שני המצעים ולא כל הפונקציונליות נתמכת. לדוגמה,

• הפריון הכולל על JAX אינו תומך דבר כזה tf.Variable מאז דבר כזה קיים JAX. זה גם אומר כלי עזר כמו tfp.util.TransformedVariable אינו נתמך גם.
• tfp.layers אינה נתמכת ב backend עדיין, בשל תלותה Keras ו tf.Variable ים.
• tfp.math.minimize לא עובד הפריון הכולל על JAX בגלל תלותה tf.Variable .
• עם TFP ב-JAX, צורות טנזור הן תמיד ערכים שלמים קונקרטיים ולעולם אינן לא ידועות/דינמיות כמו ב-TFP ב-TF.
• פסאודורנדומליות מטופלת בצורה שונה ב-TF וב-JAX (ראה נספח).
• ספריות ב tfp.experimental אינן מובטחות להתקיים המצע JAX.
• כללי קידום Dtype שונים בין TF ל-JAX. TFP ב-JAX מנסה לכבד את סמנטיקה dtype של TF באופן פנימי, לצורך עקביות.
• ביזקטורים עדיין לא נרשמו כ-JAX pytrees.

כדי לראות את הרשימה המלאה של מה נתמך הפריון הכולל על JAX, עיין בתיעוד API .

סיכום

העברנו הרבה מהתכונות של TFP ל-JAX ונשמח לראות מה כולם יבנו. חלק מהפונקציונליות עדיין לא נתמכת; אם פספסנו משהו חשוב לך (או אם אתה מוצא באג!) בבקשה להגיע אלינו - אתה יכול לשלוח tfprobability@tensorflow.org או להגיש בעיה על ריפו Github שלנו .

נספח: פסאודורנדומליות ב-JAX

דור מספר פסוודו של JAX (PRNG) המודל הוא חסר מדינה. שלא כמו מודל ממלכתי, אין מצב גלובלי בר שינוי שמתפתח לאחר כל הגרלה אקראית. במודל של JAX, אנחנו מתחילים עם מפתח PRNG, אשר פועלת כמו זוג מספרים שלמים 32 סיביות. אנחנו יכולים לבנות את המפתחות האלה באמצעות jax.random.PRNGKey .

key = random.PRNGKey(0)  # Creates a key with value [0, 0]
print(key)

[0 0]

פונקציות אקראיות ב JAX לצרוך מפתח לייצר משתנים אקראיים deterministically, כלומר הם לא צריכים לשמש שוב. לדוגמה, אנו יכולים להשתמש key לדגום ערך מתפלג נורמלית, אבל אנחנו לא צריכים להשתמש key שוב במקום אחר. יתר על כן, עובר אותו הערך לתוך random.normal ייצר אותו הערך.

print(random.normal(key))

-0.20584226

אז איך נצייר אי פעם מספר דוגמאות ממפתח אחד? התשובה היא פיצול מפתח. הרעיון הבסיסי הוא שאנחנו יכולים לפצל PRNGKey לתוך מרובים, וכל אחד המפתחות החדש יכול להתייחס אליהם כאל מקור עצמאי של אקראיות.

key1, key2 = random.split(key, num=2)
print(key1, key2)

[4146024105  967050713] [2718843009 1272950319]

פיצול מפתח הוא דטרמיניסטי אך הוא כאוטי, כך שכעת ניתן להשתמש בכל מפתח חדש כדי לצייר מדגם אקראי מובהק.

print(random.normal(key1), random.normal(key2))

0.14389051 -1.2515389

לפרטים נוספים אודות מודל פיצול מפתח הדטרמיניסטי של JAX, לראות את המדריך הזה .