 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Tensorflow Probabilité (TFP) est une bibliothèque pour le raisonnement probabiliste et l' analyse statistique qui fonctionne également sur JAX ! Pour ceux qui ne sont pas familiers, JAX est une bibliothèque de calcul numérique accéléré basée sur des transformations de fonctions composables.
TFP sur JAX prend en charge de nombreuses fonctionnalités les plus utiles de TFP standard tout en préservant les abstractions et les API avec lesquelles de nombreux utilisateurs de TFP sont désormais à l'aise.
Installer
TFP sur JAX ne dépend pas de tensorflow; désinstallons entièrement TensorFlow de ce Colab.
pip uninstall tensorflow -y -q
Nous pouvons installer TFP sur JAX avec les dernières versions nocturnes de TFP.
pip install -Uq tfp-nightly[jax] > /dev/null
Importons quelques bibliothèques Python utiles.
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn import datasets
sns.set(style='white')
/usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead. import pandas.util.testing as tm
Importons également quelques fonctionnalités JAX de base.
import jax.numpy as jnp
from jax import grad
from jax import jit
from jax import random
from jax import value_and_grad
from jax import vmap
Importation de TFP sur JAX
Pour utiliser TFP sur JAX, il suffit d' importer le jax « substrat » et l' utiliser comme vous le feriez habituellement tfp :
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
tfpk = tfp.math.psd_kernels
Démo : Régression logistique bayésienne
Pour démontrer ce que nous pouvons faire avec le backend JAX, nous allons implémenter une régression logistique bayésienne appliquée à l'ensemble de données Iris classique.
Tout d'abord, importons l'ensemble de données Iris et extrayons quelques métadonnées.
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
Nous pouvons définir le modèle en utilisant tfd.JointDistributionCoroutine . Nous allons mettre prieurs normale standard sur les poids et le terme de polarisation , puis écrire une target_log_prob fonction que les broches étiquettes échantillonnées aux données.
Root = tfd.JointDistributionCoroutine.Root
def model():
w = yield Root(tfd.Sample(tfd.Normal(0., 1.),
sample_shape=(num_features, num_classes)))
b = yield Root(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(num_classes,)))
logits = jnp.dot(features, w) + b
yield tfd.Independent(tfd.Categorical(logits=logits),
reinterpreted_batch_ndims=1)
dist = tfd.JointDistributionCoroutine(model)
def target_log_prob(*params):
return dist.log_prob(params + (labels,))
Nous prélevons de dist pour produire un état initial pour MCMC. Nous pouvons alors définir une fonction qui prend une clé aléatoire et un état initial, et produit 500 échantillons à partir d'un No-U-Turn-Sampler (NUTS). Notez que nous pouvons utiliser des transformations JAX comme jit compiler notre NUTS sampler en utilisant XLA.
init_key, sample_key = random.split(random.PRNGKey(0))
init_params = tuple(dist.sample(seed=init_key)[:-1])
@jit
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-3)
return tfp.mcmc.sample_chain(500,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
num_burnin_steps=500,
seed=key)
states, log_probs = run_chain(sample_key, init_params)
plt.figure()
plt.plot(log_probs)
plt.ylabel('Target Log Prob')
plt.xlabel('Iterations of NUTS')
plt.show()
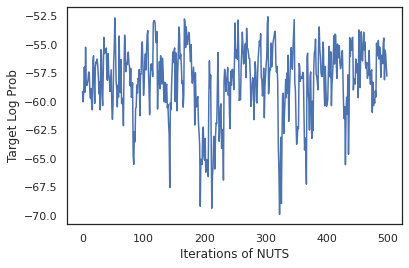
Utilisons nos échantillons pour effectuer une moyenne du modèle bayésien (BMA) en faisant la moyenne des probabilités prédites de chaque ensemble de poids.
Écrivons d'abord une fonction qui, pour un ensemble donné de paramètres, produira les probabilités sur chaque classe. Nous pouvons utiliser dist.sample_distributions pour obtenir la distribution finale dans le modèle.
def classifier_probs(params):
dists, _ = dist.sample_distributions(seed=random.PRNGKey(0),
value=params + (None,))
return dists[-1].distribution.probs_parameter()
Nous pouvons vmap(classifier_probs) sur l'ensemble des échantillons pour obtenir les probabilités de classe prévues pour chacun de nos échantillons. Nous calculons ensuite la précision moyenne sur chaque échantillon et la précision à partir de la moyenne du modèle bayésien.
all_probs = jit(vmap(classifier_probs))(states)
print('Average accuracy:', jnp.mean(all_probs.argmax(axis=-1) == labels))
print('BMA accuracy:', jnp.mean(all_probs.mean(axis=0).argmax(axis=-1) == labels))
Average accuracy: 0.96952 BMA accuracy: 0.97999996
On dirait que BMA réduit notre taux d'erreur de près d'un tiers !
Fondamentaux
TFP sur JAX a une API identique à TF où au lieu d'accepter des objets TF comme tf.Tensor s il accepte l'analogue de JAX. Par exemple, chaque fois qu'un tf.Tensor était auparavant utilisé comme entrée, l'API attend maintenant un JAX DeviceArray . Au lieu de retourner un tf.Tensor , les méthodes TFP retourneront DeviceArray s. TFP sur JAX travaille également avec des structures imbriquées d'objets JAX, comme une liste ou un dictionnaire de DeviceArray s.
Répartition
La plupart des distributions de TFP sont supportées en JAX avec une sémantique très similaire à leurs homologues de TF. Ils sont également inscrits comme JAX Pytrees , afin qu'ils puissent être entrées et sorties des fonctions transformées JAX.
Répartitions de base
La log_prob méthode de distribution fonctionne de la même.
dist = tfd.Normal(0., 1.)
print(dist.log_prob(0.))
-0.9189385
L' échantillonnage d'une distribution nécessite le passage explicitement dans une PRNGKey (ou une liste d'entiers) comme seed argument mot - clé. Ne pas transmettre explicitement une graine générera une erreur.
tfd.Normal(0., 1.).sample(seed=random.PRNGKey(0))
DeviceArray(-0.20584226, dtype=float32)
La sémantique de forme pour les distributions restent les mêmes dans JAX, où les distributions auront chacun un event_shape et un batch_shape et dessin de nombreux échantillons ajoutera supplémentaires sample_shape dimensions.
Par exemple, un tfd.MultivariateNormalDiag avec des paramètres de vecteur aura une forme d'événement vecteur et la forme de lot vide.
dist = tfd.MultivariateNormalDiag(
loc=jnp.zeros(5),
scale_diag=jnp.ones(5)
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: (5,) Batch shape: ()
D'autre part, un tfd.Normal paramétrés avec des vecteurs aura une forme d'événement scalaire et vecteur forme lot.
dist = tfd.Normal(
loc=jnp.ones(5),
scale=jnp.ones(5),
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: () Batch shape: (5,)
La sémantique de la prise log_prob des échantillons fonctionne de la même dans JAX aussi.
dist = tfd.Normal(jnp.zeros(5), jnp.ones(5))
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
dist = tfd.Independent(tfd.Normal(jnp.zeros(5), jnp.ones(5)), 1)
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
(10, 2, 5) (10, 2)
Parce que JAX DeviceArray s sont compatibles avec les bibliothèques comme NumPy et Matplotlib, nous pouvons nourrir des échantillons directement dans une fonction de traçage.
sns.distplot(tfd.Normal(0., 1.).sample(1000, seed=random.PRNGKey(0)))
plt.show()
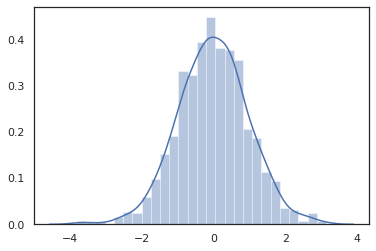
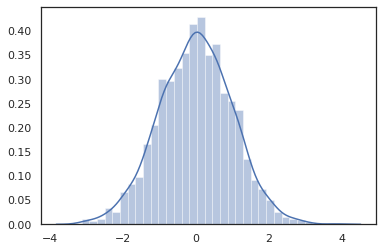
Distribution méthodes sont compatibles avec les transformations de JAX.
sns.distplot(jit(vmap(lambda key: tfd.Normal(0., 1.).sample(seed=key)))(
random.split(random.PRNGKey(0), 2000)))
plt.show()
x = jnp.linspace(-5., 5., 100)
plt.plot(x, jit(vmap(grad(tfd.Normal(0., 1.).prob)))(x))
plt.show()
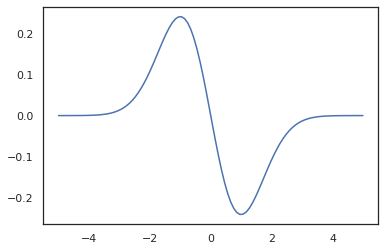
Parce que les distributions TFP sont enregistrées en tant que JAX nœuds de pytree, nous pouvons écrire des fonctions avec des distributions comme entrées ou sorties et de les transformer en utilisant jit , mais ils ne sont pas encore pris en charge comme arguments pour vmap fonctions -ed.
@jit
def random_distribution(key):
loc_key, scale_key = random.split(key)
loc, log_scale = random.normal(loc_key), random.normal(scale_key)
return tfd.Normal(loc, jnp.exp(log_scale))
random_dist = random_distribution(random.PRNGKey(0))
print(random_dist.mean(), random_dist.variance())
0.14389051 0.081832744
Distributions transformées
Distributions distributions dont Transformé -à- dire les échantillons sont passés à travers un Bijector travaillent également hors de la boîte (bijectors trop de travail! Voir ci - dessous).
dist = tfd.TransformedDistribution(
tfd.Normal(0., 1.),
tfb.Sigmoid()
)
sns.distplot(dist.sample(1000, seed=random.PRNGKey(0)))
plt.show()
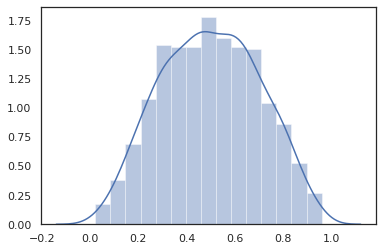
Distributions conjointes
TFP offre JointDistribution s pour permettre la combinaison des distributions de composants dans une distribution unique sur plusieurs variables aléatoires. À l' heure actuelle, TFP propose trois variantes de base ( JointDistributionSequential , JointDistributionNamed et JointDistributionCoroutine ) qui sont tous pris en charge par JAX. Les AutoBatched variantes sont tous pris en charge.
dist = tfd.JointDistributionSequential([
tfd.Normal(0., 1.),
lambda x: tfd.Normal(x, 1e-1)
])
plt.scatter(*dist.sample(1000, seed=random.PRNGKey(0)), alpha=0.5)
plt.show()
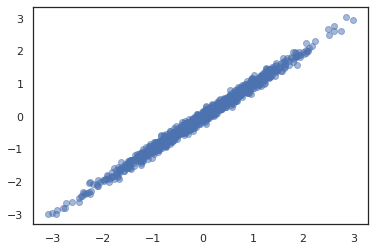
joint = tfd.JointDistributionNamed(dict(
e= tfd.Exponential(rate=1.),
n= tfd.Normal(loc=0., scale=2.),
m=lambda n, e: tfd.Normal(loc=n, scale=e),
x=lambda m: tfd.Sample(tfd.Bernoulli(logits=m), 12),
))
joint.sample(seed=random.PRNGKey(0))
{'e': DeviceArray(3.376818, dtype=float32),
'm': DeviceArray(2.5449684, dtype=float32),
'n': DeviceArray(-0.6027825, dtype=float32),
'x': DeviceArray([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int32)}
Root = tfd.JointDistributionCoroutine.Root
def model():
e = yield Root(tfd.Exponential(rate=1.))
n = yield Root(tfd.Normal(loc=0, scale=2.))
m = yield tfd.Normal(loc=n, scale=e)
x = yield tfd.Sample(tfd.Bernoulli(logits=m), 12)
joint = tfd.JointDistributionCoroutine(model)
joint.sample(seed=random.PRNGKey(0))
StructTuple(var0=DeviceArray(0.17315261, dtype=float32), var1=DeviceArray(-3.290489, dtype=float32), var2=DeviceArray(-3.1949058, dtype=float32), var3=DeviceArray([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], dtype=int32))
Autres répartitions
Les processus gaussiens fonctionnent également en mode JAX !
k1, k2, k3 = random.split(random.PRNGKey(0), 3)
observation_noise_variance = 0.01
f = lambda x: jnp.sin(10*x[..., 0]) * jnp.exp(-x[..., 0]**2)
observation_index_points = random.uniform(
k1, [50], minval=-1.,maxval= 1.)[..., jnp.newaxis]
observations = f(observation_index_points) + tfd.Normal(
loc=0., scale=jnp.sqrt(observation_noise_variance)).sample(seed=k2)
index_points = jnp.linspace(-1., 1., 100)[..., jnp.newaxis]
kernel = tfpk.ExponentiatedQuadratic(length_scale=0.1)
gprm = tfd.GaussianProcessRegressionModel(
kernel=kernel,
index_points=index_points,
observation_index_points=observation_index_points,
observations=observations,
observation_noise_variance=observation_noise_variance)
samples = gprm.sample(10, seed=k3)
for i in range(10):
plt.plot(index_points, samples[i], alpha=0.5)
plt.plot(observation_index_points, observations, marker='o', linestyle='')
plt.show()
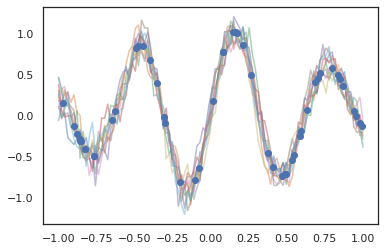
Les modèles de Markov cachés sont également pris en charge.
initial_distribution = tfd.Categorical(probs=[0.8, 0.2])
transition_distribution = tfd.Categorical(probs=[[0.7, 0.3],
[0.2, 0.8]])
observation_distribution = tfd.Normal(loc=[0., 15.], scale=[5., 10.])
model = tfd.HiddenMarkovModel(
initial_distribution=initial_distribution,
transition_distribution=transition_distribution,
observation_distribution=observation_distribution,
num_steps=7)
print(model.mean())
print(model.log_prob(jnp.zeros(7)))
print(model.sample(seed=random.PRNGKey(0)))
[3. 6. 7.5 8.249999 8.625001 8.812501 8.90625 ] /usr/local/lib/python3.6/dist-packages/tensorflow_probability/substrates/jax/distributions/hidden_markov_model.py:483: UserWarning: HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug in which the transition model was applied prior to the initial step. This bug has been fixed. You may observe a slight change in behavior. 'HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug ' -19.855635 [ 1.3641367 0.505798 1.3626463 3.6541772 2.272286 15.10309 22.794212 ]
Quelques distributions comme PixelCNN ne sont pas encore pris en charge en raison de dépendances strictes sur les incompatibilités tensorflow ou XLA.
Bijecteurs
La plupart des bijecteurs de TFP sont supportés en JAX aujourd'hui !
tfb.Exp().inverse(1.)
DeviceArray(0., dtype=float32)
bij = tfb.Shift(1.)(tfb.Scale(3.))
print(bij.forward(jnp.ones(5)))
print(bij.inverse(jnp.ones(5)))
[4. 4. 4. 4. 4.] [0. 0. 0. 0. 0.]
b = tfb.FillScaleTriL(diag_bijector=tfb.Exp(), diag_shift=None)
print(b.forward(x=[0., 0., 0.]))
print(b.inverse(y=[[1., 0], [.5, 2]]))
[[1. 0.] [0. 1.]] [0.6931472 0.5 0. ]
b = tfb.Chain([tfb.Exp(), tfb.Softplus()])
# or:
# b = tfb.Exp()(tfb.Softplus())
print(b.forward(-jnp.ones(5)))
[1.3678794 1.3678794 1.3678794 1.3678794 1.3678794]
Bijectors sont compatibles avec les transformations de JAX comme jit , grad et vmap .
jit(vmap(tfb.Exp().inverse))(jnp.arange(4.))
DeviceArray([ -inf, 0. , 0.6931472, 1.0986123], dtype=float32)
x = jnp.linspace(0., 1., 100)
plt.plot(x, jit(grad(lambda x: vmap(tfb.Sigmoid().inverse)(x).sum()))(x))
plt.show()
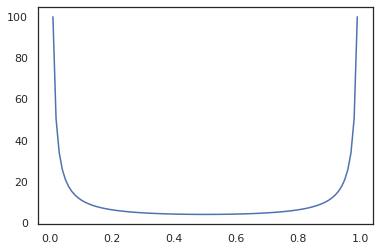
Certains bijectors, comme RealNVP et FFJORD ne sont pas encore pris en charge.
MCMC
Nous avons porté tfp.mcmc à JAX aussi bien, afin que nous puissions exécuter des algorithmes comme hamiltonien Monte Carlo (HMC) et le No-U-Turn-Sampler (NUTS) en JAX.
target_log_prob = tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)).log_prob
Contrairement à TFP sur TF, nous sommes tenus de passer un PRNGKey en sample_chain en utilisant la seed argument mot - clé.
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-1)
return tfp.mcmc.sample_chain(1000,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
seed=key)
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros(2))
plt.figure()
plt.scatter(*states.T, alpha=0.5)
plt.figure()
plt.plot(log_probs)
plt.show()
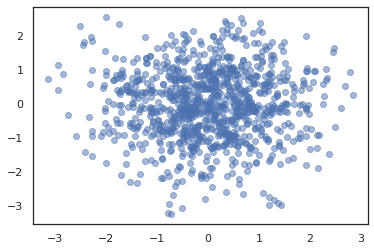
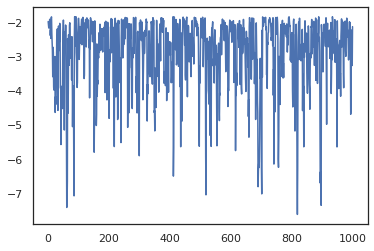
Pour exécuter plusieurs chaînes, nous pouvons soit passer un lot d'états dans sample_chain ou l' utilisation vmap (bien que nous n'avons pas encore exploré les différences de performance entre les deux approches).
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros([10, 2]))
plt.figure()
for i in range(10):
plt.scatter(*states[:, i].T, alpha=0.5)
plt.figure()
for i in range(10):
plt.plot(log_probs[:, i], alpha=0.5)
plt.show()
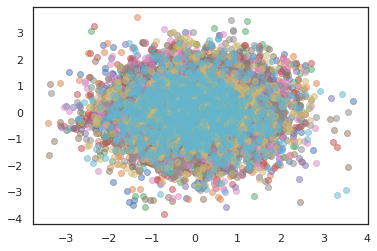
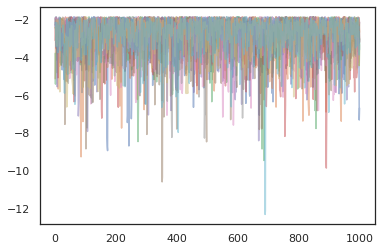
Optimiseurs
TFP sur JAX prend en charge certains optimiseurs importants tels que BFGS et L-BFGS. Mettons en place une simple fonction de perte quadratique mise à l'échelle.
minimum = jnp.array([1.0, 1.0]) # The center of the quadratic bowl.
scales = jnp.array([2.0, 3.0]) # The scales along the two axes.
# The objective function and the gradient.
def quadratic_loss(x):
return jnp.sum(scales * jnp.square(x - minimum))
start = jnp.array([0.6, 0.8]) # Starting point for the search.
BFGS peut trouver le minimum de cette perte.
optim_results = tfp.optimizer.bfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
Le L-BFGS aussi.
optim_results = tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
Pour vmap L-BFGS, Fixons une fonction qui permet d' optimiser la perte d'un seul point de départ.
def optimize_single(start):
return tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
all_results = jit(vmap(optimize_single))(
random.normal(random.PRNGKey(0), (10, 2)))
assert all(all_results.converged)
for i in range(10):
np.testing.assert_allclose(optim_results.position[i], minimum)
print("Function evaluations: %s" % all_results.num_objective_evaluations)
Function evaluations: [6 6 9 6 6 8 6 8 5 9]
Mises en garde
Il existe des différences fondamentales entre TF et JAX, certains comportements TFP seront différents entre les deux substrats et toutes les fonctionnalités ne sont pas prises en charge. Par example,
- TFP sur JAX ne supporte pas quelque chose comme
tf.Variablepuisque rien comme il existe dans JAX. Cela signifie également des utilitaires commetfp.util.TransformedVariablene sont pas pris en charge non plus . -
tfp.layersest pas pris en charge dans le back - end encore, en raison de sa dépendance à l' égard Keras ettf.Variables. -
tfp.math.minimizene fonctionne pas dans le TFP JAX en raison de sa dépendance à l' égardtf.Variable. - Avec TFP sur JAX, les formes tensorielles sont toujours des valeurs entières concrètes et ne sont jamais inconnues/dynamiques comme dans TFP sur TF.
- Le pseudo-aléatoire est géré différemment dans TF et JAX (voir annexe).
- Les bibliothèques de
tfp.experimentalne sont pas garantis d'exister dans le substrat JAX. - Les règles de promotion Dtype sont différentes entre TF et JAX. TFP sur JAX essaie de respecter la sémantique dtype de TF en interne, par souci de cohérence.
- Les bijecteurs n'ont pas encore été enregistrés en tant que pytrees JAX.
Pour voir la liste complète de ce qui est pris en charge dans TFP sur JAX, s'il vous plaît se référer à la documentation de l' API .
Conclusion
Nous avons porté de nombreuses fonctionnalités de TFP sur JAX et sommes impatients de voir ce que tout le monde va construire. Certaines fonctionnalités ne sont pas encore prises en charge ; si nous avons manqué quelque chose d' important pour vous (ou si vous trouvez un bug!) s'il vous plaît nous rejoindre - vous pouvez envoyer tfprobability@tensorflow.org ou déposer une question sur notre repo Github .
Annexe : pseudo-aléatoire dans JAX
Le modèle de génération de nombres pseudo - aléatoires (PRNG) de Jax est apatride. Contrairement à un modèle avec état, il n'y a pas d'état global mutable qui évolue après chaque tirage aléatoire. Dans le modèle de JAX, nous commençons par une clé PRNG, qui agit comme une paire d'entiers 32 bits. Nous pouvons construire ces clés en utilisant jax.random.PRNGKey .
key = random.PRNGKey(0) # Creates a key with value [0, 0]
print(key)
[0 0]
Fonctions aléatoires JAX consomment une clé pour produire un nombre aléatoire déterministe, ce qui signifie qu'ils ne doivent pas être utilisés à nouveau. Par exemple, nous pouvons utiliser la key pour échantillonner une valeur distribuée normalement, mais il ne faut pas utiliser la key à nouveau ailleurs. De plus, en passant la même valeur en random.normal produira la même valeur.
print(random.normal(key))
-0.20584226
Alors, comment pouvons-nous tirer plusieurs échantillons à partir d'une seule clé ? La réponse est la scission de clé. L'idée de base est que l' on peut diviser un PRNGKey en plusieurs, et chacune des nouvelles clés peuvent être traitées comme une source indépendante de caractère aléatoire.
key1, key2 = random.split(key, num=2)
print(key1, key2)
[4146024105 967050713] [2718843009 1272950319]
Le fractionnement des clés est déterministe mais chaotique, de sorte que chaque nouvelle clé peut désormais être utilisée pour tirer un échantillon aléatoire distinct.
print(random.normal(key1), random.normal(key2))
0.14389051 -1.2515389
Pour plus de détails sur le modèle de partage de clé déterministe de JAX, consultez ce guide .
