احتمال TensorFlow در JAX

مشاهده در TensorFlow.org

در Google Colab اجرا شود

مشاهده منبع در GitHub

دانلود دفترچه یادداشت

TensorFlow احتمال (TFP) یک کتابخانه برای استدلال احتمالاتی و تجزیه و تحلیل های آماری است که در حال حاضر نیز در کار است JAX ! برای کسانی که آشنایی ندارند، JAX کتابخانه ای برای محاسبات عددی تسریع شده بر اساس تبدیل توابع قابل ترکیب است.

TFP در JAX از بسیاری از مفیدترین عملکردهای TFP معمولی پشتیبانی می کند و در عین حال انتزاعات و APIهایی را که بسیاری از کاربران TFP اکنون با آنها راحت هستند حفظ می کند.

برپایی

بهره وری کل عوامل در JAX بر روی TensorFlow بستگی ندارد؛ بیایید TensorFlow را به طور کامل از این Colab حذف کنیم.

pip uninstall tensorflow -y -q

ما می‌توانیم TFP را روی JAX با جدیدترین بیلدهای شبانه TFP نصب کنیم.

pip install -Uq tfp-nightly[jax] > /dev/null

بیایید چند کتابخانه مفید پایتون را وارد کنیم.

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn import datasets
sns.set(style='white')

/usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead.
  import pandas.util.testing as tm

اجازه دهید برخی از عملکردهای اولیه JAX را نیز وارد کنیم.

import jax.numpy as jnp
from jax import grad
from jax import jit
from jax import random
from jax import value_and_grad
from jax import vmap

وارد کردن TFP در JAX

برای استفاده از بهره وری کل عوامل در JAX، به سادگی وارد jax "بستر" و استفاده از آن به عنوان شما معمولا می tfp :

from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
tfpk = tfp.math.psd_kernels

نسخه ی نمایشی: رگرسیون لجستیک بیزی

برای نشان دادن کارهایی که می‌توانیم با باطن JAX انجام دهیم، رگرسیون لجستیک بیزی را که در مجموعه داده کلاسیک Iris اعمال می‌شود، پیاده‌سازی می‌کنیم.

ابتدا، بیایید مجموعه داده Iris را وارد کرده و برخی از متادیتا را استخراج کنیم.

iris = datasets.load_iris()
features, labels = iris['data'], iris['target']

num_features = features.shape[-1]
num_classes = len(iris.target_names)

ما می توانیم مدل با استفاده از تعریف tfd.JointDistributionCoroutine . ما priors نرمال استاندارد در هر دو وزن و مدت تعصب را قرار داده و سپس ارسال نامه target_log_prob تابع است که پین برچسب نمونه به داده ها.

Root = tfd.JointDistributionCoroutine.Root
def model():
  w = yield Root(tfd.Sample(tfd.Normal(0., 1.),
                            sample_shape=(num_features, num_classes)))
  b = yield Root(
      tfd.Sample(tfd.Normal(0., 1.), sample_shape=(num_classes,)))
  logits = jnp.dot(features, w) + b
  yield tfd.Independent(tfd.Categorical(logits=logits),
                        reinterpreted_batch_ndims=1)


dist = tfd.JointDistributionCoroutine(model)
def target_log_prob(*params):
  return dist.log_prob(params + (labels,))

ما از نمونه dist برای تولید یک حالت اولیه برای MCMC. سپس می‌توانیم تابعی را تعریف کنیم که در یک کلید تصادفی و یک حالت اولیه قرار می‌گیرد و 500 نمونه از یک نمونه‌بردار بدون چرخش (NUTS) تولید می‌کند. توجه داشته باشید که ما می توانیم تحولات JAX مانند استفاده از jit کامپایل نمونه آجیل ما با استفاده از XLA.

init_key, sample_key = random.split(random.PRNGKey(0))
init_params = tuple(dist.sample(seed=init_key)[:-1])

@jit
def run_chain(key, state):
  kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-3)
  return tfp.mcmc.sample_chain(500,
      current_state=state,
      kernel=kernel,
      trace_fn=lambda _, results: results.target_log_prob,
      num_burnin_steps=500,
      seed=key)

states, log_probs = run_chain(sample_key, init_params)
plt.figure()
plt.plot(log_probs)
plt.ylabel('Target Log Prob')
plt.xlabel('Iterations of NUTS')
plt.show()

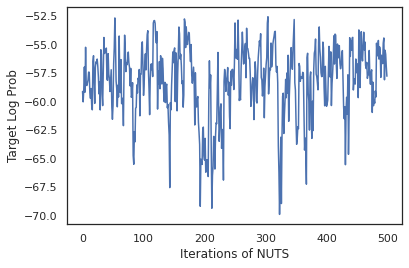
بیایید از نمونه‌های خود برای انجام میانگین‌گیری مدل بیزی (BMA) با میانگین‌گیری احتمالات پیش‌بینی‌شده هر مجموعه از وزن‌ها استفاده کنیم.

ابتدا اجازه دهید تابعی بنویسیم که برای مجموعه پارامترهای معینی احتمالات هر کلاس را تولید کند. ما می توانید استفاده کنید dist.sample_distributions برای به دست آوردن توزیع نهایی در مدل.

def classifier_probs(params):
  dists, _ = dist.sample_distributions(seed=random.PRNGKey(0),
                                       value=params + (None,))
  return dists[-1].distribution.probs_parameter()

ما می توانیم vmap(classifier_probs) بیش از مجموعه ای از نمونه برای دریافت احتمالات کلاس پیش بینی شده برای هر یک از نمونه های ما. سپس میانگین دقت در هر نمونه و دقت را از مدل بیزی به طور میانگین محاسبه می کنیم.

all_probs = jit(vmap(classifier_probs))(states)
print('Average accuracy:', jnp.mean(all_probs.argmax(axis=-1) == labels))
print('BMA accuracy:', jnp.mean(all_probs.mean(axis=0).argmax(axis=-1) == labels))

Average accuracy: 0.96952
BMA accuracy: 0.97999996

به نظر می رسد BMA میزان خطای ما را تقریباً یک سوم کاهش می دهد!

مبانی

بهره وری کل عوامل در JAX دارای یک API یکسان به TF که در آن به جای پذیرش اشیاء TF مانند tf.Tensor ها آن آنالوگ JAX می پذیرد. به عنوان مثال، در هر کجا که tf.Tensor قبلا به عنوان ورودی استفاده شده است، API در حال حاضر در انتظار یک JAX DeviceArray . به جای بازگشت tf.Tensor ، روش بهره وری کل عوامل باز خواهد گشت DeviceArray است. بهره وری کل عوامل در JAX نیز با ساختارهای تودرتو از اشیاء JAX، مانند یک لیست و یا فرهنگ لغت از کار DeviceArray است.

توزیع ها

اکثر توزیع های TFP در JAX با معنایی بسیار مشابه با همتایان TF خود پشتیبانی می شوند. آنها همچنین به عنوان ثبت نام JAX Pytrees ، به طوری که آنها می تواند ورودی و خروجی از توابع JAX-تبدیل شده است.

توزیع های پایه

log_prob روش برای توزیع همان کار می کند.

dist = tfd.Normal(0., 1.)
print(dist.log_prob(0.))

-0.9189385

نمونه برداری از یک توزیع نیاز به صراحت در عبور PRNGKey (یا لیستی از اعداد صحیح) را به عنوان seed استدلال کلمه کلیدی. عدم عبور صریح در یک دانه باعث ایجاد خطا می شود.

tfd.Normal(0., 1.).sample(seed=random.PRNGKey(0))

DeviceArray(-0.20584226, dtype=float32)

معناشناسی شکل برای توزیع در همان JAX، که در آن توزیع هر یک باقی می ماند event_shape و یک batch_shape و رسم بسیاری از نمونه ها خواهد دیگری را اضافه کنید sample_shape ابعاد.

برای مثال، یک tfd.MultivariateNormalDiag با پارامترهای بردار به شکل رویداد بردار و شکل دسته ای خالی داشته باشد.

dist = tfd.MultivariateNormalDiag(
    loc=jnp.zeros(5),
    scale_diag=jnp.ones(5)
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)

Event shape: (5,)
Batch shape: ()

از سوی دیگر، یک tfd.Normal با بردار پارامتر به شکل رویداد و دسته ای بردار شکل اسکالر است.

dist = tfd.Normal(
    loc=jnp.ones(5),
    scale=jnp.ones(5),
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)

Event shape: ()
Batch shape: (5,)

معناشناسی گرفتن log_prob از نمونه ها همان در JAX کار می کند بیش از حد.

dist =  tfd.Normal(jnp.zeros(5), jnp.ones(5))
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)

dist =  tfd.Independent(tfd.Normal(jnp.zeros(5), jnp.ones(5)), 1)
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)

(10, 2, 5)
(10, 2)

از آنجا JAX DeviceArray S سازگار با کتابخانه مانند نامپای و کتابخانه متپلات، ما می توانیم نمونه به طور مستقیم به یک تابع توطئه تغذیه می کنند.

sns.distplot(tfd.Normal(0., 1.).sample(1000, seed=random.PRNGKey(0)))
plt.show()

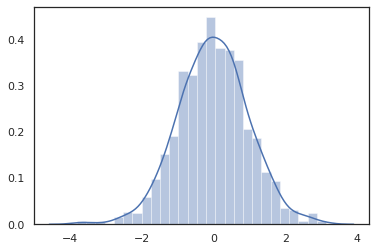
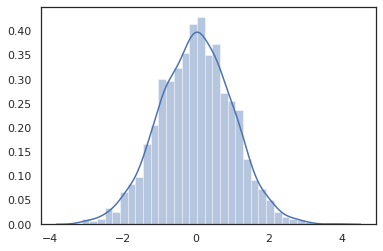
Distribution روش سازگار با تحولات JAX هستند.

sns.distplot(jit(vmap(lambda key: tfd.Normal(0., 1.).sample(seed=key)))(
    random.split(random.PRNGKey(0), 2000)))
plt.show()

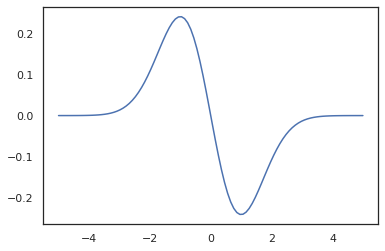
x = jnp.linspace(-5., 5., 100)
plt.plot(x, jit(vmap(grad(tfd.Normal(0., 1.).prob)))(x))
plt.show()

از آنجا که توزیع بهره وری کل عوامل به عنوان گره pytree JAX ثبت نام، ما می توانیم توابع با توزیع به عنوان ورودی یا خروجی ارسال و تبدیل آنها با استفاده از jit ، اما آنها هنوز به عنوان آرگومان به پشتیبانی نمی vmap توابع -ed.

@jit
def random_distribution(key):
  loc_key, scale_key = random.split(key)
  loc, log_scale = random.normal(loc_key), random.normal(scale_key)
  return tfd.Normal(loc, jnp.exp(log_scale))
random_dist = random_distribution(random.PRNGKey(0))
print(random_dist.mean(), random_dist.variance())

0.14389051 0.081832744

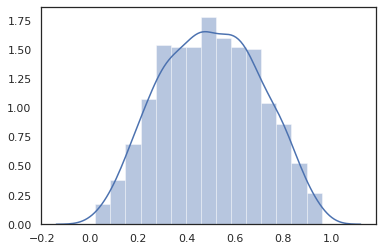
توزیع های تبدیل شده

توزیع تبدیل یعنی توزیع که نمونه آنها را از طریق یک گذشت Bijector نیز کار خارج از جعبه (bijectors کار بیش از حد! پایین را ببینید).

dist = tfd.TransformedDistribution(
    tfd.Normal(0., 1.),
    tfb.Sigmoid()
)
sns.distplot(dist.sample(1000, seed=random.PRNGKey(0)))
plt.show()

توزیع های مشترک

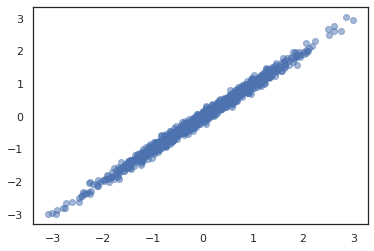
بهره وری کل عوامل ارائه می دهد JointDistribution برای فعال کردن ترکیب توزیع جزء را به یک توزیع تک بیش از متغیرهای تصادفی متعدد. در حال حاضر، بهره وری کل عوامل پیشنهادات سه مدل هسته ای ( JointDistributionSequential ، JointDistributionNamed و JointDistributionCoroutine ) که در JAX پشتیبانی می شوند. AutoBatched انواع نیز پشتیبانی می کند.

dist = tfd.JointDistributionSequential([
  tfd.Normal(0., 1.),
  lambda x: tfd.Normal(x, 1e-1)
])
plt.scatter(*dist.sample(1000, seed=random.PRNGKey(0)), alpha=0.5)
plt.show()

joint = tfd.JointDistributionNamed(dict(
    e=             tfd.Exponential(rate=1.),
    n=             tfd.Normal(loc=0., scale=2.),
    m=lambda n, e: tfd.Normal(loc=n, scale=e),
    x=lambda    m: tfd.Sample(tfd.Bernoulli(logits=m), 12),
))
joint.sample(seed=random.PRNGKey(0))

{'e': DeviceArray(3.376818, dtype=float32),
 'm': DeviceArray(2.5449684, dtype=float32),
 'n': DeviceArray(-0.6027825, dtype=float32),
 'x': DeviceArray([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int32)}

Root = tfd.JointDistributionCoroutine.Root
def model():
  e = yield Root(tfd.Exponential(rate=1.))
  n = yield Root(tfd.Normal(loc=0, scale=2.))
  m = yield tfd.Normal(loc=n, scale=e)
  x = yield tfd.Sample(tfd.Bernoulli(logits=m), 12)

joint = tfd.JointDistributionCoroutine(model)

joint.sample(seed=random.PRNGKey(0))

StructTuple(var0=DeviceArray(0.17315261, dtype=float32), var1=DeviceArray(-3.290489, dtype=float32), var2=DeviceArray(-3.1949058, dtype=float32), var3=DeviceArray([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], dtype=int32))

سایر توزیع ها

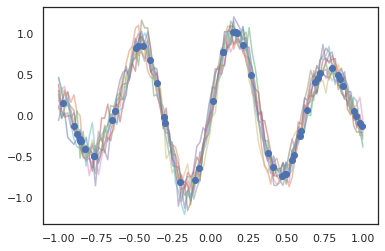
فرآیندهای گاوسی نیز در حالت JAX کار می کنند!

k1, k2, k3 = random.split(random.PRNGKey(0), 3)
observation_noise_variance = 0.01
f = lambda x: jnp.sin(10*x[..., 0]) * jnp.exp(-x[..., 0]**2)
observation_index_points = random.uniform(
    k1, [50], minval=-1.,maxval= 1.)[..., jnp.newaxis]
observations = f(observation_index_points) + tfd.Normal(
    loc=0., scale=jnp.sqrt(observation_noise_variance)).sample(seed=k2)

index_points = jnp.linspace(-1., 1., 100)[..., jnp.newaxis]

kernel = tfpk.ExponentiatedQuadratic(length_scale=0.1)

gprm = tfd.GaussianProcessRegressionModel(
    kernel=kernel,
    index_points=index_points,
    observation_index_points=observation_index_points,
    observations=observations,
    observation_noise_variance=observation_noise_variance)

samples = gprm.sample(10, seed=k3)
for i in range(10):
  plt.plot(index_points, samples[i], alpha=0.5)
plt.plot(observation_index_points, observations, marker='o', linestyle='')
plt.show()

مدل های پنهان مارکوف نیز پشتیبانی می شوند.

initial_distribution = tfd.Categorical(probs=[0.8, 0.2])
transition_distribution = tfd.Categorical(probs=[[0.7, 0.3],
                                                 [0.2, 0.8]])

observation_distribution = tfd.Normal(loc=[0., 15.], scale=[5., 10.])

model = tfd.HiddenMarkovModel(
    initial_distribution=initial_distribution,
    transition_distribution=transition_distribution,
    observation_distribution=observation_distribution,
    num_steps=7)

print(model.mean())
print(model.log_prob(jnp.zeros(7)))
print(model.sample(seed=random.PRNGKey(0)))

[3.       6.       7.5      8.249999 8.625001 8.812501 8.90625 ]
/usr/local/lib/python3.6/dist-packages/tensorflow_probability/substrates/jax/distributions/hidden_markov_model.py:483: UserWarning: HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug in which the transition model was applied prior to the initial step. This bug has been fixed. You may observe a slight change in behavior.
  'HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug '
-19.855635
[ 1.3641367  0.505798   1.3626463  3.6541772  2.272286  15.10309
 22.794212 ]

چند توزیع مانند PixelCNN به دلیل وابستگی های سخت در TensorFlow یا وابسته به جنس مورد ناسازگاری پشتیبانی نشده است.

بیژکتورها

امروزه اکثر بیژکتورهای TFP در JAX پشتیبانی می شوند!

tfb.Exp().inverse(1.)

DeviceArray(0., dtype=float32)

bij = tfb.Shift(1.)(tfb.Scale(3.))
print(bij.forward(jnp.ones(5)))
print(bij.inverse(jnp.ones(5)))

[4. 4. 4. 4. 4.]
[0. 0. 0. 0. 0.]

b = tfb.FillScaleTriL(diag_bijector=tfb.Exp(), diag_shift=None)
print(b.forward(x=[0., 0., 0.]))
print(b.inverse(y=[[1., 0], [.5, 2]]))

[[1. 0.]
 [0. 1.]]
[0.6931472 0.5       0.       ]

b = tfb.Chain([tfb.Exp(), tfb.Softplus()])
# or:
# b = tfb.Exp()(tfb.Softplus())
print(b.forward(-jnp.ones(5)))

[1.3678794 1.3678794 1.3678794 1.3678794 1.3678794]

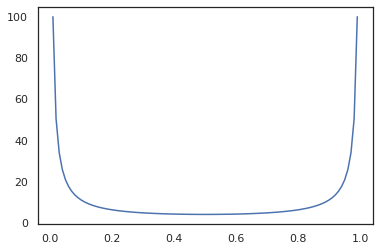
Bijectors سازگار با تحولات JAX مانند jit ، grad و vmap .

jit(vmap(tfb.Exp().inverse))(jnp.arange(4.))

DeviceArray([     -inf, 0.       , 0.6931472, 1.0986123], dtype=float32)

x = jnp.linspace(0., 1., 100)
plt.plot(x, jit(grad(lambda x: vmap(tfb.Sigmoid().inverse)(x).sum()))(x))
plt.show()

برخی bijectors، مانند RealNVP و FFJORD هنوز پشتیبانی نمی شود.

MCMC

ما باید منتقل tfp.mcmc به JAX به عنوان خوب، بنابراین ما می توانیم الگوریتم مانند هامیلتونی مونت کارلو (HMC) و بدون دوربرگردان-نمونه (آجیل) در JAX اجرا کنید.

target_log_prob = tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)).log_prob

بر خلاف بهره وری کل عوامل در TF، ما ملزم به گذراندن یک PRNGKey به sample_chain با استفاده از seed استدلال کلمه کلیدی.

def run_chain(key, state):
  kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-1)
  return tfp.mcmc.sample_chain(1000,
      current_state=state,
      kernel=kernel,
      trace_fn=lambda _, results: results.target_log_prob,
      seed=key)
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros(2))
plt.figure()
plt.scatter(*states.T, alpha=0.5)
plt.figure()
plt.plot(log_probs)
plt.show()

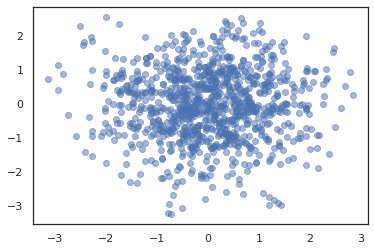
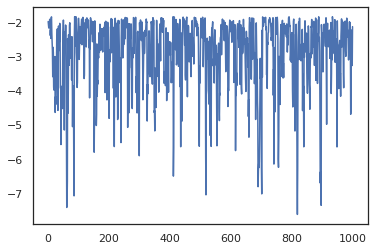
برای اجرای زنجیره ای متعدد، ما هم می تواند دسته ای از کشورهای تصویب به sample_chain یا استفاده vmap (هر چند ما هنوز بررسی تفاوت عملکرد این دو نگرش).

states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros([10, 2]))
plt.figure()
for i in range(10):
  plt.scatter(*states[:, i].T, alpha=0.5)
plt.figure()
for i in range(10):
  plt.plot(log_probs[:, i], alpha=0.5)
plt.show()

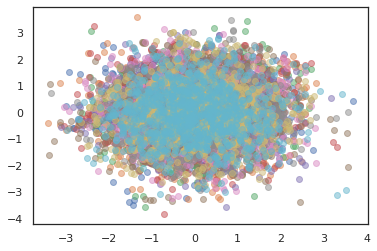
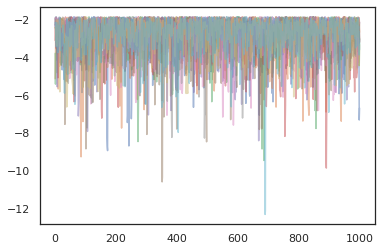
بهینه سازها

TFP در JAX از برخی بهینه سازهای مهم مانند BFGS و L-BFGS پشتیبانی می کند. بیایید یک تابع تلفات درجه دوم مقیاس بندی شده ساده تنظیم کنیم.

minimum = jnp.array([1.0, 1.0])  # The center of the quadratic bowl.
scales = jnp.array([2.0, 3.0])  # The scales along the two axes.

# The objective function and the gradient.
def quadratic_loss(x):
  return jnp.sum(scales * jnp.square(x - minimum))

start = jnp.array([0.6, 0.8])  # Starting point for the search.

BFGS می تواند حداقل این ضرر را پیدا کند.

optim_results = tfp.optimizer.bfgs_minimize(
    value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)

# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)

Function evaluations: 5

L-BFGS هم همینطور.

optim_results = tfp.optimizer.lbfgs_minimize(
    value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)

# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)

Function evaluations: 5

برای vmap L-BFGS، اجازه دهید مجموعه ای تا یک تابع است که بهینه سازی از دست دادن برای یک نقطه شروع است.

def optimize_single(start):
  return tfp.optimizer.lbfgs_minimize(
      value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)

all_results = jit(vmap(optimize_single))(
    random.normal(random.PRNGKey(0), (10, 2)))
assert all(all_results.converged)
for i in range(10):
  np.testing.assert_allclose(optim_results.position[i], minimum)
print("Function evaluations: %s" % all_results.num_objective_evaluations)

Function evaluations: [6 6 9 6 6 8 6 8 5 9]

هشدارها

تفاوت‌های اساسی بین TF و JAX وجود دارد، برخی از رفتارهای TFP بین دو زیرلایه متفاوت است و همه عملکردها پشتیبانی نمی‌شوند. مثلا،

• بهره وری کل عوامل در JAX هیچ چیزی مانند پشتیبانی نمی tf.Variable از چیزی شبیه به آن در JAX وجود دارد. این همچنین بدان معنی آب و برق مانند tfp.util.TransformedVariable ها یا پشتیبانی نمی شود.
• tfp.layers است در باطن پشتیبانی نشده است، با توجه به وابستگی آن به Keras و tf.Variable است.
• tfp.math.minimize کار در بهره وری کل عوامل در JAX نه به خاطر وابستگی آن به tf.Variable .
• با TFP در JAX، اشکال تانسور همیشه مقادیر صحیح مشخص هستند و مانند TFP در TF هرگز ناشناخته/پویا نیستند.
• تصادفی بودن کاذب در TF و JAX متفاوت است (به پیوست مراجعه کنید).
• کتابخانه ها در tfp.experimental تضمین شده نیست در بستر JAX وجود دارد.
• قوانین تبلیغ Dtype بین TF و JAX متفاوت است. TFP در JAX سعی می کند به معنای dtype TF در داخل احترام بگذارد، تا سازگاری داشته باشد.
• Bijectors هنوز به عنوان JAX pytrees ثبت نشده اند.

برای دیدن لیست کامل از آنچه در بهره وری کل عوامل در JAX پشتیبانی، لطفا به مراجعه مستندات API .

نتیجه

ما بسیاری از ویژگی‌های TFP را به JAX منتقل کرده‌ایم و از دیدن آنچه که همه خواهند ساخت هیجان‌زده هستیم. برخی از عملکردها هنوز پشتیبانی نمی شوند. اگر ما چیزی برای شما مهم از دست رفته (و یا اگر شما پیدا کردن یک اشکال!) لطفا به ما - شما می توانید ایمیل tfprobability@tensorflow.org یا فایل یک موضوع در مخزن گیتهاب ما .

ضمیمه: تصادفی کاذب در JAX

مدل نسل عدد شبه تصادفی JAX است (PRNG) بی وطن است. بر خلاف یک مدل حالت دار، هیچ حالت جهانی قابل تغییری وجود ندارد که پس از هر قرعه کشی تصادفی تغییر کند. در مدل JAX، ما با یک کلید PRNG، که مانند یک جفت از اعداد صحیح 32 بیتی عمل می کند شروع می شود. ما می توانیم این کلید با استفاده از ساخت jax.random.PRNGKey .

key = random.PRNGKey(0)  # Creates a key with value [0, 0]
print(key)

[0 0]

توابع تصادفی در JAX یک کلید مصرف کنیدتا تولید یک متغیره تصادفی، به این معنی که آنها باید دوباره استفاده نمی شود. برای مثال، ما می توانید استفاده کنید key برای نمونه یک ارزش به طور معمول توزیع، اما ما باید استفاده نمی key دوباره در جای دیگر. علاوه بر این، عبور همان مقدار به random.normal خواهد شد که ارزش یکسانی است.

print(random.normal(key))

-0.20584226

بنابراین چگونه از یک کلید چندین نمونه ترسیم کنیم؟ پاسخ تقسیم کلیدی است. ایده اصلی این است که ما می توانیم تقسیم PRNGKey را به چند و هر یک از کلید های جدید می تواند به عنوان یک منبع مستقل از اتفاقی درمان می شود.

key1, key2 = random.split(key, num=2)
print(key1, key2)

[4146024105  967050713] [2718843009 1272950319]

تقسیم کلید قطعی است اما آشفته است، بنابراین هر کلید جدید اکنون می تواند برای ترسیم یک نمونه تصادفی مجزا استفاده شود.

print(random.normal(key1), random.normal(key2))

0.14389051 -1.2515389

برای جزئیات بیشتر در مورد مدل تقسیم کلیدی قطعی JAX، نگاه کنید به این راهنما .