 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar cuaderno Descargar cuaderno |
TensorFlow Probabilidad (PTF) es una biblioteca para el razonamiento probabilístico y análisis estadístico que ahora también funciona en JAX ! Para aquellos que no estén familiarizados, JAX es una biblioteca para computación numérica acelerada basada en transformaciones de funciones componibles.
TFP en JAX admite muchas de las funciones más útiles de TFP normal al tiempo que conserva las abstracciones y las API con las que muchos usuarios de TFP ahora se sienten cómodos.
Configuración
PTF en JAX no depende de TensorFlow; desinstalemos TensorFlow de este Colab por completo.
pip uninstall tensorflow -y -q
Podemos instalar TFP en JAX con las últimas versiones nocturnas de TFP.
pip install -Uq tfp-nightly[jax] > /dev/null
Vamos a importar algunas bibliotecas útiles de Python.
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn import datasets
sns.set(style='white')
/usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead. import pandas.util.testing as tm
También importemos algunas funciones JAX básicas.
import jax.numpy as jnp
from jax import grad
from jax import jit
from jax import random
from jax import value_and_grad
from jax import vmap
Importación de TFP en JAX
Para utilizar la PTF en JAX, simplemente importar el jax "sustrato" y utilizarlo como lo haría normalmente tfp :
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
tfpk = tfp.math.psd_kernels
Demostración: regresión logística bayesiana
Para demostrar lo que podemos hacer con el backend JAX, implementaremos la regresión logística bayesiana aplicada al conjunto de datos Iris clásico.
Primero, importemos el conjunto de datos de Iris y extraigamos algunos metadatos.
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
Podemos definir el modelo utilizando tfd.JointDistributionCoroutine . Pondremos priores normales estándar en ambos los pesos y el término sesgo a continuación, escribir target_log_prob función que los pasadores de etiquetas muestra a los datos.
Root = tfd.JointDistributionCoroutine.Root
def model():
w = yield Root(tfd.Sample(tfd.Normal(0., 1.),
sample_shape=(num_features, num_classes)))
b = yield Root(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(num_classes,)))
logits = jnp.dot(features, w) + b
yield tfd.Independent(tfd.Categorical(logits=logits),
reinterpreted_batch_ndims=1)
dist = tfd.JointDistributionCoroutine(model)
def target_log_prob(*params):
return dist.log_prob(params + (labels,))
Nos muestra a partir de dist para producir un estado inicial de MCMC. Luego podemos definir una función que toma una clave aleatoria y un estado inicial, y produce 500 muestras de un muestreador sin giro en U (NUTS). Tenga en cuenta que podemos utilizar transformaciones JAX como jit para compilar nuestra muestreador tuercas con XLA.
init_key, sample_key = random.split(random.PRNGKey(0))
init_params = tuple(dist.sample(seed=init_key)[:-1])
@jit
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-3)
return tfp.mcmc.sample_chain(500,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
num_burnin_steps=500,
seed=key)
states, log_probs = run_chain(sample_key, init_params)
plt.figure()
plt.plot(log_probs)
plt.ylabel('Target Log Prob')
plt.xlabel('Iterations of NUTS')
plt.show()
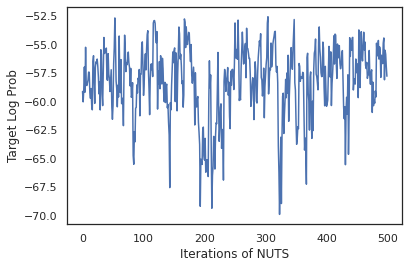
Usemos nuestras muestras para realizar el promedio del modelo bayesiano (BMA) promediando las probabilidades predichas de cada conjunto de pesos.
Primero, escribamos una función que para un conjunto dado de parámetros producirá las probabilidades de cada clase. Podemos utilizar dist.sample_distributions para obtener la distribución final en el modelo.
def classifier_probs(params):
dists, _ = dist.sample_distributions(seed=random.PRNGKey(0),
value=params + (None,))
return dists[-1].distribution.probs_parameter()
Podemos vmap(classifier_probs) sobre el conjunto de muestras para obtener las probabilidades predichas de clase para cada una de nuestras muestras. Luego calculamos la precisión promedio en cada muestra y la precisión del promedio del modelo bayesiano.
all_probs = jit(vmap(classifier_probs))(states)
print('Average accuracy:', jnp.mean(all_probs.argmax(axis=-1) == labels))
print('BMA accuracy:', jnp.mean(all_probs.mean(axis=0).argmax(axis=-1) == labels))
Average accuracy: 0.96952 BMA accuracy: 0.97999996
¡Parece que BMA reduce nuestra tasa de error en casi un tercio!
Fundamentos
PTF en JAX tiene una API idéntica a TF, donde en lugar de aceptar objetos TF como tf.Tensor es que acepta el análogo de JAX. Por ejemplo, siempre que sea un tf.Tensor fue utilizado anteriormente como entrada, la API ahora espera un JAX DeviceArray . En lugar de devolver un tf.Tensor , los métodos de la PTF volverán DeviceArray s. PTF en JAX también trabaja con estructuras jerarquizadas de objetos JAX, como una lista o diccionario de DeviceArray s.
Distribuciones
La mayoría de las distribuciones de TFP son compatibles con JAX con una semántica muy similar a sus contrapartes de TF. También se registran como JAX Pytrees , para que puedan ser entradas y salidas de las funciones transformadas con JAX.
Distribuciones básicas
El log_prob método para distribuciones funciona de la misma.
dist = tfd.Normal(0., 1.)
print(dist.log_prob(0.))
-0.9189385
Muestreo de una distribución requiere pasar de forma explícita en un PRNGKey (o una lista de números enteros) como la seed argumento de palabra clave. No pasar explícitamente una semilla arrojará un error.
tfd.Normal(0., 1.).sample(seed=random.PRNGKey(0))
DeviceArray(-0.20584226, dtype=float32)
La semántica de forma para distribuciones siguen siendo los mismos en JAX, donde las distribuciones tendrán cada uno un event_shape y una batch_shape y dibujo muchas muestras agregará adicionales sample_shape dimensiones.
Por ejemplo, un tfd.MultivariateNormalDiag con parámetros vector tendrá una forma evento vector y la forma de lote vacío.
dist = tfd.MultivariateNormalDiag(
loc=jnp.zeros(5),
scale_diag=jnp.ones(5)
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: (5,) Batch shape: ()
Por otro lado, un tfd.Normal parametrizado con vectores tendrá una forma evento y lote vector forma escalar.
dist = tfd.Normal(
loc=jnp.ones(5),
scale=jnp.ones(5),
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: () Batch shape: (5,)
La semántica de tomar log_prob de muestras funciona de la misma en JAX también.
dist = tfd.Normal(jnp.zeros(5), jnp.ones(5))
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
dist = tfd.Independent(tfd.Normal(jnp.zeros(5), jnp.ones(5)), 1)
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
(10, 2, 5) (10, 2)
Debido a JAX DeviceArray s son compatibles con las bibliotecas como NumPy y Matplotlib, podemos alimentar las muestras directamente en un dibujo de las funciones.
sns.distplot(tfd.Normal(0., 1.).sample(1000, seed=random.PRNGKey(0)))
plt.show()
Distribution métodos son compatibles con las transformaciones JAX.
sns.distplot(jit(vmap(lambda key: tfd.Normal(0., 1.).sample(seed=key)))(
random.split(random.PRNGKey(0), 2000)))
plt.show()
x = jnp.linspace(-5., 5., 100)
plt.plot(x, jit(vmap(grad(tfd.Normal(0., 1.).prob)))(x))
plt.show()
Debido a que las distribuciones de la PTF se registran como nodos pytree JAX, podemos escribir funciones con distribuciones como entradas o salidas y transformarlos usando jit , pero aún no se admiten como argumentos para vmap funciones -ed.
@jit
def random_distribution(key):
loc_key, scale_key = random.split(key)
loc, log_scale = random.normal(loc_key), random.normal(scale_key)
return tfd.Normal(loc, jnp.exp(log_scale))
random_dist = random_distribution(random.PRNGKey(0))
print(random_dist.mean(), random_dist.variance())
0.14389051 0.081832744
Distribuciones transformadas
Distribuciones transformadas, es decir, las distribuciones cuyas muestras se pasan a través de un Bijector también trabajan fuera de la caja (bijectors trabajan también! Véase más adelante).
dist = tfd.TransformedDistribution(
tfd.Normal(0., 1.),
tfb.Sigmoid()
)
sns.distplot(dist.sample(1000, seed=random.PRNGKey(0)))
plt.show()
Distribuciones conjuntas
PTF ofrece JointDistribution s para permitir la combinación de distribuciones de componentes en una sola distribución a través de múltiples variables aleatorias. Actualmente, la PTF ofrece tres variantes básicas ( JointDistributionSequential , JointDistributionNamed y JointDistributionCoroutine ) todos los cuales son compatibles con JAX. Los AutoBatched variantes también son compatibles.
dist = tfd.JointDistributionSequential([
tfd.Normal(0., 1.),
lambda x: tfd.Normal(x, 1e-1)
])
plt.scatter(*dist.sample(1000, seed=random.PRNGKey(0)), alpha=0.5)
plt.show()
joint = tfd.JointDistributionNamed(dict(
e= tfd.Exponential(rate=1.),
n= tfd.Normal(loc=0., scale=2.),
m=lambda n, e: tfd.Normal(loc=n, scale=e),
x=lambda m: tfd.Sample(tfd.Bernoulli(logits=m), 12),
))
joint.sample(seed=random.PRNGKey(0))
{'e': DeviceArray(3.376818, dtype=float32),
'm': DeviceArray(2.5449684, dtype=float32),
'n': DeviceArray(-0.6027825, dtype=float32),
'x': DeviceArray([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int32)}
Root = tfd.JointDistributionCoroutine.Root
def model():
e = yield Root(tfd.Exponential(rate=1.))
n = yield Root(tfd.Normal(loc=0, scale=2.))
m = yield tfd.Normal(loc=n, scale=e)
x = yield tfd.Sample(tfd.Bernoulli(logits=m), 12)
joint = tfd.JointDistributionCoroutine(model)
joint.sample(seed=random.PRNGKey(0))
StructTuple(var0=DeviceArray(0.17315261, dtype=float32), var1=DeviceArray(-3.290489, dtype=float32), var2=DeviceArray(-3.1949058, dtype=float32), var3=DeviceArray([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], dtype=int32))
Otras distribuciones
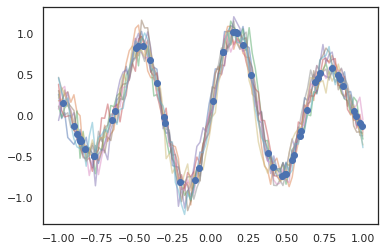
¡Los procesos gaussianos también funcionan en modo JAX!
k1, k2, k3 = random.split(random.PRNGKey(0), 3)
observation_noise_variance = 0.01
f = lambda x: jnp.sin(10*x[..., 0]) * jnp.exp(-x[..., 0]**2)
observation_index_points = random.uniform(
k1, [50], minval=-1.,maxval= 1.)[..., jnp.newaxis]
observations = f(observation_index_points) + tfd.Normal(
loc=0., scale=jnp.sqrt(observation_noise_variance)).sample(seed=k2)
index_points = jnp.linspace(-1., 1., 100)[..., jnp.newaxis]
kernel = tfpk.ExponentiatedQuadratic(length_scale=0.1)
gprm = tfd.GaussianProcessRegressionModel(
kernel=kernel,
index_points=index_points,
observation_index_points=observation_index_points,
observations=observations,
observation_noise_variance=observation_noise_variance)
samples = gprm.sample(10, seed=k3)
for i in range(10):
plt.plot(index_points, samples[i], alpha=0.5)
plt.plot(observation_index_points, observations, marker='o', linestyle='')
plt.show()
Los modelos ocultos de Markov también son compatibles.
initial_distribution = tfd.Categorical(probs=[0.8, 0.2])
transition_distribution = tfd.Categorical(probs=[[0.7, 0.3],
[0.2, 0.8]])
observation_distribution = tfd.Normal(loc=[0., 15.], scale=[5., 10.])
model = tfd.HiddenMarkovModel(
initial_distribution=initial_distribution,
transition_distribution=transition_distribution,
observation_distribution=observation_distribution,
num_steps=7)
print(model.mean())
print(model.log_prob(jnp.zeros(7)))
print(model.sample(seed=random.PRNGKey(0)))
[3. 6. 7.5 8.249999 8.625001 8.812501 8.90625 ] /usr/local/lib/python3.6/dist-packages/tensorflow_probability/substrates/jax/distributions/hidden_markov_model.py:483: UserWarning: HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug in which the transition model was applied prior to the initial step. This bug has been fixed. You may observe a slight change in behavior. 'HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug ' -19.855635 [ 1.3641367 0.505798 1.3626463 3.6541772 2.272286 15.10309 22.794212 ]
Unas distribuciones como PixelCNN no son compatibles todavía debido a las dependencias estrictas sobre TensorFlow o XLA incompatibilidades.
Biyectores
¡La mayoría de los biyectores de TFP son compatibles con JAX en la actualidad!
tfb.Exp().inverse(1.)
DeviceArray(0., dtype=float32)
bij = tfb.Shift(1.)(tfb.Scale(3.))
print(bij.forward(jnp.ones(5)))
print(bij.inverse(jnp.ones(5)))
[4. 4. 4. 4. 4.] [0. 0. 0. 0. 0.]
b = tfb.FillScaleTriL(diag_bijector=tfb.Exp(), diag_shift=None)
print(b.forward(x=[0., 0., 0.]))
print(b.inverse(y=[[1., 0], [.5, 2]]))
[[1. 0.] [0. 1.]] [0.6931472 0.5 0. ]
b = tfb.Chain([tfb.Exp(), tfb.Softplus()])
# or:
# b = tfb.Exp()(tfb.Softplus())
print(b.forward(-jnp.ones(5)))
[1.3678794 1.3678794 1.3678794 1.3678794 1.3678794]
Bijectors son compatibles con las transformaciones JAX como jit , grad y vmap .
jit(vmap(tfb.Exp().inverse))(jnp.arange(4.))
DeviceArray([ -inf, 0. , 0.6931472, 1.0986123], dtype=float32)
x = jnp.linspace(0., 1., 100)
plt.plot(x, jit(grad(lambda x: vmap(tfb.Sigmoid().inverse)(x).sum()))(x))
plt.show()
Algunos bijectors, como RealNVP y FFJORD aún no son compatibles.
MCMC
Hemos portado tfp.mcmc a JAX así, por lo que podemos ejecutar algoritmos como hamiltoniano Monte Carlo (HMC) y el n-U-Turn-Sampler (NUTS) en JAX.
target_log_prob = tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)).log_prob
A diferencia de la PTF en la TF, estamos obligados a pasar una PRNGKey en sample_chain usando la seed argumento de palabra clave.
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-1)
return tfp.mcmc.sample_chain(1000,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
seed=key)
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros(2))
plt.figure()
plt.scatter(*states.T, alpha=0.5)
plt.figure()
plt.plot(log_probs)
plt.show()
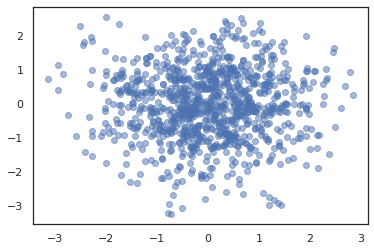
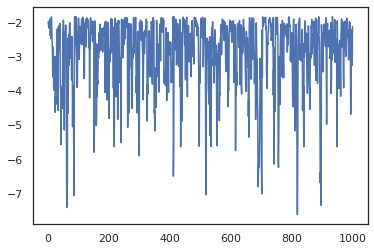
Para ejecutar múltiples cadenas, podemos pasar ya sea un lote de estados en sample_chain o uso vmap (aunque todavía no hemos explorado las diferencias de rendimiento entre los dos enfoques).
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros([10, 2]))
plt.figure()
for i in range(10):
plt.scatter(*states[:, i].T, alpha=0.5)
plt.figure()
for i in range(10):
plt.plot(log_probs[:, i], alpha=0.5)
plt.show()
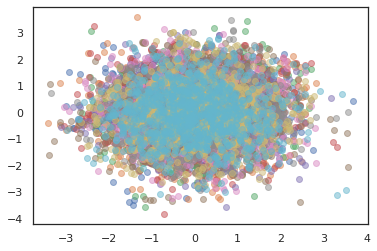
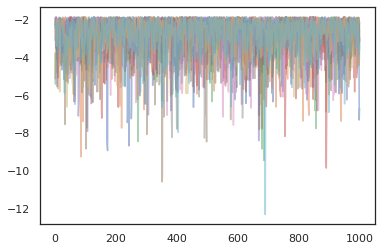
Optimizadores
TFP en JAX admite algunos optimizadores importantes como BFGS y L-BFGS. Configuremos una función de pérdida cuadrática escalada simple.
minimum = jnp.array([1.0, 1.0]) # The center of the quadratic bowl.
scales = jnp.array([2.0, 3.0]) # The scales along the two axes.
# The objective function and the gradient.
def quadratic_loss(x):
return jnp.sum(scales * jnp.square(x - minimum))
start = jnp.array([0.6, 0.8]) # Starting point for the search.
BFGS puede encontrar el mínimo de esta pérdida.
optim_results = tfp.optimizer.bfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
También puede L-BFGS.
optim_results = tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
Para vmap L-BFGS, vamos a configurar una función que optimiza la pérdida de un único punto de partida.
def optimize_single(start):
return tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
all_results = jit(vmap(optimize_single))(
random.normal(random.PRNGKey(0), (10, 2)))
assert all(all_results.converged)
for i in range(10):
np.testing.assert_allclose(optim_results.position[i], minimum)
print("Function evaluations: %s" % all_results.num_objective_evaluations)
Function evaluations: [6 6 9 6 6 8 6 8 5 9]
Advertencias
Existen algunas diferencias fundamentales entre TF y JAX, algunos comportamientos de TFP serán diferentes entre los dos sustratos y no todas las funciones son compatibles. Por ejemplo,
- PTF en JAX no soporta nada por el estilo
tf.Variableya nada parecido existe en JAX. Esto también significa utilidades comotfp.util.TransformedVariableno son compatibles tampoco. -
tfp.layersno se admite en el back-end, sin embargo, debido a su dependencia de Keras ytf.Variables. -
tfp.math.minimizeno funciona en la PTF en JAX debido a su dependencia detf.Variable. - Con TFP en JAX, las formas de tensor son siempre valores enteros concretos y nunca son desconocidas / dinámicas como en TFP en TF.
- La pseudoaleatoriedad se maneja de manera diferente en TF y JAX (ver apéndice).
- Bibliotecas en
tfp.experimentalno se garantiza que existen en el sustrato JAX. - Las reglas de promoción de tipo D son diferentes entre TF y JAX. TFP en JAX intenta respetar la semántica dtype de TF internamente, para mantener la coherencia.
- Los biyectores aún no se han registrado como pytrees JAX.
Para ver la lista completa de lo que se admite en la PTF en JAX, consulte la documentación de la API .
Conclusión
Hemos portado muchas de las funciones de TFP a JAX y estamos emocionados de ver lo que todos construirán. Algunas funciones aún no son compatibles; si nos hemos perdido algo importante que usted (o si encuentra un error!) por favor, llegar a nosotros - se puede enviar por correo electrónico tfprobability@tensorflow.org o presentar un problema en nuestro repositorio de Github .
Apéndice: pseudoaleatoriedad en JAX
Modelo de generación de números pseudoaleatorios (PRNG) de Jax no tiene estado. A diferencia de un modelo con estado, no existe un estado global mutable que evolucione después de cada sorteo aleatorio. En el modelo de JAX, comenzamos con una clave PRNG, que actúa como un par de enteros de 32 bits. Podemos construir estas teclas utilizando jax.random.PRNGKey .
key = random.PRNGKey(0) # Creates a key with value [0, 0]
print(key)
[0 0]
Funciones aleatorias en JAX consumen una clave para producir de forma determinista una variable aleatoria, lo que significa que no deben ser utilizados de nuevo. Por ejemplo, podemos utilizar key para muestrear un valor distribuido normalmente, pero no debemos usar key de nuevo en otro lugar. Además, pasando el mismo valor en random.normal producirá el mismo valor.
print(random.normal(key))
-0.20584226
Entonces, ¿cómo podemos extraer varias muestras de una sola clave? La respuesta es la división de claves. La idea básica es que podemos dividir un PRNGKey en múltiples y cada una de las nuevas claves puede ser tratada como una fuente independiente de aleatoriedad.
key1, key2 = random.split(key, num=2)
print(key1, key2)
[4146024105 967050713] [2718843009 1272950319]
La división de claves es determinista pero caótica, por lo que ahora se puede utilizar cada nueva clave para extraer una muestra aleatoria distinta.
print(random.normal(key1), random.normal(key2))
0.14389051 -1.2515389
Para más detalles sobre el modelo determinista clave de la división de Jax, consulte esta guía .
