 TensorFlow.org এ দেখুন TensorFlow.org এ দেখুন |  Google Colab-এ চালান Google Colab-এ চালান |  GitHub-এ উৎস দেখুন GitHub-এ উৎস দেখুন |  নোটবুক ডাউনলোড করুন নোটবুক ডাউনলোড করুন |
TensorFlow সম্ভাব্যতা (TFP) সম্ভাব্য যুক্তি এবং পরিসংখ্যান বিশ্লেষণ করে এখন কাজ করে একটি লাইব্রেরি Jax ! যারা পরিচিত নন তাদের জন্য, JAX হল কম্পোজেবল ফাংশন ট্রান্সফরমেশনের উপর ভিত্তি করে ত্বরিত সংখ্যাসূচক কম্পিউটিংয়ের জন্য একটি লাইব্রেরি।
JAX-এ TFP নিয়মিত TFP-এর অনেক বেশি দরকারী কার্যকারিতা সমর্থন করে যখন অনেক TFP ব্যবহারকারী এখন আরামদায়ক বিমূর্ততা এবং API সংরক্ষণ করে।
সেটআপ
TFP Jax উপর TensorFlow উপর নির্ভর করে না; এই Colab থেকে TensorFlow সম্পূর্ণরূপে আনইনস্টল করা যাক।
pip uninstall tensorflow -y -q
আমরা JAX-এ TFP-এর সর্বশেষ রাতের বিল্ডগুলির সাথে TFP ইনস্টল করতে পারি।
pip install -Uq tfp-nightly[jax] > /dev/null
আসুন কিছু দরকারী পাইথন লাইব্রেরি আমদানি করি।
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn import datasets
sns.set(style='white')
/usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead. import pandas.util.testing as tm
এর কিছু মৌলিক JAX কার্যকারিতাও আমদানি করা যাক।
import jax.numpy as jnp
from jax import grad
from jax import jit
from jax import random
from jax import value_and_grad
from jax import vmap
JAX-এ TFP আমদানি করা হচ্ছে
Jax উপর TFP ব্যবহার করার জন্য, কেবল আমদানি jax "স্তর" এবং এটি ব্যবহার হিসাবে আপনি সাধারণত হবে tfp :
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
tfpk = tfp.math.psd_kernels
ডেমো: বায়েসিয়ান লজিস্টিক রিগ্রেশন
JAX ব্যাকএন্ডের সাথে আমরা কী করতে পারি তা প্রদর্শন করতে, আমরা ক্লাসিক আইরিস ডেটাসেটে প্রয়োগ করা Bayesian লজিস্টিক রিগ্রেশন বাস্তবায়ন করব।
প্রথমে, আইরিস ডেটাসেট ইম্পোর্ট করি এবং কিছু মেটাডেটা বের করি।
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
আমরা ব্যবহার মডেল বর্ণনা করতে পারেন tfd.JointDistributionCoroutine । আমরা উভয় ওজন ও পক্ষপাত পদের উপর আদর্শ স্বাভাবিক গতকাল দেশের সর্বোচ্চ তাপমাত্রা রেখে দেব তারপর একটি লিখতে target_log_prob ফাংশন যা পিনের তথ্য নমুনা লেবেলগুলি।
Root = tfd.JointDistributionCoroutine.Root
def model():
w = yield Root(tfd.Sample(tfd.Normal(0., 1.),
sample_shape=(num_features, num_classes)))
b = yield Root(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(num_classes,)))
logits = jnp.dot(features, w) + b
yield tfd.Independent(tfd.Categorical(logits=logits),
reinterpreted_batch_ndims=1)
dist = tfd.JointDistributionCoroutine(model)
def target_log_prob(*params):
return dist.log_prob(params + (labels,))
আমরা থেকে নমুনা dist এমসিএমসি জন্য একটি প্রাথমিক অবস্থায় উত্পাদন করতে। তারপরে আমরা একটি ফাংশন সংজ্ঞায়িত করতে পারি যা একটি র্যান্ডম কী এবং একটি প্রাথমিক অবস্থায় নেয় এবং একটি No-U-Turn-Sampler (NUTS) থেকে 500টি নমুনা তৈরি করে। মনে রাখবেন আমরা মত Jax রূপান্তরের ব্যবহার করতে পারেন jit XLA ব্যবহার করে আমাদের পাগল টাঙানো নকশা-বোনা কম্পাইল করার।
init_key, sample_key = random.split(random.PRNGKey(0))
init_params = tuple(dist.sample(seed=init_key)[:-1])
@jit
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-3)
return tfp.mcmc.sample_chain(500,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
num_burnin_steps=500,
seed=key)
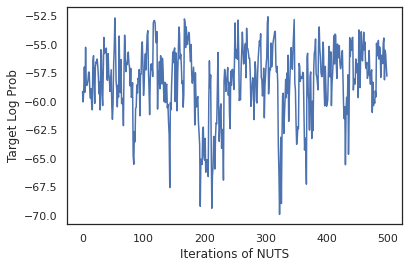
states, log_probs = run_chain(sample_key, init_params)
plt.figure()
plt.plot(log_probs)
plt.ylabel('Target Log Prob')
plt.xlabel('Iterations of NUTS')
plt.show()
আসুন ওজনের প্রতিটি সেটের পূর্বাভাসিত সম্ভাবনার গড় করে বেয়েসিয়ান মডেল গড় (BMA) সম্পাদন করতে আমাদের নমুনাগুলি ব্যবহার করি।
প্রথমে একটি ফাংশন লিখি যা প্রদত্ত প্যারামিটারের সেটের জন্য প্রতিটি ক্লাসে সম্ভাব্যতা তৈরি করবে। আমরা ব্যবহার করতে পারি dist.sample_distributions মডেল চূড়ান্ত বন্টন প্রাপ্ত।
def classifier_probs(params):
dists, _ = dist.sample_distributions(seed=random.PRNGKey(0),
value=params + (None,))
return dists[-1].distribution.probs_parameter()
আমরা পারি vmap(classifier_probs) নমুনার সেট উপর আমাদের নমুনা প্রত্যেকের জন্য পূর্বাভাস বর্গ সম্ভাব্যতা জন্য। তারপরে আমরা প্রতিটি নমুনা জুড়ে গড় নির্ভুলতা এবং বায়েসিয়ান মডেল গড় থেকে নির্ভুলতা গণনা করি।
all_probs = jit(vmap(classifier_probs))(states)
print('Average accuracy:', jnp.mean(all_probs.argmax(axis=-1) == labels))
print('BMA accuracy:', jnp.mean(all_probs.mean(axis=0).argmax(axis=-1) == labels))
Average accuracy: 0.96952 BMA accuracy: 0.97999996
মনে হচ্ছে বিএমএ আমাদের ত্রুটির হার প্রায় এক তৃতীয়াংশ কমিয়েছে!
মৌলিক
TFP Jax উপর মেমরি একটি অভিন্ন এপিআই যেখানে মেমরি বস্তু গ্রহণ পরিবর্তে মত tf.Tensor গুলি এটা Jax অ্যানালগ গ্রহণ করে। উদাহরণস্বরূপ, যেখানেই থাকুন না কেন একটি tf.Tensor পূর্বে ইনপুট হিসাবে ব্যবহার করা হয়েছিল, এপিআই এখন A Jax আশা DeviceArray । পরিবর্তে একটি ফিরে tf.Tensor , TFP পদ্ধতি ফিরে আসবে DeviceArray গুলি। TFP Jax এছাড়াও Jax বস্তুর নেস্টেড কাঠামো, একটি তালিকা বা অভিধান মত সাথে কাজ করে DeviceArray গুলি।
বিতরণ
TFP-এর বেশিরভাগ ডিস্ট্রিবিউশন JAX-এ সমর্থিত হয় তাদের TF কাউন্টারপার্টের সাথে খুব মিল শব্দার্থক। তারা যেমন নিবন্ধিত Jax Pytrees , তাই তারা ইনপুট এবং Jax-রুপান্তরিত ফাংশন আউটপুট হতে পারে।
মৌলিক বিতরণ
log_prob ডিস্ট্রিবিউশন জন্য পদ্ধতি একই কাজ করে।
dist = tfd.Normal(0., 1.)
print(dist.log_prob(0.))
-0.9189385
একটি বিতরণ থেকে স্যাম্পলিং স্পষ্টভাবে একটি ক্ষণস্থায়ী প্রয়োজন PRNGKey হিসাবে (পূর্ণসংখ্যার তালিকা বা) seed শব্দ যুক্তি। একটি বীজ স্পষ্টভাবে পাস করতে ব্যর্থ একটি ত্রুটি নিক্ষেপ করা হবে.
tfd.Normal(0., 1.).sample(seed=random.PRNGKey(0))
DeviceArray(-0.20584226, dtype=float32)
ডিস্ট্রিবিউশন আকৃতি শব্দার্থবিদ্যা Jax, যেখানে ডিস্ট্রিবিউশন প্রতিটি একটি থাকবে একই থাকবে event_shape এবং batch_shape এবং অনেক নমুনার অঙ্কন অতিরিক্ত যোগ হবে sample_shape মাত্রা।
উদাহরণস্বরূপ, একটি tfd.MultivariateNormalDiag ভেক্টর পরামিতি সঙ্গে একটি ভেক্টর ঘটনা আকৃতি এবং খালি ব্যাচ আকৃতি হবে।
dist = tfd.MultivariateNormalDiag(
loc=jnp.zeros(5),
scale_diag=jnp.ones(5)
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: (5,) Batch shape: ()
অন্যদিকে, একটি tfd.Normal ভেক্টর দিয়ে স্থিতিমাপ স্কেলের ঘটনা আকৃতি এবং ভেক্টর ব্যাচ আকৃতি হবে।
dist = tfd.Normal(
loc=jnp.ones(5),
scale=jnp.ones(5),
)
print('Event shape:', dist.event_shape)
print('Batch shape:', dist.batch_shape)
Event shape: () Batch shape: (5,)
গ্রহণের শব্দার্থবিদ্যা log_prob নমুনার খুব Jax একই কাজ করে।
dist = tfd.Normal(jnp.zeros(5), jnp.ones(5))
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
dist = tfd.Independent(tfd.Normal(jnp.zeros(5), jnp.ones(5)), 1)
s = dist.sample(sample_shape=(10, 2), seed=random.PRNGKey(0))
print(dist.log_prob(s).shape)
(10, 2, 5) (10, 2)
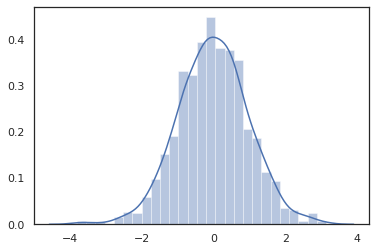
কারণ Jax DeviceArray গুলি NumPy এবং Matplotlib মত লাইব্রেরি সঙ্গে সামঞ্জস্যপূর্ণ, আমরা একটি ষড়যন্ত্র ফাংশন মধ্যে সরাসরি নমুনা খাওয়ানোর পারবেন না।
sns.distplot(tfd.Normal(0., 1.).sample(1000, seed=random.PRNGKey(0)))
plt.show()
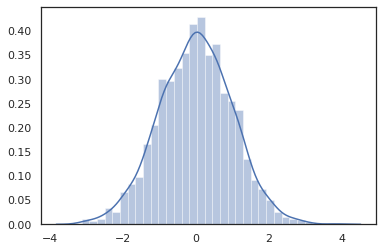
Distribution পদ্ধতি Jax রূপান্তরের সঙ্গে সামঞ্জস্যপূর্ণ।
sns.distplot(jit(vmap(lambda key: tfd.Normal(0., 1.).sample(seed=key)))(
random.split(random.PRNGKey(0), 2000)))
plt.show()
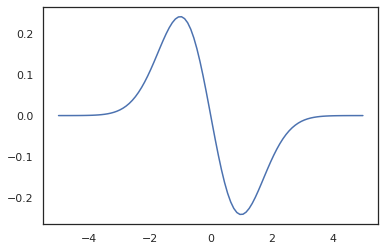
x = jnp.linspace(-5., 5., 100)
plt.plot(x, jit(vmap(grad(tfd.Normal(0., 1.).prob)))(x))
plt.show()
TFP ডিস্ট্রিবিউশন Jax pytree নোড হিসাবে নিবন্ধিত করতে থাকার কারণে, আমরা ইনপুট বা আউটপুট হিসাবে ডিস্ট্রিবিউশন সঙ্গে ফাংশন লিখতে পারেন এবং ব্যবহার করে সেগুলি রুপান্তর jit , কিন্তু তারা এখনো আর্গুমেন্ট হিসেবে সমর্থিত নয় vmap -ed ফাংশন।
@jit
def random_distribution(key):
loc_key, scale_key = random.split(key)
loc, log_scale = random.normal(loc_key), random.normal(scale_key)
return tfd.Normal(loc, jnp.exp(log_scale))
random_dist = random_distribution(random.PRNGKey(0))
print(random_dist.mean(), random_dist.variance())
0.14389051 0.081832744
রূপান্তরিত বিতরণ
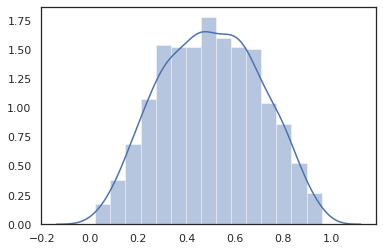
রুপান্তরিত ডিস্ট্রিবিউশন অর্থাৎ ডিস্ট্রিবিউশন যার নমুনা একটি মাধ্যমে গৃহীত হয় Bijector এছাড়াও বাক্সের বাইরে কাজ (bijectors খুব কাজ! নীচে দেখুন)।
dist = tfd.TransformedDistribution(
tfd.Normal(0., 1.),
tfb.Sigmoid()
)
sns.distplot(dist.sample(1000, seed=random.PRNGKey(0)))
plt.show()
যৌথ বিতরণ
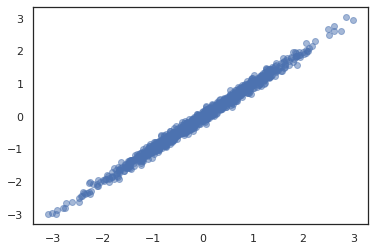
TFP উপলব্ধ করা হয় JointDistribution s একাধিক র্যান্ডম ভেরিয়েবল উপর একটি একক বন্টন মধ্যে উপাদান ডিস্ট্রিবিউশন মিশ্রন সক্রিয়। বর্তমানে, TFP অফার তিন কোর রূপগুলো ( JointDistributionSequential , JointDistributionNamed এবং JointDistributionCoroutine ) যা সব Jax মধ্যে সমর্থিত। AutoBatched রূপগুলো সব সমর্থিত।
dist = tfd.JointDistributionSequential([
tfd.Normal(0., 1.),
lambda x: tfd.Normal(x, 1e-1)
])
plt.scatter(*dist.sample(1000, seed=random.PRNGKey(0)), alpha=0.5)
plt.show()
joint = tfd.JointDistributionNamed(dict(
e= tfd.Exponential(rate=1.),
n= tfd.Normal(loc=0., scale=2.),
m=lambda n, e: tfd.Normal(loc=n, scale=e),
x=lambda m: tfd.Sample(tfd.Bernoulli(logits=m), 12),
))
joint.sample(seed=random.PRNGKey(0))
{'e': DeviceArray(3.376818, dtype=float32),
'm': DeviceArray(2.5449684, dtype=float32),
'n': DeviceArray(-0.6027825, dtype=float32),
'x': DeviceArray([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int32)}
Root = tfd.JointDistributionCoroutine.Root
def model():
e = yield Root(tfd.Exponential(rate=1.))
n = yield Root(tfd.Normal(loc=0, scale=2.))
m = yield tfd.Normal(loc=n, scale=e)
x = yield tfd.Sample(tfd.Bernoulli(logits=m), 12)
joint = tfd.JointDistributionCoroutine(model)
joint.sample(seed=random.PRNGKey(0))
StructTuple(var0=DeviceArray(0.17315261, dtype=float32), var1=DeviceArray(-3.290489, dtype=float32), var2=DeviceArray(-3.1949058, dtype=float32), var3=DeviceArray([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], dtype=int32))
অন্যান্য বিতরণ
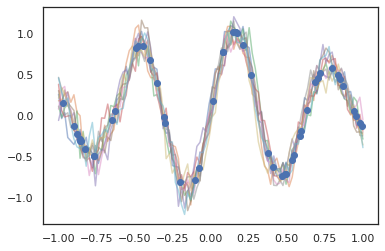
গাউসিয়ান প্রক্রিয়াগুলি JAX মোডেও কাজ করে!
k1, k2, k3 = random.split(random.PRNGKey(0), 3)
observation_noise_variance = 0.01
f = lambda x: jnp.sin(10*x[..., 0]) * jnp.exp(-x[..., 0]**2)
observation_index_points = random.uniform(
k1, [50], minval=-1.,maxval= 1.)[..., jnp.newaxis]
observations = f(observation_index_points) + tfd.Normal(
loc=0., scale=jnp.sqrt(observation_noise_variance)).sample(seed=k2)
index_points = jnp.linspace(-1., 1., 100)[..., jnp.newaxis]
kernel = tfpk.ExponentiatedQuadratic(length_scale=0.1)
gprm = tfd.GaussianProcessRegressionModel(
kernel=kernel,
index_points=index_points,
observation_index_points=observation_index_points,
observations=observations,
observation_noise_variance=observation_noise_variance)
samples = gprm.sample(10, seed=k3)
for i in range(10):
plt.plot(index_points, samples[i], alpha=0.5)
plt.plot(observation_index_points, observations, marker='o', linestyle='')
plt.show()
লুকানো মার্কভ মডেলগুলিও সমর্থিত।
initial_distribution = tfd.Categorical(probs=[0.8, 0.2])
transition_distribution = tfd.Categorical(probs=[[0.7, 0.3],
[0.2, 0.8]])
observation_distribution = tfd.Normal(loc=[0., 15.], scale=[5., 10.])
model = tfd.HiddenMarkovModel(
initial_distribution=initial_distribution,
transition_distribution=transition_distribution,
observation_distribution=observation_distribution,
num_steps=7)
print(model.mean())
print(model.log_prob(jnp.zeros(7)))
print(model.sample(seed=random.PRNGKey(0)))
[3. 6. 7.5 8.249999 8.625001 8.812501 8.90625 ] /usr/local/lib/python3.6/dist-packages/tensorflow_probability/substrates/jax/distributions/hidden_markov_model.py:483: UserWarning: HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug in which the transition model was applied prior to the initial step. This bug has been fixed. You may observe a slight change in behavior. 'HiddenMarkovModel.log_prob in TFP versions < 0.12.0 had a bug ' -19.855635 [ 1.3641367 0.505798 1.3626463 3.6541772 2.272286 15.10309 22.794212 ]
মত কয়েক ডিস্ট্রিবিউশন PixelCNN TensorFlow বা XLA অসামঞ্জস্যপূর্ণ যথাযথ নির্ভরতা কারণে এখনো সমর্থিত নয়।
বিজেক্টর
TFP-এর বেশিরভাগ বিজেক্টর আজ JAX-এ সমর্থিত!
tfb.Exp().inverse(1.)
DeviceArray(0., dtype=float32)
bij = tfb.Shift(1.)(tfb.Scale(3.))
print(bij.forward(jnp.ones(5)))
print(bij.inverse(jnp.ones(5)))
[4. 4. 4. 4. 4.] [0. 0. 0. 0. 0.]
b = tfb.FillScaleTriL(diag_bijector=tfb.Exp(), diag_shift=None)
print(b.forward(x=[0., 0., 0.]))
print(b.inverse(y=[[1., 0], [.5, 2]]))
[[1. 0.] [0. 1.]] [0.6931472 0.5 0. ]
b = tfb.Chain([tfb.Exp(), tfb.Softplus()])
# or:
# b = tfb.Exp()(tfb.Softplus())
print(b.forward(-jnp.ones(5)))
[1.3678794 1.3678794 1.3678794 1.3678794 1.3678794]
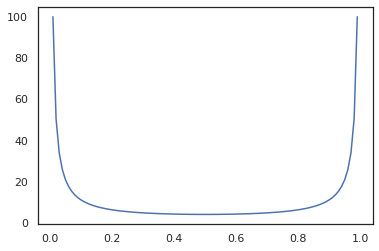
Bijectors মত Jax রূপান্তরের সঙ্গে সামঞ্জস্যপূর্ণ jit , grad এবং vmap ।
jit(vmap(tfb.Exp().inverse))(jnp.arange(4.))
DeviceArray([ -inf, 0. , 0.6931472, 1.0986123], dtype=float32)
x = jnp.linspace(0., 1., 100)
plt.plot(x, jit(grad(lambda x: vmap(tfb.Sigmoid().inverse)(x).sum()))(x))
plt.show()
কিছু bijectors মত RealNVP এবং FFJORD এখনো সমর্থিত নয়।
এমসিএমসি
আমরা বৈশিষ্ট্যসমূহ নিয়ে আসা করেছি tfp.mcmc পাশাপাশি Jax, তাই আমরা হ্যামিল্টনিয়ান মন্টে কার্লো (ক্ষেত্রে HMC) এবং Jax কোন-ইউ-টার্ন-sampler (পাগল) -এর মত আলগোরিদিম রান করতে পারেন।
target_log_prob = tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)).log_prob
TFP মেমরি উপর ভিন্ন, আমরা একটি পাস করার প্রয়োজন হয় PRNGKey মধ্যে sample_chain ব্যবহার seed শব্দ যুক্তি।
def run_chain(key, state):
kernel = tfp.mcmc.NoUTurnSampler(target_log_prob, 1e-1)
return tfp.mcmc.sample_chain(1000,
current_state=state,
kernel=kernel,
trace_fn=lambda _, results: results.target_log_prob,
seed=key)
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros(2))
plt.figure()
plt.scatter(*states.T, alpha=0.5)
plt.figure()
plt.plot(log_probs)
plt.show()
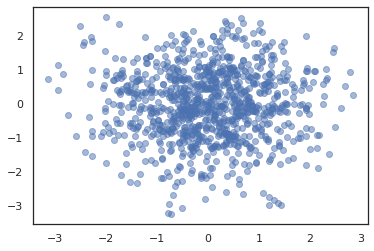
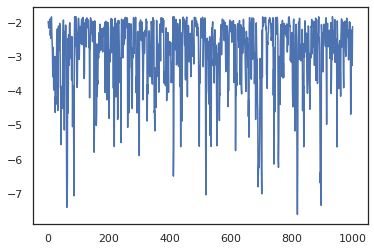
একাধিক চেইন চালানোর জন্য, আমরা হয় রাজ্যের একটি ব্যাচ মধ্যে পাস করতে পারেন sample_chain বা ব্যবহারের vmap (যদিও আমরা এখনো দুটি মধ্যে কর্মক্ষমতা পার্থক্য অন্বেষণ করেন নি)।
states, log_probs = jit(run_chain)(random.PRNGKey(0), jnp.zeros([10, 2]))
plt.figure()
for i in range(10):
plt.scatter(*states[:, i].T, alpha=0.5)
plt.figure()
for i in range(10):
plt.plot(log_probs[:, i], alpha=0.5)
plt.show()
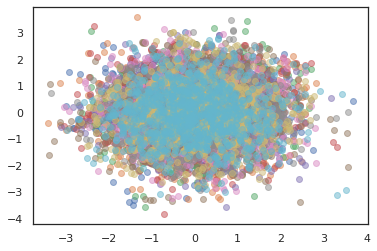
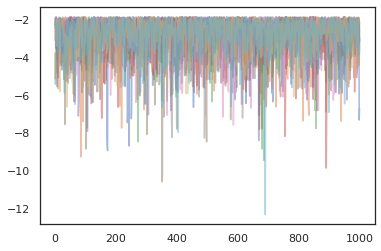
অপ্টিমাইজার
JAX-এ TFP কিছু গুরুত্বপূর্ণ অপ্টিমাইজারকে সমর্থন করে যেমন BFGS এবং L-BFGS। চলুন একটি সহজ স্কেল করা দ্বিঘাতিক ক্ষতি ফাংশন সেট আপ করা যাক।
minimum = jnp.array([1.0, 1.0]) # The center of the quadratic bowl.
scales = jnp.array([2.0, 3.0]) # The scales along the two axes.
# The objective function and the gradient.
def quadratic_loss(x):
return jnp.sum(scales * jnp.square(x - minimum))
start = jnp.array([0.6, 0.8]) # Starting point for the search.
BFGS এই ক্ষতির সর্বনিম্ন খুঁজে পেতে পারে।
optim_results = tfp.optimizer.bfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
তাই L-BFGS করতে পারেন।
optim_results = tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
# Check that the search converged
assert(optim_results.converged)
# Check that the argmin is close to the actual value.
np.testing.assert_allclose(optim_results.position, minimum)
# Print out the total number of function evaluations it took. Should be 5.
print("Function evaluations: %d" % optim_results.num_objective_evaluations)
Function evaluations: 5
করতে vmap , L-BFGS, এর সেট একটি ফাংশন একটি একক আদ্যস্থল জন্য ক্ষতির সেরা অনুকূল রূপ আপ যাক।
def optimize_single(start):
return tfp.optimizer.lbfgs_minimize(
value_and_grad(quadratic_loss), initial_position=start, tolerance=1e-8)
all_results = jit(vmap(optimize_single))(
random.normal(random.PRNGKey(0), (10, 2)))
assert all(all_results.converged)
for i in range(10):
np.testing.assert_allclose(optim_results.position[i], minimum)
print("Function evaluations: %s" % all_results.num_objective_evaluations)
Function evaluations: [6 6 9 6 6 8 6 8 5 9]
সতর্কতা
TF এবং JAX এর মধ্যে কিছু মৌলিক পার্থক্য রয়েছে, কিছু TFP আচরণ দুটি সাবস্ট্রেটের মধ্যে আলাদা হবে এবং সমস্ত কার্যকারিতা সমর্থিত নয়। উদাহরণ স্বরূপ,
- TFP Jax উপর ভালো কিছু সমর্থন করে না
tf.Variableকিছুই যেহেতু মত Jax বিদ্যমান। এই অর্থ মত ইউটিলিটিtfp.util.TransformedVariableপারেন সমর্থিত নয়। -
tfp.layersউপর Keras এবং তার নির্ভরতা কারণে এখনো ব্যাকএন্ড সমর্থিত নয়,tf.Variableগুলি। -
tfp.math.minimizeতার নির্ভরতা কারণ Jax উপর TFP কাজ করে নাtf.Variable। - JAX-এ TFP-এর সাথে, টেনসরের আকারগুলি সর্বদা কংক্রিট পূর্ণসংখ্যার মান এবং TF-তে TFP-এর মতো কখনই অজানা/গতিশীল নয়।
- TF এবং JAX-এ (পরিশিষ্ট দেখুন) সিউডোর্যান্ডমনেস ভিন্নভাবে পরিচালিত হয়।
- মধ্যে লাইব্রেরি
tfp.experimentalJax স্তর মধ্যে উপস্থিত নিশ্চয়তা নেই। - Dtype প্রচারের নিয়মগুলি TF এবং JAX এর মধ্যে আলাদা৷ JAX-এ TFP সামঞ্জস্যের জন্য TF-এর dtype শব্দার্থকে অভ্যন্তরীণভাবে সম্মান করার চেষ্টা করে।
- Bijectors এখনও JAX pytrees হিসাবে নিবন্ধিত করা হয়নি.
কি Jax উপর TFP সমর্থিত সম্পূর্ণ তালিকা দেখতে, দয়া করে পড়ুন এপিআই ডকুমেন্টেশন ।
উপসংহার
আমরা JAX-এ TFP-এর অনেক বৈশিষ্ট্য পোর্ট করেছি এবং সবাই কী তৈরি করবে তা দেখতে আগ্রহী। কিছু কার্যকারিতা এখনও সমর্থিত নয়; আমরা কিছু আপনার কাছে গুরুত্বপূর্ণ মিস করেছি করেন (অথবা যদি আপনি একটি বাগ খুঁজে!) আমাদের কাছে পৌঁছাতে দয়া করে - আপনি ইমেইল করতে পারেন tfprobability@tensorflow.org বা একটি বিষয় দায়ের আমাদের গিটহাব রেপো ।
পরিশিষ্ট: JAX-এ সিউডোর্যান্ডমনেস
Jax এর সিউডোরান্ডম সংখ্যা প্রজন্ম (PRNG) মডেল দেশেরই নাগরিক নয়। একটি রাষ্ট্রীয় মডেলের বিপরীতে, এমন কোনো পরিবর্তনযোগ্য বৈশ্বিক অবস্থা নেই যা প্রতিটি র্যান্ডম ড্রয়ের পরে বিকশিত হয়। Jax এর মডেল, আমরা একটি PRNG কী, যা 32 বিট ইন্টিজার একজোড়া মত কাজ করে দিয়ে শুরু। আমরা ব্যবহার করে এই কী গঠন করা যেতে পারে jax.random.PRNGKey ।
key = random.PRNGKey(0) # Creates a key with value [0, 0]
print(key)
[0 0]
Jax মধ্যে এলোমেলো ফাংশন একটি কী গ্রাস deterministically একটি র্যান্ডম variate উত্পাদন, অর্থাত তারা আবার ব্যবহার করা উচিত নয়। উদাহরণস্বরূপ, আমরা ব্যবহার করতে পারেন key একটি স্বাভাবিকভাবে বিতরণ মান নমুনা, কিন্তু আমরা ব্যবহার করা উচিত নয় key আবার অন্যত্র। অধিকন্তু, একই মান ক্ষণস্থায়ী random.normal একই মান উত্পাদন করা হবে।
print(random.normal(key))
-0.20584226
তাহলে কিভাবে আমরা কখনও একটি একক কী থেকে একাধিক নমুনা আঁকতে পারি? উত্তর কী বিভাজন নেই। মৌলিক ধারণা যে আমরা একটি বিভক্ত করতে পারেন PRNGKey একাধিক মধ্যে, এবং নতুন কী প্রতিটি যদৃচ্ছতা একটি স্বাধীন উৎস হিসেবে গ্রহণ করা যেতে পারে।
key1, key2 = random.split(key, num=2)
print(key1, key2)
[4146024105 967050713] [2718843009 1272950319]
কী বিভাজন নির্ধারক তবে বিশৃঙ্খল, তাই প্রতিটি নতুন কী এখন একটি স্বতন্ত্র র্যান্ডম নমুনা আঁকতে ব্যবহার করা যেতে পারে।
print(random.normal(key1), random.normal(key2))
0.14389051 -1.2515389
Jax এর নির্ণায়ক কী বিভাজন মডেল সম্পর্কে অধিক বিবরণের জন্য, দেখুন এই সহায়িকার ।
