 Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
Tôi viết sổ tay này như một nghiên cứu điển hình để tìm hiểu Xác suất TensorFlow. Vấn đề tôi chọn để giải quyết là ước tính ma trận hiệp phương sai cho các mẫu của biến ngẫu nhiên Gaussian trung bình 2-D. Vấn đề có một vài tính năng hay:
- Nếu chúng ta sử dụng một Wishart nghịch đảo trước cho hiệp phương sai (một cách tiếp cận phổ biến), bài toán có một giải pháp phân tích, vì vậy chúng ta có thể kiểm tra kết quả của mình.
- Vấn đề liên quan đến việc lấy mẫu một tham số bị ràng buộc, điều này làm tăng thêm một số phức tạp thú vị.
- Giải pháp đơn giản nhất không phải là giải pháp nhanh nhất, vì vậy cần phải thực hiện một số công việc tối ưu hóa.
Tôi quyết định viết ra những kinh nghiệm của mình trong quá trình thực hiện. Tôi đã mất một lúc để xoay quanh các điểm tốt hơn của TFP, vì vậy máy tính xách tay này bắt đầu khá đơn giản và sau đó dần dần hoạt động đến các tính năng TFP phức tạp hơn. Tôi đã gặp rất nhiều vấn đề trong quá trình thực hiện và tôi đã cố gắng nắm bắt cả hai quy trình đã giúp tôi xác định chúng và cách giải quyết cuối cùng tôi đã tìm thấy. Tôi đã cố gắng để bao gồm rất nhiều chi tiết (bao gồm rất nhiều các xét nghiệm để đảm bảo bước cá nhân là chính xác).
Tại sao phải học Xác suất TensorFlow?
Tôi thấy Xác suất TensorFlow hấp dẫn cho dự án của mình vì một số lý do:
- Xác suất TensorFlow cho phép bạn phát triển nguyên mẫu các mô hình phức tạp một cách tương tác trong sổ ghi chép. Bạn có thể chia mã của mình thành các phần nhỏ để có thể kiểm tra tương tác và kiểm tra đơn vị.
- Khi bạn đã sẵn sàng mở rộng quy mô, bạn có thể tận dụng tất cả cơ sở hạ tầng mà chúng tôi có sẵn để làm cho TensorFlow chạy trên nhiều bộ xử lý được tối ưu hóa trên nhiều máy.
- Cuối cùng, trong khi tôi thực sự thích Stan, tôi cảm thấy khá khó khăn để gỡ lỗi. Bạn phải viết tất cả mã mô hình của mình bằng một ngôn ngữ độc lập có rất ít công cụ cho phép bạn kiểm tra mã của mình, kiểm tra các trạng thái trung gian, v.v.
Nhược điểm là TensorFlow Probability mới hơn nhiều so với Stan và PyMC3, vì vậy tài liệu đang được tiến hành và có rất nhiều chức năng vẫn chưa được xây dựng. Thật hạnh phúc, tôi thấy nền tảng của TFP là vững chắc và nó được thiết kế theo cách mô-đun cho phép người ta mở rộng chức năng của nó một cách khá đơn giản. Trong sổ tay này, ngoài việc giải quyết nghiên cứu điển hình, tôi sẽ chỉ ra một số cách để mở rộng TFP.
Cái này dành cho ai
Tôi giả định rằng độc giả đến với cuốn sổ này với một số điều kiện tiên quyết quan trọng. Bạn nên:
- Biết những điều cơ bản về suy luận Bayes. (Nếu bạn không, một cuốn sách thật sự tốt đẹp đầu tiên là xét lại thống kê )
- Có quen với một thư viện lấy mẫu MCMC, ví dụ như Stan / PyMC3 / LỖI
- Có một nền tảng vững chắc của NumPy (Một tốt giới thiệu là Python cho phân tích dữ liệu )
- Có ít quen thuộc qua ít nhất là với TensorFlow , nhưng không nhất thiết phải chuyên môn. ( Learning TensorFlow là tốt, nhưng TensorFlow của phương tiện phát triển nhanh chóng mà hầu hết các sách sẽ được một chút ngày. Stanford CS20 tất nhiên cũng là tốt.)
Nỗ lực đầu tiên
Đây là nỗ lực đầu tiên của tôi về vấn đề này. Spoiler: giải pháp của tôi không hiệu quả và sẽ mất vài lần thử để mọi thứ ổn! Mặc dù quá trình này mất một thời gian, nhưng mỗi nỗ lực dưới đây đều hữu ích cho việc học một phần mới của TFP.
Một lưu ý: TFP hiện không triển khai phân phối Wishart nghịch đảo (chúng ta sẽ xem ở phần cuối cách cuộn Wishart nghịch đảo của riêng chúng ta), vì vậy thay vào đó tôi sẽ chuyển vấn đề thành ước tính ma trận chính xác bằng cách sử dụng Wishart trước.
import collections
import math
import os
import time
import numpy as np
import pandas as pd
import scipy
import scipy.stats
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
Bước 1: Thu thập các quan sát cùng nhau
Dữ liệu của tôi ở đây đều là tổng hợp, vì vậy điều này sẽ có vẻ gọn gàng hơn một chút so với một ví dụ trong thế giới thực. Tuy nhiên, không có lý do gì bạn không thể tạo một số dữ liệu tổng hợp của riêng mình.
Mẹo: Khi bạn đã quyết định về hình thức mô hình của bạn, bạn có thể chọn một số giá trị tham số và sử dụng mô hình của bạn được lựa chọn để tạo ra một số dữ liệu tổng hợp. Là một kiểm tra tỉnh táo về việc triển khai của bạn, sau đó bạn có thể xác minh rằng các ước tính của bạn bao gồm các giá trị thực của các thông số bạn đã chọn. Để làm cho chu kỳ gỡ lỗi / thử nghiệm của bạn nhanh hơn, bạn có thể xem xét một phiên bản đơn giản hóa của mô hình của bạn (ví dụ: sử dụng ít kích thước hơn hoặc ít mẫu hơn).
Mẹo: Đó là đơn giản nhất để làm việc với các quan sát của bạn như mảng NumPy. Một điều quan trọng cần lưu ý là NumPy theo mặc định sử dụng float64, trong khi TensorFlow theo mặc định sử dụng float32.
Nói chung, các phép toán TensorFlow muốn tất cả các đối số có cùng kiểu và bạn phải thực hiện truyền dữ liệu rõ ràng để thay đổi kiểu. Nếu bạn sử dụng các quan sát float64, bạn sẽ cần thêm rất nhiều thao tác ép kiểu. Ngược lại, NumPy sẽ tự động xử lý quá trình truyền. Do đó, nó là dễ dàng hơn để chuyển đổi dữ liệu của bạn vào numpy float32 hơn là để buộc TensorFlow để sử dụng float64.
Chọn một số giá trị tham số
# We're assuming 2-D data with a known true mean of (0, 0)
true_mean = np.zeros([2], dtype=np.float32)
# We'll make the 2 coordinates correlated
true_cor = np.array([[1.0, 0.9], [0.9, 1.0]], dtype=np.float32)
# And we'll give the 2 coordinates different variances
true_var = np.array([4.0, 1.0], dtype=np.float32)
# Combine the variances and correlations into a covariance matrix
true_cov = np.expand_dims(np.sqrt(true_var), axis=1).dot(
np.expand_dims(np.sqrt(true_var), axis=1).T) * true_cor
# We'll be working with precision matrices, so we'll go ahead and compute the
# true precision matrix here
true_precision = np.linalg.inv(true_cov)
# Here's our resulting covariance matrix
print(true_cov)
# Verify that it's positive definite, since np.random.multivariate_normal
# complains about it not being positive definite for some reason.
# (Note that I'll be including a lot of sanity checking code in this notebook -
# it's a *huge* help for debugging)
print('eigenvalues: ', np.linalg.eigvals(true_cov))
[[4. 1.8] [1.8 1. ]] eigenvalues: [4.843075 0.15692513]
Tạo một số quan sát tổng hợp
Lưu ý rằng TensorFlow Xác suất sử dụng quy ước rằng kích thước ban đầu (s) của dữ liệu của bạn đại diện cho chỉ số mẫu, và kích thước cuối cùng (s) của dữ liệu của bạn đại diện cho chiều của mẫu của bạn.
Ở đây chúng tôi muốn 100 mẫu, mỗi trong số đó là một vector có độ dài 2. Chúng tôi sẽ tạo ra một mảng my_data với hình dạng (100, 2). my_data[i, :] là \(i\)thứ mẫu, và nó là một vector có độ dài 2.
(Hãy nhớ rằng để làm cho my_data có loại float32!)
# Set the seed so the results are reproducible.
np.random.seed(123)
# Now generate some observations of our random variable.
# (Note that I'm suppressing a bunch of spurious about the covariance matrix
# not being positive semidefinite via check_valid='ignore' because it really is
# positive definite!)
my_data = np.random.multivariate_normal(
mean=true_mean, cov=true_cov, size=100,
check_valid='ignore').astype(np.float32)
my_data.shape
(100, 2)
Sanity kiểm tra các quan sát
Một nguồn lỗi tiềm ẩn đang làm xáo trộn dữ liệu tổng hợp của bạn! Hãy thực hiện một số kiểm tra đơn giản.
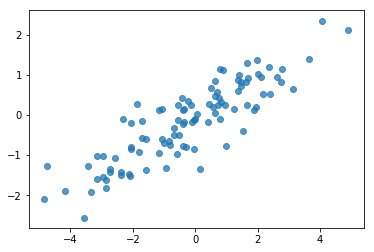
# Do a scatter plot of the observations to make sure they look like what we
# expect (higher variance on the x-axis, y values strongly correlated with x)
plt.scatter(my_data[:, 0], my_data[:, 1], alpha=0.75)
plt.show()
print('mean of observations:', np.mean(my_data, axis=0))
print('true mean:', true_mean)
mean of observations: [-0.24009615 -0.16638893] true mean: [0. 0.]
print('covariance of observations:\n', np.cov(my_data, rowvar=False))
print('true covariance:\n', true_cov)
covariance of observations: [[3.95307734 1.68718486] [1.68718486 0.94910269]] true covariance: [[4. 1.8] [1.8 1. ]]
Ok, các mẫu của chúng tôi trông hợp lý. Bước tiếp theo.
Bước 2: Triển khai chức năng khả năng xảy ra trong NumPy
Điều chính chúng ta cần viết để thực hiện lấy mẫu MCMC của chúng ta trong Xác suất TF là một hàm khả năng xảy ra trong nhật ký. Nói chung, viết TF phức tạp hơn một chút so với NumPy, vì vậy tôi thấy hữu ích khi thực hiện triển khai ban đầu trong NumPy. Tôi sẽ chia các chức năng khả năng thành 2 mảnh, một hàm khả năng dữ liệu tương ứng với \(P(data | parameters)\) và một hàm khả năng trước đó tương ứng với \(P(parameters)\).
Lưu ý rằng các hàm NumPy này không cần phải được tối ưu hóa / vectơ hóa siêu tối ưu vì mục tiêu chỉ là tạo ra một số giá trị để thử nghiệm. Tính đúng đắn là yếu tố cần cân nhắc!
Đầu tiên, chúng tôi sẽ triển khai phần khả năng của nhật ký dữ liệu. Điều đó khá đơn giản. Một điều cần nhớ là chúng ta sẽ làm việc với ma trận chính xác, vì vậy chúng ta sẽ tham số hóa cho phù hợp.
def log_lik_data_numpy(precision, data):
# np.linalg.inv is a really inefficient way to get the covariance matrix, but
# remember we don't care about speed here
cov = np.linalg.inv(precision)
rv = scipy.stats.multivariate_normal(true_mean, cov)
return np.sum(rv.logpdf(data))
# test case: compute the log likelihood of the data given the true parameters
log_lik_data_numpy(true_precision, my_data)
-280.81822950593767
Chúng ta sẽ sử dụng một Wishart trước cho ma trận chính xác kể từ khi có một giải pháp phân tích cho sau (xem bảng tiện dụng Wikipedia của priors liên hợp ).
Các phân phối Wishart có 2 thông số:
- số bậc tự do (nhãn \(\nu\) trong Wikipedia)
- một ma trận quy mô (nhãn \(V\) trong Wikipedia)
Giá trị trung bình cho một phân phối với các thông số Wishart \(\nu, V\) là \(E[W] = \nu V\), và phương sai là \(\text{Var}(W_{ij}) = \nu(v_{ij}^2+v_{ii}v_{jj})\)
Một số trực giác hữu ích: Bạn có thể tạo một mẫu Wishart bằng cách tạo ra \(\nu\) độc lập rút \(x_1 \ldots x_{\nu}\) từ một biến ngẫu nhiên bình thường đa biến với trung bình 0 và phương sai \(V\) và sau đó hình thành tổng \(W = \sum_{i=1}^{\nu} x_i x_i^T\).
Nếu bạn rescale mẫu Wishart bằng cách chia chúng bằng cách \(\nu\), bạn sẽ có được ma trận hiệp phương sai mẫu của \(x_i\). Ma trận hiệp phương sai mẫu này nên có khuynh hướng bộc \(V\) như \(\nu\) tăng. Khi \(\nu\) là nhỏ, có rất nhiều sự thay đổi trong ma trận hiệp phương sai mẫu, giá trị quá nhỏ của \(\nu\) tương ứng với priors yếu và giá trị lớn \(\nu\) tương ứng với priors mạnh. Lưu ý rằng \(\nu\) phải có ít nhất lớn như kích thước của không gian bạn lấy mẫu đang hoặc bạn sẽ tạo ra ma trận duy nhất.
Chúng tôi sẽ sử dụng \(\nu = 3\) vì vậy chúng tôi có một yếu trước, và chúng tôi sẽ \(V = \frac{1}{\nu} I\) mà sẽ kéo ước tính hiệp phương sai của chúng tôi đối với bản sắc (nhớ lại rằng giá trị trung bình là \(\nu V\)).
PRIOR_DF = 3
PRIOR_SCALE = np.eye(2, dtype=np.float32) / PRIOR_DF
def log_lik_prior_numpy(precision):
rv = scipy.stats.wishart(df=PRIOR_DF, scale=PRIOR_SCALE)
return rv.logpdf(precision)
# test case: compute the prior for the true parameters
log_lik_prior_numpy(true_precision)
-9.103606346649766
Sự phân bố Wishart là liên hợp trước để ước lượng ma trận độ chính xác của một bình thường đa biến với tiếng bình \(\mu\).
Giả sử các thông số Wishart trước là \(\nu, V\) và rằng chúng ta có \(n\) quan sát của đa biến bình thường, chúng tôi \(x_1, \ldots, x_n\). Các thông số sau là \(n + \nu, \left(V^{-1} + \sum_{i=1}^n (x_i-\mu)(x_i-\mu)^T \right)^{-1}\).
n = my_data.shape[0]
nu_prior = PRIOR_DF
v_prior = PRIOR_SCALE
nu_posterior = nu_prior + n
v_posterior = np.linalg.inv(np.linalg.inv(v_prior) + my_data.T.dot(my_data))
posterior_mean = nu_posterior * v_posterior
v_post_diag = np.expand_dims(np.diag(v_posterior), axis=1)
posterior_sd = np.sqrt(nu_posterior *
(v_posterior ** 2.0 + v_post_diag.dot(v_post_diag.T)))
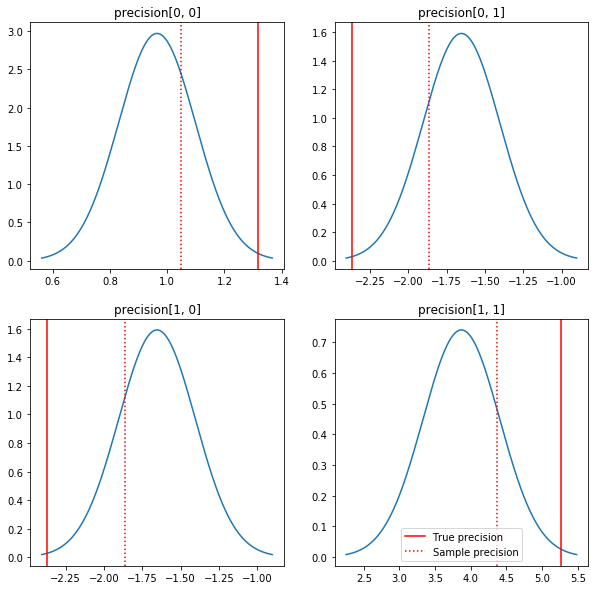
Một sơ đồ ngắn gọn về những điều hậu và các giá trị đích thực. Lưu ý rằng các posteriors gần với posteriors mẫu nhưng bị thu hẹp một chút về phía danh tính. Cũng xin lưu ý rằng các giá trị true khác khá xa so với chế độ của giá trị sau - có lẽ điều này là do giá trị trước không phù hợp lắm với dữ liệu của chúng tôi. Trong một vấn đề thực sự, chúng tôi có khả năng sẽ làm tốt hơn với một cái gì đó giống như một quy mô nghịch đảo Wishart trước cho hiệp phương sai (xem, ví dụ, Andrew Gelman của bài bình luận về đề tài này), nhưng sau đó chúng ta sẽ không có một phân tích sau tốt đẹp.
sample_precision = np.linalg.inv(np.cov(my_data, rowvar=False, bias=False))
fig, axes = plt.subplots(2, 2)
fig.set_size_inches(10, 10)
for i in range(2):
for j in range(2):
ax = axes[i, j]
loc = posterior_mean[i, j]
scale = posterior_sd[i, j]
xmin = loc - 3.0 * scale
xmax = loc + 3.0 * scale
x = np.linspace(xmin, xmax, 1000)
y = scipy.stats.norm.pdf(x, loc=loc, scale=scale)
ax.plot(x, y)
ax.axvline(true_precision[i, j], color='red', label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':', label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.legend()
plt.show()
Bước 3: Triển khai chức năng khả năng trong TensorFlow
Spoiler: Nỗ lực đầu tiên của chúng tôi không thành công; chúng tôi sẽ nói về lý do tại sao bên dưới.
Mẹo: sử dụng TensorFlow háo hức chế độ khi phát triển các chức năng khả năng của bạn. Chế độ háo hức làm TF cư xử giống như NumPy - tất cả mọi thứ thực thi ngay lập tức, vì vậy bạn có thể gỡ lỗi tương tác thay vì phải sử dụng Session.run() . Xem các ghi chú ở đây .
Sơ bộ: Các lớp phân phối
TFP có một tập hợp các lớp phân phối mà chúng tôi sẽ sử dụng để tạo ra xác suất nhật ký của chúng tôi. Một điều cần lưu ý là các lớp này hoạt động với hàng chục mẫu thay vì chỉ các mẫu đơn lẻ - điều này cho phép vectơ hóa và tăng tốc độ liên quan.
Một phân phối có thể hoạt động với hàng chục mẫu theo 2 cách khác nhau. Đơn giản nhất là minh họa 2 cách này bằng một ví dụ cụ thể liên quan đến phân phối với một tham số vô hướng duy nhất. Tôi sẽ sử dụng Poisson phân phối, trong đó có một rate tham số.
- Nếu chúng ta tạo ra một Poisson với một giá trị duy nhất cho
ratetham số, một lời kêu gọi của nósample()phương pháp trả về một giá trị duy nhất. Giá trị này được gọi là mộtevent, và trong trường hợp này các sự kiện đều vô hướng. - Nếu chúng ta tạo ra một Poisson với một tensor của các giá trị cho các
ratetham số, một lời kêu gọi của nósample()phương pháp hiện nay trả về nhiều giá trị, một cho mỗi giá trị trong tensor hạng nhất. Các đối tượng đóng vai trò như một bộ sưu tập của Poissons độc lập, đều có tỷ lệ riêng của mình, và mỗi người trong số các giá trị được trả về bởi một cuộc gọi đếnsample()tương ứng với một trong những Poissons. Bộ sưu tập này của các sự kiện phân phối hệt độc lập nhưng không được gọi làbatch. - Các
sample()phương pháp mất mộtsample_shapetham số mặc định là một tuple trống. Đi qua một giá trị không trống chosample_shapekết quả trong mẫu trở nhiều lô. Bộ sưu tập này của lô được gọi là mộtsample.
Một bản phân phối log_prob() phương pháp tiêu thụ dữ liệu theo cách song song cách sample() tạo ra nó. log_prob() trả về xác suất cho mẫu, tức là cho nhiều, lô độc lập của các sự kiện.
- Nếu chúng ta có đối tượng Poisson của chúng tôi đã được tạo ra với một vô hướng
rate, mỗi lô là một đại lượng vô hướng, và nếu chúng ta vượt qua trong một tensor mẫu, chúng tôi sẽ nhận ra một tensor có cùng kích thước của xác suất log. - Nếu chúng ta có đối tượng Poisson của chúng tôi đã được tạo ra với một tensor của hình
Tcủarategiá trị, mỗi đợt là một tensor của hìnhT. Nếu chúng ta chuyển vào một hàng chục mẫu có hình dạng D, T, chúng ta sẽ nhận được một hàng chục xác suất log của hình dạng D, T.
Dưới đây là một số ví dụ minh họa các trường hợp này. Xem máy tính xách tay này cho một hướng dẫn chi tiết thêm về các sự kiện, lô, và hình dạng.
# case 1: get log probabilities for a vector of iid draws from a single
# normal distribution
norm1 = tfd.Normal(loc=0., scale=1.)
probs1 = norm1.log_prob(tf.constant([1., 0.5, 0.]))
# case 2: get log probabilities for a vector of independent draws from
# multiple normal distributions with different parameters. Note the vector
# values for loc and scale in the Normal constructor.
norm2 = tfd.Normal(loc=[0., 2., 4.], scale=[1., 1., 1.])
probs2 = norm2.log_prob(tf.constant([1., 0.5, 0.]))
print('iid draws from a single normal:', probs1.numpy())
print('draws from a batch of normals:', probs2.numpy())
iid draws from a single normal: [-1.4189385 -1.0439385 -0.9189385] draws from a batch of normals: [-1.4189385 -2.0439386 -8.918939 ]
Khả năng ghi nhật ký dữ liệu
Đầu tiên, chúng tôi sẽ triển khai chức năng khả năng ghi nhật ký dữ liệu.
VALIDATE_ARGS = True
ALLOW_NAN_STATS = False
Một điểm khác biệt chính so với trường hợp NumPy là hàm khả năng TensorFlow của chúng tôi sẽ cần xử lý các vectơ của ma trận chính xác thay vì chỉ ma trận đơn lẻ. Các vectơ tham số sẽ được sử dụng khi chúng tôi lấy mẫu từ nhiều chuỗi.
Chúng tôi sẽ tạo một đối tượng phân phối hoạt động với một loạt ma trận chính xác (tức là một ma trận trên mỗi chuỗi).
Khi tính toán xác suất nhật ký dữ liệu của chúng tôi, chúng tôi sẽ cần dữ liệu của chúng tôi được sao chép theo cách tương tự như các tham số của chúng tôi để có một bản sao cho mỗi biến số lô. Hình dạng của dữ liệu được sao chép của chúng tôi sẽ cần phải như sau:
[sample shape, batch shape, event shape]
Trong trường hợp của chúng tôi, hình dạng sự kiện là 2 (vì chúng tôi đang làm việc với Gaussian 2-D). Hình dạng mẫu là 100, vì chúng tôi có 100 mẫu. Hình dạng lô sẽ chỉ là số lượng ma trận chính xác mà chúng tôi đang làm việc. Thật lãng phí khi sao chép dữ liệu mỗi khi chúng tôi gọi hàm khả năng xảy ra, vì vậy chúng tôi sẽ sao chép dữ liệu trước và chuyển trong phiên bản đã sao chép.
Lưu ý rằng đây là một thực hiện không hiệu quả: MultivariateNormalFullCovariance là tốn kém so với một số lựa chọn thay thế mà chúng ta sẽ nói về trong phần tối ưu hóa ở cuối.
def log_lik_data(precisions, replicated_data):
n = tf.shape(precisions)[0] # number of precision matrices
# We're estimating a precision matrix; we have to invert to get log
# probabilities. Cholesky inversion should be relatively efficient,
# but as we'll see later, it's even better if we can avoid doing the Cholesky
# decomposition altogether.
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# For our test, we'll use a tensor of 2 precision matrices.
# We'll need to replicate our data for the likelihood function.
# Remember, TFP wants the data to be structured so that the sample dimensions
# are first (100 here), then the batch dimensions (2 here because we have 2
# precision matrices), then the event dimensions (2 because we have 2-D
# Gaussian data). We'll need to add a middle dimension for the batch using
# expand_dims, and then we'll need to create 2 replicates in this new dimension
# using tile.
n = 2
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
print(replicated_data.shape)
(100, 2, 2)
Mẹo: Một điều tôi đã tìm thấy là cực kỳ hữu ích được viết séc sanity ít chức năng TensorFlow tôi. Thực sự rất dễ làm rối quá trình vector hóa trong TF, do đó, có các hàm NumPy đơn giản hơn xung quanh là một cách tuyệt vời để xác minh đầu ra TF. Hãy coi đây là những bài kiểm tra đơn vị nhỏ.
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_data(precisions, replicated_data=replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
Khả năng ghi nhật ký trước
Cái trước dễ dàng hơn vì chúng ta không phải lo lắng về việc sao chép dữ liệu.
@tf.function(autograph=False)
def log_lik_prior(precisions):
rv_precision = tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions)
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_prior(precisions).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]))
print('tensorflow:', lik_tf[i])
0 numpy: -2.2351873809649625 tensorflow: -2.2351875 1 numpy: -9.103606346649766 tensorflow: -9.103608
Xây dựng hàm khả năng ghi nhật ký chung
Hàm khả năng xảy ra trong nhật ký dữ liệu ở trên phụ thuộc vào quan sát của chúng tôi, nhưng trình lấy mẫu sẽ không có những chức năng đó. Chúng ta có thể loại bỏ sự phụ thuộc mà không cần sử dụng biến toàn cục bằng cách sử dụng [bao đóng] (https://en.wikipedia.org/wiki/Closure_ (computer_programming). Đóng bao gồm một hàm bên ngoài xây dựng một môi trường chứa các biến cần thiết bởi một nội hàm.
def get_log_lik(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik(precision):
return log_lik_data(precision, replicated_data) + log_lik_prior(precision)
return _log_lik
Bước 4: Mẫu
Được rồi, đã đến lúc lấy mẫu! Để giữ cho mọi thứ đơn giản, chúng tôi sẽ chỉ sử dụng 1 chuỗi và chúng tôi sẽ sử dụng ma trận nhận dạng làm điểm bắt đầu. Chúng tôi sẽ làm mọi thứ cẩn thận hơn sau.
Một lần nữa, điều này sẽ không hoạt động - chúng tôi sẽ có một ngoại lệ.
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.expand_dims(tf.eye(2), axis=0)
# Use expand_dims because we want to pass in a tensor of starting values
log_lik_fn = get_log_lik(my_data, n_chains=1)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
return states
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
Cholesky decomposition was not successful. The input might not be valid.
[[{ {node mcmc_sample_chain/trace_scan/while/body/_79/smart_for_loop/while/body/_371/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_537/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/StatefulPartitionedCall/Cholesky} }]] [Op:__inference_sample_2849]
Function call stack:
sample
...
Function call stack:
sample
Xác định vấn đề
InvalidArgumentError (see above for traceback): Cholesky decomposition was not successful. The input might not be valid. Đó không phải là siêu hữu ích. Hãy xem nếu chúng ta có thể tìm hiểu thêm về những gì đã xảy ra.
- Chúng tôi sẽ in ra các thông số cho từng bước để chúng tôi có thể thấy giá trị mà những thứ không thành công
- Chúng tôi sẽ thêm một số xác nhận để đề phòng các vấn đề cụ thể.
Các xác nhận rất phức tạp vì chúng là các hoạt động TensorFlow và chúng tôi phải cẩn thận để chúng được thực thi và không được tối ưu hóa ra khỏi biểu đồ. Nó đáng đọc cái nhìn tổng quan này của TensorFlow gỡ lỗi nếu bạn không quen thuộc với khẳng định TF. Bạn có thể buộc một cách rõ ràng khẳng định để thực hiện sử dụng tf.control_dependencies (xem các chú thích trong mã bên dưới).
Mẹ đẻ TensorFlow của Print hàm có hành vi tương tự như khẳng định - đó là một hoạt động, và bạn cần phải thực hiện một số dịch vụ chăm sóc để đảm bảo rằng nó thực thi. Print gây đau đầu bổ sung khi chúng tôi đang làm việc trong một máy tính xách tay: sản lượng của nó sẽ được gửi đến stderr , và stderr không được hiển thị trong các tế bào. Chúng tôi sẽ sử dụng một thủ thuật ở đây: thay vì sử dụng tf.Print , chúng ta sẽ tạo hoạt động TensorFlow in riêng của chúng tôi qua tf.pyfunc . Đối với các xác nhận, chúng ta phải đảm bảo rằng phương thức của chúng ta thực thi.
def get_log_lik_verbose(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
def _log_lik(precisions):
# An internal method we'll make into a TensorFlow operation via tf.py_func
def _print_precisions(precisions):
print('precisions:\n', precisions)
return False # operations must return something!
# Turn our method into a TensorFlow operation
print_op = tf.compat.v1.py_func(_print_precisions, [precisions], tf.bool)
# Assertions are also operations, and some care needs to be taken to ensure
# that they're executed
assert_op = tf.assert_equal(
precisions, tf.linalg.matrix_transpose(precisions),
message='not symmetrical', summarize=4, name='symmetry_check')
# The control_dependencies statement forces its arguments to be executed
# before subsequent operations
with tf.control_dependencies([print_op, assert_op]):
return (log_lik_data(precisions, replicated_data) +
log_lik_prior(precisions))
return _log_lik
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.eye(2)[tf.newaxis, ...]
log_lik_fn = get_log_lik_verbose(my_data)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[ 0.24315196 -0.2761638 ]
[-0.33882257 0.8622 ]]]
assertion failed: [not symmetrical] [Condition x == y did not hold element-wise:] [x (leapfrog_integrate_one_step/add:0) = ] [[[0.243151963 -0.276163787][-0.338822573 0.8622]]] [y (leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/matrix_transpose/transpose:0) = ] [[[0.243151963 -0.338822573][-0.276163787 0.8622]]]
[[{ {node mcmc_sample_chain/trace_scan/while/body/_96/smart_for_loop/while/body/_381/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_503/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/symmetry_check_1/Assert/AssertGuard/else/_577/Assert} }]] [Op:__inference_sample_4837]
Function call stack:
sample
...
Function call stack:
sample
Tại sao điều này không thành công
Giá trị tham số mới đầu tiên mà trình lấy mẫu thử là một ma trận không đối xứng. Điều đó gây ra sự phân rã Cholesky không thành công, vì nó chỉ được xác định cho các ma trận đối xứng (và xác định dương).
Vấn đề ở đây là tham số quan tâm của chúng ta là một ma trận chính xác và ma trận chính xác phải là thực, đối xứng và xác định dương. Trình lấy mẫu không biết bất cứ điều gì về ràng buộc này (ngoại trừ có thể thông qua các gradient), do đó, hoàn toàn có khả năng trình lấy mẫu sẽ đề xuất một giá trị không hợp lệ, dẫn đến một ngoại lệ, đặc biệt nếu kích thước bước lớn.
Với bộ lấy mẫu Hamilton Monte Carlo, chúng tôi có thể giải quyết vấn đề bằng cách sử dụng kích thước bước rất nhỏ, vì gradient sẽ giữ các tham số tránh xa các vùng không hợp lệ, nhưng kích thước bước nhỏ có nghĩa là hội tụ chậm. Với một bộ lấy mẫu Metropolis-Hastings, không biết gì về độ dốc, chúng ta sẽ chết.
Phiên bản 2: đo lường lại thành các tham số không bị giới hạn
Có một giải pháp đơn giản cho vấn đề ở trên: chúng ta có thể đánh giá lại mô hình của mình để các tham số mới không còn những ràng buộc này nữa. TFP cung cấp một bộ công cụ hữu ích - bijector - để thực hiện điều đó.
Tái phản ứng với bijector
Ma trận chính xác của chúng tôi phải là thực và đối xứng; chúng tôi muốn một tham số hóa thay thế không có những ràng buộc này. Điểm bắt đầu là phép nhân tử hóa Cholesky của ma trận chính xác. Các yếu tố Cholesky vẫn bị hạn chế - chúng có hình tam giác thấp hơn và các yếu tố đường chéo của chúng phải dương. Tuy nhiên, nếu chúng ta lấy nhật ký các đường chéo của thừa số Cholesky, thì các nhật ký không còn bị ràng buộc là dương nữa, và sau đó nếu chúng ta làm phẳng phần hình tam giác dưới thành vectơ 1-D, chúng ta không còn bị ràng buộc tam giác dưới nữa. . Kết quả trong trường hợp của chúng ta sẽ là một vectơ độ dài 3 không có ràng buộc.
(Các thủ Stan có một chương lớn về việc sử dụng biến đổi để loại bỏ nhiều loại hình khó khăn về thông số.)
Việc tham số lại này ít ảnh hưởng đến hàm khả năng ghi nhật ký dữ liệu của chúng ta - chúng ta chỉ cần đảo ngược phép biến đổi để lấy lại ma trận chính xác - nhưng ảnh hưởng đối với ma trận trước phức tạp hơn. Chúng tôi đã xác định rằng xác suất của một ma trận chính xác nhất định được đưa ra bởi phân phối Wishart; xác suất của ma trận được biến đổi của chúng ta là bao nhiêu?
Nhớ lại rằng nếu chúng ta áp dụng một hàm số đơn điệu \(g\) để 1-D biến ngẫu nhiên \(X\), \(Y = g(X)\), mật độ cho \(Y\) được cho bởi
\[ f_Y(y) = | \frac{d}{dy}(g^{-1}(y)) | f_X(g^{-1}(y)) \]
Đạo hàm của \(g^{-1}\) hạn chiếm cách mà \(g\) thay đổi khối lượng của địa phương. Đối với biến ngẫu nhiên chiều cao, yếu tố điều chỉnh là giá trị tuyệt đối của yếu tố quyết định của Jacobian của \(g^{-1}\) (xem ở đây ).
Chúng ta sẽ phải thêm một Jacobian của phép biến đổi nghịch đảo vào hàm khả năng xảy ra trước nhật ký của chúng ta. Hạnh phúc, TFP của Bijector lớp có thể chăm sóc này cho chúng tôi.
Các Bijector lớp được sử dụng để đại diện cho khả nghịch, chức năng mượt mà được sử dụng để thay đổi các biến trong hàm mật độ xác suất. Bijectors tất cả đều có một forward() phương pháp mà thực hiện một chuyển đổi, một inverse() phương pháp đó sẽ đảo ngược nó, và forward_log_det_jacobian() và inverse_log_det_jacobian() phương pháp mà cung cấp các điều chỉnh Jacobian chúng ta cần khi chúng ta reparaterize một pdf.
TFP cung cấp một tập hợp các bijectors hữu ích mà chúng ta có thể kết hợp thông qua thành phần thông qua các Chain nhà điều hành để tạo thành biến đổi khá phức tạp. Trong trường hợp của chúng tôi, chúng tôi sẽ tạo 3 bijector sau (các hoạt động trong chuỗi được thực hiện từ phải sang trái):
- Bước đầu tiên của phép biến đổi của chúng ta là thực hiện phép phân tích nhân tử Cholesky trên ma trận chính xác. Không có lớp Bijector cho điều đó; Tuy nhiên, các
CholeskyOuterProductbijector mất sản phẩm của 2 yếu tố Cholesky. Chúng ta có thể sử dụng nghịch đảo của mà hoạt động bằng cách sử dụngInvertđiều hành. - Bước tiếp theo là lấy nhật ký của các yếu tố đường chéo của yếu tố Cholesky. Chúng tôi thực hiện điều này thông qua
TransformDiagonalbijector và nghịch đảo củaExpbijector. - Cuối cùng chúng tôi làm phẳng phần tam giác dưới của ma trận để một vector sử dụng nghịch đảo của
FillTriangularbijector.
# Our transform has 3 stages that we chain together via composition:
precision_to_unconstrained = tfb.Chain([
# step 3: flatten the lower triangular portion of the matrix
tfb.Invert(tfb.FillTriangular(validate_args=VALIDATE_ARGS)),
# step 2: take the log of the diagonals
tfb.TransformDiagonal(tfb.Invert(tfb.Exp(validate_args=VALIDATE_ARGS))),
# step 1: decompose the precision matrix into its Cholesky factors
tfb.Invert(tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS)),
])
# sanity checks
m = tf.constant([[1., 2.], [2., 8.]])
m_fwd = precision_to_unconstrained.forward(m)
m_inv = precision_to_unconstrained.inverse(m_fwd)
# bijectors handle tensors of values, too!
m2 = tf.stack([m, tf.eye(2)])
m2_fwd = precision_to_unconstrained.forward(m2)
m2_inv = precision_to_unconstrained.inverse(m2_fwd)
print('single input:')
print('m:\n', m.numpy())
print('precision_to_unconstrained(m):\n', m_fwd.numpy())
print('inverse(precision_to_unconstrained(m)):\n', m_inv.numpy())
print()
print('tensor of inputs:')
print('m2:\n', m2.numpy())
print('precision_to_unconstrained(m2):\n', m2_fwd.numpy())
print('inverse(precision_to_unconstrained(m2)):\n', m2_inv.numpy())
single input: m: [[1. 2.] [2. 8.]] precision_to_unconstrained(m): [0.6931472 2. 0. ] inverse(precision_to_unconstrained(m)): [[1. 2.] [2. 8.]] tensor of inputs: m2: [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]] precision_to_unconstrained(m2): [[0.6931472 2. 0. ] [0. 0. 0. ]] inverse(precision_to_unconstrained(m2)): [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]]
Các TransformedDistribution lớp tự động hóa quá trình áp dụng một bijector với phân phối và làm cho việc sửa Jacobian cần thiết để log_prob() . Trước đó mới của chúng tôi trở thành:
def log_lik_prior_transformed(transformed_precisions):
rv_precision = tfd.TransformedDistribution(
tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS),
bijector=precision_to_unconstrained,
validate_args=VALIDATE_ARGS)
return rv_precision.log_prob(transformed_precisions)
# Check against the numpy implementation. Note that when comparing, we need
# to add in the Jacobian correction.
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_prior_transformed(transformed_precisions).numpy()
corrections = precision_to_unconstrained.inverse_log_det_jacobian(
transformed_precisions, event_ndims=1).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow: -0.84889317 1 numpy: -7.305657151741624 tensorflow: -7.305659
Chúng tôi chỉ cần đảo ngược chuyển đổi để có khả năng ghi nhật ký dữ liệu của chúng tôi:
precision = precision_to_unconstrained.inverse(transformed_precision)
Vì chúng tôi thực sự muốn nhân tử hóa Cholesky của ma trận chính xác, sẽ hiệu quả hơn nếu chỉ thực hiện một phần nghịch đảo ở đây. Tuy nhiên, chúng tôi sẽ để lại phần tối ưu hóa cho phần sau và sẽ để phần nghịch đảo như một bài tập cho người đọc.
def log_lik_data_transformed(transformed_precisions, replicated_data):
# We recover the precision matrix by inverting our bijector. This is
# inefficient since we really want the Cholesky decomposition of the
# precision matrix, and the bijector has that in hand during the inversion,
# but we'll worry about efficiency later.
n = tf.shape(transformed_precisions)[0]
precisions = precision_to_unconstrained.inverse(transformed_precisions)
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# sanity check
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_data_transformed(
transformed_precisions, replicated_data).numpy()
for i in range(precisions.shape[0]):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
Một lần nữa, chúng tôi kết thúc các chức năng mới của chúng tôi trong một lần đóng cửa.
def get_log_lik_transformed(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_transformed(transformed_precisions):
return (log_lik_data_transformed(transformed_precisions, replicated_data) +
log_lik_prior_transformed(transformed_precisions))
return _log_lik_transformed
# make sure everything runs
log_lik_fn = get_log_lik_transformed(my_data)
m = tf.eye(2)[tf.newaxis, ...]
lik = log_lik_fn(precision_to_unconstrained.forward(m)).numpy()
print(lik)
[-431.5611]
Lấy mẫu
Bây giờ chúng ta không phải lo lắng về việc bộ lấy mẫu của chúng ta bị nổ tung vì các giá trị tham số không hợp lệ, hãy tạo một số mẫu thực.
Trình lấy mẫu hoạt động với phiên bản không bị giới hạn của các tham số của chúng tôi, vì vậy chúng tôi cần chuyển đổi giá trị ban đầu của mình thành phiên bản không bị giới hạn của nó. Các mẫu mà chúng tôi tạo ra cũng sẽ ở dạng không bị hạn chế, vì vậy chúng tôi cần phải biến đổi chúng trở lại. Bijector được vectơ hóa, vì vậy rất dễ làm như vậy.
# We'll choose a proper random initial value this time
np.random.seed(123)
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_value = initial_value_cholesky.dot(
initial_value_cholesky.T)[np.newaxis, ...]
# The sampler works with unconstrained values, so we'll transform our initial
# value
initial_value_transformed = precision_to_unconstrained.forward(
initial_value).numpy()
# Sample!
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data, n_chains=1)
num_results = 1000
num_burnin_steps = 1000
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
initial_value_transformed,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=lambda _, pkr: pkr.is_accepted,
seed=123)
# transform samples back to their constrained form
precision_samples = [precision_to_unconstrained.inverse(s) for s in states]
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
Hãy so sánh giá trị trung bình của đầu ra của trình lấy mẫu với giá trị trung bình sau phân tích!
print('True posterior mean:\n', posterior_mean)
print('Sample mean:\n', np.mean(np.reshape(precision_samples, [-1, 2, 2]), axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Sample mean: [[ 1.4315274 -0.25587553] [-0.25587553 0.5740424 ]]
Chúng ta đang đi! Hãy tìm hiểu lý do tại sao. Đầu tiên chúng ta hãy nhìn vào các mẫu của chúng tôi.
np.reshape(precision_samples, [-1, 2, 2])
array([[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
...,
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]]], dtype=float32)
Rất tiếc - có vẻ như tất cả chúng đều có giá trị như nhau. Hãy tìm hiểu lý do tại sao.
Các kernel_results_ biến là một tuple tên đó cung cấp thông tin về các mẫu tại mỗi tiểu bang. Các is_accepted lĩnh vực là chìa khóa ở đây.
# Look at the acceptance for the last 100 samples
print(np.squeeze(is_accepted)[-100:])
print('Fraction of samples accepted:', np.mean(np.squeeze(is_accepted)))
[False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False] Fraction of samples accepted: 0.0
Tất cả các mẫu của chúng tôi đã bị từ chối! Có lẽ kích thước bước của chúng tôi quá lớn. Tôi chọn stepsize=0.1 hoàn toàn tùy tiện.
Phiên bản 3: lấy mẫu với kích thước bước thích ứng
Vì việc lấy mẫu với lựa chọn kích thước bước tùy ý của tôi không thành công, chúng tôi có một số mục trong chương trình làm việc:
- triển khai kích thước bước thích ứng và
- thực hiện một số kiểm tra độ hội tụ.
Có một số mẫu mã đẹp trong tensorflow_probability/python/mcmc/hmc.py để thực hiện kích thước bước thích nghi. Tôi đã điều chỉnh nó dưới đây.
Lưu ý rằng có một riêng biệt sess.run() tuyên bố cho mỗi bước. Điều này thực sự hữu ích cho việc gỡ lỗi, vì nó cho phép chúng tôi dễ dàng thêm một số chẩn đoán theo từng bước nếu cần. Ví dụ: chúng tôi có thể hiển thị tiến trình tăng dần, thời gian từng bước, v.v.
Mẹo: Một cách rõ ràng thông thường để mess up lấy mẫu của bạn là phải có nuôi đồ thị của bạn trong vòng lặp. (Lý do để hoàn thiện biểu đồ trước khi phiên chạy là để ngăn chặn những vấn đề như vậy.) Tuy nhiên, nếu bạn chưa sử dụng finalize (), hãy kiểm tra gỡ lỗi hữu ích nếu mã của bạn chậm thu thập thông tin là in ra biểu đồ kích thước ở mỗi bước qua len(mygraph.get_operations()) - nếu tăng chiều dài, có lẽ bạn đang làm điều gì xấu.
Chúng tôi sẽ chạy 3 chuỗi độc lập ở đây. Thực hiện một số so sánh giữa các chuỗi sẽ giúp chúng tôi kiểm tra sự hội tụ.
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values = []
for i in range(N_CHAINS):
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_values.append(initial_value_cholesky.dot(initial_value_cholesky.T))
initial_values = np.stack(initial_values)
initial_values_transformed = precision_to_unconstrained.forward(
initial_values).numpy()
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=hmc,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values_transformed,
kernel=adapted_kernel,
trace_fn=lambda _, pkr: pkr.inner_results.is_accepted,
parallel_iterations=1)
# transform samples back to their constrained form
precision_samples = precision_to_unconstrained.inverse(states)
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
Kiểm tra nhanh: tỷ lệ chấp nhận của chúng tôi trong quá trình lấy mẫu của chúng tôi gần với mục tiêu của chúng tôi là 0,651.
print(np.mean(is_accepted))
0.6190666666666667
Tốt hơn nữa, trung bình mẫu và độ lệch chuẩn của chúng tôi gần với những gì chúng tôi mong đợi từ giải pháp phân tích.
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96426415 -1.6519215 ] [-1.6519215 3.8614824 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13622096 0.25235635] [0.25235635 0.5394968 ]]
Kiểm tra sự hội tụ
Nói chung, chúng tôi sẽ không có giải pháp phân tích để kiểm tra, vì vậy chúng tôi cần đảm bảo rằng bộ lấy mẫu đã hội tụ. Một kiểm tra tiêu chuẩn là Gelman-Rubin \(\hat{R}\) Thống kê, đòi hỏi nhiều chuỗi mẫu. \(\hat{R}\) biện pháp mức độ mà phương sai (trong những phương tiện) giữa chuỗi vượt quá những gì người ta mong chờ nếu chuỗi được phân phối hệt. Giá trị của \(\hat{R}\) gần 1 được sử dụng để chỉ hội tụ tương đối. Xem nguồn để biết chi tiết.
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0038308 1.0005717] [1.0005717 1.0006068]]
Phê bình mô hình
Nếu chúng ta không có một giải pháp phân tích, đây sẽ là lúc để thực hiện một số chỉ trích về mô hình thực tế.
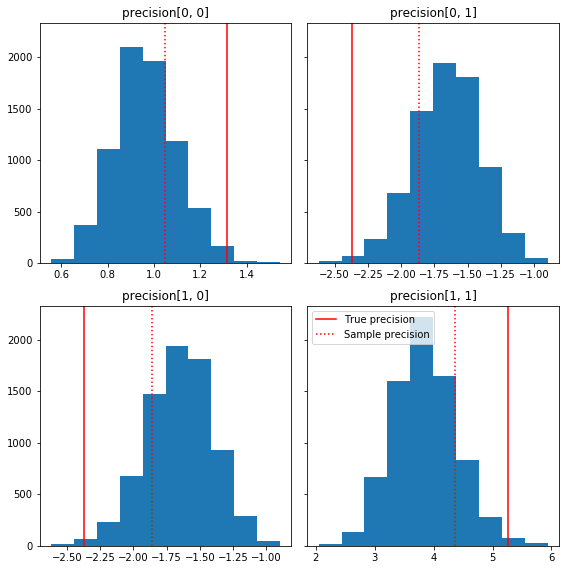
Dưới đây là một vài biểu đồ nhanh của các thành phần mẫu liên quan đến sự thật cơ bản của chúng tôi (màu đỏ). Lưu ý rằng các mẫu đã được thu nhỏ từ các giá trị ma trận độ chính xác của mẫu về ma trận nhận dạng trước đó.
fig, axes = plt.subplots(2, 2, sharey=True)
fig.set_size_inches(8, 8)
for i in range(2):
for j in range(2):
ax = axes[i, j]
ax.hist(precision_samples_reshaped[:, i, j])
ax.axvline(true_precision[i, j], color='red',
label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':',
label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.tight_layout()
plt.legend()
plt.show()
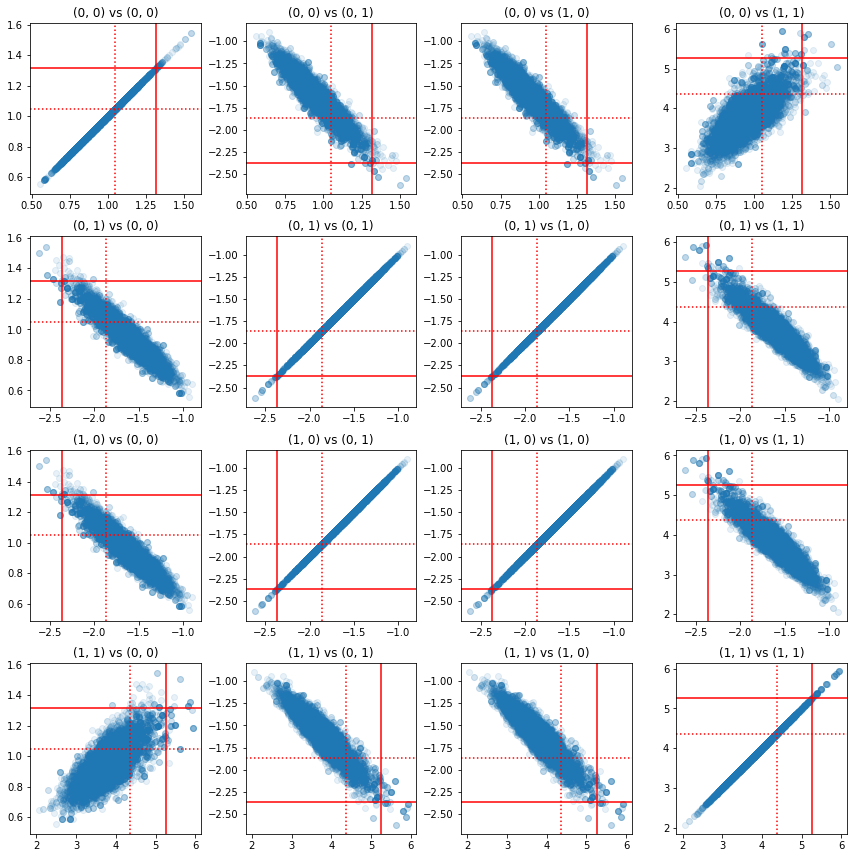
Một số biểu đồ phân tán của các cặp thành phần chính xác cho thấy rằng do cấu trúc tương quan của phần sau, các giá trị thực sau không khó xảy ra như chúng xuất hiện từ các biên ở trên.
fig, axes = plt.subplots(4, 4)
fig.set_size_inches(12, 12)
for i1 in range(2):
for j1 in range(2):
index1 = 2 * i1 + j1
for i2 in range(2):
for j2 in range(2):
index2 = 2 * i2 + j2
ax = axes[index1, index2]
ax.scatter(precision_samples_reshaped[:, i1, j1],
precision_samples_reshaped[:, i2, j2], alpha=0.1)
ax.axvline(true_precision[i1, j1], color='red')
ax.axhline(true_precision[i2, j2], color='red')
ax.axvline(sample_precision[i1, j1], color='red', linestyle=':')
ax.axhline(sample_precision[i2, j2], color='red', linestyle=':')
ax.set_title('(%d, %d) vs (%d, %d)' % (i1, j1, i2, j2))
plt.tight_layout()
plt.show()
Phiên bản 4: Lấy mẫu đơn giản hơn các tham số bị ràng buộc
Bijector làm cho việc lấy mẫu ma trận chính xác trở nên đơn giản, nhưng có rất nhiều thao tác chuyển đổi thủ công đến và từ biểu diễn không bị giới hạn. Co một cach dê dang hơn!
Hạt nhân TransformedTransition
Các TransformedTransitionKernel đơn giản hoá quá trình này. Nó bao bọc trình lấy mẫu của bạn và xử lý tất cả các chuyển đổi. Nó coi như một đối số là danh sách các bijector ánh xạ các giá trị tham số không bị giới hạn thành các giá trị bị ràng buộc. Vì vậy, ở đây chúng ta cần nghịch đảo của precision_to_unconstrained bijector chúng tôi sử dụng trên. Chúng tôi chỉ có thể sử dụng tfb.Invert(precision_to_unconstrained) , nhưng điều đó sẽ liên quan đến việc các phần tử nghịch đảo của phần tử nghịch đảo (TensorFlow không đủ thông minh để đơn giản hóa tf.Invert(tf.Invert()) để tf.Identity()) , nên thay vì chúng ta Tôi sẽ chỉ viết một bijector mới.
Ràng buộc bijector
# The bijector we need for the TransformedTransitionKernel is the inverse of
# the one we used above
unconstrained_to_precision = tfb.Chain([
# step 3: take the product of Cholesky factors
tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS),
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: map a vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# quick sanity check
m = [[1., 2.], [2., 8.]]
m_inv = unconstrained_to_precision.inverse(m).numpy()
m_fwd = unconstrained_to_precision.forward(m_inv).numpy()
print('m:\n', m)
print('unconstrained_to_precision.inverse(m):\n', m_inv)
print('forward(unconstrained_to_precision.inverse(m)):\n', m_fwd)
m: [[1.0, 2.0], [2.0, 8.0]] unconstrained_to_precision.inverse(m): [0.6931472 2. 0. ] forward(unconstrained_to_precision.inverse(m)): [[1. 2.] [2. 8.]]
Lấy mẫu với TransformedTransitionKernel
Với TransformedTransitionKernel , chúng ta không còn phải làm biến đổi thủ công các thông số của chúng tôi. Các giá trị ban đầu và các mẫu của chúng tôi đều là ma trận chính xác; chúng ta chỉ cần chuyển (các) bijector không bị ràng buộc của chúng ta tới hạt nhân và nó sẽ xử lý tất cả các phép biến đổi.
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
return states
precision_samples = sample()
Kiểm tra sự hội tụ
Các \(\hat{R}\) kiểm tra tụ vẻ tốt!
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013582 1.0019467] [1.0019467 1.0011805]]
So sánh với hậu quả phân tích
Một lần nữa, hãy kiểm tra lại phần sau phân tích.
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96687526 -1.6552585 ] [-1.6552585 3.867676 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329624 0.24913791] [0.24913791 0.53983927]]
Tối ưu hóa
Bây giờ chúng ta đã có mọi thứ chạy từ đầu đến cuối, hãy làm một phiên bản được tối ưu hóa hơn. Tốc độ không quan trọng quá nhiều đối với ví dụ này, nhưng một khi ma trận lớn hơn, một vài tối ưu hóa sẽ tạo ra sự khác biệt lớn.
Một cải tiến tốc độ lớn mà chúng tôi có thể thực hiện là kiểm tra lại sự phân hủy Cholesky. Lý do là hàm khả năng dữ liệu của chúng tôi yêu cầu cả hiệp phương sai và ma trận chính xác. Matrix đảo ngược là tốn kém (\(O(n^3)\) cho một \(n \times n\) ma trận), và nếu chúng ta parameterize về một trong hai hiệp phương sai hoặc ma trận chính xác, chúng ta cần phải làm một đảo ngược để có được những khác.
Như một lời nhắc nhở, một thực tế, tích cực-rõ ràng, đối xứng ma trận \(M\) có thể được chia ra thành một sản phẩm có dạng \(M = L L^T\) nơi ma trận \(L\) là tam giác thấp hơn và có đường chéo dương tính. Căn cứ vào sự phân hủy Cholesky của \(M\), chúng tôi hiệu quả hơn có thể có được cả hai \(M\) (sản phẩm của một thấp hơn và một ma trận tam giác phía trên) và \(M^{-1}\) (thông qua back-thay). Bản thân thừa số Cholesky không rẻ để tính toán, nhưng nếu chúng ta tham số hóa theo thừa số Cholesky, chúng ta chỉ cần tính toán thừa số Choleksy của các giá trị tham số ban đầu.
Sử dụng phép phân hủy Cholesky của ma trận hiệp phương sai
TFP có một phiên bản của phân phối chuẩn nhiều chiều, MultivariateNormalTriL , đó là tham số về các yếu tố Cholesky của ma trận hiệp phương sai. Vì vậy, nếu chúng ta tham số hóa theo nhân tố Cholesky của ma trận hiệp phương sai, chúng ta có thể tính toán khả năng nhật ký dữ liệu một cách hiệu quả. Thách thức là tính toán khả năng xảy ra nhật ký trước với hiệu quả tương tự.
Nếu chúng ta có một phiên bản của phân phối Wishart nghịch đảo hoạt động với các thừa số Cholesky của các mẫu, thì chúng ta đã sẵn sàng. Than ôi, chúng tôi không. (Tuy nhiên, nhóm sẽ hoan nghênh việc gửi mã!) Để thay thế, chúng tôi có thể sử dụng phiên bản phân phối Wishart hoạt động với các yếu tố Cholesky của mẫu cùng với một chuỗi bijector.
Hiện tại, chúng tôi đang thiếu một số bijector có sẵn để làm cho mọi thứ thực sự hiệu quả, nhưng tôi muốn cho thấy quá trình này như một bài tập và một minh họa hữu ích về sức mạnh của các bijector của TFP.
Phân phối Wishart hoạt động dựa trên các yếu tố Cholesky
Các Wishart phân phối có một lá cờ hữu ích, input_output_cholesky , mà quy định cụ thể rằng các ma trận đầu vào và đầu ra nên yếu tố Cholesky. Sẽ hiệu quả hơn và thuận lợi hơn về mặt số học khi làm việc với các thừa số Cholesky hơn là các ma trận đầy đủ, đó là lý do tại sao điều này là mong muốn. Một điểm quan trọng về ngữ nghĩa của lá cờ: nó chỉ có một dấu hiệu cho thấy các đại diện của các đầu vào và đầu ra để phân phối nên thay đổi - nó không chỉ ra một reparameterization đầy đủ của phân phối, trong đó sẽ bao gồm một sự điều chỉnh Jacobian đến log_prob() chức năng. Chúng tôi thực sự muốn thực hiện việc phân loại lại toàn bộ này, vì vậy chúng tôi sẽ xây dựng bản phân phối của riêng mình.
# An optimized Wishart distribution that has been transformed to operate on
# Cholesky factors instead of full matrices. Note that we gain a modest
# additional speedup by specifying the Cholesky factor of the scale matrix
# (i.e. by passing in the scale_tril parameter instead of scale).
class CholeskyWishart(tfd.TransformedDistribution):
"""Wishart distribution reparameterized to use Cholesky factors."""
def __init__(self,
df,
scale_tril,
validate_args=False,
allow_nan_stats=True,
name='CholeskyWishart'):
# Wishart has a bunch of methods that we want to support but not
# implement. We'll subclass TransformedDistribution here to take care of
# those. We'll override the few for which speed is critical and implement
# them with a separate Wishart for which input_output_cholesky=True
super(CholeskyWishart, self).__init__(
distribution=tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=False,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()),
validate_args=validate_args,
name=name
)
# Here's the Cholesky distribution we'll use for log_prob() and sample()
self.cholesky = tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=True,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats)
def _log_prob(self, x):
return (self.cholesky.log_prob(x) +
self.bijector.inverse_log_det_jacobian(x, event_ndims=2))
def _sample_n(self, n, seed=None):
return self.cholesky._sample_n(n, seed)
# some checks
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
@tf.function(autograph=False)
def compute_log_prob(m):
w_transformed = tfd.TransformedDistribution(
tfd.WishartTriL(df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()))
w_optimized = CholeskyWishart(
df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY)
log_prob_transformed = w_transformed.log_prob(m)
log_prob_optimized = w_optimized.log_prob(m)
return log_prob_transformed, log_prob_optimized
for matrix in [np.eye(2, dtype=np.float32),
np.array([[1., 0.], [2., 8.]], dtype=np.float32)]:
log_prob_transformed, log_prob_optimized = [
t.numpy() for t in compute_log_prob(matrix)]
print('Transformed Wishart:', log_prob_transformed)
print('Optimized Wishart', log_prob_optimized)
Transformed Wishart: -0.84889317 Optimized Wishart -0.84889317 Transformed Wishart: -99.269455 Optimized Wishart -99.269455
Xây dựng phân phối Wishart nghịch đảo
Chúng tôi có hiệp phương sai ma trận của chúng tôi \(C\) phân tách ra thành \(C = L L^T\) nơi \(L\) là tam giác thấp hơn và có một đường chéo dương tính. Chúng tôi muốn biết xác suất \(L\) cho rằng \(C \sim W^{-1}(\nu, V)\) nơi \(W^{-1}\) là nghịch đảo phân phối Wishart.
Sự phân bố Wishart nghịch đảo có thuộc tính rằng nếu \(C \sim W^{-1}(\nu, V)\), sau đó ma trận chính xác \(C^{-1} \sim W(\nu, V^{-1})\). Vì vậy, chúng ta có thể có được khả năng \(L\) qua một TransformedDistribution mà mất như các thông số phân phối Wishart và bijector rằng bản đồ các yếu tố Cholesky của ma trận độ chính xác đến một yếu tố Cholesky của nghịch đảo của nó.
Một cách đơn giản (nhưng không phải là siêu hiệu quả) để có được từ các yếu tố Cholesky của \(C^{-1}\) để \(L\) là để đảo ngược yếu tố Cholesky bằng trở lại giải quyết, sau đó tạo thành ma trận hiệp phương sai từ những yếu tố này đảo ngược, và sau đó làm một thừa số Cholesky .
Hãy để quá trình phân hủy Cholesky của \(C^{-1} = M M^T\). \(M\) là tam giác thấp hơn, vì vậy chúng tôi có thể nghịch nó bằng cách sử dụng MatrixInverseTriL bijector.
Hình thành \(C\) từ \(M^{-1}\) là một chút khó khăn: \(C = (M M^T)^{-1} = M^{-T}M^{-1} = M^{-T} (M^{-T})^T\). \(M\) là tam giác thấp hơn, vì vậy \(M^{-1}\) cũng sẽ có hình tam giác thấp hơn, và \(M^{-T}\) sẽ thượng tam giác. Các CholeskyOuterProduct() bijector chỉ làm việc với ma trận tam giác thấp hơn, vì vậy chúng tôi không thể sử dụng nó để tạo thành \(C\) từ \(M^{-T}\). Cách giải quyết của chúng tôi là một chuỗi bijector hoán vị các hàng và cột của ma trận.
May mắn logic này được đóng gói trong CholeskyToInvCholesky bijector!
Kết hợp tất cả các mảnh
# verify that the bijector works
m = np.array([[1., 0.], [2., 8.]], dtype=np.float32)
c_inv = m.dot(m.T)
c = np.linalg.inv(c_inv)
c_chol = np.linalg.cholesky(c)
wishart_cholesky_to_iw_cholesky = tfb.CholeskyToInvCholesky()
w_fwd = wishart_cholesky_to_iw_cholesky.forward(m).numpy()
print('numpy =\n', c_chol)
print('bijector =\n', w_fwd)
numpy = [[ 1.0307764 0. ] [-0.03031695 0.12126781]] bijector = [[ 1.0307764 0. ] [-0.03031695 0.12126781]]
Bản phân phối cuối cùng của chúng tôi
Wishart nghịch đảo của chúng tôi hoạt động dựa trên các yếu tố Cholesky như sau:
inverse_wishart_cholesky = tfd.TransformedDistribution(
distribution=CholeskyWishart(
df=PRIOR_DF,
scale_tril=np.linalg.cholesky(np.linalg.inv(PRIOR_SCALE))),
bijector=tfb.CholeskyToInvCholesky())
Chúng tôi đã có Wishart nghịch đảo của mình, nhưng nó hơi chậm vì chúng tôi phải thực hiện phân hủy Cholesky trong bijector. Hãy quay lại tham số hóa ma trận chính xác và xem chúng ta có thể làm gì ở đó để tối ưu hóa.
Phiên bản cuối cùng (!): Sử dụng phân rã Cholesky của ma trận chính xác
Một cách tiếp cận khác là làm việc với các yếu tố Cholesky của ma trận chính xác. Ở đây, hàm khả năng trước rất dễ tính toán, nhưng hàm khả năng nhật ký dữ liệu tốn nhiều công hơn vì TFP không có phiên bản của chuẩn đa biến được tham số hóa bằng độ chính xác.
Khả năng nhật ký trước được tối ưu hóa
Chúng tôi sử dụng CholeskyWishart phân phối chúng tôi xây dựng ở trên để xây dựng trước.
# Our new prior.
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
def log_lik_prior_cholesky(precisions_cholesky):
rv_precision = CholeskyWishart(
df=PRIOR_DF,
scale_tril=PRIOR_SCALE_CHOLESKY,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions_cholesky)
# Check against the slower TF implementation and the NumPy implementation.
# Note that when comparing to NumPy, we need to add in the Jacobian correction.
precisions = [np.eye(2, dtype=np.float32),
true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
lik_tf = log_lik_prior_cholesky(precisions_cholesky).numpy()
lik_tf_slow = tfd.TransformedDistribution(
distribution=tfd.WishartTriL(
df=PRIOR_DF, scale_tril=tf.linalg.cholesky(PRIOR_SCALE)),
bijector=tfb.Invert(tfb.CholeskyOuterProduct())).log_prob(
precisions_cholesky).numpy()
corrections = tfb.Invert(tfb.CholeskyOuterProduct()).inverse_log_det_jacobian(
precisions_cholesky, event_ndims=2).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow slow:', lik_tf_slow[i])
print('tensorflow fast:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow slow: -0.84889317 tensorflow fast: -0.84889317 1 numpy: -7.442875031036973 tensorflow slow: -7.442877 tensorflow fast: -7.442876
Khả năng ghi nhật ký dữ liệu được tối ưu hóa
Chúng ta có thể sử dụng bijector của TFP để xây dựng phiên bản chuẩn đa biến của riêng mình. Đây là ý tưởng chính:
Suppose I have a column vector \(X\) whose elements are iid samples of \(N(0, 1)\). We have \(\text{mean}(X) = 0\) and \(\text{cov}(X) = I\)
Now let \(Y = A X + b\). We have \(\text{mean}(Y) = b\) and \(\text{cov}(Y) = A A^T\)
Hence we can make vectors with mean \(b\) and covariance \(C\) using the affine transform \(Ax+b\) to vectors of iid standard Normal samples provided \(A A^T = C\). The Cholesky decomposition of \(C\) has the desired property. However, there are other solutions.
Let \(P = C^{-1}\) and let the Cholesky decomposition of \(P\) be \(B\), ie \(B B^T = P\). Now
\(P^{-1} = (B B^T)^{-1} = B^{-T} B^{-1} = B^{-T} (B^{-T})^T\)
So another way to get our desired mean and covariance is to use the affine transform \(Y=B^{-T}X + b\).
Our approach (courtesy of this notebook ):
- Use
tfd.Independent()to combine a batch of 1-DNormalrandom variables into a single multi-dimensional random variable. Thereinterpreted_batch_ndimsparameter forIndependent()specifies the number of batch dimensions that should be reinterpreted as event dimensions. In our case we create a 1-D batch of length 2 that we transform into a 1-D event of length 2, soreinterpreted_batch_ndims=1. - Apply a bijector to add the desired covariance:
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky, adjoint=True)). Note that above we're multiplying our iid normal random variables by the transpose of the inverse of the Cholesky factor of the precision matrix \((B^{-T}X)\). Thetfb.Inverttakes care of inverting \(B\), and theadjoint=Trueflag performs the transpose. - Apply a bijector to add the desired offset:
tfb.Shift(shift=shift)Note that we have to do the shift as a separate step from the initial inverted affine transform because otherwise the inverted scale is applied to the shift (since the inverse of \(y=Ax+b\) is \(x=A^{-1}y - A^{-1}b\)).
class MVNPrecisionCholesky(tfd.TransformedDistribution):
"""Multivariate normal parameterized by loc and Cholesky precision matrix."""
def __init__(self, loc, precision_cholesky, name=None):
super(MVNPrecisionCholesky, self).__init__(
distribution=tfd.Independent(
tfd.Normal(loc=tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky,
adjoint=True)),
]),
name=name)
@tf.function(autograph=False)
def log_lik_data_cholesky(precisions_cholesky, replicated_data):
n = tf.shape(precisions_cholesky)[0] # number of precision matrices
rv_data = MVNPrecisionCholesky(
loc=tf.zeros([n, 2]),
precision_cholesky=precisions_cholesky)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# check against the numpy implementation
true_precision_cholesky = np.linalg.cholesky(true_precision)
precisions = [np.eye(2, dtype=np.float32), true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
n = precisions_cholesky.shape[0]
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
lik_tf = log_lik_data_cholesky(precisions_cholesky, replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.81824
Combined log likelihood function
Now we combine our prior and data log likelihood functions in a closure.
def get_log_lik_cholesky(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_cholesky(precisions_cholesky):
return (log_lik_data_cholesky(precisions_cholesky, replicated_data) +
log_lik_prior_cholesky(precisions_cholesky))
return _log_lik_cholesky
Constraining bijector
Our samples are constrained to be valid Cholesky factors, which means they must be lower triangular matrices with positive diagonals. The TransformedTransitionKernel needs a bijector that maps unconstrained tensors to/from tensors with our desired constraints. We've removed the Cholesky decomposition from the bijector's inverse, which speeds things up.
unconstrained_to_precision_cholesky = tfb.Chain([
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: expand the vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# some checks
inv = unconstrained_to_precision_cholesky.inverse(precisions_cholesky).numpy()
fwd = unconstrained_to_precision_cholesky.forward(inv).numpy()
print('precisions_cholesky:\n', precisions_cholesky)
print('\ninv:\n', inv)
print('\nfwd(inv):\n', fwd)
precisions_cholesky: [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]] inv: [[ 0.0000000e+00 0.0000000e+00 0.0000000e+00] [ 3.5762781e-07 -2.0647411e+00 1.3721828e-01]] fwd(inv): [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]]
Initial values
We generate a tensor of initial values. We're working with Cholesky factors, so we generate some Cholesky factor initial values.
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values_cholesky = []
for i in range(N_CHAINS):
initial_values_cholesky.append(np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32))
initial_values_cholesky = np.stack(initial_values_cholesky)
Sampling
We sample N_CHAINS chains using the TransformedTransitionKernel .
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_cholesky(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision_cholesky)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
samples = tf.linalg.matmul(states, states, transpose_b=True)
return samples
precision_samples = sample()
Convergence check
A quick convergence check looks good:
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013583 1.0019467] [1.0019467 1.0011804]]
Comparing results to the analytic posterior
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, newshape=[-1, 2, 2])
And again, the sample means and standard deviations match those of the analytic posterior.
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.9668749 -1.6552604] [-1.6552604 3.8676758]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329637 0.24913797] [0.24913797 0.53983945]]
Ok, all done! We've got our optimized sampler working.
