Zobacz na TensorFlow.org

Uruchom w Google Colab

Wyświetl źródło na GitHub

Pobierz notatnik

Napisałem ten notatnik jako studium przypadku, aby poznać prawdopodobieństwo TensorFlow. Problem, który wybrałem do rozwiązania, to oszacowanie macierzy kowariancji dla próbek 2-D średniej 0 zmiennej losowej Gaussa. Problem ma kilka fajnych funkcji:

• Jeśli użyjemy odwrotnego Wisharta przed dla kowariancji (powszechne podejście), problem ma rozwiązanie analityczne, więc możemy sprawdzić nasze wyniki.
• Problem polega na próbkowaniu ograniczonego parametru, co dodaje interesującej złożoności.
• Najprostsze rozwiązanie nie jest najszybsze, więc należy wykonać pewne prace optymalizacyjne.

Postanowiłem spisywać moje doświadczenia w miarę postępów. Zajęło mi trochę czasu, aby zastanowić się nad niuansami TFP, więc ten notebook zaczyna się dość prosto, a następnie stopniowo przechodzi do bardziej skomplikowanych funkcji TFP. Po drodze napotkałem wiele problemów i próbowałem uchwycić zarówno procesy, które pomogły mi je zidentyfikować, jak i rozwiązania, które w końcu znalazłem. Starałem się zawierać wiele szczegółów (w tym wiele badań, aby upewnić się poszczególne etapy są poprawne).

Dlaczego warto uczyć się prawdopodobieństwa TensorFlow?

Uznałem, że TensorFlow Probability jest atrakcyjny dla mojego projektu z kilku powodów:

• Prawdopodobieństwo TensorFlow umożliwia interaktywne tworzenie prototypów złożonych modeli w notatniku. Możesz podzielić swój kod na małe fragmenty, które możesz testować interaktywnie i za pomocą testów jednostkowych.
• Gdy będziesz gotowy do skalowania, możesz skorzystać z całej infrastruktury, którą mamy, aby TensorFlow działał na wielu zoptymalizowanych procesorach na wielu komputerach.
• Wreszcie, chociaż naprawdę lubię Stana, trudno mi go debugować. Musisz napisać cały swój kod modelowania w samodzielnym języku, który ma bardzo niewiele narzędzi pozwalających na grzebanie w kodzie, sprawdzanie stanów pośrednich i tak dalej.

Minusem jest to, że TensorFlow Probability jest znacznie nowszy niż Stan i PyMC3, więc dokumentacja jest w toku, a wiele funkcji nie zostało jeszcze zbudowane. Na szczęście stwierdziłem, że podstawa TFP jest solidna i została zaprojektowana w sposób modułowy, co pozwala w dość prosty sposób rozszerzyć jego funkcjonalność. W tym zeszycie, oprócz rozwiązania studium przypadku, pokażę kilka sposobów na rozszerzenie TFP.

Dla kogo to jest?

Zakładam, że czytelnicy przychodzą do tego notatnika z kilkoma ważnymi warunkami wstępnymi. Powinieneś:

• Znajomość podstaw wnioskowania bayesowskiego. (Jeśli nie, to naprawdę miłe pierwsza książka jest Rethinking statystyczne )
• Masz jakieś znajomości biblioteki próbkowania MCMC, np STAN / PyMC3 / BŁĘDY
• Mieć solidne zrozumienie NumPy (Jeden dobry intro jest Python do analizy danych )
• Mieć co najmniej mijania znajomości TensorFlow , ale niekoniecznie ekspertyzy. ( Learning TensorFlow jest dobra, ale TensorFlow Rapid środki evolution że większość książek będzie nieco przestarzałe. Stanford CS20 Oczywiście jest również dobre).

Pierwsze podejscie

Oto moja pierwsza próba rozwiązania problemu. Spoiler: moje rozwiązanie nie działa i trzeba będzie kilku prób, aby wszystko naprawić! Chociaż proces ten zajmuje trochę czasu, każda z poniższych prób była przydatna do nauki nowej części TFP.

Jedna uwaga: TFP nie implementuje obecnie odwróconej dystrybucji Wishart (na końcu zobaczymy, jak rzucić nasz własny odwrotny Wishart), więc zamiast tego zmienię problem na szacowanie precyzyjnej macierzy przy użyciu wcześniejszego Wisharta.

import collections
import math
import os
import time

import numpy as np
import pandas as pd
import scipy
import scipy.stats
import matplotlib.pyplot as plt

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors

Krok 1: zbierz obserwacje razem

Moje dane tutaj są syntetyczne, więc będzie to wyglądało na nieco bardziej uporządkowane niż przykład ze świata rzeczywistego. Nie ma jednak powodu, dla którego nie możesz samodzielnie wygenerować niektórych syntetycznych danych.

Wskazówka: Po wybraniu w postaci modelu, można wybrać kilka wartości parametrów i korzystać z wybranego modelu, aby wygenerować pewne dane syntetyczne. W ramach kontroli poprawności implementacji możesz zweryfikować, czy szacunki zawierają prawdziwe wartości wybranych parametrów. Aby przyspieszyć cykl debugowania/testowania, możesz rozważyć uproszczoną wersję swojego modelu (np. użyj mniejszej liczby wymiarów lub mniejszej liczby próbek).

Wskazówka: To najłatwiejszy do pracy ze swoimi obserwacjami jak macierze numpy. Należy zauważyć, że NumPy domyślnie używa float64, podczas gdy TensorFlow domyślnie używa float32.

Ogólnie rzecz biorąc, operacje TensorFlow wymagają, aby wszystkie argumenty miały ten sam typ i musisz wykonać jawne rzutowanie danych, aby zmienić typy. Jeśli używasz obserwacji float64, będziesz musiał dodać wiele operacji rzutowania. Natomiast NumPy zajmie się rzucaniem automatycznie. Stąd, jest o wiele łatwiejsze do konwertowania danych NumPy do float32 niż jest zmusić TensorFlow do użytku float64.

Wybierz kilka wartości parametrów

# We're assuming 2-D data with a known true mean of (0, 0)
true_mean = np.zeros([2], dtype=np.float32)
# We'll make the 2 coordinates correlated
true_cor = np.array([[1.0, 0.9], [0.9, 1.0]], dtype=np.float32)
# And we'll give the 2 coordinates different variances
true_var = np.array([4.0, 1.0], dtype=np.float32)
# Combine the variances and correlations into a covariance matrix
true_cov = np.expand_dims(np.sqrt(true_var), axis=1).dot(
    np.expand_dims(np.sqrt(true_var), axis=1).T) * true_cor
# We'll be working with precision matrices, so we'll go ahead and compute the
# true precision matrix here
true_precision = np.linalg.inv(true_cov)

# Here's our resulting covariance matrix
print(true_cov)
# Verify that it's positive definite, since np.random.multivariate_normal
# complains about it not being positive definite for some reason.
# (Note that I'll be including a lot of sanity checking code in this notebook -
# it's a *huge* help for debugging)
print('eigenvalues: ', np.linalg.eigvals(true_cov))

[[4.  1.8]
 [1.8 1. ]]
eigenvalues:  [4.843075   0.15692513]

Wygeneruj syntetyczne obserwacje

Zauważ, że TensorFlow Prawdopodobieństwo wykorzystuje konwencję, że początkowy wymiar (y) danych reprezentują przykładowe wskaźniki, a ostateczny wymiar (y) danych reprezentują wymiarowości swoich próbek.

Tutaj chcemy 100 próbek, z których każda jest wektorem o długości 2. Będziemy wygenerować tablicę my_data z kształtu (100, 2). my_data[i, :] jest \(i\)próbka i jest wektor o długości 2.

(Pamiętaj, aby my_data mieć typ float32!)

# Set the seed so the results are reproducible.
np.random.seed(123)

# Now generate some observations of our random variable.
# (Note that I'm suppressing a bunch of spurious about the covariance matrix
# not being positive semidefinite via check_valid='ignore' because it really is
# positive definite!)
my_data = np.random.multivariate_normal(
    mean=true_mean, cov=true_cov, size=100,
    check_valid='ignore').astype(np.float32)

my_data.shape

(100, 2)

Poczytalność sprawdź obserwacje

Jednym z potencjalnych źródeł błędów jest zepsucie danych syntetycznych! Zróbmy kilka prostych sprawdzeń.

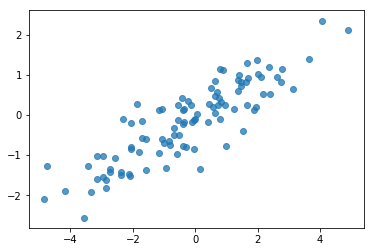
# Do a scatter plot of the observations to make sure they look like what we
# expect (higher variance on the x-axis, y values strongly correlated with x)
plt.scatter(my_data[:, 0], my_data[:, 1], alpha=0.75)
plt.show()

print('mean of observations:', np.mean(my_data, axis=0))
print('true mean:', true_mean)

mean of observations: [-0.24009615 -0.16638893]
true mean: [0. 0.]

print('covariance of observations:\n', np.cov(my_data, rowvar=False))
print('true covariance:\n', true_cov)

covariance of observations:
 [[3.95307734 1.68718486]
 [1.68718486 0.94910269]]
true covariance:
 [[4.  1.8]
 [1.8 1. ]]

Ok, nasze próbki wyglądają rozsądnie. Następny krok.

Krok 2: Zaimplementuj funkcję wiarygodności w NumPy

Najważniejszą rzeczą, którą będziemy musieli napisać, aby wykonać nasze próbkowanie MCMC w TF Probability, jest funkcja logarytmiczna wiarygodności. Ogólnie rzecz biorąc, pisanie TF jest nieco trudniejsze niż NumPy, więc uważam, że pomocne jest wykonanie początkowej implementacji w NumPy. Mam zamiar podzielić funkcję wiarogodności na 2 części, funkcja wiarygodności danych, który odpowiada \(P(data | parameters)\) i wcześniejszej funkcji prawdopodobieństwa, który odpowiada \(P(parameters)\).

Zauważ, że te funkcje NumPy nie muszą być super zoptymalizowane / zwektoryzowane, ponieważ celem jest po prostu wygenerowanie pewnych wartości do testowania. Kluczową kwestią jest poprawność!

Najpierw zaimplementujemy element wiarygodności dziennika danych. To całkiem proste. Jedyną rzeczą do zapamiętania jest to, że będziemy pracować z macierzami precyzyjnymi, więc odpowiednio sparametryzujemy.

def log_lik_data_numpy(precision, data):
  # np.linalg.inv is a really inefficient way to get the covariance matrix, but
  # remember we don't care about speed here
  cov = np.linalg.inv(precision)
  rv = scipy.stats.multivariate_normal(true_mean, cov)
  return np.sum(rv.logpdf(data))

# test case: compute the log likelihood of the data given the true parameters
log_lik_data_numpy(true_precision, my_data)

-280.81822950593767

Mamy zamiar użyć Wishart przed dla matrycy precyzji ponieważ istnieje analityczne rozwiązanie dla tylnej (patrz poręczny stolik Wikipedii koniugatu priors ).

Rozkład Wishart ma 2 parametry:

• liczba stopni swobody (oznaczony \(\nu\) w Wikipedii)
• macierz skala (oznaczony \(V\) w Wikipedia)

Średnią dla dystrybucji Wishart z parametrami \(\nu, V\) jest \(E[W] = \nu V\), a wariancja jest \(\text{Var}(W_{ij}) = \nu(v_{ij}^2+v_{ii}v_{jj})\)

Niektóre użyteczne intuicja: Można wygenerować próbkę Wishart generując \(\nu\) niezależnie rysuje \(x_1 \ldots x_{\nu}\) z wielowymiarowej zmiennej losowej normalnej ze średnią 0 i kowariancji \(V\) a następnie tworząc sumę \(W = \sum_{i=1}^{\nu} x_i x_i^T\).

Jeśli przeskalować próbek Wishart przez podzielenie ich przez \(\nu\), masz przykładową macierz kowariancji \(x_i\). Próbka ta macierz kowariancji powinien zbliżać w kierunku \(V\) jako \(\nu\) wzrasta. Gdy \(\nu\) jest mała, jest wiele różnic w przykładowej macierzy kowariancji tak małe wartości \(\nu\) odpowiadają słabszych priors i duże wartości \(\nu\) odpowiadają silniejszych priors. Zauważ, że \(\nu\) musi być co najmniej tak duży jak wymiar przestrzeni jesteś próbkowania lub będziesz wygenerowania pojedynczej macierzy.

Użyjemy \(\nu = 3\) więc mamy słaby przed i weźmiemy \(V = \frac{1}{\nu} I\) która będzie ciągnąć naszą prognozę kowariancji ku tożsamości (Przypomnijmy, że średnia jest \(\nu V\)).

PRIOR_DF = 3
PRIOR_SCALE = np.eye(2, dtype=np.float32) / PRIOR_DF

def log_lik_prior_numpy(precision):
  rv = scipy.stats.wishart(df=PRIOR_DF, scale=PRIOR_SCALE)
  return rv.logpdf(precision)

# test case: compute the prior for the true parameters
log_lik_prior_numpy(true_precision)

-9.103606346649766

Rozkład Wishart jest koniugat przed szacowania macierzy precyzją wielowymiarowa normalne w znanej średniej \(\mu\).

Załóżmy, że wcześniejsze parametry Wishart są \(\nu, V\) i że mamy \(n\) obserwacje naszej wielowymiarowej normalnej \(x_1, \ldots, x_n\). Tylnej parametry \(n + \nu, \left(V^{-1} + \sum_{i=1}^n (x_i-\mu)(x_i-\mu)^T \right)^{-1}\).

n = my_data.shape[0]
nu_prior = PRIOR_DF
v_prior = PRIOR_SCALE
nu_posterior = nu_prior + n
v_posterior = np.linalg.inv(np.linalg.inv(v_prior) + my_data.T.dot(my_data))
posterior_mean = nu_posterior * v_posterior
v_post_diag = np.expand_dims(np.diag(v_posterior), axis=1)
posterior_sd = np.sqrt(nu_posterior *
                       (v_posterior ** 2.0 + v_post_diag.dot(v_post_diag.T)))

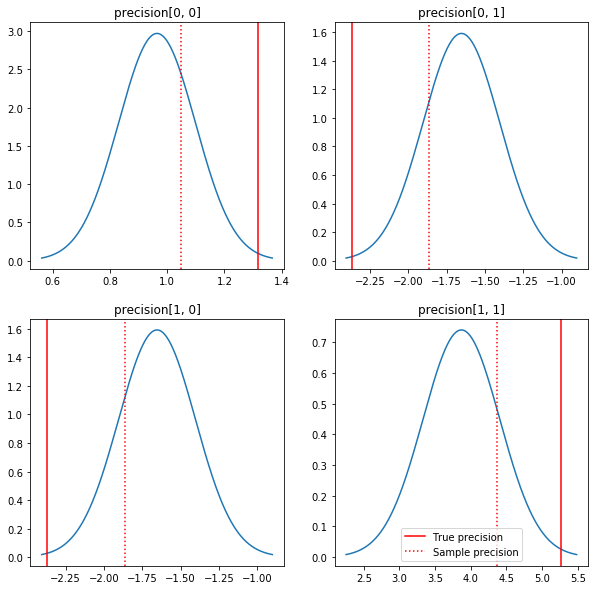
Szybki wykres tylnych i prawdziwych wartości. Zauważ, że tyły są blisko tyłów próbki, ale są nieco skurczone w kierunku tożsamości. Zauważ też, że prawdziwe wartości są dość dalekie od trybu a posteriori — przypuszczalnie dzieje się tak dlatego, że przed nie jest zbyt dobrym dopasowaniem do naszych danych. W prawdziwym problemem my prawdopodobnie lepiej z czymś skalowany przed odwrotną Wishart dla kowariancji (patrz, na przykład, Andrew Gelman za komentarz na ten temat), ale wtedy nie mielibyśmy piękny analityczną tylnej.

sample_precision = np.linalg.inv(np.cov(my_data, rowvar=False, bias=False))
fig, axes = plt.subplots(2, 2)
fig.set_size_inches(10, 10)
for i in range(2):
  for j in range(2):
    ax = axes[i, j]
    loc = posterior_mean[i, j]
    scale = posterior_sd[i, j]
    xmin = loc - 3.0 * scale
    xmax = loc + 3.0 * scale
    x = np.linspace(xmin, xmax, 1000)
    y = scipy.stats.norm.pdf(x, loc=loc, scale=scale)
    ax.plot(x, y)
    ax.axvline(true_precision[i, j], color='red', label='True precision')
    ax.axvline(sample_precision[i, j], color='red', linestyle=':', label='Sample precision')
    ax.set_title('precision[%d, %d]' % (i, j))
plt.legend()
plt.show()

Krok 3: Zaimplementuj funkcję wiarygodności w TensorFlow

Spoiler: Nasza pierwsza próba nie zadziała; porozmawiamy o tym poniżej.

Wskazówka: Użyj TensorFlow tryb chętny przy opracowywaniu swoich funkcji wiarogodności. Tryb chętny sprawia TF zachowują się jak NumPy - wszystko uruchamiany zaraz, więc można debugować interaktywnie zamiast używać Session.run() . Zobacz nuty tutaj .

Wstępne: Klasy dystrybucji

TFP posiada kolekcję klas dystrybucji, których użyjemy do wygenerowania naszych prawdopodobieństw logów. Należy zauważyć, że te klasy działają z tensorami próbek, a nie tylko z pojedynczymi próbkami - pozwala to na wektoryzację i związane z tym przyspieszenie.

Dystrybucja może działać z tensorem próbek na 2 różne sposoby. Najprościej jest zilustrować te 2 sposoby konkretnym przykładem obejmującym dystrybucję z pojedynczym parametrem skalarnym. Użyję Poissona rozkładu, która ma rate parametr.

• Jeśli stworzymy Poissona z pojedynczej wartości dla rate parametru, wywołanie jej sample() metody zwracają pojedynczą wartość. Wartość ta nazywa się event , w tym przypadku zdarzenia są wszystkie skalary.
• Jeśli stworzymy Poissona z tensora wartości dla rate parametru, wezwanie do jego sample() metoda zwraca obecnie wiele wartości, po jednym dla każdej wartości tensora stopy. Przedmiotem działa jako zbiór niezależnych Poissons, każdy z inną prędkością, a każda z wartości zwracane przez wywołanie sample() odpowiada jednemu z tych Poissons. Ten zbiór niezależnych, ale nie identycznie rozproszonych wydarzeń nazywa się batch .
• sample() Sposób wykonuje sample_shape parametru, który domyślnie pustej krotki. Przechodząc niepusty wartość dla sample_shape wyniki w próbie powracających kilku partiach. Ten zbiór partii nazywany jest sample .

Dystrybucja za log_prob() metoda pobiera dane w taki sposób, że podobieństw jak sample() generuje go. log_prob() zwraca prawdopodobieństwa dla próbek, czyli dla wielu, niezależnych partii zdarzeń.

• Jeśli mamy obiekt Poissona, który został utworzony z skalarnym rate , każda partia jest skalarne, a jeśli mijamy w tensora próbek, będziemy wysiadać tensora tej samej wielkości prawdopodobieństw dziennika.
• Jeśli mamy obiekt Poissona, który został utworzony z tensora kształtu T od rate wartości, każda partia jest tensor kształcie T . Jeśli przejdziemy przez tensor próbek o kształcie D, T, otrzymamy tensor logarytmicznych prawdopodobieństw o ​​kształcie D, T.

Poniżej kilka przykładów ilustrujących te przypadki. Zobacz ten notatnik na bardziej szczegółowy poradnik na temat wydarzeń, partii i kształtów.

# case 1: get log probabilities for a vector of iid draws from a single
# normal distribution
norm1 = tfd.Normal(loc=0., scale=1.)
probs1 = norm1.log_prob(tf.constant([1., 0.5, 0.]))

# case 2: get log probabilities for a vector of independent draws from
# multiple normal distributions with different parameters.  Note the vector
# values for loc and scale in the Normal constructor.
norm2 = tfd.Normal(loc=[0., 2., 4.], scale=[1., 1., 1.])
probs2 = norm2.log_prob(tf.constant([1., 0.5, 0.]))

print('iid draws from a single normal:', probs1.numpy())
print('draws from a batch of normals:', probs2.numpy())

iid draws from a single normal: [-1.4189385 -1.0439385 -0.9189385]
draws from a batch of normals: [-1.4189385 -2.0439386 -8.918939 ]

Prawdopodobieństwo dziennika danych

Najpierw zaimplementujemy funkcję wiarygodności dziennika danych.

VALIDATE_ARGS = True
ALLOW_NAN_STATS = False

Jedną z kluczowych różnic w porównaniu z przypadkiem NumPy jest to, że nasza funkcja prawdopodobieństwa TensorFlow będzie musiała obsługiwać wektory precyzyjnych macierzy, a nie tylko pojedyncze macierze. Wektory parametrów zostaną użyte podczas próbkowania z wielu łańcuchów.

Stworzymy obiekt dystrybucji, który będzie działał z serią precyzyjnych macierzy (tj. jedna macierz na łańcuch).

Podczas obliczania prawdopodobieństw dziennika naszych danych będziemy potrzebować replikacji naszych danych w taki sam sposób, jak nasze parametry, tak aby jedna kopia przypadała na zmienną wsadową. Kształt naszych replikowanych danych będzie musiał wyglądać następująco:

[sample shape, batch shape, event shape]

W naszym przypadku kształt zdarzenia to 2 (ponieważ pracujemy z gaussami 2-D). Kształt próbki to 100, ponieważ mamy 100 próbek. Kształt wsadu będzie po prostu liczbą precyzyjnych macierzy, z którymi pracujemy. Replikowanie danych za każdym razem, gdy wywołujemy funkcję wiarygodności, jest marnotrawstwem, więc zreplikujemy dane z wyprzedzeniem i przekażemy je w zreplikowanej wersji.

Należy pamiętać, że jest to nieefektywne realizacja: MultivariateNormalFullCovariance jest drogie w stosunku do niektórych rozwiązań, które omówimy w rozdziale optymalizacji na końcu.

def log_lik_data(precisions, replicated_data):
  n = tf.shape(precisions)[0]  # number of precision matrices
  # We're estimating a precision matrix; we have to invert to get log
  # probabilities.  Cholesky inversion should be relatively efficient,
  # but as we'll see later, it's even better if we can avoid doing the Cholesky
  # decomposition altogether.
  precisions_cholesky = tf.linalg.cholesky(precisions)
  covariances = tf.linalg.cholesky_solve(
      precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
  rv_data = tfd.MultivariateNormalFullCovariance(
      loc=tf.zeros([n, 2]),
      covariance_matrix=covariances,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)

  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# For our test, we'll use a tensor of 2 precision matrices.
# We'll need to replicate our data for the likelihood function.
# Remember, TFP wants the data to be structured so that the sample dimensions
# are first (100 here), then the batch dimensions (2 here because we have 2
# precision matrices), then the event dimensions (2 because we have 2-D
# Gaussian data).  We'll need to add a middle dimension for the batch using
# expand_dims, and then we'll need to create 2 replicates in this new dimension
# using tile.
n = 2
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
print(replicated_data.shape)

(100, 2, 2)

Wskazówka: Jedną z rzeczy, znalazłem się być niezwykle pomocne jest pisanie małych testów poprawności moich funkcji TensorFlow. Naprawdę łatwo jest zepsuć wektoryzację w TF, więc posiadanie prostszych funkcji NumPy jest świetnym sposobem na zweryfikowanie wyjścia TF. Pomyśl o nich jak o małych testach jednostkowych.

# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_data(precisions, replicated_data=replicated_data).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.8182

Prawdopodobieństwo wcześniejszego logu

Wcześniejszy jest łatwiejszy, ponieważ nie musimy się martwić o replikację danych.

@tf.function(autograph=False)
def log_lik_prior(precisions):
  rv_precision = tfd.WishartTriL(
      df=PRIOR_DF,
      scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)
  return rv_precision.log_prob(precisions)

# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_prior(precisions).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]))
  print('tensorflow:', lik_tf[i])

0
numpy: -2.2351873809649625
tensorflow: -2.2351875
1
numpy: -9.103606346649766
tensorflow: -9.103608

Zbuduj wspólną funkcję wiarygodności logarytmicznej

Powyższa funkcja prawdopodobieństwa dziennika danych zależy od naszych obserwacji, ale próbnik nie będzie ich miał. Możemy pozbyć się zależności bez użycia zmiennej globalnej, używając [zamknięcia](https://en.wikipedia.org/wiki/Closure_(computer_programming). Zamknięcia obejmują zewnętrzną funkcję, która buduje środowisko zawierające zmienne potrzebne funkcja wewnętrzna.

def get_log_lik(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik(precision):
    return log_lik_data(precision, replicated_data) + log_lik_prior(precision)

  return _log_lik

Krok 4: Próbka

Ok, czas na spróbowanie! Aby uprościć sprawę, użyjemy po prostu 1 łańcucha i użyjemy macierzy tożsamości jako punktu wyjścia. Później zrobimy rzeczy ostrożniej.

Ponownie, to nie zadziała – dostaniemy wyjątek.

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  init_precision = tf.expand_dims(tf.eye(2), axis=0)

  # Use expand_dims because we want to pass in a tensor of starting values
  log_lik_fn = get_log_lik(my_data, n_chains=1)

  # we'll just do a few steps here
  num_results = 10
  num_burnin_steps = 10
  states = tfp.mcmc.sample_chain(
     num_results=num_results,
     num_burnin_steps=num_burnin_steps,
     current_state=[
         init_precision,
     ],
     kernel=tfp.mcmc.HamiltonianMonteCarlo(
         target_log_prob_fn=log_lik_fn,
         step_size=0.1,
         num_leapfrog_steps=3),
     trace_fn=None,
     seed=123)
  return states

try:
  states = sample()
except Exception as e:
  # shorten the giant stack trace
  lines = str(e).split('\n')
  print('\n'.join(lines[:5]+['...']+lines[-3:]))

Cholesky decomposition was not successful. The input might not be valid.
     [[{ {node mcmc_sample_chain/trace_scan/while/body/_79/smart_for_loop/while/body/_371/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_537/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/StatefulPartitionedCall/Cholesky} }]] [Op:__inference_sample_2849]

Function call stack:
sample
...
Function call stack:
sample

Identyfikacja problemu

InvalidArgumentError (see above for traceback): Cholesky decomposition was not successful. The input might not be valid. To nie jest zbyt pomocne. Zobaczmy, czy możemy dowiedzieć się więcej o tym, co się stało.

• Wydrukujemy parametry dla każdego kroku, abyśmy mogli zobaczyć wartość, dla której coś się nie powiedzie
• Dodamy kilka asercji, aby zabezpieczyć się przed konkretnymi problemami.

Asercje są trudne, ponieważ są to operacje TensorFlow i musimy uważać, aby zostały wykonane i nie zostały zoptymalizowane poza wykresem. To warto przeczytać ten przegląd z TensorFlow debugowania, jeśli nie są zaznajomieni z twierdzeniami TF. Można jawnie wymusić twierdzeń wykonać używając tf.control_dependencies (patrz komentarze w kodzie poniżej).

Rodzimy TensorFlow za Print funkcja ma takie samo zachowanie jak twierdzeń - jest to operacja, i trzeba trochę starań, aby upewnić się, że jest on wykonywany. Print powoduje dodatkowe bóle głowy, kiedy pracujemy w zeszycie: jego produkcja zostanie wysłana do stderr i stderr nie jest wyświetlana w komórce. Użyjemy trick tutaj: zamiast używać tf.Print , my tworzymy naszą własną operację drukowania TensorFlow poprzez tf.pyfunc . Podobnie jak w przypadku asercji, musimy upewnić się, że nasza metoda zostanie wykonana.

def get_log_lik_verbose(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  def _log_lik(precisions):
    # An internal method we'll make into a TensorFlow operation via tf.py_func
    def _print_precisions(precisions):
      print('precisions:\n', precisions)
      return False  # operations must return something!
    # Turn our method into a TensorFlow operation
    print_op = tf.compat.v1.py_func(_print_precisions, [precisions], tf.bool)

    # Assertions are also operations, and some care needs to be taken to ensure
    # that they're executed
    assert_op = tf.assert_equal(
        precisions, tf.linalg.matrix_transpose(precisions),
        message='not symmetrical', summarize=4, name='symmetry_check')

    # The control_dependencies statement forces its arguments to be executed
    # before subsequent operations
    with tf.control_dependencies([print_op, assert_op]):
      return (log_lik_data(precisions, replicated_data) +
              log_lik_prior(precisions))

  return _log_lik

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  init_precision = tf.eye(2)[tf.newaxis, ...]
  log_lik_fn = get_log_lik_verbose(my_data)
  # we'll just do a few steps here
  num_results = 10
  num_burnin_steps = 10
  states = tfp.mcmc.sample_chain(
      num_results=num_results,
      num_burnin_steps=num_burnin_steps,
      current_state=[
          init_precision,
      ],
      kernel=tfp.mcmc.HamiltonianMonteCarlo(
          target_log_prob_fn=log_lik_fn,
          step_size=0.1,
          num_leapfrog_steps=3),
      trace_fn=None,
      seed=123)

try:
  states = sample()
except Exception as e:
  # shorten the giant stack trace
  lines = str(e).split('\n')
  print('\n'.join(lines[:5]+['...']+lines[-3:]))

precisions:
 [[[1. 0.]
  [0. 1.]]]
precisions:
 [[[1. 0.]
  [0. 1.]]]
precisions:
 [[[ 0.24315196 -0.2761638 ]
  [-0.33882257  0.8622    ]]]
 assertion failed: [not symmetrical] [Condition x == y did not hold element-wise:] [x (leapfrog_integrate_one_step/add:0) = ] [[[0.243151963 -0.276163787][-0.338822573 0.8622]]] [y (leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/matrix_transpose/transpose:0) = ] [[[0.243151963 -0.338822573][-0.276163787 0.8622]]]
     [[{ {node mcmc_sample_chain/trace_scan/while/body/_96/smart_for_loop/while/body/_381/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_503/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/symmetry_check_1/Assert/AssertGuard/else/_577/Assert} }]] [Op:__inference_sample_4837]

Function call stack:
sample
...
Function call stack:
sample

Dlaczego to się nie udaje

Pierwszą nową wartością parametru, której próbuje próbnik, jest asymetryczna macierz. To powoduje, że rozkład Cholesky'ego nie powiedzie się, ponieważ jest zdefiniowany tylko dla symetrycznych (i dodatnio określonych) macierzy.

Problem polega na tym, że naszym parametrem będącym przedmiotem zainteresowania jest macierz precyzji, a macierze precyzji muszą być rzeczywiste, symetryczne i dodatnio określone. Próbnik nie wie nic o tym ograniczeniu (może z wyjątkiem gradientów), więc jest całkowicie możliwe, że próbnik zaproponuje nieprawidłową wartość, prowadząc do wyjątku, szczególnie jeśli rozmiar kroku jest duży.

Dzięki próbnikowi Hamiltonianu Monte Carlo możemy obejść ten problem, używając bardzo małego rozmiaru kroku, ponieważ gradient powinien utrzymywać parametry z dala od nieprawidłowych regionów, ale małe rozmiary kroku oznaczają wolną zbieżność. Z samplerem Metropolis-Hastings, który nie wie nic o gradientach, jesteśmy zgubieni.

Wersja 2: reparametryzacja do parametrów nieograniczonych

Istnieje proste rozwiązanie powyższego problemu: możemy przeparametryzować nasz model w taki sposób, aby nowe parametry nie miały już tych ograniczeń. TFP dostarcza użyteczny zestaw narzędzi - bijectors - właśnie do tego.

Reparametryzacja z bijektorami

Nasza macierz precyzji musi być rzeczywista i symetryczna; chcemy alternatywnej parametryzacji, która nie ma tych ograniczeń. Punktem wyjścia jest faktoryzacja Cholesky'ego macierzy precyzji. Czynniki Cholesky'ego są nadal ograniczone - są trójkątne dolne, a ich elementy ukośne muszą być dodatnie. Jeśli jednak weźmiemy logarytm przekątnych czynnika Cholesky'ego, logarytmy nie są już ograniczone jako dodatnie, a następnie, jeśli spłaszczymy dolną część trójkąta do wektora 1-D, nie będziemy już mieli ograniczenia trójkąta dolnego . Wynikiem w naszym przypadku będzie wektor o długości 3 bez ograniczeń.

(The obsługi Stan ma wielki rozdział za pomocą przekształceń usunąć różnego rodzaju ograniczeniami na parametry).

Ta zmiana parametrów ma niewielki wpływ na naszą funkcję wiarygodności logu danych — musimy tylko odwrócić nasze przekształcenie, aby odzyskać macierz precyzji — ale wpływ na a priori jest bardziej skomplikowany. Określiliśmy, że prawdopodobieństwo danej macierzy dokładności jest określone przez rozkład Wisharta; jakie jest prawdopodobieństwo naszej przekształconej macierzy?

Przypomnijmy, że jeśli zastosujemy funkcję monotoniczny \(g\) do 1-D zmienna losowa \(X\), \(Y = g(X)\)gęstość dla \(Y\) jest dana przez

\[ f_Y(y) = | \frac{d}{dy}(g^{-1}(y)) | f_X(g^{-1}(y)) \]

Pochodna \(g^{-1}\) perspektywie odpowiada za sposób \(g\) zmienia lokalnych woluminów. Dla wyższych wymiarów zmiennych losowych, współczynnik korygująca jest wartość bezwzględna wyznacznika Jacobiego z \(g^{-1}\) (patrz tutaj ).

Będziemy musieli dodać jakobian odwrotnej transformacji do naszej logarytmicznej funkcji a priori wiarygodności. Szczęśliwie, TFP jest Bijector klasa może zająć się tym za nas.

Bijector klasa jest używana do reprezentowania odwracalne, gładkie funkcje służące do zmiany zmiennych w funkcji gęstości prawdopodobieństwa. Bijectors wszyscy mają forward() metodę, która wykonuje przekształcenie, to inverse() metodę, która odwraca go i forward_log_det_jacobian() i inverse_log_det_jacobian() metody, które dostarczają jakobian korekt musimy kiedy reparaterize pdf.

TFP stanowi zbiór przydatnych bijectors które można łączyć z kompozycją za pośrednictwem Chain operatora w celu wytworzenia bardzo skomplikowanych transformacji. W naszym przypadku skomponujemy następujące 3 bijektory (operacje w łańcuchu wykonujemy od prawej do lewej):

1. Pierwszym krokiem naszej transformacji jest wykonanie faktoryzacji Cholesky'ego na macierzy precyzji. Nie ma do tego klasy Bijectora; Jednakże CholeskyOuterProduct bijector wykonuje produkt 2 czynników Cholesky'iego. Możemy użyć odwrotność tej operacji przy użyciu Invert operatora.
2. Następnym krokiem jest wykonanie logu ukośnych elementów czynnika Choleskiego. Realizujemy to poprzez TransformDiagonal bijector i odwrotności Exp bijector.
3. W końcu spłaszcza dolną trójkątne części matrycy do wektora stosując odwrotność FillTriangular bijector.

# Our transform has 3 stages that we chain together via composition:
precision_to_unconstrained = tfb.Chain([
    # step 3: flatten the lower triangular portion of the matrix
    tfb.Invert(tfb.FillTriangular(validate_args=VALIDATE_ARGS)),
    # step 2: take the log of the diagonals    
    tfb.TransformDiagonal(tfb.Invert(tfb.Exp(validate_args=VALIDATE_ARGS))),
    # step 1: decompose the precision matrix into its Cholesky factors
    tfb.Invert(tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS)),
])

# sanity checks
m = tf.constant([[1., 2.], [2., 8.]])
m_fwd = precision_to_unconstrained.forward(m)
m_inv = precision_to_unconstrained.inverse(m_fwd)

# bijectors handle tensors of values, too!
m2 = tf.stack([m, tf.eye(2)])
m2_fwd = precision_to_unconstrained.forward(m2)
m2_inv = precision_to_unconstrained.inverse(m2_fwd)

print('single input:')
print('m:\n', m.numpy())
print('precision_to_unconstrained(m):\n', m_fwd.numpy())
print('inverse(precision_to_unconstrained(m)):\n', m_inv.numpy())
print()

print('tensor of inputs:')
print('m2:\n', m2.numpy())
print('precision_to_unconstrained(m2):\n', m2_fwd.numpy())
print('inverse(precision_to_unconstrained(m2)):\n', m2_inv.numpy())

single input:
m:
 [[1. 2.]
 [2. 8.]]
precision_to_unconstrained(m):
 [0.6931472 2.        0.       ]
inverse(precision_to_unconstrained(m)):
 [[1. 2.]
 [2. 8.]]

tensor of inputs:
m2:
 [[[1. 2.]
  [2. 8.]]

 [[1. 0.]
  [0. 1.]]]
precision_to_unconstrained(m2):
 [[0.6931472 2.        0.       ]
 [0.        0.        0.       ]]
inverse(precision_to_unconstrained(m2)):
 [[[1. 2.]
  [2. 8.]]

 [[1. 0.]
  [0. 1.]]]

TransformedDistribution klasa automatyzuje proces nakładania bijector do dystrybucji i podejmowania niezbędnych korekcji jakobian do log_prob() . Nasz nowy przeor staje się:

def log_lik_prior_transformed(transformed_precisions):
  rv_precision = tfd.TransformedDistribution(
      tfd.WishartTriL(
          df=PRIOR_DF,
          scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
          validate_args=VALIDATE_ARGS,
          allow_nan_stats=ALLOW_NAN_STATS),
      bijector=precision_to_unconstrained,
      validate_args=VALIDATE_ARGS)
  return rv_precision.log_prob(transformed_precisions)

# Check against the numpy implementation.  Note that when comparing, we need
# to add in the Jacobian correction.
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_prior_transformed(transformed_precisions).numpy()
corrections = precision_to_unconstrained.inverse_log_det_jacobian(
    transformed_precisions, event_ndims=1).numpy()
n = precisions.shape[0]

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
  print('tensorflow:', lik_tf[i])

0
numpy: -0.8488930160357633
tensorflow: -0.84889317
1
numpy: -7.305657151741624
tensorflow: -7.305659

Musimy tylko odwrócić transformację dla prawdopodobieństwa naszego dziennika danych:

precision = precision_to_unconstrained.inverse(transformed_precision)

Ponieważ faktycznie chcemy faktoryzacji Cholesky'ego macierzy precyzji, bardziej wydajne byłoby zrobienie tutaj tylko częściowej odwrotności. Jednak zostawimy optymalizację na później, a częściowe odwrócenie pozostawimy jako ćwiczenie dla czytelnika.

def log_lik_data_transformed(transformed_precisions, replicated_data):
  # We recover the precision matrix by inverting our bijector.  This is
  # inefficient since we really want the Cholesky decomposition of the
  # precision matrix, and the bijector has that in hand during the inversion,
  # but we'll worry about efficiency later.
  n = tf.shape(transformed_precisions)[0]
  precisions = precision_to_unconstrained.inverse(transformed_precisions)
  precisions_cholesky = tf.linalg.cholesky(precisions)
  covariances = tf.linalg.cholesky_solve(
      precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
  rv_data = tfd.MultivariateNormalFullCovariance(
      loc=tf.zeros([n, 2]),
      covariance_matrix=covariances,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)

  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# sanity check
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_data_transformed(
    transformed_precisions, replicated_data).numpy()

for i in range(precisions.shape[0]):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.8182

Ponownie zamykamy nasze nowe funkcje w zamknięciu.

def get_log_lik_transformed(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik_transformed(transformed_precisions):
    return (log_lik_data_transformed(transformed_precisions, replicated_data) +
            log_lik_prior_transformed(transformed_precisions))

  return _log_lik_transformed

# make sure everything runs
log_lik_fn = get_log_lik_transformed(my_data)
m = tf.eye(2)[tf.newaxis, ...]
lik = log_lik_fn(precision_to_unconstrained.forward(m)).numpy()
print(lik)

[-431.5611]

Próbowanie

Teraz, gdy nie musimy się martwić, że nasz sampler wysadzi się z powodu nieprawidłowych wartości parametrów, wygenerujmy kilka prawdziwych próbek.

Próbnik działa z nieograniczoną wersją naszych parametrów, więc musimy przekształcić naszą wartość początkową na jej nieograniczoną wersję. Wygenerowane przez nas próbki również będą miały nieograniczoną formę, więc musimy je z powrotem przekształcić. Bijektory są wektoryzowane, więc jest to łatwe.

# We'll choose a proper random initial value this time
np.random.seed(123)
initial_value_cholesky = np.array(
    [[0.5 + np.random.uniform(), 0.0],
     [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
    dtype=np.float32)
initial_value =  initial_value_cholesky.dot(
  initial_value_cholesky.T)[np.newaxis, ...]

# The sampler works with unconstrained values, so we'll transform our initial
# value
initial_value_transformed = precision_to_unconstrained.forward(
  initial_value).numpy()

# Sample!
@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_transformed(my_data, n_chains=1)

  num_results = 1000
  num_burnin_steps = 1000

  states, is_accepted = tfp.mcmc.sample_chain(
      num_results=num_results,
      num_burnin_steps=num_burnin_steps,
      current_state=[
          initial_value_transformed,
      ],
      kernel=tfp.mcmc.HamiltonianMonteCarlo(
          target_log_prob_fn=log_lik_fn,
          step_size=0.1,
          num_leapfrog_steps=3),
      trace_fn=lambda _, pkr: pkr.is_accepted,
      seed=123)
  # transform samples back to their constrained form
  precision_samples = [precision_to_unconstrained.inverse(s) for s in states]
  return states, precision_samples, is_accepted

states, precision_samples, is_accepted = sample()

Porównajmy średnią wyjścia naszego próbnika z analityczną średnią a posteriori!

print('True posterior mean:\n', posterior_mean)
print('Sample mean:\n', np.mean(np.reshape(precision_samples, [-1, 2, 2]), axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Sample mean:
 [[ 1.4315274  -0.25587553]
 [-0.25587553  0.5740424 ]]

Jesteśmy daleko! Dowiedzmy się dlaczego. Najpierw spójrzmy na nasze próbki.

np.reshape(precision_samples, [-1, 2, 2])

array([[[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       ...,

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]]], dtype=float32)

Och - wygląda na to, że wszystkie mają tę samą wartość. Dowiedzmy się dlaczego.

kernel_results_ zmienna to nazwana krotki, która daje informacje o sampler w każdym państwie. is_accepted pole jest kluczem tutaj.

# Look at the acceptance for the last 100 samples
print(np.squeeze(is_accepted)[-100:])
print('Fraction of samples accepted:', np.mean(np.squeeze(is_accepted)))

[False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False]
Fraction of samples accepted: 0.0

Wszystkie nasze próbki zostały odrzucone! Przypuszczalnie nasz rozmiar kroku był za duży. I wybrał stepsize=0.1 całkowicie dowolnie.

Wersja 3: próbkowanie z adaptacyjnym rozmiarem kroku

Ponieważ próbkowanie z moim arbitralnym wyborem wielkości kroku nie powiodło się, mamy kilka punktów agendy:

1. wdrożyć adaptacyjny rozmiar kroku i
2. przeprowadzić pewne testy zbieżności.

Istnieją pewne miłe przykładowy kod w tensorflow_probability/python/mcmc/hmc.py za wdrażanie adaptacyjnych rozmiary kroku. Zaadaptowałem to poniżej.

Należy pamiętać, że istnieje odrębny sess.run() oświadczenie na każdym kroku. Jest to bardzo pomocne przy debugowaniu, ponieważ w razie potrzeby pozwala nam łatwo dodać diagnostykę poszczególnych kroków. Na przykład możemy pokazać postępy, czas każdego kroku itp.

Wskazówka: Jeden najwyraźniej powszechny sposób bałagan próbkowania jest mieć swój wykres rosnąć w pętli. (Powodem sfinalizowania wykresu przed uruchomieniem sesji jest zapobieganie takim właśnie problemom.) Jeśli jednak nie używałeś finalize(), przydatnym sprawdzeniem debugowania, jeśli twój kod zwalnia do indeksowania, jest wydrukowanie wykresu rozmiar na każdym kroku poprzez len(mygraph.get_operations()) - jeśli wzrasta długość, jesteś prawdopodobnie robi coś złego.

Będziemy tu prowadzić 3 niezależne sieci. Przeprowadzenie pewnych porównań między łańcuchami pomoże nam sprawdzić zbieżność.

# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3

np.random.seed(123)

initial_values = []
for i in range(N_CHAINS):
  initial_value_cholesky = np.array(
      [[0.5 + np.random.uniform(), 0.0],
       [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
      dtype=np.float32)
  initial_values.append(initial_value_cholesky.dot(initial_value_cholesky.T))
initial_values = np.stack(initial_values)

initial_values_transformed = precision_to_unconstrained.forward(
  initial_values).numpy()

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_transformed(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=hmc,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states, is_accepted = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values_transformed,
      kernel=adapted_kernel,
      trace_fn=lambda _, pkr: pkr.inner_results.is_accepted,
      parallel_iterations=1)
  # transform samples back to their constrained form
  precision_samples = precision_to_unconstrained.inverse(states)
  return states, precision_samples, is_accepted

states, precision_samples, is_accepted = sample()

Szybkie sprawdzenie: nasz wskaźnik akceptacji podczas próbkowania jest bliski naszemu celowi 0,651.

print(np.mean(is_accepted))

0.6190666666666667

Co więcej, nasza średnia próbki i odchylenie standardowe są zbliżone do tego, czego oczekujemy od rozwiązania analitycznego.

precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.96426415 -1.6519215 ]
 [-1.6519215   3.8614824 ]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13622096 0.25235635]
 [0.25235635 0.5394968 ]]

Sprawdzanie konwergencji

Ogólnie rzecz biorąc, nie będziemy mieli rozwiązania analitycznego do sprawdzenia, więc musimy upewnić się, że próbnik osiągnął zbieżność. Jedna standardowa kontrola jest Gelman-Rubin \(\hat{R}\) statystyka, która wymaga wielu łańcuchów próbkowania. \(\hat{R}\) mierzy stopień, w jakim wariancji (środków) pomiędzy łańcuchami przekracza czego można by się spodziewać, jeśli łańcuchy były identycznie rozmieszczone. Wartości \(\hat{R}\) bliski 1 są wykorzystywane do wskazania przybliżeniu zbieżności. Zobacz źródło szczegóły.

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0038308 1.0005717]
 [1.0005717 1.0006068]]

Krytyka modeli

Gdybyśmy nie mieli rozwiązania analitycznego, byłby to czas na prawdziwą krytykę modelu.

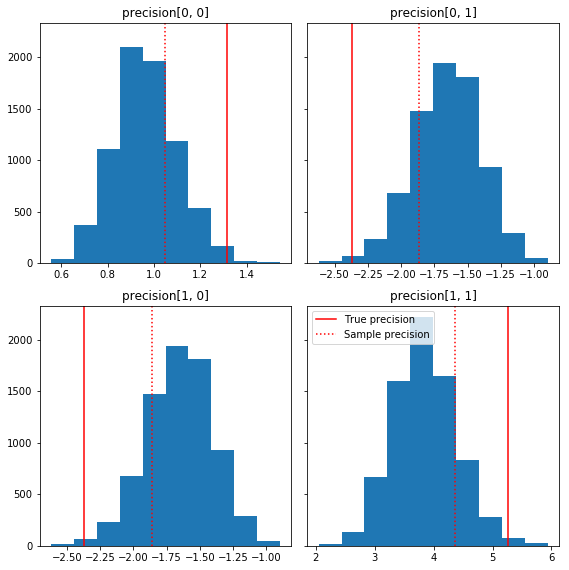
Oto kilka szybkich histogramów składników próbki w odniesieniu do naszej podstawowej prawdy (na czerwono). Należy zauważyć, że próbki zostały wcześniej skurczone od wartości macierzy dokładności próbki w kierunku macierzy identyfikacyjnej.

fig, axes = plt.subplots(2, 2, sharey=True)
fig.set_size_inches(8, 8)
for i in range(2):
  for j in range(2):
    ax = axes[i, j]
    ax.hist(precision_samples_reshaped[:, i, j])
    ax.axvline(true_precision[i, j], color='red',
               label='True precision')
    ax.axvline(sample_precision[i, j], color='red', linestyle=':',
               label='Sample precision')
    ax.set_title('precision[%d, %d]' % (i, j))
plt.tight_layout()
plt.legend()
plt.show()

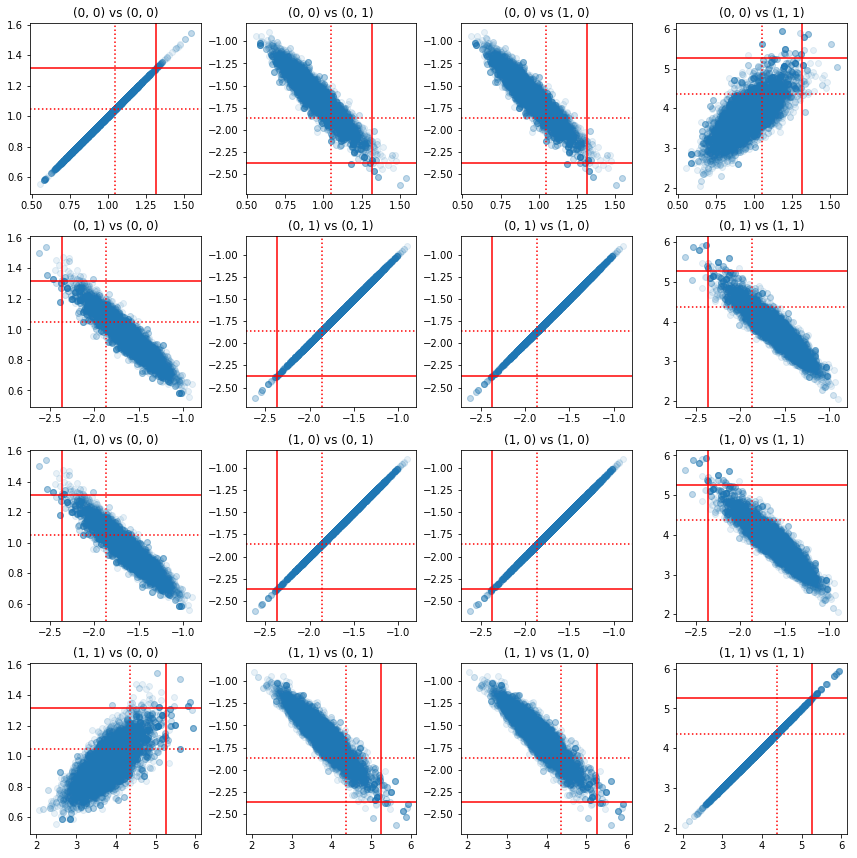
Niektóre wykresy rozrzutu par komponentów precyzji pokazują, że ze względu na strukturę korelacji a posteriori, rzeczywiste wartości a posteriori nie są tak nieprawdopodobne, jak wynikają z marginesów powyżej.

fig, axes = plt.subplots(4, 4)
fig.set_size_inches(12, 12)
for i1 in range(2):
  for j1 in range(2):
    index1 = 2 * i1 + j1
    for i2 in range(2):
      for j2 in range(2):
        index2 = 2 * i2 + j2
        ax = axes[index1, index2]
        ax.scatter(precision_samples_reshaped[:, i1, j1],
                   precision_samples_reshaped[:, i2, j2], alpha=0.1)
        ax.axvline(true_precision[i1, j1], color='red')
        ax.axhline(true_precision[i2, j2], color='red')
        ax.axvline(sample_precision[i1, j1], color='red', linestyle=':')
        ax.axhline(sample_precision[i2, j2], color='red', linestyle=':')
        ax.set_title('(%d, %d) vs (%d, %d)' % (i1, j1, i2, j2))
plt.tight_layout()
plt.show()

Wersja 4: prostsze próbkowanie ograniczonych parametrów

Bijektory sprawiły, że próbkowanie matrycy precyzji było proste, ale było sporo ręcznej konwersji do i z nieograniczonej reprezentacji. Jest prostszy sposób!

Przekształcone jądro przejściowe

TransformedTransitionKernel upraszcza ten proces. Owija twój sampler i obsługuje wszystkie konwersje. Jako argument przyjmuje listę bijektorów, które mapują nieograniczone wartości parametrów na ograniczone. Więc musimy odwrotność precision_to_unconstrained bijector użyliśmy powyżej. Mogliśmy po prostu użyć tfb.Invert(precision_to_unconstrained) , ale to wiązałoby biorąc od odwrotności odwrotności (TensorFlow nie jest wystarczająco inteligentny, aby uprościć tf.Invert(tf.Invert()) do tf.Identity()) , więc zamiast tego po prostu napiszę nowego bijectora.

Ograniczanie bijector

# The bijector we need for the TransformedTransitionKernel is the inverse of
# the one we used above
unconstrained_to_precision = tfb.Chain([
    # step 3: take the product of Cholesky factors
    tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS),
    # step 2: exponentiate the diagonals    
    tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
    # step 1: map a vector to a lower triangular matrix
    tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])

# quick sanity check
m = [[1., 2.], [2., 8.]]
m_inv = unconstrained_to_precision.inverse(m).numpy()
m_fwd = unconstrained_to_precision.forward(m_inv).numpy()

print('m:\n', m)
print('unconstrained_to_precision.inverse(m):\n', m_inv)
print('forward(unconstrained_to_precision.inverse(m)):\n', m_fwd)

m:
 [[1.0, 2.0], [2.0, 8.0]]
unconstrained_to_precision.inverse(m):
 [0.6931472 2.        0.       ]
forward(unconstrained_to_precision.inverse(m)):
 [[1. 2.]
 [2. 8.]]

Próbkowanie za pomocą TransformedTransitionKernel

Z TransformedTransitionKernel , nie musimy już robić ręcznie przekształceń naszych parametrów. Nasze wartości początkowe i nasze próbki są matrycami precyzji; musimy tylko przekazać nasze nieograniczające bijektory do jądra, a ono zajmie się wszystkimi transformacjami.

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  ttk = tfp.mcmc.TransformedTransitionKernel(
      inner_kernel=hmc, bijector=unconstrained_to_precision)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=ttk,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values,
      kernel=adapted_kernel,
      trace_fn=None,
      parallel_iterations=1)
  # transform samples back to their constrained form
  return states

precision_samples  = sample()

Sprawdzanie zbieżności

\(\hat{R}\) wygląd wyboru zbieżność dobre!

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0013582 1.0019467]
 [1.0019467 1.0011805]]

Porównanie z analitycznym tyłem

Znowu sprawdźmy analityczny tył.

# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])

print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.96687526 -1.6552585 ]
 [-1.6552585   3.867676  ]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13329624 0.24913791]
 [0.24913791 0.53983927]]

Optymalizacje

Teraz, gdy wszystko działa od początku do końca, zróbmy bardziej zoptymalizowaną wersję. W tym przykładzie szybkość nie ma większego znaczenia, ale gdy macierze będą większe, kilka optymalizacji zrobi dużą różnicę.

Jednym z dużych ulepszeń prędkości, jakie możemy zrobić, jest przeparametryzacja pod kątem rozkładu Choleskiego. Powodem jest to, że nasza funkcja wiarygodności danych wymaga zarówno macierzy kowariancji, jak i dokładności. Matrix inwersja jest drogie (\(O(n^3)\) za \(n \times n\) matrycy), a jeśli chodzi o parametryzacji albo kowariancji lub matrycy precyzji, musimy zrobić inwersję zdobycia drugiego.

Przypominamy, że prawdziwa, dodatnio określony, symetrycznych macierzy \(M\) może być rozłożona na produkt w postaci \(M = L L^T\) gdzie macierz \(L\) niższej trójkątny i ma pozytywny przekątnych. Ze względu na rozkład Cholesky'ego z \(M\), można bardziej skutecznie uzyskać zarówno \(M\) (produkt z dolną i górną matrycę trójkątny) i \(M^{-1}\) (przez podstawienie tyłu). Sama faktoryzacja Cholesky'ego nie jest tania do obliczenia, ale jeśli parametryzujemy pod względem czynników Cholesky'ego, musimy tylko obliczyć faktoryzację Choleksy'ego dla początkowych wartości parametrów.

Korzystanie z rozkładu Choleskiego macierzy kowariancji

TFP ma wersję wielowymiarowy rozkład normalny, MultivariateNormalTriL , że jest parametry- względem współczynnika Choleskiego macierzy kowariancji. Więc gdybyśmy mieli sparametryzować pod względem współczynnika Cholesky'ego macierzy kowariancji, moglibyśmy wydajnie obliczyć wiarygodność logarytmu danych. Wyzwanie polega na obliczeniu prawdopodobieństwa wcześniejszego dziennika z podobną wydajnością.

Gdybyśmy mieli wersję odwróconej dystrybucji Wisharta, która działała z czynnikami Cholesky'ego próbek, bylibyśmy wszyscy gotowi. Niestety nie. (Zespół chętnie przyjmie jednak przesłanie kodu!) Jako alternatywę możemy użyć wersji dystrybucji Wishart, która współpracuje z czynnikami Cholesky'ego próbek wraz z łańcuchem bijectorów.

W tej chwili brakuje nam kilku bijektorów, aby wszystko było naprawdę wydajne, ale chcę pokazać ten proces jako ćwiczenie i użyteczną ilustrację siły bijektorów TFP.

Dystrybucja Wishart, która działa na czynnikach Cholesky'ego

Wishart dystrybucja posiada użyteczną flagę, input_output_cholesky , który określa, że macierze wejściowe i wyjściowe powinny być czynniki Cholesky. Bardziej wydajna i liczbowo korzystna jest praca z czynnikami Cholesky'ego niż z pełnymi macierzami, dlatego jest to pożądane. Ważnym punktem na temat semantyki flagi: to tylko wskazanie, że reprezentacja wejściowych i wyjściowych do dystrybucji powinien zmienić - to nie wskazuje pełnego reparameterization dystrybucji, co wiązałoby się jakobian korektę do log_prob() funkcjonować. Właściwie chcemy dokonać pełnej reparametryzacji, więc zbudujemy naszą własną dystrybucję.

# An optimized Wishart distribution that has been transformed to operate on
# Cholesky factors instead of full matrices.  Note that we gain a modest
# additional speedup by specifying the Cholesky factor of the scale matrix
# (i.e. by passing in the scale_tril parameter instead of scale).

class CholeskyWishart(tfd.TransformedDistribution):
  """Wishart distribution reparameterized to use Cholesky factors."""
  def __init__(self,
      df,
      scale_tril,
      validate_args=False,
      allow_nan_stats=True,
      name='CholeskyWishart'):
    # Wishart has a bunch of methods that we want to support but not
    # implement.  We'll subclass TransformedDistribution here to take care of
    # those.  We'll override the few for which speed is critical and implement
    # them with a separate Wishart for which input_output_cholesky=True
    super(CholeskyWishart, self).__init__(
        distribution=tfd.WishartTriL(
            df=df,
            scale_tril=scale_tril,
            input_output_cholesky=False,
            validate_args=validate_args,
            allow_nan_stats=allow_nan_stats),
        bijector=tfb.Invert(tfb.CholeskyOuterProduct()),
        validate_args=validate_args,
        name=name
    )
    # Here's the Cholesky distribution we'll use for log_prob() and sample()
    self.cholesky = tfd.WishartTriL(
        df=df,
        scale_tril=scale_tril,
        input_output_cholesky=True,
        validate_args=validate_args,
        allow_nan_stats=allow_nan_stats)

  def _log_prob(self, x):
    return (self.cholesky.log_prob(x) +
            self.bijector.inverse_log_det_jacobian(x, event_ndims=2))

  def _sample_n(self, n, seed=None):
    return self.cholesky._sample_n(n, seed)

# some checks
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)

@tf.function(autograph=False)
def compute_log_prob(m):
  w_transformed = tfd.TransformedDistribution(
      tfd.WishartTriL(df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY),
      bijector=tfb.Invert(tfb.CholeskyOuterProduct()))
  w_optimized = CholeskyWishart(
      df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY)
  log_prob_transformed = w_transformed.log_prob(m)
  log_prob_optimized = w_optimized.log_prob(m)
  return log_prob_transformed, log_prob_optimized

for matrix in [np.eye(2, dtype=np.float32),
               np.array([[1., 0.], [2., 8.]], dtype=np.float32)]:
  log_prob_transformed, log_prob_optimized = [
      t.numpy() for t in compute_log_prob(matrix)]
  print('Transformed Wishart:', log_prob_transformed)
  print('Optimized Wishart', log_prob_optimized)

Transformed Wishart: -0.84889317
Optimized Wishart -0.84889317
Transformed Wishart: -99.269455
Optimized Wishart -99.269455

Budowanie odwrotnej dystrybucji Wishart

Mamy naszą macierz kowariancji \(C\) rozłożona na \(C = L L^T\) gdzie \(L\) jest niższa trójkątny i ma pozytywny przekątnej. Chcemy wiedzieć prawdopodobieństwo \(L\) danej że \(C \sim W^{-1}(\nu, V)\) gdzie \(W^{-1}\) jest odwrotnością dystrybucji Wishart.

Odwrotność dystrybucja Wishart ma tę właściwość, że jeśli \(C \sim W^{-1}(\nu, V)\), wtedy precyzja matryca \(C^{-1} \sim W(\nu, V^{-1})\). Więc możemy dostać prawdopodobieństwo \(L\) poprzez TransformedDistribution który przyjmuje jako parametry rozkładu Wishart i bijector który mapuje czynnik Choleskiego precyzji matrycy czynnik Choleskiego jego odwrotność.

Prosty (ale nie bardzo wydajne) sposób dostać się z czynnika Choleskiego z \(C^{-1}\) do \(L\) jest odwrócić współczynnik Choleskiego przez wstecznego rozwiązywania, a następnie tworząc macierz kowariancji z tych odwróconych czynników, a następnie robi faktoryzacji Choleskiego .

Niech rozkład choleskiego z \(C^{-1} = M M^T\). \(M\) jest niższa trójkątny, dzięki czemu możemy odwrócić go za pomocą MatrixInverseTriL bijector.

Formowanie \(C\) z \(M^{-1}\) jest trochę trudne: \(C = (M M^T)^{-1} = M^{-T}M^{-1} = M^{-T} (M^{-T})^T\). \(M\) jest mniejsza trójkątny, tak \(M^{-1}\) również będzie mniejsza trójkątny i \(M^{-T}\) będzie górnej trójkątnej. CholeskyOuterProduct() bijector działa tylko z dolnych trójkątnych matryc, więc nie można go użyć w celu utworzenia \(C\) z \(M^{-T}\). Nasze obejście to łańcuch bijectorów, który permutuje wiersze i kolumny macierzy.

Na szczęście ta logika jest zawarta w CholeskyToInvCholesky bijector!

Łącząc wszystkie kawałki

# verify that the bijector works
m = np.array([[1., 0.], [2., 8.]], dtype=np.float32)
c_inv = m.dot(m.T)
c = np.linalg.inv(c_inv)
c_chol = np.linalg.cholesky(c)
wishart_cholesky_to_iw_cholesky = tfb.CholeskyToInvCholesky()
w_fwd = wishart_cholesky_to_iw_cholesky.forward(m).numpy()

print('numpy =\n', c_chol)
print('bijector =\n', w_fwd)

numpy =
 [[ 1.0307764   0.        ]
 [-0.03031695  0.12126781]]
bijector =
 [[ 1.0307764   0.        ]
 [-0.03031695  0.12126781]]

Nasza ostateczna dystrybucja

Nasz odwrotny Wishart operujący na czynnikach Cholesky'ego wygląda następująco:

inverse_wishart_cholesky = tfd.TransformedDistribution(
    distribution=CholeskyWishart(
        df=PRIOR_DF,
        scale_tril=np.linalg.cholesky(np.linalg.inv(PRIOR_SCALE))),
    bijector=tfb.CholeskyToInvCholesky())

Mamy naszego odwrotnego Wisharta, ale jest to trochę powolne, ponieważ musimy dokonać rozkładu Cholesky'ego w bijectorze. Wróćmy do parametryzacji macierzy dokładności i zobaczmy, co możemy tam zrobić dla optymalizacji.

Wersja ostateczna(!): przy użyciu rozkładu Cholesky'ego macierzy precyzji

Alternatywnym podejściem jest praca z czynnikami Cholesky'ego macierzy precyzji. W tym przypadku funkcja prawdopodobieństwa a priori jest łatwa do obliczenia, ale funkcja prawdopodobieństwa dziennika danych wymaga więcej pracy, ponieważ TFP nie ma wersji wielowymiarowej wartości normalnej, która jest sparametryzowana przez precyzję.

Zoptymalizowane prawdopodobieństwo wcześniejszego logowania

Używamy CholeskyWishart dystrybucji mamy zbudowany nad skonstruować przeor.

# Our new prior.
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)

def log_lik_prior_cholesky(precisions_cholesky):
  rv_precision = CholeskyWishart(
      df=PRIOR_DF,
      scale_tril=PRIOR_SCALE_CHOLESKY,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)
  return rv_precision.log_prob(precisions_cholesky)

# Check against the slower TF implementation and the NumPy implementation.
# Note that when comparing to NumPy, we need to add in the Jacobian correction.
precisions = [np.eye(2, dtype=np.float32),
              true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
lik_tf = log_lik_prior_cholesky(precisions_cholesky).numpy()
lik_tf_slow = tfd.TransformedDistribution(
    distribution=tfd.WishartTriL(
        df=PRIOR_DF, scale_tril=tf.linalg.cholesky(PRIOR_SCALE)),
    bijector=tfb.Invert(tfb.CholeskyOuterProduct())).log_prob(
    precisions_cholesky).numpy()
corrections = tfb.Invert(tfb.CholeskyOuterProduct()).inverse_log_det_jacobian(
    precisions_cholesky, event_ndims=2).numpy()
n = precisions.shape[0]

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
  print('tensorflow slow:', lik_tf_slow[i])
  print('tensorflow fast:', lik_tf[i])

0
numpy: -0.8488930160357633
tensorflow slow: -0.84889317
tensorflow fast: -0.84889317
1
numpy: -7.442875031036973
tensorflow slow: -7.442877
tensorflow fast: -7.442876

Zoptymalizowane prawdopodobieństwo dziennika danych

We can use TFP's bijectors to build our own version of the multivariate normal. Here is the key idea:

Suppose I have a column vector \(X\) whose elements are iid samples of \(N(0, 1)\). We have \(\text{mean}(X) = 0\) and \(\text{cov}(X) = I\)

Now let \(Y = A X + b\). We have \(\text{mean}(Y) = b\) and \(\text{cov}(Y) = A A^T\)

Hence we can make vectors with mean \(b\) and covariance \(C\) using the affine transform \(Ax+b\) to vectors of iid standard Normal samples provided \(A A^T = C\). The Cholesky decomposition of \(C\) has the desired property. However, there are other solutions.

Let \(P = C^{-1}\) and let the Cholesky decomposition of \(P\) be \(B\), ie \(B B^T = P\). Now

\(P^{-1} = (B B^T)^{-1} = B^{-T} B^{-1} = B^{-T} (B^{-T})^T\)

So another way to get our desired mean and covariance is to use the affine transform \(Y=B^{-T}X + b\).

Our approach (courtesy of this notebook ):

1. Use tfd.Independent() to combine a batch of 1-D Normal random variables into a single multi-dimensional random variable. The reinterpreted_batch_ndims parameter for Independent() specifies the number of batch dimensions that should be reinterpreted as event dimensions. In our case we create a 1-D batch of length 2 that we transform into a 1-D event of length 2, so reinterpreted_batch_ndims=1 .
2. Apply a bijector to add the desired covariance: tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky, adjoint=True)) . Note that above we're multiplying our iid normal random variables by the transpose of the inverse of the Cholesky factor of the precision matrix \((B^{-T}X)\). The tfb.Invert takes care of inverting \(B\), and the adjoint=True flag performs the transpose.
3. Apply a bijector to add the desired offset: tfb.Shift(shift=shift) Note that we have to do the shift as a separate step from the initial inverted affine transform because otherwise the inverted scale is applied to the shift (since the inverse of \(y=Ax+b\) is \(x=A^{-1}y - A^{-1}b\)).

class MVNPrecisionCholesky(tfd.TransformedDistribution):
  """Multivariate normal parameterized by loc and Cholesky precision matrix."""

  def __init__(self, loc, precision_cholesky, name=None):
    super(MVNPrecisionCholesky, self).__init__(
        distribution=tfd.Independent(
            tfd.Normal(loc=tf.zeros_like(loc),
                       scale=tf.ones_like(loc)),
            reinterpreted_batch_ndims=1),
        bijector=tfb.Chain([
            tfb.Shift(shift=loc),
            tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky,
                                  adjoint=True)),
        ]),
        name=name)

@tf.function(autograph=False)
def log_lik_data_cholesky(precisions_cholesky, replicated_data):
  n = tf.shape(precisions_cholesky)[0]  # number of precision matrices
  rv_data = MVNPrecisionCholesky(
      loc=tf.zeros([n, 2]),
      precision_cholesky=precisions_cholesky)
  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# check against the numpy implementation
true_precision_cholesky = np.linalg.cholesky(true_precision)
precisions = [np.eye(2, dtype=np.float32), true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
n = precisions_cholesky.shape[0]
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
lik_tf = log_lik_data_cholesky(precisions_cholesky, replicated_data).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.81824

Combined log likelihood function

Now we combine our prior and data log likelihood functions in a closure.

def get_log_lik_cholesky(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik_cholesky(precisions_cholesky):
    return (log_lik_data_cholesky(precisions_cholesky, replicated_data) +
            log_lik_prior_cholesky(precisions_cholesky))

  return _log_lik_cholesky

Constraining bijector

Our samples are constrained to be valid Cholesky factors, which means they must be lower triangular matrices with positive diagonals. The TransformedTransitionKernel needs a bijector that maps unconstrained tensors to/from tensors with our desired constraints. We've removed the Cholesky decomposition from the bijector's inverse, which speeds things up.

unconstrained_to_precision_cholesky = tfb.Chain([
    # step 2: exponentiate the diagonals    
    tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
    # step 1: expand the vector to a lower triangular matrix
    tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])

# some checks
inv = unconstrained_to_precision_cholesky.inverse(precisions_cholesky).numpy()
fwd = unconstrained_to_precision_cholesky.forward(inv).numpy()
print('precisions_cholesky:\n', precisions_cholesky)
print('\ninv:\n', inv)
print('\nfwd(inv):\n', fwd)

precisions_cholesky:
 [[[ 1.         0.       ]
  [ 0.         1.       ]]

 [[ 1.1470785  0.       ]
  [-2.0647411  1.0000004]]]

inv:
 [[ 0.0000000e+00  0.0000000e+00  0.0000000e+00]
 [ 3.5762781e-07 -2.0647411e+00  1.3721828e-01]]

fwd(inv):
 [[[ 1.         0.       ]
  [ 0.         1.       ]]

 [[ 1.1470785  0.       ]
  [-2.0647411  1.0000004]]]

Initial values

We generate a tensor of initial values. We're working with Cholesky factors, so we generate some Cholesky factor initial values.

# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3

np.random.seed(123)

initial_values_cholesky = []
for i in range(N_CHAINS):
  initial_values_cholesky.append(np.array(
      [[0.5 + np.random.uniform(), 0.0],
       [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
      dtype=np.float32))
initial_values_cholesky = np.stack(initial_values_cholesky)

Sampling

We sample N_CHAINS chains using the TransformedTransitionKernel .

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_cholesky(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  ttk = tfp.mcmc.TransformedTransitionKernel(
      inner_kernel=hmc, bijector=unconstrained_to_precision_cholesky)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=ttk,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values,
      kernel=adapted_kernel,
      trace_fn=None,
      parallel_iterations=1)
  # transform samples back to their constrained form
  samples = tf.linalg.matmul(states, states, transpose_b=True)
  return samples

precision_samples = sample()

Convergence check

A quick convergence check looks good:

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0013583 1.0019467]
 [1.0019467 1.0011804]]

Comparing results to the analytic posterior

# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, newshape=[-1, 2, 2])

And again, the sample means and standard deviations match those of the analytic posterior.

print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.9668749 -1.6552604]
 [-1.6552604  3.8676758]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13329637 0.24913797]
 [0.24913797 0.53983945]]

Ok, all done! We've got our optimized sampler working.