 Lihat di TensorFlow.org Lihat di TensorFlow.org |  Jalankan di Google Colab Jalankan di Google Colab |  Lihat sumber di GitHub Lihat sumber di GitHub |  Unduh buku catatan Unduh buku catatan |
Saya menulis buku catatan ini sebagai studi kasus untuk mempelajari Probabilitas TensorFlow. Masalah yang saya pilih untuk dipecahkan adalah memperkirakan matriks kovarians untuk sampel variabel acak 0 Gaussian rata-rata 2-D. Masalahnya memiliki beberapa fitur bagus:
- Jika kita menggunakan invers Wishart prior untuk kovarians (pendekatan umum), masalahnya memiliki solusi analitik, sehingga kita dapat memeriksa hasil kita.
- Masalahnya melibatkan pengambilan sampel parameter yang dibatasi, yang menambahkan beberapa kompleksitas yang menarik.
- Solusi yang paling mudah bukanlah yang tercepat, jadi ada beberapa pekerjaan pengoptimalan yang harus dilakukan.
Saya memutuskan untuk menulis pengalaman saya sambil jalan. Butuh beberapa saat bagi saya untuk memahami poin-poin TFP yang lebih baik, jadi notebook ini memulai dengan cukup sederhana dan kemudian secara bertahap bekerja hingga fitur TFP yang lebih rumit. Saya mengalami banyak masalah di sepanjang jalan, dan saya telah mencoba menangkap proses yang membantu saya mengidentifikasi mereka dan solusi yang akhirnya saya temukan. Saya sudah mencoba untuk memasukkan banyak detail (termasuk banyak tes untuk memastikan langkah-langkah individu yang benar).
Mengapa mempelajari Probabilitas TensorFlow?
Saya menemukan Probabilitas TensorFlow menarik untuk proyek saya karena beberapa alasan:
- Probabilitas TensorFlow memungkinkan Anda membuat prototipe mengembangkan model kompleks secara interaktif di notebook. Anda dapat memecah kode Anda menjadi potongan-potongan kecil yang dapat Anda uji secara interaktif dan dengan pengujian unit.
- Setelah Anda siap untuk meningkatkan, Anda dapat memanfaatkan semua infrastruktur yang kami miliki untuk membuat TensorFlow berjalan di beberapa prosesor yang dioptimalkan di beberapa mesin.
- Akhirnya, meskipun saya sangat menyukai Stan, saya merasa cukup sulit untuk melakukan debug. Anda harus menulis semua kode pemodelan Anda dalam bahasa mandiri yang memiliki sedikit alat untuk memungkinkan Anda menyodok kode Anda, memeriksa status perantara, dan seterusnya.
Kelemahannya adalah TensorFlow Probability jauh lebih baru daripada Stan dan PyMC3, jadi dokumentasinya masih dalam proses, dan ada banyak fungsi yang belum dibangun. Untungnya, saya menemukan fondasi TFP kokoh, dan dirancang dengan cara modular yang memungkinkan seseorang untuk memperluas fungsinya dengan cukup mudah. Dalam buku catatan ini, selain menyelesaikan studi kasus, saya akan menunjukkan beberapa cara untuk memperluas TFP.
Untuk siapa ini?
Saya berasumsi bahwa pembaca datang ke buku catatan ini dengan beberapa prasyarat penting. Anda harus:
- Ketahui dasar-dasar inferensi Bayesian. (Jika Anda tidak, buku pertama yang benar-benar bagus adalah statistik Rethinking )
- Memiliki beberapa keakraban dengan pengambilan sampel perpustakaan MCMC, misalnya Stan / PyMC3 / BUG
- Memiliki pemahaman yang solid dari NumPy (Satu intro yang baik adalah Python untuk Analisis Data )
- Memiliki passing keakraban setidaknya dengan TensorFlow , tetapi tidak harus keahlian. ( Learning TensorFlow baik, tetapi berarti evolusi TensorFlow pesat yang sebagian besar buku akan sedikit tanggal. Stanford CS20 saja juga baik.)
Percobaan pertama
Inilah upaya pertama saya untuk mengatasi masalah tersebut. Spoiler: solusi saya tidak berhasil, dan perlu beberapa upaya untuk memperbaikinya! Meskipun prosesnya memakan waktu cukup lama, setiap upaya di bawah ini berguna untuk mempelajari bagian baru TFP.
Satu catatan: TFP saat ini tidak mengimplementasikan distribusi Wishart terbalik (kita akan melihat di bagian akhir bagaimana menggulung Wishart terbalik kita sendiri), jadi alih-alih saya akan mengubah masalahnya menjadi memperkirakan matriks presisi menggunakan Wishart sebelumnya.
import collections
import math
import os
import time
import numpy as np
import pandas as pd
import scipy
import scipy.stats
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
Langkah 1: kumpulkan pengamatannya
Data saya di sini semuanya sintetis, jadi ini akan tampak sedikit lebih rapi daripada contoh dunia nyata. Namun, tidak ada alasan Anda tidak dapat membuat beberapa data sintetis Anda sendiri.
Tip: Setelah Anda memutuskan pada bentuk model Anda, Anda dapat memilih beberapa nilai parameter dan menggunakan model yang dipilih untuk menghasilkan beberapa data sintetik. Sebagai pemeriksaan kewarasan penerapan Anda, Anda kemudian dapat memverifikasi bahwa perkiraan Anda menyertakan nilai sebenarnya dari parameter yang Anda pilih. Untuk membuat siklus debug/pengujian Anda lebih cepat, Anda dapat mempertimbangkan versi model yang disederhanakan (misalnya menggunakan lebih sedikit dimensi atau lebih sedikit sampel).
Tip: Ini paling mudah untuk bekerja dengan pengamatan Anda sebagai array NumPy. Satu hal penting yang perlu diperhatikan adalah NumPy secara default menggunakan float64, sedangkan TensorFlow secara default menggunakan float32.
Secara umum, operasi TensorFlow ingin semua argumen memiliki tipe yang sama, dan Anda harus melakukan transmisi data eksplisit untuk mengubah tipe. Jika Anda menggunakan pengamatan float64, Anda harus menambahkan banyak operasi cast. NumPy, sebaliknya, akan menangani casting secara otomatis. Oleh karena itu, jauh lebih mudah untuk mengkonversi data Numpy Anda ke float32 daripada memaksa TensorFlow penggunaan float64.
Pilih beberapa nilai parameter
# We're assuming 2-D data with a known true mean of (0, 0)
true_mean = np.zeros([2], dtype=np.float32)
# We'll make the 2 coordinates correlated
true_cor = np.array([[1.0, 0.9], [0.9, 1.0]], dtype=np.float32)
# And we'll give the 2 coordinates different variances
true_var = np.array([4.0, 1.0], dtype=np.float32)
# Combine the variances and correlations into a covariance matrix
true_cov = np.expand_dims(np.sqrt(true_var), axis=1).dot(
np.expand_dims(np.sqrt(true_var), axis=1).T) * true_cor
# We'll be working with precision matrices, so we'll go ahead and compute the
# true precision matrix here
true_precision = np.linalg.inv(true_cov)
# Here's our resulting covariance matrix
print(true_cov)
# Verify that it's positive definite, since np.random.multivariate_normal
# complains about it not being positive definite for some reason.
# (Note that I'll be including a lot of sanity checking code in this notebook -
# it's a *huge* help for debugging)
print('eigenvalues: ', np.linalg.eigvals(true_cov))
[[4. 1.8] [1.8 1. ]] eigenvalues: [4.843075 0.15692513]
Hasilkan beberapa pengamatan sintetis
Perhatikan bahwa TensorFlow Probabilitas menggunakan konvensi bahwa dimensi awal (s) data Anda mewakili indeks sampel, dan dimensi akhir (s) dari data Anda mewakili dimensi dari sampel Anda.
Di sini kami ingin 100 sampel, masing-masing adalah vektor panjang 2. Kami akan menghasilkan array my_data dengan bentuk (100, 2). my_data[i, :] adalah \(i\)sampel th, dan itu adalah vektor dengan panjang 2.
(Jangan lupa untuk membuat my_data memiliki jenis float32!)
# Set the seed so the results are reproducible.
np.random.seed(123)
# Now generate some observations of our random variable.
# (Note that I'm suppressing a bunch of spurious about the covariance matrix
# not being positive semidefinite via check_valid='ignore' because it really is
# positive definite!)
my_data = np.random.multivariate_normal(
mean=true_mean, cov=true_cov, size=100,
check_valid='ignore').astype(np.float32)
my_data.shape
(100, 2)
Kewarasan memeriksa pengamatan
Salah satu sumber bug potensial adalah mengacaukan data sintetis Anda! Mari kita lakukan beberapa pemeriksaan sederhana.
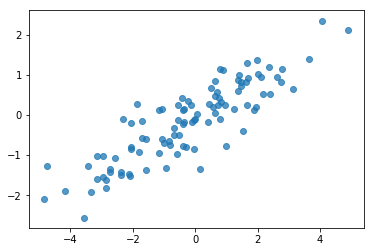
# Do a scatter plot of the observations to make sure they look like what we
# expect (higher variance on the x-axis, y values strongly correlated with x)
plt.scatter(my_data[:, 0], my_data[:, 1], alpha=0.75)
plt.show()
print('mean of observations:', np.mean(my_data, axis=0))
print('true mean:', true_mean)
mean of observations: [-0.24009615 -0.16638893] true mean: [0. 0.]
print('covariance of observations:\n', np.cov(my_data, rowvar=False))
print('true covariance:\n', true_cov)
covariance of observations: [[3.95307734 1.68718486] [1.68718486 0.94910269]] true covariance: [[4. 1.8] [1.8 1. ]]
Oke, sampel kami terlihat masuk akal. Langkah berikutnya.
Langkah 2: Terapkan fungsi kemungkinan di NumPy
Hal utama yang perlu kita tulis untuk melakukan pengambilan sampel MCMC di TF Probability adalah fungsi kemungkinan log. Secara umum menulis TF sedikit lebih sulit daripada NumPy, jadi saya merasa terbantu untuk melakukan implementasi awal di NumPy. Aku akan membagi fungsi kemungkinan menjadi 2 buah, fungsi data yang kemungkinan dapat disamakan dengan \(P(data | parameters)\) dan fungsi kemungkinan sebelumnya yang bersesuaian dengan \(P(parameters)\).
Perhatikan bahwa fungsi NumPy ini tidak harus super dioptimalkan / divektorkan karena tujuannya hanya untuk menghasilkan beberapa nilai untuk pengujian. Kebenaran adalah pertimbangan utama!
Pertama kita akan mengimplementasikan bagian kemungkinan log data. Itu cukup mudah. Satu hal yang perlu diingat adalah kita akan bekerja dengan matriks presisi, jadi kita akan membuat parameter yang sesuai.
def log_lik_data_numpy(precision, data):
# np.linalg.inv is a really inefficient way to get the covariance matrix, but
# remember we don't care about speed here
cov = np.linalg.inv(precision)
rv = scipy.stats.multivariate_normal(true_mean, cov)
return np.sum(rv.logpdf(data))
# test case: compute the log likelihood of the data given the true parameters
log_lik_data_numpy(true_precision, my_data)
-280.81822950593767
Kita akan menggunakan Wishart sebelumnya untuk matriks presisi karena ada solusi analitis untuk posterior (lihat tabel berguna Wikipedia dari prior konjugat ).
The distribusi Wishart memiliki 2 parameter:
- jumlah derajat kebebasan (berlabel \(\nu\) di Wikipedia)
- matriks skala (berlabel \(V\) di Wikipedia)
Mean untuk distribusi Wishart dengan parameter \(\nu, V\) adalah \(E[W] = \nu V\), dan varians adalah \(\text{Var}(W_{ij}) = \nu(v_{ij}^2+v_{ii}v_{jj})\)
Beberapa intuisi yang berguna: Anda dapat menghasilkan Wishart sampel dengan menghasilkan \(\nu\) independen menarik \(x_1 \ldots x_{\nu}\) dari variabel acak normal multivariat dengan mean 0 dan covariance \(V\) dan kemudian membentuk jumlah \(W = \sum_{i=1}^{\nu} x_i x_i^T\).
Jika Anda rescale sampel Wishart dengan membagi mereka dengan \(\nu\), Anda mendapatkan matriks kovarians sampel \(x_i\). Matriks kovarians sampel ini harus cenderung ke arah \(V\) sebagai \(\nu\) meningkat. Ketika \(\nu\) kecil, ada banyak variasi dalam matriks kovarians sampel, nilai-nilai sehingga kecil \(\nu\) sesuai dengan prior lemah dan nilai-nilai besar \(\nu\) sesuai dengan prior kuat. Perhatikan bahwa \(\nu\) harus setidaknya sama besar dengan dimensi ruang yang Anda sampel sedang atau Anda akan menghasilkan matriks singular.
Kami akan menggunakan \(\nu = 3\) sehingga kami memiliki lemah sebelumnya, dan kami akan mengambil \(V = \frac{1}{\nu} I\) yang akan menarik estimasi kovarians kita terhadap identitas (recall yang rata-rata adalah \(\nu V\)).
PRIOR_DF = 3
PRIOR_SCALE = np.eye(2, dtype=np.float32) / PRIOR_DF
def log_lik_prior_numpy(precision):
rv = scipy.stats.wishart(df=PRIOR_DF, scale=PRIOR_SCALE)
return rv.logpdf(precision)
# test case: compute the prior for the true parameters
log_lik_prior_numpy(true_precision)
-9.103606346649766
Wishart distribusi adalah sebelum konjugasi untuk memperkirakan matriks ketepatan normal multivariat dengan dikenal rata \(\mu\).
Misalkan parameter Wishart sebelumnya yang \(\nu, V\) dan bahwa kita memiliki \(n\) pengamatan multivariat normal, kami \(x_1, \ldots, x_n\). Parameter posterior yang \(n + \nu, \left(V^{-1} + \sum_{i=1}^n (x_i-\mu)(x_i-\mu)^T \right)^{-1}\).
n = my_data.shape[0]
nu_prior = PRIOR_DF
v_prior = PRIOR_SCALE
nu_posterior = nu_prior + n
v_posterior = np.linalg.inv(np.linalg.inv(v_prior) + my_data.T.dot(my_data))
posterior_mean = nu_posterior * v_posterior
v_post_diag = np.expand_dims(np.diag(v_posterior), axis=1)
posterior_sd = np.sqrt(nu_posterior *
(v_posterior ** 2.0 + v_post_diag.dot(v_post_diag.T)))
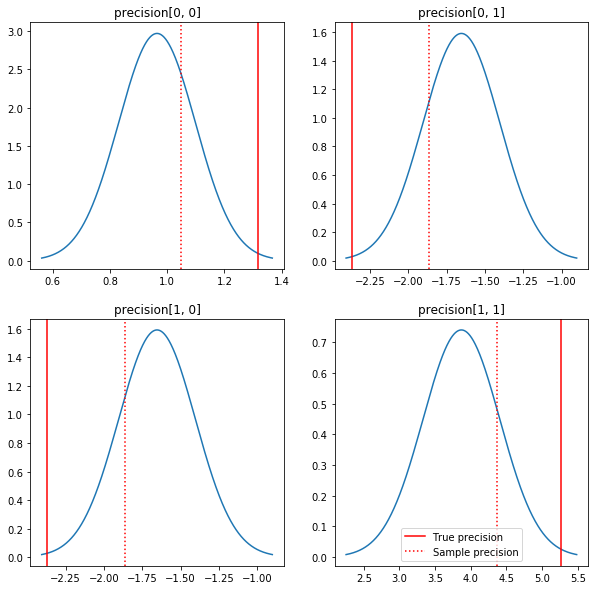
Plot cepat posterior dan nilai sebenarnya. Perhatikan bahwa posterior dekat dengan sampel posterior tetapi sedikit menyusut ke arah identitas. Perhatikan juga bahwa nilai sebenarnya cukup jauh dari mode posterior - mungkin ini karena prior tidak cocok dengan data kita. Dalam masalah nyata kita mungkin akan melakukan lebih baik dengan sesuatu seperti skala terbalik Wishart sebelum untuk kovarians (lihat, misalnya, Andrew Gelman ini komentar pada subjek), tapi kemudian kita tidak akan memiliki posterior analitik bagus.
sample_precision = np.linalg.inv(np.cov(my_data, rowvar=False, bias=False))
fig, axes = plt.subplots(2, 2)
fig.set_size_inches(10, 10)
for i in range(2):
for j in range(2):
ax = axes[i, j]
loc = posterior_mean[i, j]
scale = posterior_sd[i, j]
xmin = loc - 3.0 * scale
xmax = loc + 3.0 * scale
x = np.linspace(xmin, xmax, 1000)
y = scipy.stats.norm.pdf(x, loc=loc, scale=scale)
ax.plot(x, y)
ax.axvline(true_precision[i, j], color='red', label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':', label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.legend()
plt.show()
Langkah 3: Terapkan fungsi kemungkinan di TensorFlow
Spoiler: Upaya pertama kami tidak akan berhasil; kita akan berbicara tentang mengapa di bawah ini.
Tip: Penggunaan TensorFlow bersemangat modus ketika mengembangkan fungsi kemungkinan Anda. Modus ingin membuat TF berperilaku lebih seperti NumPy - semuanya mengeksekusi segera, sehingga Anda dapat men-debug secara interaktif daripada harus menggunakan Session.run() . Lihat catatan di sini .
Pendahuluan: Kelas distribusi
TFP memiliki kumpulan kelas distribusi yang akan kita gunakan untuk menghasilkan probabilitas log kita. Satu hal yang perlu diperhatikan adalah bahwa kelas-kelas ini bekerja dengan tensor sampel, bukan hanya sampel tunggal - ini memungkinkan untuk vektorisasi dan percepatan terkait.
Distribusi dapat bekerja dengan tensor sampel dalam 2 cara berbeda. Ini paling sederhana untuk menggambarkan 2 cara ini dengan contoh nyata yang melibatkan distribusi dengan parameter skalar tunggal. Saya akan menggunakan Poisson distribusi, yang memiliki rate parameter.
- Jika kita membuat Poisson dengan nilai tunggal untuk
rateparameter, panggilan untuk nyasample()metode mengembalikan nilai tunggal. Nilai ini disebutevent, dan dalam hal ini peristiwa semua skalar. - Jika kita membuat Poisson dengan tensor nilai untuk
rateparameter, panggilan untuk nyasample()metode sekarang kembali beberapa nilai, satu untuk setiap nilai dalam tensor tingkat. Objek bertindak sebagai koleksi Poissons independen, masing-masing dengan tingkat sendiri, dan masing-masing dari nilai-nilai yang dikembalikan oleh panggilan untuksample()berkorespondensi ke salah satu Poissons ini. Koleksi ini independen tapi tidak peristiwa terdistribusi secara identik disebutbatch. - The
sample()metode mengambilsample_shapeparameter yang default ke tupel kosong. Melewati nilai non-kosong untuksample_shapehasil dalam sampel kembali beberapa batch. Koleksi ini dari batch disebutsample.
Sebuah distribusi ini log_prob() metode mengkonsumsi data dengan cara yang paralel bagaimana sample() menghasilkan itu. log_prob() mengembalikan probabilitas untuk sampel, yaitu untuk beberapa, batch independen peristiwa.
- Jika kita memiliki objek Poisson kami yang telah dibuat dengan skalar
rate, setiap batch adalah skalar, dan jika kita lulus dalam tensor sampel, kita akan mendapatkan sebuah tensor dengan ukuran yang sama probabilitas log. - Jika kita memiliki objek Poisson kami yang telah dibuat dengan tensor bentuk
Tdariratenilai-nilai, setiap batch adalah tensor bentukT. Jika kita melewatkan tensor sampel bentuk D, T, kita akan mendapatkan tensor probabilitas log bentuk D, T.
Di bawah ini adalah beberapa contoh yang menggambarkan kasus-kasus ini. Lihat notebook ini untuk tutorial lebih rinci tentang peristiwa, batch, dan bentuk.
# case 1: get log probabilities for a vector of iid draws from a single
# normal distribution
norm1 = tfd.Normal(loc=0., scale=1.)
probs1 = norm1.log_prob(tf.constant([1., 0.5, 0.]))
# case 2: get log probabilities for a vector of independent draws from
# multiple normal distributions with different parameters. Note the vector
# values for loc and scale in the Normal constructor.
norm2 = tfd.Normal(loc=[0., 2., 4.], scale=[1., 1., 1.])
probs2 = norm2.log_prob(tf.constant([1., 0.5, 0.]))
print('iid draws from a single normal:', probs1.numpy())
print('draws from a batch of normals:', probs2.numpy())
iid draws from a single normal: [-1.4189385 -1.0439385 -0.9189385] draws from a batch of normals: [-1.4189385 -2.0439386 -8.918939 ]
Kemungkinan log data
Pertama kita akan mengimplementasikan fungsi kemungkinan log data.
VALIDATE_ARGS = True
ALLOW_NAN_STATS = False
Satu perbedaan utama dari kasus NumPy adalah bahwa fungsi kemungkinan TensorFlow kami perlu menangani vektor matriks presisi, bukan hanya matriks tunggal. Vektor parameter akan digunakan ketika kita mengambil sampel dari beberapa rantai.
Kami akan membuat objek distribusi yang bekerja dengan sekumpulan matriks presisi (yaitu satu matriks per rantai).
Saat menghitung probabilitas log data kami, kami memerlukan data kami untuk direplikasi dengan cara yang sama seperti parameter kami sehingga ada satu salinan per variabel batch. Bentuk data yang direplikasi harus sebagai berikut:
[sample shape, batch shape, event shape]
Dalam kasus kami, bentuk acaranya adalah 2 (karena kami bekerja dengan Gauss 2-D). Bentuk sampel adalah 100, karena kami memiliki 100 sampel. Bentuk batch hanya akan menjadi jumlah matriks presisi yang sedang kita kerjakan. Percuma untuk mereplikasi data setiap kali kita memanggil fungsi kemungkinan, jadi kita akan mereplikasi data terlebih dahulu dan meneruskan versi yang direplikasi.
Perhatikan bahwa ini merupakan implementasi tidak efisien: MultivariateNormalFullCovariance relatif mahal untuk beberapa alternatif yang akan kita bicarakan di bagian optimasi di akhir.
def log_lik_data(precisions, replicated_data):
n = tf.shape(precisions)[0] # number of precision matrices
# We're estimating a precision matrix; we have to invert to get log
# probabilities. Cholesky inversion should be relatively efficient,
# but as we'll see later, it's even better if we can avoid doing the Cholesky
# decomposition altogether.
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# For our test, we'll use a tensor of 2 precision matrices.
# We'll need to replicate our data for the likelihood function.
# Remember, TFP wants the data to be structured so that the sample dimensions
# are first (100 here), then the batch dimensions (2 here because we have 2
# precision matrices), then the event dimensions (2 because we have 2-D
# Gaussian data). We'll need to add a middle dimension for the batch using
# expand_dims, and then we'll need to create 2 replicates in this new dimension
# using tile.
n = 2
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
print(replicated_data.shape)
(100, 2, 2)
Tip: Satu hal yang saya telah menemukan untuk menjadi sangat membantu menulis cek kewarasan sedikit fungsi TensorFlow saya. Sangat mudah untuk mengacaukan vektorisasi di TF, jadi memiliki fungsi NumPy yang lebih sederhana adalah cara yang bagus untuk memverifikasi keluaran TF. Anggap ini sebagai tes unit kecil.
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_data(precisions, replicated_data=replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
Kemungkinan log sebelumnya
Prioritas lebih mudah karena kita tidak perlu khawatir tentang replikasi data.
@tf.function(autograph=False)
def log_lik_prior(precisions):
rv_precision = tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions)
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_prior(precisions).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]))
print('tensorflow:', lik_tf[i])
0 numpy: -2.2351873809649625 tensorflow: -2.2351875 1 numpy: -9.103606346649766 tensorflow: -9.103608
Bangun fungsi kemungkinan log bersama
Fungsi kemungkinan log data di atas bergantung pada pengamatan kami, tetapi pengambil sampel tidak akan memilikinya. Kita dapat menghilangkan ketergantungan tanpa menggunakan variabel global dengan menggunakan [penutupan](https://en.wikipedia.org/wiki/Closure_(computer_programming). Penutupan melibatkan fungsi luar yang membangun lingkungan yang berisi variabel yang dibutuhkan oleh fungsi batin.
def get_log_lik(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik(precision):
return log_lik_data(precision, replicated_data) + log_lik_prior(precision)
return _log_lik
Langkah 4: Contoh
Oke, saatnya untuk sampel! Untuk mempermudah, kita hanya akan menggunakan 1 rantai dan kita akan menggunakan matriks identitas sebagai titik awal. Kami akan melakukan hal-hal lebih hati-hati nanti.
Sekali lagi, ini tidak akan berhasil - kita akan mendapatkan pengecualian.
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.expand_dims(tf.eye(2), axis=0)
# Use expand_dims because we want to pass in a tensor of starting values
log_lik_fn = get_log_lik(my_data, n_chains=1)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
return states
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
Cholesky decomposition was not successful. The input might not be valid.
[[{ {node mcmc_sample_chain/trace_scan/while/body/_79/smart_for_loop/while/body/_371/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_537/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/StatefulPartitionedCall/Cholesky} }]] [Op:__inference_sample_2849]
Function call stack:
sample
...
Function call stack:
sample
Mengidentifikasi masalah
InvalidArgumentError (see above for traceback): Cholesky decomposition was not successful. The input might not be valid. Itu tidak terlalu membantu. Mari kita lihat apakah kita dapat mengetahui lebih banyak tentang apa yang terjadi.
- Kami akan mencetak parameter untuk setiap langkah sehingga kami dapat melihat nilai yang gagal
- Kami akan menambahkan beberapa pernyataan untuk menghindari masalah tertentu.
Pernyataan rumit karena merupakan operasi TensorFlow, dan kita harus berhati-hati agar pernyataan tersebut dieksekusi dan tidak dioptimalkan di luar grafik. Itu layak membaca gambaran ini dari TensorFlow debugging jika Anda tidak akrab dengan pernyataan TF. Anda secara eksplisit dapat memaksa pernyataan untuk mengeksekusi menggunakan tf.control_dependencies (lihat komentar dalam kode di bawah).
Asli TensorFlow ini Print fungsi memiliki perilaku yang sama seperti pernyataan - itu operasi, dan Anda perlu mengambil beberapa perawatan untuk memastikan bahwa dijalankan. Print menyebabkan sakit kepala tambahan ketika kita sedang bekerja di sebuah notebook: outputnya dikirim ke stderr , dan stderr tidak ditampilkan dalam sel. Kami akan menggunakan tipuan di sini: alih-alih menggunakan tf.Print , kami akan membuat operasi TensorFlow cetak kita sendiri melalui tf.pyfunc . Seperti halnya pernyataan, kita harus memastikan metode kita dieksekusi.
def get_log_lik_verbose(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
def _log_lik(precisions):
# An internal method we'll make into a TensorFlow operation via tf.py_func
def _print_precisions(precisions):
print('precisions:\n', precisions)
return False # operations must return something!
# Turn our method into a TensorFlow operation
print_op = tf.compat.v1.py_func(_print_precisions, [precisions], tf.bool)
# Assertions are also operations, and some care needs to be taken to ensure
# that they're executed
assert_op = tf.assert_equal(
precisions, tf.linalg.matrix_transpose(precisions),
message='not symmetrical', summarize=4, name='symmetry_check')
# The control_dependencies statement forces its arguments to be executed
# before subsequent operations
with tf.control_dependencies([print_op, assert_op]):
return (log_lik_data(precisions, replicated_data) +
log_lik_prior(precisions))
return _log_lik
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.eye(2)[tf.newaxis, ...]
log_lik_fn = get_log_lik_verbose(my_data)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[ 0.24315196 -0.2761638 ]
[-0.33882257 0.8622 ]]]
assertion failed: [not symmetrical] [Condition x == y did not hold element-wise:] [x (leapfrog_integrate_one_step/add:0) = ] [[[0.243151963 -0.276163787][-0.338822573 0.8622]]] [y (leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/matrix_transpose/transpose:0) = ] [[[0.243151963 -0.338822573][-0.276163787 0.8622]]]
[[{ {node mcmc_sample_chain/trace_scan/while/body/_96/smart_for_loop/while/body/_381/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_503/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/symmetry_check_1/Assert/AssertGuard/else/_577/Assert} }]] [Op:__inference_sample_4837]
Function call stack:
sample
...
Function call stack:
sample
Mengapa ini gagal?
Nilai parameter baru pertama yang dicoba oleh sampler adalah matriks asimetris. Itu menyebabkan dekomposisi Cholesky gagal, karena itu hanya didefinisikan untuk matriks simetris (dan pasti positif).
Masalahnya di sini adalah bahwa parameter yang diinginkan adalah matriks presisi, dan matriks presisi harus nyata, simetris, dan pasti positif. Sampler tidak tahu apa-apa tentang batasan ini (kecuali mungkin melalui gradien), jadi sangat mungkin sampler akan mengusulkan nilai yang tidak valid, yang mengarah ke pengecualian, terutama jika ukuran langkahnya besar.
Dengan sampler Hamiltonian Monte Carlo, kita mungkin dapat mengatasi masalah dengan menggunakan ukuran langkah yang sangat kecil, karena gradien harus menjauhkan parameter dari daerah yang tidak valid, tetapi ukuran langkah kecil berarti konvergensi lambat. Dengan sampler Metropolis-Hastings, yang tidak tahu apa-apa tentang gradien, kita akan gagal.
Versi 2: reparametrizing ke parameter yang tidak dibatasi
Ada solusi langsung untuk masalah di atas: kita dapat memparameterisasi ulang model kita sedemikian rupa sehingga parameter baru tidak lagi memiliki kendala ini. TFP menyediakan seperangkat alat yang berguna - bijector - untuk melakukan hal itu.
Parameterisasi ulang dengan bijector
Matriks presisi kita harus nyata dan simetris; kami menginginkan parameterisasi alternatif yang tidak memiliki batasan ini. Titik awal adalah faktorisasi Cholesky dari matriks presisi. Faktor Cholesky masih dibatasi - mereka adalah segitiga bawah, dan elemen diagonalnya harus positif. Namun, jika kita mengambil log diagonal dari faktor Cholesky, log tidak lagi dibatasi menjadi positif, dan kemudian jika kita meratakan bagian segitiga bawah menjadi vektor 1-D, kita tidak lagi memiliki kendala segitiga bawah. . Hasil dalam kasus kami akan menjadi vektor panjang 3 tanpa kendala.
(The pengguna Stan memiliki bab besar pada menggunakan transformasi untuk menghilangkan berbagai jenis kendala pada parameter.)
Parameterisasi ulang ini memiliki sedikit efek pada fungsi kemungkinan log data kami - kami hanya perlu membalikkan transformasi kami sehingga kami mendapatkan kembali matriks presisi - tetapi efek pada sebelumnya lebih rumit. Kami telah menetapkan bahwa probabilitas matriks presisi yang diberikan diberikan oleh distribusi Wishart; berapa peluang matriks yang ditransformasi?
Ingat bahwa jika kita menerapkan fungsi monoton \(g\) ke 1-D variabel acak \(X\), \(Y = g(X)\), kepadatan untuk \(Y\) diberikan oleh
\[ f_Y(y) = | \frac{d}{dy}(g^{-1}(y)) | f_X(g^{-1}(y)) \]
Turunan dari \(g^{-1}\) jangka menyumbang cara \(g\) perubahan volume lokal. Untuk variabel acak dimensi yang lebih tinggi, faktor koreksi adalah nilai absolut dari determinan Jacobian dari \(g^{-1}\) (lihat di sini ).
Kita harus menambahkan Jacobian dari transformasi terbalik ke dalam fungsi kemungkinan log sebelumnya. Untungnya, TFP ini Bijector kelas bisa mengurus ini bagi kita.
The Bijector kelas digunakan untuk mewakili dibalik, fungsi halus yang digunakan untuk mengubah variabel dalam fungsi kepadatan probabilitas. Bijectors semua memiliki forward() metode yang melakukan transformasi, sebuah inverse() metode yang membalikkan itu, dan forward_log_det_jacobian() dan inverse_log_det_jacobian() metode yang memberikan koreksi Jacobian kita butuhkan ketika kita reparaterize pdf.
TFP menyediakan koleksi bijectors berguna yang kita dapat menggabungkan melalui komposisi melalui Chain operator untuk membentuk transformasi cukup rumit. Dalam kasus kami, kami akan membuat 3 bijector berikut (operasi dalam rantai dilakukan dari kanan ke kiri):
- Langkah pertama dari transformasi kami adalah melakukan faktorisasi Cholesky pada matriks presisi. Tidak ada kelas Bijector untuk itu; Namun,
CholeskyOuterProductbijector mengambil produk dari 2 faktor Cholesky. Kita dapat menggunakan kebalikan dari yang operasi menggunakanInvertoperator. - Langkah selanjutnya adalah mengambil log elemen diagonal dari faktor Cholesky. Kami mencapai ini melalui
TransformDiagonalbijector dan kebalikan dariExpbijector. - Akhirnya kami meratakan bagian segitiga bawah dari matriks ke vektor menggunakan kebalikan dari
FillTriangularbijector.
# Our transform has 3 stages that we chain together via composition:
precision_to_unconstrained = tfb.Chain([
# step 3: flatten the lower triangular portion of the matrix
tfb.Invert(tfb.FillTriangular(validate_args=VALIDATE_ARGS)),
# step 2: take the log of the diagonals
tfb.TransformDiagonal(tfb.Invert(tfb.Exp(validate_args=VALIDATE_ARGS))),
# step 1: decompose the precision matrix into its Cholesky factors
tfb.Invert(tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS)),
])
# sanity checks
m = tf.constant([[1., 2.], [2., 8.]])
m_fwd = precision_to_unconstrained.forward(m)
m_inv = precision_to_unconstrained.inverse(m_fwd)
# bijectors handle tensors of values, too!
m2 = tf.stack([m, tf.eye(2)])
m2_fwd = precision_to_unconstrained.forward(m2)
m2_inv = precision_to_unconstrained.inverse(m2_fwd)
print('single input:')
print('m:\n', m.numpy())
print('precision_to_unconstrained(m):\n', m_fwd.numpy())
print('inverse(precision_to_unconstrained(m)):\n', m_inv.numpy())
print()
print('tensor of inputs:')
print('m2:\n', m2.numpy())
print('precision_to_unconstrained(m2):\n', m2_fwd.numpy())
print('inverse(precision_to_unconstrained(m2)):\n', m2_inv.numpy())
single input: m: [[1. 2.] [2. 8.]] precision_to_unconstrained(m): [0.6931472 2. 0. ] inverse(precision_to_unconstrained(m)): [[1. 2.] [2. 8.]] tensor of inputs: m2: [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]] precision_to_unconstrained(m2): [[0.6931472 2. 0. ] [0. 0. 0. ]] inverse(precision_to_unconstrained(m2)): [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]]
The TransformedDistribution kelas mengotomatiskan proses menerapkan bijector untuk distribusi dan membuat koreksi Jacobian yang diperlukan untuk log_prob() . Prior baru kami menjadi:
def log_lik_prior_transformed(transformed_precisions):
rv_precision = tfd.TransformedDistribution(
tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS),
bijector=precision_to_unconstrained,
validate_args=VALIDATE_ARGS)
return rv_precision.log_prob(transformed_precisions)
# Check against the numpy implementation. Note that when comparing, we need
# to add in the Jacobian correction.
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_prior_transformed(transformed_precisions).numpy()
corrections = precision_to_unconstrained.inverse_log_det_jacobian(
transformed_precisions, event_ndims=1).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow: -0.84889317 1 numpy: -7.305657151741624 tensorflow: -7.305659
Kami hanya perlu membalikkan transformasi untuk kemungkinan log data kami:
precision = precision_to_unconstrained.inverse(transformed_precision)
Karena kita sebenarnya menginginkan faktorisasi Cholesky dari matriks presisi, akan lebih efisien untuk melakukan invers parsial saja di sini. Namun, kami akan meninggalkan pengoptimalan untuk nanti dan akan meninggalkan invers parsial sebagai latihan untuk pembaca.
def log_lik_data_transformed(transformed_precisions, replicated_data):
# We recover the precision matrix by inverting our bijector. This is
# inefficient since we really want the Cholesky decomposition of the
# precision matrix, and the bijector has that in hand during the inversion,
# but we'll worry about efficiency later.
n = tf.shape(transformed_precisions)[0]
precisions = precision_to_unconstrained.inverse(transformed_precisions)
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# sanity check
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_data_transformed(
transformed_precisions, replicated_data).numpy()
for i in range(precisions.shape[0]):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
Sekali lagi kami membungkus fungsi baru kami dalam penutupan.
def get_log_lik_transformed(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_transformed(transformed_precisions):
return (log_lik_data_transformed(transformed_precisions, replicated_data) +
log_lik_prior_transformed(transformed_precisions))
return _log_lik_transformed
# make sure everything runs
log_lik_fn = get_log_lik_transformed(my_data)
m = tf.eye(2)[tf.newaxis, ...]
lik = log_lik_fn(precision_to_unconstrained.forward(m)).numpy()
print(lik)
[-431.5611]
Contoh
Sekarang kita tidak perlu khawatir tentang sampler kita yang meledak karena nilai parameter yang tidak valid, mari kita buat beberapa sampel nyata.
Sampler bekerja dengan versi parameter kita yang tidak dibatasi, jadi kita perlu mengubah nilai awal kita ke versi yang tidak dibatasi. Sampel yang kami hasilkan juga semuanya dalam bentuk yang tidak dibatasi, jadi kami perlu mengubahnya kembali. Bijector divektorkan, jadi mudah untuk melakukannya.
# We'll choose a proper random initial value this time
np.random.seed(123)
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_value = initial_value_cholesky.dot(
initial_value_cholesky.T)[np.newaxis, ...]
# The sampler works with unconstrained values, so we'll transform our initial
# value
initial_value_transformed = precision_to_unconstrained.forward(
initial_value).numpy()
# Sample!
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data, n_chains=1)
num_results = 1000
num_burnin_steps = 1000
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
initial_value_transformed,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=lambda _, pkr: pkr.is_accepted,
seed=123)
# transform samples back to their constrained form
precision_samples = [precision_to_unconstrained.inverse(s) for s in states]
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
Mari kita bandingkan rata-rata keluaran sampler kita dengan rata-rata posterior analitik!
print('True posterior mean:\n', posterior_mean)
print('Sample mean:\n', np.mean(np.reshape(precision_samples, [-1, 2, 2]), axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Sample mean: [[ 1.4315274 -0.25587553] [-0.25587553 0.5740424 ]]
Kami jauh! Mari kita cari tahu alasannya. Pertama mari kita lihat sampel kami.
np.reshape(precision_samples, [-1, 2, 2])
array([[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
...,
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]]], dtype=float32)
Uh oh - sepertinya mereka semua memiliki nilai yang sama. Mari kita cari tahu alasannya.
The kernel_results_ variabel adalah tupel bernama yang memberikan informasi tentang sampler di masing-masing negara. The is_accepted lapangan adalah kunci di sini.
# Look at the acceptance for the last 100 samples
print(np.squeeze(is_accepted)[-100:])
print('Fraction of samples accepted:', np.mean(np.squeeze(is_accepted)))
[False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False] Fraction of samples accepted: 0.0
Semua sampel kami ditolak! Agaknya ukuran langkah kami terlalu besar. Saya memilih stepsize=0.1 murni sewenang-wenang.
Versi 3: pengambilan sampel dengan ukuran langkah adaptif
Karena pengambilan sampel dengan pilihan ukuran langkah saya yang sewenang-wenang gagal, kami memiliki beberapa item agenda:
- menerapkan ukuran langkah adaptif, dan
- melakukan beberapa pemeriksaan konvergensi.
Ada beberapa contoh kode yang bagus di tensorflow_probability/python/mcmc/hmc.py untuk melaksanakan ukuran langkah adaptif. Saya telah mengadaptasinya di bawah.
Perhatikan bahwa ada yang terpisah sess.run() pernyataan untuk setiap langkah. Ini sangat membantu untuk debugging, karena memungkinkan kita untuk dengan mudah menambahkan beberapa diagnostik per langkah jika perlu. Misalnya, kami dapat menunjukkan kemajuan tambahan, waktu setiap langkah, dll.
Tip: Salah satu cara tampaknya umum untuk mengacaukan sampling Anda adalah memiliki grafik tumbuh Anda dalam lingkaran. (Alasan untuk menyelesaikan grafik sebelum sesi dijalankan adalah untuk mencegah masalah seperti itu.) Namun, jika Anda belum pernah menggunakan finalize(), pemeriksaan debug yang berguna jika kode Anda melambat hingga perayapan adalah dengan mencetak grafik ukuran pada setiap langkah melalui len(mygraph.get_operations()) - jika panjang meningkat, Anda mungkin melakukan sesuatu yang buruk.
Kami akan menjalankan 3 rantai independen di sini. Melakukan beberapa perbandingan antara rantai akan membantu kami memeriksa konvergensi.
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values = []
for i in range(N_CHAINS):
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_values.append(initial_value_cholesky.dot(initial_value_cholesky.T))
initial_values = np.stack(initial_values)
initial_values_transformed = precision_to_unconstrained.forward(
initial_values).numpy()
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=hmc,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values_transformed,
kernel=adapted_kernel,
trace_fn=lambda _, pkr: pkr.inner_results.is_accepted,
parallel_iterations=1)
# transform samples back to their constrained form
precision_samples = precision_to_unconstrained.inverse(states)
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
Pemeriksaan cepat: tingkat penerimaan kami selama pengambilan sampel kami mendekati target kami di 0,651.
print(np.mean(is_accepted))
0.6190666666666667
Lebih baik lagi, rata-rata sampel dan simpangan baku kami mendekati apa yang kami harapkan dari solusi analitik.
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96426415 -1.6519215 ] [-1.6519215 3.8614824 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13622096 0.25235635] [0.25235635 0.5394968 ]]
Memeriksa konvergensi
Secara umum kami tidak akan memiliki solusi analitik untuk diperiksa, jadi kami harus memastikan sampler telah konvergen. Satu cek standar adalah Gelman-Rubin \(\hat{R}\) statistik, yang memerlukan beberapa rantai sampling. \(\hat{R}\) langkah-langkah sejauh mana varians (sarana) antara rantai melebihi apa yang diharapkan jika rantai yang terdistribusi secara identik. Nilai-nilai \(\hat{R}\) dekat dengan 1 digunakan untuk menunjukkan konvergensi perkiraan. Lihat sumber untuk rincian.
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0038308 1.0005717] [1.0005717 1.0006068]]
Kritik model
Jika kita tidak memiliki solusi analitik, inilah saatnya untuk melakukan beberapa kritik model nyata.
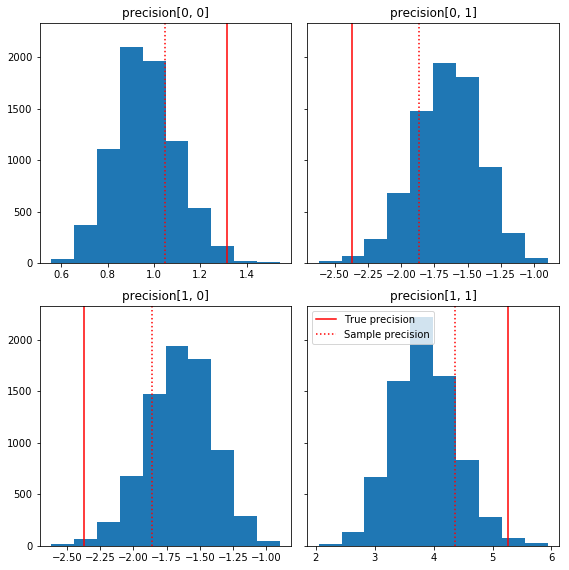
Berikut adalah beberapa histogram cepat dari komponen sampel relatif terhadap kebenaran dasar kami (berwarna merah). Perhatikan bahwa sampel telah menyusut dari nilai matriks presisi sampel menuju matriks identitas sebelumnya.
fig, axes = plt.subplots(2, 2, sharey=True)
fig.set_size_inches(8, 8)
for i in range(2):
for j in range(2):
ax = axes[i, j]
ax.hist(precision_samples_reshaped[:, i, j])
ax.axvline(true_precision[i, j], color='red',
label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':',
label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.tight_layout()
plt.legend()
plt.show()
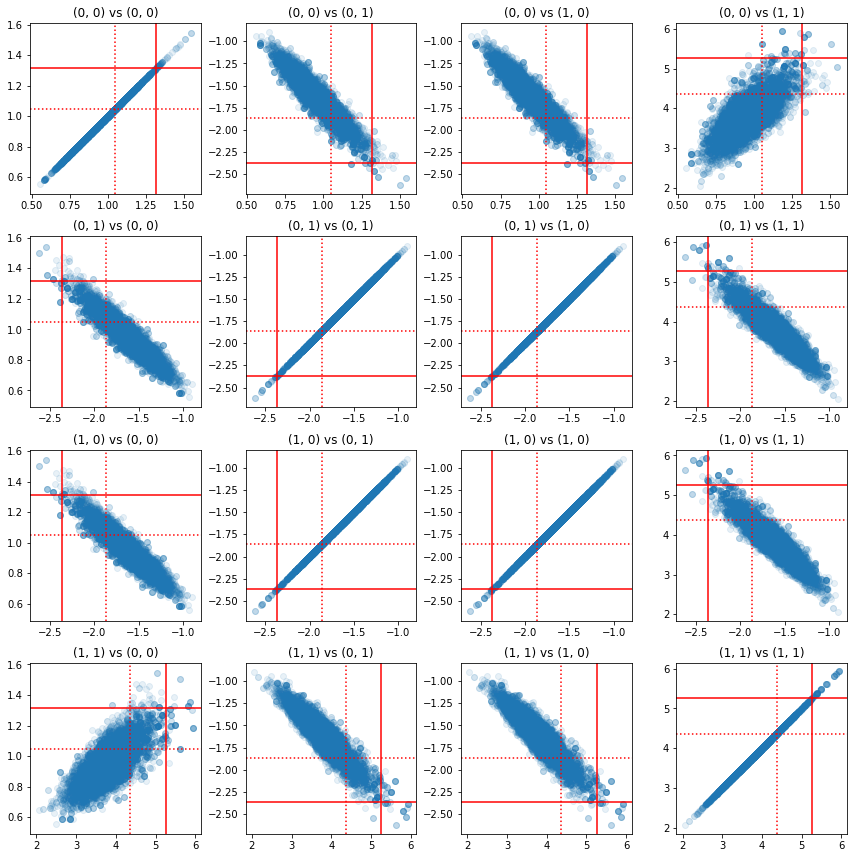
Beberapa scatterplot dari pasangan komponen presisi menunjukkan bahwa karena struktur korelasi dari posterior, nilai posterior yang sebenarnya tidak seperti yang terlihat dari marginal di atas.
fig, axes = plt.subplots(4, 4)
fig.set_size_inches(12, 12)
for i1 in range(2):
for j1 in range(2):
index1 = 2 * i1 + j1
for i2 in range(2):
for j2 in range(2):
index2 = 2 * i2 + j2
ax = axes[index1, index2]
ax.scatter(precision_samples_reshaped[:, i1, j1],
precision_samples_reshaped[:, i2, j2], alpha=0.1)
ax.axvline(true_precision[i1, j1], color='red')
ax.axhline(true_precision[i2, j2], color='red')
ax.axvline(sample_precision[i1, j1], color='red', linestyle=':')
ax.axhline(sample_precision[i2, j2], color='red', linestyle=':')
ax.set_title('(%d, %d) vs (%d, %d)' % (i1, j1, i2, j2))
plt.tight_layout()
plt.show()
Versi 4: pengambilan sampel parameter terbatas yang lebih sederhana
Bijector membuat pengambilan sampel matriks presisi menjadi mudah, tetapi ada cukup banyak konversi manual ke dan dari representasi yang tidak dibatasi. Ada cara yang lebih mudah!
Kernel Transisi yang Diubah
The TransformedTransitionKernel menyederhanakan proses ini. Ini membungkus sampler Anda dan menangani semua konversi. Dibutuhkan sebagai argumen daftar bijector yang memetakan nilai parameter yang tidak dibatasi ke yang dibatasi. Jadi di sini kita perlu kebalikan dari precision_to_unconstrained bijector kita gunakan di atas. Kami hanya bisa menggunakan tfb.Invert(precision_to_unconstrained) , tapi itu akan melibatkan mengambil invers dari invers (TensorFlow tidak cukup pintar untuk menyederhanakan tf.Invert(tf.Invert()) ke tf.Identity()) , jadi bukan kami 'hanya akan menulis bijector baru.
Bijektor pembatas
# The bijector we need for the TransformedTransitionKernel is the inverse of
# the one we used above
unconstrained_to_precision = tfb.Chain([
# step 3: take the product of Cholesky factors
tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS),
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: map a vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# quick sanity check
m = [[1., 2.], [2., 8.]]
m_inv = unconstrained_to_precision.inverse(m).numpy()
m_fwd = unconstrained_to_precision.forward(m_inv).numpy()
print('m:\n', m)
print('unconstrained_to_precision.inverse(m):\n', m_inv)
print('forward(unconstrained_to_precision.inverse(m)):\n', m_fwd)
m: [[1.0, 2.0], [2.0, 8.0]] unconstrained_to_precision.inverse(m): [0.6931472 2. 0. ] forward(unconstrained_to_precision.inverse(m)): [[1. 2.] [2. 8.]]
Pengambilan sampel dengan TransformedTransitionKernel
Dengan TransformedTransitionKernel , kita tidak lagi harus melakukan transformasi manual parameter kami. Nilai awal dan sampel kami semuanya adalah matriks presisi; kita hanya perlu meneruskan bijector tanpa batasan kita ke kernel dan itu menangani semua transformasi.
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
return states
precision_samples = sample()
Memeriksa konvergensi
The \(\hat{R}\) konvergensi cek penampilan yang baik!
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013582 1.0019467] [1.0019467 1.0011805]]
Perbandingan dengan posterior analitik
Sekali lagi mari kita periksa terhadap posterior analitik.
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96687526 -1.6552585 ] [-1.6552585 3.867676 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329624 0.24913791] [0.24913791 0.53983927]]
Optimasi
Sekarang setelah semuanya berjalan dari ujung ke ujung, mari lakukan versi yang lebih optimal. Kecepatan tidak terlalu menjadi masalah untuk contoh ini, tetapi begitu matriks menjadi lebih besar, beberapa pengoptimalan akan membuat perbedaan besar.
Salah satu peningkatan kecepatan besar yang dapat kita lakukan adalah melakukan parameterisasi ulang dalam hal dekomposisi Cholesky. Alasannya adalah fungsi kemungkinan data kami membutuhkan matriks kovarians dan presisi. Matrix inversi mahal (\(O(n^3)\) untuk \(n \times n\) matrix), dan jika kita parameterisasi dari segi baik kovarians atau matriks presisi, perlu kita lakukan inversi untuk mendapatkan yang lain.
Sebagai pengingat, nyata, positif-pasti, matriks simetris \(M\) dapat didekomposisi menjadi produk dari bentuk \(M = L L^T\) mana matriks \(L\) adalah segitiga bawah dan memiliki diagonal positif. Mengingat Cholesky dekomposisi \(M\), kita dapat lebih efisien memperoleh baik \(M\) (produk dari bawah dan matriks segitiga atas) dan \(M^{-1}\) (melalui substitusi). Faktorisasi Cholesky sendiri tidak murah untuk dihitung, tetapi jika kita membuat parameter dalam hal faktor Cholesky, kita hanya perlu menghitung faktorisasi Choleksy dari nilai parameter awal.
Menggunakan dekomposisi Cholesky dari matriks kovarians
TFP memiliki versi dari distribusi normal multivariat, MultivariateNormalTriL , yang parameterized dalam hal faktor Cholesky dari matriks kovarians. Jadi jika kita membuat parameter dalam hal faktor Cholesky dari matriks kovarians, kita dapat menghitung kemungkinan log data secara efisien. Tantangannya adalah dalam menghitung kemungkinan log sebelumnya dengan efisiensi yang sama.
Jika kami memiliki versi distribusi Wishart terbalik yang bekerja dengan faktor sampel Cholesky, kami akan siap. Sayangnya, kita tidak. (Namun, tim akan menyambut pengiriman kode!) Sebagai alternatif, kita dapat menggunakan versi distribusi Wishart yang bekerja dengan faktor sampel Cholesky bersama dengan rantai bijektor.
Saat ini, kami kehilangan beberapa bijector stok untuk membuat segalanya menjadi sangat efisien, tetapi saya ingin menunjukkan prosesnya sebagai latihan dan ilustrasi yang berguna tentang kekuatan bijector TFP.
Distribusi Wishart yang beroperasi pada faktor Cholesky
The Wishart distribusi memiliki bendera yang berguna, input_output_cholesky , yang menentukan bahwa input dan output matriks harus faktor Cholesky. Lebih efisien dan menguntungkan secara numerik untuk bekerja dengan faktor Cholesky daripada matriks penuh, itulah sebabnya ini diinginkan. Poin penting tentang semantik bendera: itu hanya merupakan indikasi bahwa representasi dari input dan output untuk distribusi harus mengubah - itu tidak menunjukkan reparameterization penuh distribusi, yang akan melibatkan koreksi Jacobian ke log_prob() fungsi. Kami sebenarnya ingin melakukan reparameterisasi penuh ini, jadi kami akan membangun distribusi kami sendiri.
# An optimized Wishart distribution that has been transformed to operate on
# Cholesky factors instead of full matrices. Note that we gain a modest
# additional speedup by specifying the Cholesky factor of the scale matrix
# (i.e. by passing in the scale_tril parameter instead of scale).
class CholeskyWishart(tfd.TransformedDistribution):
"""Wishart distribution reparameterized to use Cholesky factors."""
def __init__(self,
df,
scale_tril,
validate_args=False,
allow_nan_stats=True,
name='CholeskyWishart'):
# Wishart has a bunch of methods that we want to support but not
# implement. We'll subclass TransformedDistribution here to take care of
# those. We'll override the few for which speed is critical and implement
# them with a separate Wishart for which input_output_cholesky=True
super(CholeskyWishart, self).__init__(
distribution=tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=False,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()),
validate_args=validate_args,
name=name
)
# Here's the Cholesky distribution we'll use for log_prob() and sample()
self.cholesky = tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=True,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats)
def _log_prob(self, x):
return (self.cholesky.log_prob(x) +
self.bijector.inverse_log_det_jacobian(x, event_ndims=2))
def _sample_n(self, n, seed=None):
return self.cholesky._sample_n(n, seed)
# some checks
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
@tf.function(autograph=False)
def compute_log_prob(m):
w_transformed = tfd.TransformedDistribution(
tfd.WishartTriL(df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()))
w_optimized = CholeskyWishart(
df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY)
log_prob_transformed = w_transformed.log_prob(m)
log_prob_optimized = w_optimized.log_prob(m)
return log_prob_transformed, log_prob_optimized
for matrix in [np.eye(2, dtype=np.float32),
np.array([[1., 0.], [2., 8.]], dtype=np.float32)]:
log_prob_transformed, log_prob_optimized = [
t.numpy() for t in compute_log_prob(matrix)]
print('Transformed Wishart:', log_prob_transformed)
print('Optimized Wishart', log_prob_optimized)
Transformed Wishart: -0.84889317 Optimized Wishart -0.84889317 Transformed Wishart: -99.269455 Optimized Wishart -99.269455
Membangun distribusi Wishart terbalik
Kami memiliki kami kovarians matriks \(C\) didekomposisi menjadi \(C = L L^T\) mana \(L\) adalah segitiga bawah dan memiliki diagonal positif. Kami ingin tahu kemungkinan \(L\) mengingat bahwa \(C \sim W^{-1}(\nu, V)\) mana \(W^{-1}\) adalah kebalikan distribusi Wishart.
Kebalikan distribusi Wishart memiliki properti bahwa jika \(C \sim W^{-1}(\nu, V)\), maka matriks presisi \(C^{-1} \sim W(\nu, V^{-1})\). Jadi kita bisa mendapatkan probabilitas \(L\) melalui TransformedDistribution yang mengambil sebagai parameter distribusi Wishart dan bijector yang memetakan faktor Cholesky matriks presisi untuk faktor Cholesky dari kebalikannya.
Sebuah cara sederhana (tapi tidak super efisien) untuk mendapatkan dari faktor Cholesky dari \(C^{-1}\) ke \(L\) adalah untuk membalikkan faktor Cholesky oleh kembali pemecahan, maka membentuk matriks kovarians dari faktor-faktor terbalik, dan kemudian melakukan faktorisasi Cholesky .
Biarkan Cholesky dekomposisi \(C^{-1} = M M^T\). \(M\) adalah segitiga bawah, sehingga kami dapat membalikkan itu menggunakan MatrixInverseTriL bijector.
Membentuk \(C\) dari \(M^{-1}\) adalah sedikit rumit: \(C = (M M^T)^{-1} = M^{-T}M^{-1} = M^{-T} (M^{-T})^T\). \(M\) adalah segitiga bawah, sehingga \(M^{-1}\) juga akan segitiga bawah, dan \(M^{-T}\) akan segitiga atas. The CholeskyOuterProduct() bijector hanya bekerja dengan matriks segitiga bawah, sehingga kita tidak dapat menggunakannya untuk membentuk \(C\) dari \(M^{-T}\). Solusi kami adalah rantai bijektor yang mengubah baris dan kolom matriks.
Untungnya logika ini dirumuskan dalam CholeskyToInvCholesky bijector!
Menggabungkan semua bagian
# verify that the bijector works
m = np.array([[1., 0.], [2., 8.]], dtype=np.float32)
c_inv = m.dot(m.T)
c = np.linalg.inv(c_inv)
c_chol = np.linalg.cholesky(c)
wishart_cholesky_to_iw_cholesky = tfb.CholeskyToInvCholesky()
w_fwd = wishart_cholesky_to_iw_cholesky.forward(m).numpy()
print('numpy =\n', c_chol)
print('bijector =\n', w_fwd)
numpy = [[ 1.0307764 0. ] [-0.03031695 0.12126781]] bijector = [[ 1.0307764 0. ] [-0.03031695 0.12126781]]
Distribusi akhir kami
Wishart terbalik kami yang beroperasi pada faktor Cholesky adalah sebagai berikut:
inverse_wishart_cholesky = tfd.TransformedDistribution(
distribution=CholeskyWishart(
df=PRIOR_DF,
scale_tril=np.linalg.cholesky(np.linalg.inv(PRIOR_SCALE))),
bijector=tfb.CholeskyToInvCholesky())
Kita memiliki invers Wishart, tapi agak lambat karena kita harus melakukan dekomposisi Cholesky di bijector. Mari kembali ke parameterisasi matriks presisi dan lihat apa yang bisa kita lakukan di sana untuk optimasi.
Final(!) Version: menggunakan dekomposisi Cholesky dari matriks presisi
Pendekatan alternatif adalah bekerja dengan faktor Cholesky dari matriks presisi. Di sini fungsi kemungkinan sebelumnya mudah dihitung, tetapi fungsi kemungkinan log data membutuhkan lebih banyak pekerjaan karena TFP tidak memiliki versi normal multivariat yang diparameterisasi oleh presisi.
Kemungkinan log sebelumnya yang dioptimalkan
Kami menggunakan CholeskyWishart distribusi kami membangun di atas untuk membangun sebelumnya.
# Our new prior.
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
def log_lik_prior_cholesky(precisions_cholesky):
rv_precision = CholeskyWishart(
df=PRIOR_DF,
scale_tril=PRIOR_SCALE_CHOLESKY,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions_cholesky)
# Check against the slower TF implementation and the NumPy implementation.
# Note that when comparing to NumPy, we need to add in the Jacobian correction.
precisions = [np.eye(2, dtype=np.float32),
true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
lik_tf = log_lik_prior_cholesky(precisions_cholesky).numpy()
lik_tf_slow = tfd.TransformedDistribution(
distribution=tfd.WishartTriL(
df=PRIOR_DF, scale_tril=tf.linalg.cholesky(PRIOR_SCALE)),
bijector=tfb.Invert(tfb.CholeskyOuterProduct())).log_prob(
precisions_cholesky).numpy()
corrections = tfb.Invert(tfb.CholeskyOuterProduct()).inverse_log_det_jacobian(
precisions_cholesky, event_ndims=2).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow slow:', lik_tf_slow[i])
print('tensorflow fast:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow slow: -0.84889317 tensorflow fast: -0.84889317 1 numpy: -7.442875031036973 tensorflow slow: -7.442877 tensorflow fast: -7.442876
Kemungkinan log data yang dioptimalkan
We can use TFP's bijectors to build our own version of the multivariate normal. Here is the key idea:
Suppose I have a column vector \(X\) whose elements are iid samples of \(N(0, 1)\). We have \(\text{mean}(X) = 0\) and \(\text{cov}(X) = I\)
Now let \(Y = A X + b\). We have \(\text{mean}(Y) = b\) and \(\text{cov}(Y) = A A^T\)
Hence we can make vectors with mean \(b\) and covariance \(C\) using the affine transform \(Ax+b\) to vectors of iid standard Normal samples provided \(A A^T = C\). The Cholesky decomposition of \(C\) has the desired property. However, there are other solutions.
Let \(P = C^{-1}\) and let the Cholesky decomposition of \(P\) be \(B\), ie \(B B^T = P\). Now
\(P^{-1} = (B B^T)^{-1} = B^{-T} B^{-1} = B^{-T} (B^{-T})^T\)
So another way to get our desired mean and covariance is to use the affine transform \(Y=B^{-T}X + b\).
Our approach (courtesy of this notebook ):
- Use
tfd.Independent()to combine a batch of 1-DNormalrandom variables into a single multi-dimensional random variable. Thereinterpreted_batch_ndimsparameter forIndependent()specifies the number of batch dimensions that should be reinterpreted as event dimensions. In our case we create a 1-D batch of length 2 that we transform into a 1-D event of length 2, soreinterpreted_batch_ndims=1. - Apply a bijector to add the desired covariance:
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky, adjoint=True)). Note that above we're multiplying our iid normal random variables by the transpose of the inverse of the Cholesky factor of the precision matrix \((B^{-T}X)\). Thetfb.Inverttakes care of inverting \(B\), and theadjoint=Trueflag performs the transpose. - Apply a bijector to add the desired offset:
tfb.Shift(shift=shift)Note that we have to do the shift as a separate step from the initial inverted affine transform because otherwise the inverted scale is applied to the shift (since the inverse of \(y=Ax+b\) is \(x=A^{-1}y - A^{-1}b\)).
class MVNPrecisionCholesky(tfd.TransformedDistribution):
"""Multivariate normal parameterized by loc and Cholesky precision matrix."""
def __init__(self, loc, precision_cholesky, name=None):
super(MVNPrecisionCholesky, self).__init__(
distribution=tfd.Independent(
tfd.Normal(loc=tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky,
adjoint=True)),
]),
name=name)
@tf.function(autograph=False)
def log_lik_data_cholesky(precisions_cholesky, replicated_data):
n = tf.shape(precisions_cholesky)[0] # number of precision matrices
rv_data = MVNPrecisionCholesky(
loc=tf.zeros([n, 2]),
precision_cholesky=precisions_cholesky)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# check against the numpy implementation
true_precision_cholesky = np.linalg.cholesky(true_precision)
precisions = [np.eye(2, dtype=np.float32), true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
n = precisions_cholesky.shape[0]
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
lik_tf = log_lik_data_cholesky(precisions_cholesky, replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.81824
Combined log likelihood function
Now we combine our prior and data log likelihood functions in a closure.
def get_log_lik_cholesky(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_cholesky(precisions_cholesky):
return (log_lik_data_cholesky(precisions_cholesky, replicated_data) +
log_lik_prior_cholesky(precisions_cholesky))
return _log_lik_cholesky
Constraining bijector
Our samples are constrained to be valid Cholesky factors, which means they must be lower triangular matrices with positive diagonals. The TransformedTransitionKernel needs a bijector that maps unconstrained tensors to/from tensors with our desired constraints. We've removed the Cholesky decomposition from the bijector's inverse, which speeds things up.
unconstrained_to_precision_cholesky = tfb.Chain([
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: expand the vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# some checks
inv = unconstrained_to_precision_cholesky.inverse(precisions_cholesky).numpy()
fwd = unconstrained_to_precision_cholesky.forward(inv).numpy()
print('precisions_cholesky:\n', precisions_cholesky)
print('\ninv:\n', inv)
print('\nfwd(inv):\n', fwd)
precisions_cholesky: [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]] inv: [[ 0.0000000e+00 0.0000000e+00 0.0000000e+00] [ 3.5762781e-07 -2.0647411e+00 1.3721828e-01]] fwd(inv): [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]]
Initial values
We generate a tensor of initial values. We're working with Cholesky factors, so we generate some Cholesky factor initial values.
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values_cholesky = []
for i in range(N_CHAINS):
initial_values_cholesky.append(np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32))
initial_values_cholesky = np.stack(initial_values_cholesky)
Sampling
We sample N_CHAINS chains using the TransformedTransitionKernel .
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_cholesky(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision_cholesky)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
samples = tf.linalg.matmul(states, states, transpose_b=True)
return samples
precision_samples = sample()
Convergence check
A quick convergence check looks good:
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013583 1.0019467] [1.0019467 1.0011804]]
Comparing results to the analytic posterior
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, newshape=[-1, 2, 2])
And again, the sample means and standard deviations match those of the analytic posterior.
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.9668749 -1.6552604] [-1.6552604 3.8676758]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329637 0.24913797] [0.24913797 0.53983945]]
Ok, all done! We've got our optimized sampler working.
