Conozca lo último en aprendizaje automático, IA generativa y más en el Simposio WiML 2023.

Se usó la API de Cloud Translation para traducir esta página.

Estudio de caso de probabilidad de TensorFlow: estimación de covarianza

Ver en TensorFlow.org

Ejecutar en Google Colab

Ver fuente en GitHub

Descargar cuaderno

Escribí este cuaderno como un caso de estudio para aprender TensorFlow Probability. El problema que elegí resolver es estimar una matriz de covarianza para muestras de una variable aleatoria gaussiana media 0 de 2-D. El problema tiene un par de características interesantes:

Si usamos un Wishart previo inverso para la covarianza (un enfoque común), el problema tiene una solución analítica, por lo que podemos verificar nuestros resultados.
El problema implica el muestreo de un parámetro restringido, lo que agrega cierta complejidad interesante.
La solución más sencilla no es la más rápida, por lo que hay trabajo de optimización por hacer.

Decidí escribir mis experiencias sobre la marcha. Me tomó un tiempo comprender los puntos más finos de TFP, por lo que este portátil comienza de manera bastante simple y luego gradualmente trabaja con funciones de TFP más complicadas. Me encontré con muchos problemas en el camino y traté de capturar tanto los procesos que me ayudaron a identificarlos como las soluciones que finalmente encontré. He tratado de incluir un montón de detalles (incluyendo un montón de pruebas para asegurarse de pasos individuales son correctos).

¿Por qué aprender TensorFlow Probability?

Encontré TensorFlow Probability atractivo para mi proyecto por algunas razones:

La probabilidad de TensorFlow le permite desarrollar prototipos de modelos complejos de forma interactiva en una computadora portátil. Puede dividir su código en partes pequeñas que puede probar de forma interactiva y con pruebas unitarias.
Una vez que esté listo para escalar, puede aprovechar toda la infraestructura que tenemos para hacer que TensorFlow se ejecute en múltiples procesadores optimizados en múltiples máquinas.
Finalmente, aunque me gusta mucho Stan, me resulta bastante difícil depurarlo. Tienes que escribir todo tu código de modelado en un lenguaje autónomo que tiene muy pocas herramientas que te permitan pinchar tu código, inspeccionar estados intermedios, etc.

La desventaja es que TensorFlow Probability es mucho más nuevo que Stan y PyMC3, por lo que la documentación es un trabajo en progreso y hay muchas funciones que aún no se han creado. Afortunadamente, encontré que la base de TFP es sólida y está diseñada de una manera modular que permite extender su funcionalidad de manera bastante sencilla. En este cuaderno, además de resolver el caso de estudio, mostraré algunas formas de ampliar la TFP.

Para quien es esto

Supongo que los lectores llegan a este cuaderno con algunos requisitos previos importantes. Debería:

Conozca los conceptos básicos de la inferencia bayesiana. (Si no lo hace, un muy buen primer libro es Rethinking estadístico )
Tener cierta familiaridad con una biblioteca de muestreo MCMC, por ejemplo Stan / PyMC3 / FALLOS
Tener una comprensión sólida de NumPy (Una introducción buena es Python para Análisis de Datos )
Tener al menos cierta familiaridad con TensorFlow , pero no necesariamente experiencia. ( Aprendizaje TensorFlow es bueno, pero la rápida evolución de los medios TensorFlow que la mayoría de los libros será un poco anticuado. De Stanford CS20 supuesto también es bueno.)

Primer intento

Este es mi primer intento con el problema. Spoiler: mi solución no funciona, ¡y serán necesarios varios intentos para hacer las cosas bien! Aunque el proceso lleva un tiempo, cada intento a continuación ha sido útil para aprender una nueva parte de la PTF.

Una nota: TFP no implementa actualmente la distribución inversa de Wishart (veremos al final cómo rodar nuestro propio Wishart inverso), así que en cambio cambiaré el problema al de estimar una matriz de precisión usando un Wishart a priori.

import collections
import math
import os
import time

import numpy as np
import pandas as pd
import scipy
import scipy.stats
import matplotlib.pyplot as plt

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors

Paso 1: reúna las observaciones

Mis datos aquí son todos sintéticos, por lo que esto parecerá un poco más ordenado que un ejemplo del mundo real. Sin embargo, no hay ninguna razón por la que no pueda generar algunos datos sintéticos por su cuenta.

Consejo: Una vez que haya decidido sobre la forma de su modelo, se puede recoger algunos valores de los parámetros y utilizar el modelo elegido para generar algunos datos sintéticos. Como comprobación de la cordura de su implementación, puede verificar que sus estimaciones incluyan los valores reales de los parámetros que eligió. Para acelerar su ciclo de depuración / prueba, puede considerar una versión simplificada de su modelo (por ejemplo, use menos dimensiones o menos muestras).

Consejo: Es más fácil trabajar con sus observaciones como matrices NumPy. Una cosa importante a tener en cuenta es que NumPy por defecto usa float64, mientras que TensorFlow por defecto usa float32.

En general, las operaciones de TensorFlow quieren que todos los argumentos tengan el mismo tipo, y debes realizar una transmisión de datos explícita para cambiar los tipos. Si usa observaciones float64, necesitará agregar muchas operaciones de conversión. NumPy, por el contrario, se encargará del lanzamiento automáticamente. Por lo tanto, es mucho más fácil de convertir sus datos en numpy float32 de lo que es para obligar a TensorFlow uso float64.

Elija algunos valores de parámetro

# We're assuming 2-D data with a known true mean of (0, 0)
true_mean = np.zeros([2], dtype=np.float32)
# We'll make the 2 coordinates correlated
true_cor = np.array([[1.0, 0.9], [0.9, 1.0]], dtype=np.float32)
# And we'll give the 2 coordinates different variances
true_var = np.array([4.0, 1.0], dtype=np.float32)
# Combine the variances and correlations into a covariance matrix
true_cov = np.expand_dims(np.sqrt(true_var), axis=1).dot(
    np.expand_dims(np.sqrt(true_var), axis=1).T) * true_cor
# We'll be working with precision matrices, so we'll go ahead and compute the
# true precision matrix here
true_precision = np.linalg.inv(true_cov)

# Here's our resulting covariance matrix
print(true_cov)
# Verify that it's positive definite, since np.random.multivariate_normal
# complains about it not being positive definite for some reason.
# (Note that I'll be including a lot of sanity checking code in this notebook -
# it's a *huge* help for debugging)
print('eigenvalues: ', np.linalg.eigvals(true_cov))

[[4.  1.8]
 [1.8 1. ]]
eigenvalues:  [4.843075   0.15692513]

Genera algunas observaciones sintéticas

Tenga en cuenta que TensorFlow Probabilidad utiliza la convención de que la dimensión inicial (s) de sus datos representan índices de la muestra, y la dimensión final (s) de sus datos representan la dimensionalidad de sus muestras.

Aquí queremos 100 muestras, cada una de las cuales es un vector de longitud 2. Vamos a generar una matriz my_data con forma (100, 2). my_data[i, :] es la \(i\)ésima muestra, y es un vector de longitud 2.

(Recuerde hacer my_data tener float32 tipo!)

# Set the seed so the results are reproducible.
np.random.seed(123)

# Now generate some observations of our random variable.
# (Note that I'm suppressing a bunch of spurious about the covariance matrix
# not being positive semidefinite via check_valid='ignore' because it really is
# positive definite!)
my_data = np.random.multivariate_normal(
    mean=true_mean, cov=true_cov, size=100,
    check_valid='ignore').astype(np.float32)

my_data.shape

(100, 2)

Cordura comprobar las observaciones

¡Una fuente potencial de errores es estropear sus datos sintéticos! Hagamos algunas comprobaciones sencillas.

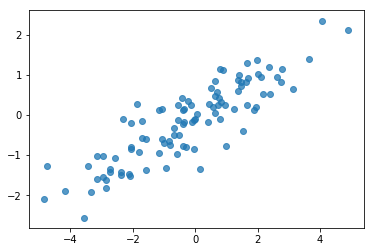
# Do a scatter plot of the observations to make sure they look like what we
# expect (higher variance on the x-axis, y values strongly correlated with x)
plt.scatter(my_data[:, 0], my_data[:, 1], alpha=0.75)
plt.show()

png

print('mean of observations:', np.mean(my_data, axis=0))
print('true mean:', true_mean)

mean of observations: [-0.24009615 -0.16638893]
true mean: [0. 0.]

print('covariance of observations:\n', np.cov(my_data, rowvar=False))
print('true covariance:\n', true_cov)

covariance of observations:
 [[3.95307734 1.68718486]
 [1.68718486 0.94910269]]
true covariance:
 [[4.  1.8]
 [1.8 1. ]]

Ok, nuestras muestras parecen razonables. Próximo paso.

Paso 2: implementar la función de probabilidad en NumPy

Lo principal que necesitaremos escribir para realizar nuestro muestreo MCMC en TF Probability es una función de probabilidad logarítmica. En general, es un poco más complicado escribir TF que NumPy, por lo que me resulta útil hacer una implementación inicial en NumPy. Voy a dividir la función de verosimilitud en 2 piezas, una función de verosimilitud de datos que corresponde a \(P(data | parameters)\) y una función de probabilidad antes de que corresponde a \(P(parameters)\).

Tenga en cuenta que estas funciones de NumPy no tienen que estar súper optimizadas / vectorizadas ya que el objetivo es solo generar algunos valores para las pruebas. ¡La corrección es la consideración clave!

Primero implementaremos la pieza de probabilidad del registro de datos. Eso es bastante sencillo. Lo único que debemos recordar es que vamos a trabajar con matrices de precisión, así que parametrizaremos en consecuencia.

def log_lik_data_numpy(precision, data):
  # np.linalg.inv is a really inefficient way to get the covariance matrix, but
  # remember we don't care about speed here
  cov = np.linalg.inv(precision)
  rv = scipy.stats.multivariate_normal(true_mean, cov)
  return np.sum(rv.logpdf(data))

# test case: compute the log likelihood of the data given the true parameters
log_lik_data_numpy(true_precision, my_data)

-280.81822950593767

Vamos a utilizar un Wishart previa para la matriz de precisión ya que no hay una solución analítica para la parte posterior (ver tabla útil de Wikipedia de priores conjugadas ).

La distribución de Wishart tiene 2 parámetros:

el número de grados de libertad (con la etiqueta \(\nu\) en Wikipedia)
una matriz de escala (etiquetado \(V\) en Wikipedia)

La media para una distribución de Wishart con parámetros \(\nu, V\) es \(E[W] = \nu V\), y la varianza es \(\text{Var}(W_{ij}) = \nu(v_{ij}^2+v_{ii}v_{jj})\)

Algunos intuición útil: Puede generar una muestra mediante la generación de Wishart \(\nu\) independiente dibuja \(x_1 \ldots x_{\nu}\) de una variable aleatoria normal multivariante con media 0 y covarianza \(V\) y luego la formación de la suma \(W = \sum_{i=1}^{\nu} x_i x_i^T\).

Si RESCALE muestras Wishart dividiéndolos por \(\nu\), se obtiene la matriz de covarianza de la muestra de la \(x_i\). Esta matriz de covarianza de la muestra debe tender hacia \(V\) como \(\nu\) aumenta. Cuando \(\nu\) es pequeña, hay un montón de variación en la matriz de covarianza de la muestra, los valores tan pequeños de \(\nu\) corresponden a priors más débiles y valores grandes de \(\nu\) corresponden a priors fuertes. Tenga en cuenta que \(\nu\) deben ser al menos tan grande como la dimensión del espacio Te muestreo o va a generar matrices singulares.

Vamos a utilizar \(\nu = 3\) así que tenemos una débil antes, y vamos a tener \(V = \frac{1}{\nu} I\) que tiran de nuestra estimación de covarianza hacia la identidad (recordemos que la media es \(\nu V\)).

PRIOR_DF = 3
PRIOR_SCALE = np.eye(2, dtype=np.float32) / PRIOR_DF

def log_lik_prior_numpy(precision):
  rv = scipy.stats.wishart(df=PRIOR_DF, scale=PRIOR_SCALE)
  return rv.logpdf(precision)

# test case: compute the prior for the true parameters
log_lik_prior_numpy(true_precision)

-9.103606346649766

La distribución de Wishart es el conjugado anterior para estimar la matriz de precisión de una normal multivariante con media conocida \(\mu\).

Supongamos que los parámetros anteriores son Wishart \(\nu, V\) y que tenemos \(n\) observaciones de nuestro multivariante, la normalidad \(x_1, \ldots, x_n\). Los parámetros posteriores son \(n + \nu, \left(V^{-1} + \sum_{i=1}^n (x_i-\mu)(x_i-\mu)^T \right)^{-1}\).

n = my_data.shape[0]
nu_prior = PRIOR_DF
v_prior = PRIOR_SCALE
nu_posterior = nu_prior + n
v_posterior = np.linalg.inv(np.linalg.inv(v_prior) + my_data.T.dot(my_data))
posterior_mean = nu_posterior * v_posterior
v_post_diag = np.expand_dims(np.diag(v_posterior), axis=1)
posterior_sd = np.sqrt(nu_posterior *
                       (v_posterior ** 2.0 + v_post_diag.dot(v_post_diag.T)))

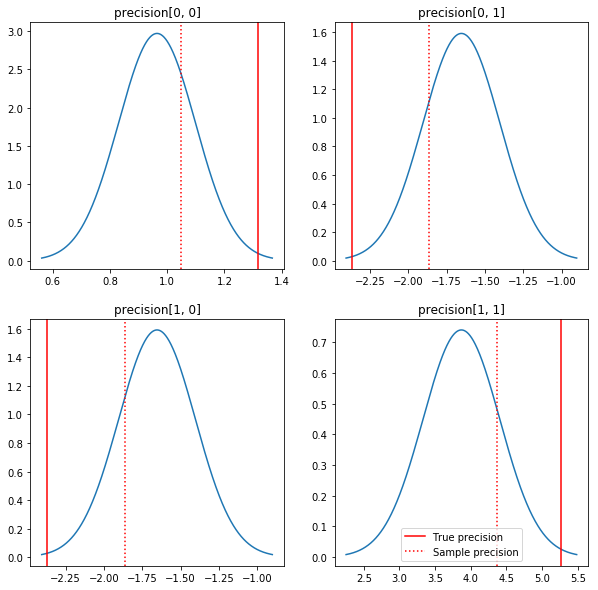
Un gráfico rápido de los posteriores y los valores reales. Tenga en cuenta que los posteriores están cerca de los posteriores de la muestra, pero se han encogido un poco hacia la identidad. Tenga en cuenta también que los valores verdaderos están bastante lejos de la moda del posterior; presumiblemente, esto se debe a que el anterior no es una coincidencia muy buena para nuestros datos. En un verdadero problema que nos gustaría probablemente hacemos mejor con algo parecido a una escala inversa Wishart antes de la covarianza (véase, por ejemplo, de Andrew Gelman comentario sobre el tema), pero entonces no tendría un buen posterior analítica.

sample_precision = np.linalg.inv(np.cov(my_data, rowvar=False, bias=False))
fig, axes = plt.subplots(2, 2)
fig.set_size_inches(10, 10)
for i in range(2):
  for j in range(2):
    ax = axes[i, j]
    loc = posterior_mean[i, j]
    scale = posterior_sd[i, j]
    xmin = loc - 3.0 * scale
    xmax = loc + 3.0 * scale
    x = np.linspace(xmin, xmax, 1000)
    y = scipy.stats.norm.pdf(x, loc=loc, scale=scale)
    ax.plot(x, y)
    ax.axvline(true_precision[i, j], color='red', label='True precision')
    ax.axvline(sample_precision[i, j], color='red', linestyle=':', label='Sample precision')
    ax.set_title('precision[%d, %d]' % (i, j))
plt.legend()
plt.show()

png

Paso 3: implementar la función de probabilidad en TensorFlow

Spoiler: Nuestro primer intento no va a funcionar; hablaremos de por qué a continuación.

Consejo: el uso TensorFlow modo ansiosos la hora de desarrollar sus funciones de verosimilitud. Modo ansiosos hace que se comportan más como TF NumPy - todo lo que se ejecuta inmediatamente, por lo que se puede depurar de forma interactiva en lugar de tener que utilizar Session.run() . Ver las notas aquí .

Preliminar: clases de distribución

TFP tiene una colección de clases de distribución que usaremos para generar nuestras probabilidades de registro. Una cosa a tener en cuenta es que estas clases funcionan con tensores de muestras en lugar de solo muestras individuales; esto permite la vectorización y aceleraciones relacionadas.

Una distribución puede funcionar con un tensor de muestras de 2 formas diferentes. Es más simple ilustrar estas 2 formas con un ejemplo concreto que involucra una distribución con un solo parámetro escalar. Voy a usar el Poisson distribución, que tiene una rate parámetro.

Si creamos una Poisson con un único valor para la rate parámetro, una llamada a la sample() método devuelve un solo valor. Este valor se denomina un event , y en este caso los eventos están todos los escalares.
Si creamos una Poisson con un tensor de valores para la rate parámetro, una llamada a la sample() método devuelve ahora varios valores, uno para cada valor de la tasa de tensor. El objeto actúa como una colección de Poissons independientes, cada uno con su propio ritmo, y cada uno de los valores devueltos por una llamada a la sample() corresponde a uno de estos Poissons. Esta colección de eventos independientes pero no idénticamente distribuidas se llama un batch .
La sample() método toma un sample_shape parámetro que por defecto es una tupla vacía. El paso de un valor no vacío para sample_shape resultados en la muestra que regresan múltiples lotes. Esta colección de lotes se denomina sample .

Una distribución de log_prob() método consume datos de manera que los paralelismos cómo sample() lo genera. log_prob() devuelve probabilidades para muestras, es decir, para múltiple, lotes independientes de eventos.

Si tenemos nuestro objeto de Poisson que se creó con un escalar rate , cada lote es un escalar, y si se pasa de un tensor de muestras, vamos a salir un tensor del mismo tamaño de las probabilidades de registro.
Si tenemos nuestro objeto de Poisson que se creó con un tensor de la forma de T de rate valores, cada lote es un tensor de la forma de T . Si pasamos un tensor de muestras de forma D, T, obtendremos un tensor de probabilidades logarítmicas de forma D, T.

A continuación se muestran algunos ejemplos que ilustran estos casos. Ver este portátil para un tutorial más detallado sobre los eventos, lotes y formas.

# case 1: get log probabilities for a vector of iid draws from a single
# normal distribution
norm1 = tfd.Normal(loc=0., scale=1.)
probs1 = norm1.log_prob(tf.constant([1., 0.5, 0.]))

# case 2: get log probabilities for a vector of independent draws from
# multiple normal distributions with different parameters.  Note the vector
# values for loc and scale in the Normal constructor.
norm2 = tfd.Normal(loc=[0., 2., 4.], scale=[1., 1., 1.])
probs2 = norm2.log_prob(tf.constant([1., 0.5, 0.]))

print('iid draws from a single normal:', probs1.numpy())
print('draws from a batch of normals:', probs2.numpy())

iid draws from a single normal: [-1.4189385 -1.0439385 -0.9189385]
draws from a batch of normals: [-1.4189385 -2.0439386 -8.918939 ]

Probabilidad del registro de datos

Primero implementaremos la función de probabilidad de registro de datos.

VALIDATE_ARGS = True
ALLOW_NAN_STATS = False

Una diferencia clave con el caso de NumPy es que nuestra función de verosimilitud TensorFlow necesitará manejar vectores de matrices de precisión en lugar de matrices simples. Los vectores de parámetros se usarán cuando muestreemos de múltiples cadenas.

Crearemos un objeto de distribución que funcione con un lote de matrices de precisión (es decir, una matriz por cadena).

Al calcular las probabilidades de registro de nuestros datos, necesitaremos que nuestros datos se repliquen de la misma manera que nuestros parámetros para que haya una copia por variable de lote. La forma de nuestros datos replicados deberá ser la siguiente:

[sample shape, batch shape, event shape]

En nuestro caso, la forma del evento es 2 (ya que estamos trabajando con gaussianos 2-D). La forma de la muestra es 100, ya que tenemos 100 muestras. La forma del lote será solo el número de matrices de precisión con las que estamos trabajando. Es un desperdicio replicar los datos cada vez que llamamos a la función de probabilidad, por lo que replicaremos los datos por adelantado y pasaremos la versión replicada.

Tenga en cuenta que se trata de una aplicación ineficaz: MultivariateNormalFullCovariance es caro en relación con algunas alternativas que hablaremos en la sección Optimización al final.

def log_lik_data(precisions, replicated_data):
  n = tf.shape(precisions)[0]  # number of precision matrices
  # We're estimating a precision matrix; we have to invert to get log
  # probabilities.  Cholesky inversion should be relatively efficient,
  # but as we'll see later, it's even better if we can avoid doing the Cholesky
  # decomposition altogether.
  precisions_cholesky = tf.linalg.cholesky(precisions)
  covariances = tf.linalg.cholesky_solve(
      precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
  rv_data = tfd.MultivariateNormalFullCovariance(
      loc=tf.zeros([n, 2]),
      covariance_matrix=covariances,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)

  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# For our test, we'll use a tensor of 2 precision matrices.
# We'll need to replicate our data for the likelihood function.
# Remember, TFP wants the data to be structured so that the sample dimensions
# are first (100 here), then the batch dimensions (2 here because we have 2
# precision matrices), then the event dimensions (2 because we have 2-D
# Gaussian data).  We'll need to add a middle dimension for the batch using
# expand_dims, and then we'll need to create 2 replicates in this new dimension
# using tile.
n = 2
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
print(replicated_data.shape)

(100, 2, 2)

Consejo: Una cosa que he encontrado para ser extremadamente útil es escribir pequeñas comprobaciones de validez de mis funciones TensorFlow. Es realmente fácil estropear la vectorización en TF, por lo que tener las funciones NumPy más simples es una excelente manera de verificar la salida de TF. Piense en ellos como pequeñas pruebas unitarias.

# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_data(precisions, replicated_data=replicated_data).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.8182

Probabilidad de registro previo

Lo anterior es más fácil ya que no tenemos que preocuparnos por la replicación de datos.

@tf.function(autograph=False)
def log_lik_prior(precisions):
  rv_precision = tfd.WishartTriL(
      df=PRIOR_DF,
      scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)
  return rv_precision.log_prob(precisions)

# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_prior(precisions).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]))
  print('tensorflow:', lik_tf[i])

0
numpy: -2.2351873809649625
tensorflow: -2.2351875
1
numpy: -9.103606346649766
tensorflow: -9.103608

Construya la función de verosimilitud logarítmica conjunta

La función de probabilidad del registro de datos anterior depende de nuestras observaciones, pero el muestreador no las tendrá. Podemos deshacernos de la dependencia sin usar una variable global usando un [cierre] (https://en.wikipedia.org/wiki/Closure_ (computer_programming). Los cierres involucran una función externa que construye un entorno que contiene las variables que necesita un función interna.

def get_log_lik(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik(precision):
    return log_lik_data(precision, replicated_data) + log_lik_prior(precision)

  return _log_lik

Paso 4: muestra

Ok, ¡es hora de probar! Para simplificar las cosas, solo usaremos 1 cadena y usaremos la matriz de identidad como punto de partida. Haremos las cosas con más cuidado más tarde.

Nuevamente, esto no va a funcionar, obtendremos una excepción.

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  init_precision = tf.expand_dims(tf.eye(2), axis=0)

  # Use expand_dims because we want to pass in a tensor of starting values
  log_lik_fn = get_log_lik(my_data, n_chains=1)

  # we'll just do a few steps here
  num_results = 10
  num_burnin_steps = 10
  states = tfp.mcmc.sample_chain(
     num_results=num_results,
     num_burnin_steps=num_burnin_steps,
     current_state=[
         init_precision,
     ],
     kernel=tfp.mcmc.HamiltonianMonteCarlo(
         target_log_prob_fn=log_lik_fn,
         step_size=0.1,
         num_leapfrog_steps=3),
     trace_fn=None,
     seed=123)
  return states

try:
  states = sample()
except Exception as e:
  # shorten the giant stack trace
  lines = str(e).split('\n')
  print('\n'.join(lines[:5]+['...']+lines[-3:]))

Cholesky decomposition was not successful. The input might not be valid.
     [[{ {node mcmc_sample_chain/trace_scan/while/body/_79/smart_for_loop/while/body/_371/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_537/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/StatefulPartitionedCall/Cholesky} }]] [Op:__inference_sample_2849]

Function call stack:
sample
...
Function call stack:
sample

Identificando el problema

InvalidArgumentError (see above for traceback): Cholesky decomposition was not successful. The input might not be valid. Eso no es muy útil. Veamos si podemos averiguar más sobre lo que sucedió.

Imprimiremos los parámetros para cada paso para que podamos ver el valor para el que fallan las cosas.
Agregaremos algunas afirmaciones para evitar problemas específicos.

Las afirmaciones son complicadas porque son operaciones de TensorFlow, y tenemos que cuidar que se ejecuten y no se optimicen fuera del gráfico. Vale la pena leer esta descripción general de TensorFlow depuración si usted no está familiarizado con las afirmaciones TF. Puede forzar explícitamente afirmaciones para ejecutar usando tf.control_dependencies (ver los comentarios en el código de abajo).

Nativa de TensorFlow Print función tiene el mismo comportamiento que las afirmaciones - es una operación, y hay que tener cierto cuidado para asegurarse de que se ejecuta. Print causa dolores de cabeza adicionales cuando estamos trabajando en un cuaderno: su producción se envía a stderr , y stderr no se muestra en la celda. Vamos a utilizar un truco aquí: en lugar de utilizar tf.Print , vamos a crear nuestra propia operación de impresión a través de TensorFlow tf.pyfunc . Al igual que con las afirmaciones, debemos asegurarnos de que nuestro método se ejecute.

def get_log_lik_verbose(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  def _log_lik(precisions):
    # An internal method we'll make into a TensorFlow operation via tf.py_func
    def _print_precisions(precisions):
      print('precisions:\n', precisions)
      return False  # operations must return something!
    # Turn our method into a TensorFlow operation
    print_op = tf.compat.v1.py_func(_print_precisions, [precisions], tf.bool)

    # Assertions are also operations, and some care needs to be taken to ensure
    # that they're executed
    assert_op = tf.assert_equal(
        precisions, tf.linalg.matrix_transpose(precisions),
        message='not symmetrical', summarize=4, name='symmetry_check')

    # The control_dependencies statement forces its arguments to be executed
    # before subsequent operations
    with tf.control_dependencies([print_op, assert_op]):
      return (log_lik_data(precisions, replicated_data) +
              log_lik_prior(precisions))

  return _log_lik

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  init_precision = tf.eye(2)[tf.newaxis, ...]
  log_lik_fn = get_log_lik_verbose(my_data)
  # we'll just do a few steps here
  num_results = 10
  num_burnin_steps = 10
  states = tfp.mcmc.sample_chain(
      num_results=num_results,
      num_burnin_steps=num_burnin_steps,
      current_state=[
          init_precision,
      ],
      kernel=tfp.mcmc.HamiltonianMonteCarlo(
          target_log_prob_fn=log_lik_fn,
          step_size=0.1,
          num_leapfrog_steps=3),
      trace_fn=None,
      seed=123)

try:
  states = sample()
except Exception as e:
  # shorten the giant stack trace
  lines = str(e).split('\n')
  print('\n'.join(lines[:5]+['...']+lines[-3:]))

precisions:
 [[[1. 0.]
  [0. 1.]]]
precisions:
 [[[1. 0.]
  [0. 1.]]]
precisions:
 [[[ 0.24315196 -0.2761638 ]
  [-0.33882257  0.8622    ]]]
 assertion failed: [not symmetrical] [Condition x == y did not hold element-wise:] [x (leapfrog_integrate_one_step/add:0) = ] [[[0.243151963 -0.276163787][-0.338822573 0.8622]]] [y (leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/matrix_transpose/transpose:0) = ] [[[0.243151963 -0.338822573][-0.276163787 0.8622]]]
     [[{ {node mcmc_sample_chain/trace_scan/while/body/_96/smart_for_loop/while/body/_381/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_503/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/symmetry_check_1/Assert/AssertGuard/else/_577/Assert} }]] [Op:__inference_sample_4837]

Function call stack:
sample
...
Function call stack:
sample

Por que esto falla

El primer valor de parámetro nuevo que prueba el muestreador es una matriz asimétrica. Eso hace que la descomposición de Cholesky falle, ya que solo se define para matrices simétricas (y definidas positivas).

El problema aquí es que nuestro parámetro de interés es una matriz de precisión, y las matrices de precisión deben ser reales, simétricas y definidas positivas. El muestreador no sabe nada sobre esta restricción (excepto posiblemente a través de gradientes), por lo que es muy posible que el muestreador proponga un valor no válido, dando lugar a una excepción, especialmente si el tamaño del paso es grande.

Con el muestreador Hamiltoniano Monte Carlo, es posible que podamos solucionar el problema utilizando un tamaño de paso muy pequeño, ya que el gradiente debe mantener los parámetros alejados de las regiones no válidas, pero los tamaños de paso pequeños significan una convergencia lenta. Con una muestra de Metropolis-Hastings, que no sabe nada sobre gradientes, estamos condenados.

Versión 2: reparametrización a parámetros sin restricciones

Hay una solución sencilla al problema anterior: podemos volver a parametrizar nuestro modelo de modo que los nuevos parámetros ya no tengan estas restricciones. TFP proporciona un conjunto útil de herramientas, bijectors, para hacer precisamente eso.

Reparametrización con biyectores

Nuestra matriz de precisión debe ser real y simétrica; queremos una parametrización alternativa que no tenga estas restricciones. Un punto de partida es una factorización Cholesky de la matriz de precisión. Los factores de Cholesky todavía están restringidos: son triangulares inferiores y sus elementos diagonales deben ser positivos. Sin embargo, si tomamos el logaritmo de las diagonales del factor de Cholesky, los logaritmos ya no están restringidos a ser positivos, y luego, si aplanamos la porción triangular inferior en un vector 1-D, ya no tenemos la restricción triangular inferior. . El resultado en nuestro caso será un vector de longitud 3 sin restricciones.

(El manual de Stan tiene un gran capítulo sobre el uso de transformaciones para eliminar diversos tipos de restricciones sobre los parámetros.)

Esta reparametrización tiene poco efecto en nuestra función de probabilidad de registro de datos, solo tenemos que invertir nuestra transformación para obtener la matriz de precisión, pero el efecto sobre la anterior es más complicado. Hemos especificado que la probabilidad de una matriz de precisión dada viene dada por la distribución de Wishart; ¿Cuál es la probabilidad de nuestra matriz transformada?

Recordemos que si aplicamos una función monótona \(g\) a un 1-D variable aleatoria \(X\), \(Y = g(X)\), la densidad para \(Y\) está dada por

\[ f_Y(y) = | \frac{d}{dy}(g^{-1}(y)) | f_X(g^{-1}(y)) \]

El derivado de \(g^{-1}\) término representa la forma en que \(g\) cambia volúmenes locales. Para las variables aleatorias de dimensiones superiores, el factor de corrección es el valor absoluto del determinante de la jacobiana de \(g^{-1}\) (ver aquí ).

Tendremos que agregar un jacobiano de la transformación inversa en nuestra función de probabilidad logarítmica previa. Felizmente, de la PTF Bijector clase puede hacerse cargo de esto para nosotros.

El Bijector clase se utiliza para representar funciones invertibles, lisas utilizados para el cambio de variables en funciones de densidad de probabilidad. Bijectors todos tienen un forward() método que realiza una transformación, una inverse() método que se invierte, y forward_log_det_jacobian() y inverse_log_det_jacobian() métodos que proporcionan las correcciones Jacobianas que necesitamos cuando reparaterize un pdf.

TFP proporciona una colección de bijectors útiles que podemos combinar través de la composición a través de la Chain operador para formar transformadas bastante complicado. En nuestro caso, compondremos los siguientes 3 biyectores (las operaciones en la cadena se realizan de derecha a izquierda):

El primer paso de nuestra transformación es realizar una factorización de Cholesky en la matriz de precisión. No hay una clase Bijector para eso; sin embargo, el CholeskyOuterProduct bijector toma el producto de 2 factores de Cholesky. Podemos utilizar la inversa de la operación utilizando el Invert operador.
El siguiente paso es tomar el logaritmo de los elementos diagonales del factor Cholesky. Esto lo logramos a través de la TransformDiagonal bijector y la inversa de la Exp bijector.
Finalmente aplanar la parte triangular inferior de la matriz a un vector usando la inversa de la FillTriangular bijector.

# Our transform has 3 stages that we chain together via composition:
precision_to_unconstrained = tfb.Chain([
    # step 3: flatten the lower triangular portion of the matrix
    tfb.Invert(tfb.FillTriangular(validate_args=VALIDATE_ARGS)),
    # step 2: take the log of the diagonals    
    tfb.TransformDiagonal(tfb.Invert(tfb.Exp(validate_args=VALIDATE_ARGS))),
    # step 1: decompose the precision matrix into its Cholesky factors
    tfb.Invert(tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS)),
])

# sanity checks
m = tf.constant([[1., 2.], [2., 8.]])
m_fwd = precision_to_unconstrained.forward(m)
m_inv = precision_to_unconstrained.inverse(m_fwd)

# bijectors handle tensors of values, too!
m2 = tf.stack([m, tf.eye(2)])
m2_fwd = precision_to_unconstrained.forward(m2)
m2_inv = precision_to_unconstrained.inverse(m2_fwd)

print('single input:')
print('m:\n', m.numpy())
print('precision_to_unconstrained(m):\n', m_fwd.numpy())
print('inverse(precision_to_unconstrained(m)):\n', m_inv.numpy())
print()

print('tensor of inputs:')
print('m2:\n', m2.numpy())
print('precision_to_unconstrained(m2):\n', m2_fwd.numpy())
print('inverse(precision_to_unconstrained(m2)):\n', m2_inv.numpy())

single input:
m:
 [[1. 2.]
 [2. 8.]]
precision_to_unconstrained(m):
 [0.6931472 2.        0.       ]
inverse(precision_to_unconstrained(m)):
 [[1. 2.]
 [2. 8.]]

tensor of inputs:
m2:
 [[[1. 2.]
  [2. 8.]]

 [[1. 0.]
  [0. 1.]]]
precision_to_unconstrained(m2):
 [[0.6931472 2.        0.       ]
 [0.        0.        0.       ]]
inverse(precision_to_unconstrained(m2)):
 [[[1. 2.]
  [2. 8.]]

 [[1. 0.]
  [0. 1.]]]

El TransformedDistribution clase automatiza el proceso de aplicación de un bijector a una distribución y haciendo que la corrección jacobiana necesario log_prob() . Nuestro nuevo prior se convierte en:

def log_lik_prior_transformed(transformed_precisions):
  rv_precision = tfd.TransformedDistribution(
      tfd.WishartTriL(
          df=PRIOR_DF,
          scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
          validate_args=VALIDATE_ARGS,
          allow_nan_stats=ALLOW_NAN_STATS),
      bijector=precision_to_unconstrained,
      validate_args=VALIDATE_ARGS)
  return rv_precision.log_prob(transformed_precisions)

# Check against the numpy implementation.  Note that when comparing, we need
# to add in the Jacobian correction.
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_prior_transformed(transformed_precisions).numpy()
corrections = precision_to_unconstrained.inverse_log_det_jacobian(
    transformed_precisions, event_ndims=1).numpy()
n = precisions.shape[0]

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
  print('tensorflow:', lik_tf[i])

0
numpy: -0.8488930160357633
tensorflow: -0.84889317
1
numpy: -7.305657151741624
tensorflow: -7.305659

Solo necesitamos invertir la transformación para nuestra probabilidad de registro de datos:

precision = precision_to_unconstrained.inverse(transformed_precision)

Dado que en realidad queremos la factorización Cholesky de la matriz de precisión, sería más eficiente hacer solo una inversa parcial aquí. Sin embargo, dejaremos la optimización para más adelante y dejaremos el inverso parcial como un ejercicio para el lector.

def log_lik_data_transformed(transformed_precisions, replicated_data):
  # We recover the precision matrix by inverting our bijector.  This is
  # inefficient since we really want the Cholesky decomposition of the
  # precision matrix, and the bijector has that in hand during the inversion,
  # but we'll worry about efficiency later.
  n = tf.shape(transformed_precisions)[0]
  precisions = precision_to_unconstrained.inverse(transformed_precisions)
  precisions_cholesky = tf.linalg.cholesky(precisions)
  covariances = tf.linalg.cholesky_solve(
      precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
  rv_data = tfd.MultivariateNormalFullCovariance(
      loc=tf.zeros([n, 2]),
      covariance_matrix=covariances,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)

  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# sanity check
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_data_transformed(
    transformed_precisions, replicated_data).numpy()

for i in range(precisions.shape[0]):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.8182

Nuevamente envolvemos nuestras nuevas funciones en un cierre.

def get_log_lik_transformed(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik_transformed(transformed_precisions):
    return (log_lik_data_transformed(transformed_precisions, replicated_data) +
            log_lik_prior_transformed(transformed_precisions))

  return _log_lik_transformed

# make sure everything runs
log_lik_fn = get_log_lik_transformed(my_data)
m = tf.eye(2)[tf.newaxis, ...]
lik = log_lik_fn(precision_to_unconstrained.forward(m)).numpy()
print(lik)

[-431.5611]

Muestreo

Ahora que no tenemos que preocuparnos de que nuestro muestreador explote debido a valores de parámetros no válidos, generemos algunas muestras reales.

El muestreador funciona con la versión sin restricciones de nuestros parámetros, por lo que debemos transformar nuestro valor inicial en su versión sin restricciones. Las muestras que generamos también estarán en su forma no restringida, por lo que debemos transformarlas nuevamente. Los biyectores están vectorizados, por lo que es fácil hacerlo.

# We'll choose a proper random initial value this time
np.random.seed(123)
initial_value_cholesky = np.array(
    [[0.5 + np.random.uniform(), 0.0],
     [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
    dtype=np.float32)
initial_value =  initial_value_cholesky.dot(
  initial_value_cholesky.T)[np.newaxis, ...]

# The sampler works with unconstrained values, so we'll transform our initial
# value
initial_value_transformed = precision_to_unconstrained.forward(
  initial_value).numpy()

# Sample!
@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_transformed(my_data, n_chains=1)

  num_results = 1000
  num_burnin_steps = 1000

  states, is_accepted = tfp.mcmc.sample_chain(
      num_results=num_results,
      num_burnin_steps=num_burnin_steps,
      current_state=[
          initial_value_transformed,
      ],
      kernel=tfp.mcmc.HamiltonianMonteCarlo(
          target_log_prob_fn=log_lik_fn,
          step_size=0.1,
          num_leapfrog_steps=3),
      trace_fn=lambda _, pkr: pkr.is_accepted,
      seed=123)
  # transform samples back to their constrained form
  precision_samples = [precision_to_unconstrained.inverse(s) for s in states]
  return states, precision_samples, is_accepted

states, precision_samples, is_accepted = sample()

¡Comparemos la media de la salida de nuestro muestreador con la media posterior analítica!

print('True posterior mean:\n', posterior_mean)
print('Sample mean:\n', np.mean(np.reshape(precision_samples, [-1, 2, 2]), axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Sample mean:
 [[ 1.4315274  -0.25587553]
 [-0.25587553  0.5740424 ]]

¡Estamos muy lejos! Averigüemos por qué. Primero echemos un vistazo a nuestras muestras.

np.reshape(precision_samples, [-1, 2, 2])

array([[[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       ...,

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]]], dtype=float32)

Uh oh, parece que todos tienen el mismo valor. Averigüemos por qué.

El kernel_results_ variable es una tupla con nombre que se da información sobre la toma de muestras en cada estado. El is_accepted campo es la clave aquí.

# Look at the acceptance for the last 100 samples
print(np.squeeze(is_accepted)[-100:])
print('Fraction of samples accepted:', np.mean(np.squeeze(is_accepted)))

[False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False]
Fraction of samples accepted: 0.0

¡Todas nuestras muestras fueron rechazadas! Presumiblemente, nuestro tamaño de paso era demasiado grande. Elegí stepsize=0.1 puramente arbitraria.

Versión 3: muestreo con un tamaño de paso adaptativo

Dado que el muestreo con mi elección arbitraria de tamaño de paso falló, tenemos algunos elementos de la agenda:

implementar un tamaño de paso adaptativo, y
realizar algunas comprobaciones de convergencia.

Hay algunos ejemplos de código agradable en tensorflow_probability/python/mcmc/hmc.py para la implementación de tamaños de paso de adaptación. Lo he adaptado a continuación.

Tenga en cuenta que hay una separada sess.run() declaración para cada paso. Esto es realmente útil para la depuración, ya que nos permite agregar fácilmente algunos diagnósticos por paso si es necesario. Por ejemplo, podemos mostrar un progreso incremental, cronometrar cada paso, etc.

Consejo: Una forma aparentemente común a estropear su muestreo es que su cultivo gráfico en el bucle. (La razón para finalizar el gráfico antes de que se ejecute la sesión es para evitar este tipo de problemas). Sin embargo, si no ha estado usando finalize (), una verificación de depuración útil si su código se ralentiza es imprimir el gráfico tamaño en cada paso a través de len(mygraph.get_operations()) - si se incrementa la longitud, es probable que hacer algo malo.

Vamos a ejecutar 3 cadenas independientes aquí. Hacer algunas comparaciones entre las cadenas nos ayudará a verificar la convergencia.

# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3

np.random.seed(123)

initial_values = []
for i in range(N_CHAINS):
  initial_value_cholesky = np.array(
      [[0.5 + np.random.uniform(), 0.0],
       [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
      dtype=np.float32)
  initial_values.append(initial_value_cholesky.dot(initial_value_cholesky.T))
initial_values = np.stack(initial_values)

initial_values_transformed = precision_to_unconstrained.forward(
  initial_values).numpy()

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_transformed(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=hmc,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states, is_accepted = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values_transformed,
      kernel=adapted_kernel,
      trace_fn=lambda _, pkr: pkr.inner_results.is_accepted,
      parallel_iterations=1)
  # transform samples back to their constrained form
  precision_samples = precision_to_unconstrained.inverse(states)
  return states, precision_samples, is_accepted

states, precision_samples, is_accepted = sample()

Una comprobación rápida: nuestra tasa de aceptación durante nuestro muestreo está cerca de nuestro objetivo de 0,651.

print(np.mean(is_accepted))

0.6190666666666667

Aún mejor, la media de nuestra muestra y la desviación estándar están cerca de lo que esperamos de la solución analítica.

precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.96426415 -1.6519215 ]
 [-1.6519215   3.8614824 ]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13622096 0.25235635]
 [0.25235635 0.5394968 ]]

Comprobando la convergencia

En general, no tendremos una solución analítica con la que comparar, por lo que tendremos que asegurarnos de que el muestreador haya convergido. Una verificación estándar es el Gelman-Rubin \(\hat{R}\) estadística, que requiere múltiples cadenas de muestreo. \(\hat{R}\) mide el grado en que la varianza (de los medios) entre las cadenas supera lo que uno esperaría si las cadenas se distribuyeron de forma idéntica. Los valores de \(\hat{R}\) cerca de 1 se usan para indicar la convergencia aproximada. Ver la fuente para más detalles.

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0038308 1.0005717]
 [1.0005717 1.0006068]]

Crítica de modelos

Si no tuviéramos una solución analítica, este sería el momento de hacer una crítica real del modelo.

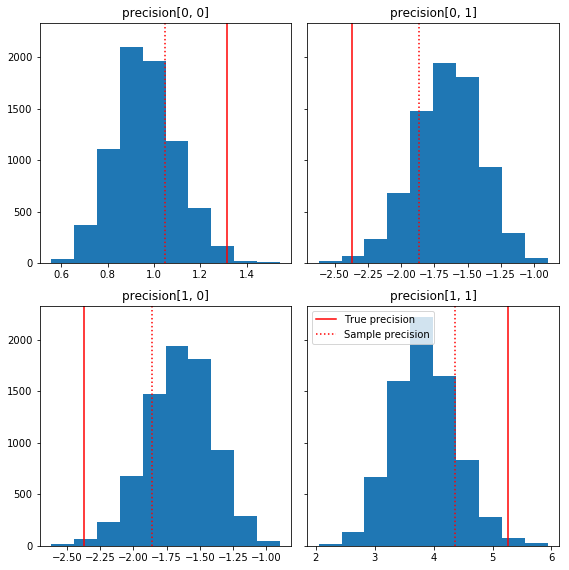
Aquí hay algunos histogramas rápidos de los componentes de la muestra en relación con nuestra verdad básica (en rojo). Tenga en cuenta que las muestras se han reducido de los valores de la matriz de precisión de la muestra hacia la matriz de identidad anterior.

fig, axes = plt.subplots(2, 2, sharey=True)
fig.set_size_inches(8, 8)
for i in range(2):
  for j in range(2):
    ax = axes[i, j]
    ax.hist(precision_samples_reshaped[:, i, j])
    ax.axvline(true_precision[i, j], color='red',
               label='True precision')
    ax.axvline(sample_precision[i, j], color='red', linestyle=':',
               label='Sample precision')
    ax.set_title('precision[%d, %d]' % (i, j))
plt.tight_layout()
plt.legend()
plt.show()

png

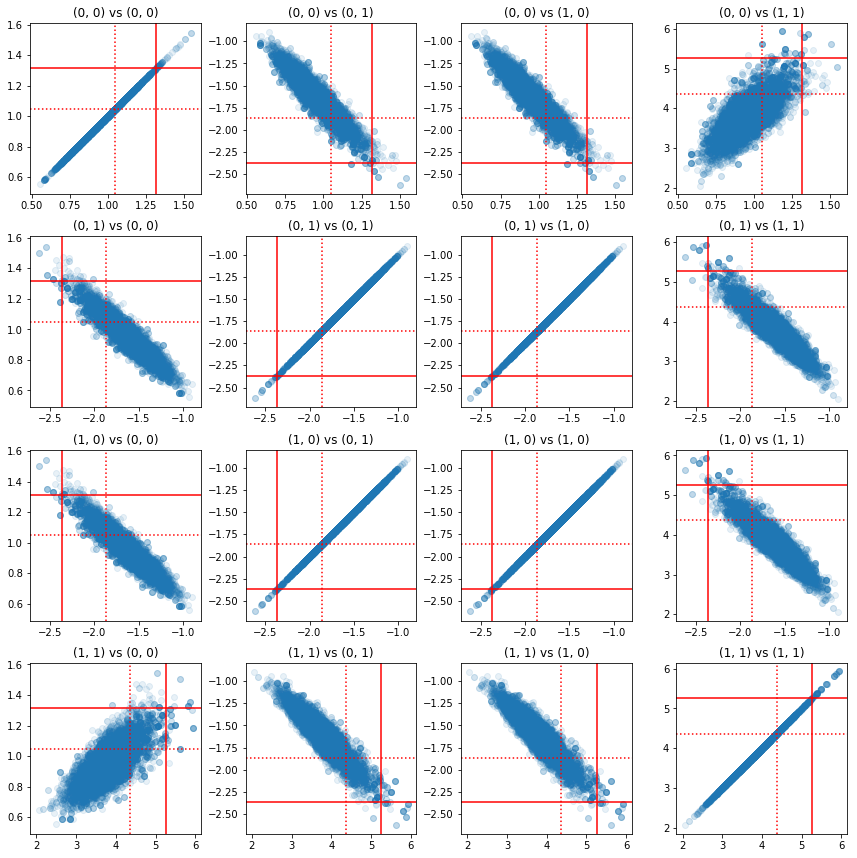
Algunas gráficas de dispersión de pares de componentes de precisión muestran que debido a la estructura de correlación de la parte posterior, los verdaderos valores posteriores no son tan improbables como aparecen en los marginales anteriores.

fig, axes = plt.subplots(4, 4)
fig.set_size_inches(12, 12)
for i1 in range(2):
  for j1 in range(2):
    index1 = 2 * i1 + j1
    for i2 in range(2):
      for j2 in range(2):
        index2 = 2 * i2 + j2
        ax = axes[index1, index2]
        ax.scatter(precision_samples_reshaped[:, i1, j1],
                   precision_samples_reshaped[:, i2, j2], alpha=0.1)
        ax.axvline(true_precision[i1, j1], color='red')
        ax.axhline(true_precision[i2, j2], color='red')
        ax.axvline(sample_precision[i1, j1], color='red', linestyle=':')
        ax.axhline(sample_precision[i2, j2], color='red', linestyle=':')
        ax.set_title('(%d, %d) vs (%d, %d)' % (i1, j1, i2, j2))
plt.tight_layout()
plt.show()

png

Versión 4: muestreo más simple de parámetros restringidos

Bijectors hizo que el muestreo de la matriz de precisión fuera sencillo, pero hubo una gran cantidad de conversión manual hacia y desde la representación sin restricciones. ¡Hay una manera más fácil!

La Transición TransformadaKernel

El TransformedTransitionKernel simplifica este proceso. Envuelve su muestra y maneja todas las conversiones. Toma como argumento una lista de biyectores que asignan valores de parámetros no restringidos a valores restringidos. Así que aquí tenemos la inversa de la precision_to_unconstrained bijector hemos utilizado anteriormente. Podríamos simplemente usamos tfb.Invert(precision_to_unconstrained) , pero que implicaría tomar de los inversos de los inversos (TensorFlow no es lo suficientemente inteligente como para simplificar tf.Invert(tf.Invert()) a tf.Identity()) , así que en vez Escribiré un nuevo biyector.

Restringir biyector

# The bijector we need for the TransformedTransitionKernel is the inverse of
# the one we used above
unconstrained_to_precision = tfb.Chain([
    # step 3: take the product of Cholesky factors
    tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS),
    # step 2: exponentiate the diagonals    
    tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
    # step 1: map a vector to a lower triangular matrix
    tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])

# quick sanity check
m = [[1., 2.], [2., 8.]]
m_inv = unconstrained_to_precision.inverse(m).numpy()
m_fwd = unconstrained_to_precision.forward(m_inv).numpy()

print('m:\n', m)
print('unconstrained_to_precision.inverse(m):\n', m_inv)
print('forward(unconstrained_to_precision.inverse(m)):\n', m_fwd)

m:
 [[1.0, 2.0], [2.0, 8.0]]
unconstrained_to_precision.inverse(m):
 [0.6931472 2.        0.       ]
forward(unconstrained_to_precision.inverse(m)):
 [[1. 2.]
 [2. 8.]]

Muestreo con TransformedTransitionKernel

Con la TransformedTransitionKernel , ya no tenemos que hacer transformaciones manuales de nuestros parámetros. Nuestros valores iniciales y nuestras muestras son todas matrices de precisión; solo tenemos que pasar nuestro (s) biyector (es) ilimitado (s) al kernel y se encarga de todas las transformaciones.

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  ttk = tfp.mcmc.TransformedTransitionKernel(
      inner_kernel=hmc, bijector=unconstrained_to_precision)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=ttk,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values,
      kernel=adapted_kernel,
      trace_fn=None,
      parallel_iterations=1)
  # transform samples back to their constrained form
  return states

precision_samples  = sample()

Comprobando la convergencia

El \(\hat{R}\) de verificación de convergencia ve bien!

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0013582 1.0019467]
 [1.0019467 1.0011805]]

Comparación con la analítica posterior

De nuevo, comparemos con el posterior analítico.

# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])

print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.96687526 -1.6552585 ]
 [-1.6552585   3.867676  ]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13329624 0.24913791]
 [0.24913791 0.53983927]]

Optimizaciones

Ahora que tenemos todo funcionando de un extremo a otro, hagamos una versión más optimizada. La velocidad no importa demasiado para este ejemplo, pero una vez que las matrices se hacen más grandes, algunas optimizaciones marcarán una gran diferencia.

Una gran mejora de velocidad que podemos hacer es reparametrizar en términos de la descomposición de Cholesky. La razón es que nuestra función de verosimilitud de datos requiere tanto la covarianza como las matrices de precisión. Inversión de la matriz es caro (\(O(n^3)\) para una \(n \times n\) matriz), y si parametrizamos en términos de la covarianza o la matriz de precisión, tenemos que hacer una inversión para obtener la otra.

Como recordatorio, un verdadero,, simétrico matriz definida positiva \(M\) se puede descomponer en un producto de la forma \(M = L L^T\) donde la matriz \(L\) es triangular inferior y tiene diagonales positivos. Dada la descomposición de Cholesky de \(M\), podemos obtener de manera más eficiente tanto \(M\) (el producto de una inferior y una matriz triangular superior) y \(M^{-1}\) (a través de back-sustitución). La factorización de Cholesky en sí no es barata de calcular, pero si parametrizamos en términos de factores de Cholesky, solo necesitamos calcular la factorización de Choleksy de los valores de los parámetros iniciales.

Usando la descomposición de Cholesky de la matriz de covarianza

TFP tiene una versión de la distribución normal multivariable, MultivariateNormalTriL , que se parametriza en términos del factor de Cholesky de la matriz de covarianza. Entonces, si tuviéramos que parametrizar en términos del factor de Cholesky de la matriz de covarianza, podríamos calcular la probabilidad del registro de datos de manera eficiente. El desafío consiste en calcular la probabilidad logarítmica anterior con una eficiencia similar.

Si tuviéramos una versión de la distribución de Wishart inversa que funcionara con factores Cholesky de muestras, estaríamos listos. Por desgracia, no lo hacemos. (¡Sin embargo, el equipo agradecería el envío de códigos!) Como alternativa, podemos usar una versión de la distribución Wishart que funcione con factores Cholesky de muestras junto con una cadena de biyectores.

Por el momento, nos faltan algunos biyectores de serie para hacer las cosas realmente eficientes, pero quiero mostrar el proceso como un ejercicio y una ilustración útil del poder de los biyectores de TFP.

Una distribución de Wishart que opera con factores Cholesky

El Wishart distribución tiene una bandera útil, input_output_cholesky , que especifica que las matrices de entrada y salida deben ser factores de Cholesky. Es más eficiente y numéricamente ventajoso trabajar con los factores de Cholesky que con matrices completas, razón por la cual esto es deseable. Un punto importante sobre la semántica de la bandera: es sólo una indicación de que la representación de la entrada y salida a la distribución debe cambiar - no indica una reparametrización total de la distribución, lo que implicaría una corrección Jacobiano a la log_prob() función. De hecho, queremos hacer esta reparametrización completa, así que crearemos nuestra propia distribución.

# An optimized Wishart distribution that has been transformed to operate on
# Cholesky factors instead of full matrices.  Note that we gain a modest
# additional speedup by specifying the Cholesky factor of the scale matrix
# (i.e. by passing in the scale_tril parameter instead of scale).

class CholeskyWishart(tfd.TransformedDistribution):
  """Wishart distribution reparameterized to use Cholesky factors."""
  def __init__(self,
      df,
      scale_tril,
      validate_args=False,
      allow_nan_stats=True,
      name='CholeskyWishart'):
    # Wishart has a bunch of methods that we want to support but not
    # implement.  We'll subclass TransformedDistribution here to take care of
    # those.  We'll override the few for which speed is critical and implement
    # them with a separate Wishart for which input_output_cholesky=True
    super(CholeskyWishart, self).__init__(
        distribution=tfd.WishartTriL(
            df=df,
            scale_tril=scale_tril,
            input_output_cholesky=False,
            validate_args=validate_args,
            allow_nan_stats=allow_nan_stats),
        bijector=tfb.Invert(tfb.CholeskyOuterProduct()),
        validate_args=validate_args,
        name=name
    )
    # Here's the Cholesky distribution we'll use for log_prob() and sample()
    self.cholesky = tfd.WishartTriL(
        df=df,
        scale_tril=scale_tril,
        input_output_cholesky=True,
        validate_args=validate_args,
        allow_nan_stats=allow_nan_stats)

  def _log_prob(self, x):
    return (self.cholesky.log_prob(x) +
            self.bijector.inverse_log_det_jacobian(x, event_ndims=2))

  def _sample_n(self, n, seed=None):
    return self.cholesky._sample_n(n, seed)

# some checks
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)

@tf.function(autograph=False)
def compute_log_prob(m):
  w_transformed = tfd.TransformedDistribution(
      tfd.WishartTriL(df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY),
      bijector=tfb.Invert(tfb.CholeskyOuterProduct()))
  w_optimized = CholeskyWishart(
      df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY)
  log_prob_transformed = w_transformed.log_prob(m)
  log_prob_optimized = w_optimized.log_prob(m)
  return log_prob_transformed, log_prob_optimized

for matrix in [np.eye(2, dtype=np.float32),
               np.array([[1., 0.], [2., 8.]], dtype=np.float32)]:
  log_prob_transformed, log_prob_optimized = [
      t.numpy() for t in compute_log_prob(matrix)]
  print('Transformed Wishart:', log_prob_transformed)
  print('Optimized Wishart', log_prob_optimized)

Transformed Wishart: -0.84889317
Optimized Wishart -0.84889317
Transformed Wishart: -99.269455
Optimized Wishart -99.269455

Construyendo una distribución Wishart inversa

Tenemos nuestra matriz de covarianza \(C\) descompone en \(C = L L^T\) donde \(L\) es triangular inferior y tiene una diagonal positivo. Queremos saber la probabilidad de \(L\) dado que \(C \sim W^{-1}(\nu, V)\) donde \(W^{-1}\) es la distribución de Wishart.

La distribución de Wishart inversa tiene la propiedad de que si \(C \sim W^{-1}(\nu, V)\), entonces la matriz de precisión \(C^{-1} \sim W(\nu, V^{-1})\). Así podemos obtener la probabilidad de \(L\) a través de un TransformedDistribution que toma como parámetros de la distribución de Wishart y una bijector que mapea el factor de Cholesky de la matriz de precisión a un factor de Cholesky de su inversa.

Una manera directa (pero no muy eficiente) para llegar desde el factor de Cholesky de \(C^{-1}\) a \(L\) es invertir el factor de Cholesky por la espalda de problemas, entonces la formación de la matriz de covarianza de estos factores invertidas, y luego hacer una factorización de Cholesky .

Dejar que la descomposición de Cholesky de \(C^{-1} = M M^T\). \(M\) es triangular inferior, por lo que podemos invertir usando el MatrixInverseTriL bijector.

Formando \(C\) de \(M^{-1}\) es un poco complicado: \(C = (M M^T)^{-1} = M^{-T}M^{-1} = M^{-T} (M^{-T})^T\). \(M\) es triangular inferior, de modo \(M^{-1}\) también será menor triangular, y \(M^{-T}\) será triangular superior. El CholeskyOuterProduct() bijector solo funciona con matrices triangulares inferiores, por lo que no podemos usarlo para formar \(C\) de \(M^{-T}\). Nuestra solución es una cadena de biyectores que permutan las filas y columnas de una matriz.

Por suerte, esta lógica se encapsula en el CholeskyToInvCholesky bijector!

Combinando todas las piezas

# verify that the bijector works
m = np.array([[1., 0.], [2., 8.]], dtype=np.float32)
c_inv = m.dot(m.T)
c = np.linalg.inv(c_inv)
c_chol = np.linalg.cholesky(c)
wishart_cholesky_to_iw_cholesky = tfb.CholeskyToInvCholesky()
w_fwd = wishart_cholesky_to_iw_cholesky.forward(m).numpy()

print('numpy =\n', c_chol)
print('bijector =\n', w_fwd)

numpy =
 [[ 1.0307764   0.        ]
 [-0.03031695  0.12126781]]
bijector =
 [[ 1.0307764   0.        ]
 [-0.03031695  0.12126781]]

Nuestra distribución final

Nuestro Wishart inverso que opera en factores Cholesky es el siguiente:

inverse_wishart_cholesky = tfd.TransformedDistribution(
    distribution=CholeskyWishart(
        df=PRIOR_DF,
        scale_tril=np.linalg.cholesky(np.linalg.inv(PRIOR_SCALE))),
    bijector=tfb.CholeskyToInvCholesky())

Tenemos nuestro Wishart inverso, pero es algo lento porque tenemos que hacer una descomposición de Cholesky en el biyector. Regresemos a la parametrización de la matriz de precisión y veamos qué podemos hacer allí para la optimización.

Versión final (!): Usando la descomposición de Cholesky de la matriz de precisión

Un enfoque alternativo es trabajar con factores de Cholesky de la matriz de precisión. Aquí, la función de probabilidad previa es fácil de calcular, pero la función de probabilidad del registro de datos requiere más trabajo ya que la TFP no tiene una versión de la normal multivariada que esté parametrizada por precisión.

Probabilidad de logaritmo previo optimizada

Usamos el CholeskyWishart distribución construimos anteriormente para construir el anterior.

# Our new prior.
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)

def log_lik_prior_cholesky(precisions_cholesky):
  rv_precision = CholeskyWishart(
      df=PRIOR_DF,
      scale_tril=PRIOR_SCALE_CHOLESKY,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)
  return rv_precision.log_prob(precisions_cholesky)

# Check against the slower TF implementation and the NumPy implementation.
# Note that when comparing to NumPy, we need to add in the Jacobian correction.
precisions = [np.eye(2, dtype=np.float32),
              true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
lik_tf = log_lik_prior_cholesky(precisions_cholesky).numpy()
lik_tf_slow = tfd.TransformedDistribution(
    distribution=tfd.WishartTriL(
        df=PRIOR_DF, scale_tril=tf.linalg.cholesky(PRIOR_SCALE)),
    bijector=tfb.Invert(tfb.CholeskyOuterProduct())).log_prob(
    precisions_cholesky).numpy()
corrections = tfb.Invert(tfb.CholeskyOuterProduct()).inverse_log_det_jacobian(
    precisions_cholesky, event_ndims=2).numpy()
n = precisions.shape[0]

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
  print('tensorflow slow:', lik_tf_slow[i])
  print('tensorflow fast:', lik_tf[i])

0
numpy: -0.8488930160357633
tensorflow slow: -0.84889317
tensorflow fast: -0.84889317
1
numpy: -7.442875031036973
tensorflow slow: -7.442877
tensorflow fast: -7.442876

Probabilidad de registro de datos optimizada

We can use TFP's bijectors to build our own version of the multivariate normal. Here is the key idea:

Suppose I have a column vector \(X\) whose elements are iid samples of \(N(0, 1)\). We have \(\text{mean}(X) = 0\) and \(\text{cov}(X) = I\)

Now let \(Y = A X + b\). We have \(\text{mean}(Y) = b\) and \(\text{cov}(Y) = A A^T\)

Hence we can make vectors with mean \(b\) and covariance \(C\) using the affine transform \(Ax+b\) to vectors of iid standard Normal samples provided \(A A^T = C\). The Cholesky decomposition of \(C\) has the desired property. However, there are other solutions.

Let \(P = C^{-1}\) and let the Cholesky decomposition of \(P\) be \(B\), ie \(B B^T = P\). Now

\(P^{-1} = (B B^T)^{-1} = B^{-T} B^{-1} = B^{-T} (B^{-T})^T\)

So another way to get our desired mean and covariance is to use the affine transform \(Y=B^{-T}X + b\).

Our approach (courtesy of this notebook ):

Use tfd.Independent() to combine a batch of 1-D Normal random variables into a single multi-dimensional random variable. The reinterpreted_batch_ndims parameter for Independent() specifies the number of batch dimensions that should be reinterpreted as event dimensions. In our case we create a 1-D batch of length 2 that we transform into a 1-D event of length 2, so reinterpreted_batch_ndims=1 .
Apply a bijector to add the desired covariance: tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky, adjoint=True)) . Note that above we're multiplying our iid normal random variables by the transpose of the inverse of the Cholesky factor of the precision matrix \((B^{-T}X)\). The tfb.Invert takes care of inverting \(B\), and the adjoint=True flag performs the transpose.
Apply a bijector to add the desired offset: tfb.Shift(shift=shift) Note that we have to do the shift as a separate step from the initial inverted affine transform because otherwise the inverted scale is applied to the shift (since the inverse of \(y=Ax+b\) is \(x=A^{-1}y - A^{-1}b\)).

class MVNPrecisionCholesky(tfd.TransformedDistribution):
  """Multivariate normal parameterized by loc and Cholesky precision matrix."""

  def __init__(self, loc, precision_cholesky, name=None):
    super(MVNPrecisionCholesky, self).__init__(
        distribution=tfd.Independent(
            tfd.Normal(loc=tf.zeros_like(loc),
                       scale=tf.ones_like(loc)),
            reinterpreted_batch_ndims=1),
        bijector=tfb.Chain([
            tfb.Shift(shift=loc),
            tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky,
                                  adjoint=True)),
        ]),
        name=name)

@tf.function(autograph=False)
def log_lik_data_cholesky(precisions_cholesky, replicated_data):
  n = tf.shape(precisions_cholesky)[0]  # number of precision matrices
  rv_data = MVNPrecisionCholesky(
      loc=tf.zeros([n, 2]),
      precision_cholesky=precisions_cholesky)
  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# check against the numpy implementation
true_precision_cholesky = np.linalg.cholesky(true_precision)
precisions = [np.eye(2, dtype=np.float32), true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
n = precisions_cholesky.shape[0]
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
lik_tf = log_lik_data_cholesky(precisions_cholesky, replicated_data).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.81824

Combined log likelihood function

Now we combine our prior and data log likelihood functions in a closure.

def get_log_lik_cholesky(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik_cholesky(precisions_cholesky):
    return (log_lik_data_cholesky(precisions_cholesky, replicated_data) +
            log_lik_prior_cholesky(precisions_cholesky))

  return _log_lik_cholesky

Constraining bijector

Our samples are constrained to be valid Cholesky factors, which means they must be lower triangular matrices with positive diagonals. The TransformedTransitionKernel needs a bijector that maps unconstrained tensors to/from tensors with our desired constraints. We've removed the Cholesky decomposition from the bijector's inverse, which speeds things up.

unconstrained_to_precision_cholesky = tfb.Chain([
    # step 2: exponentiate the diagonals    
    tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
    # step 1: expand the vector to a lower triangular matrix
    tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])

# some checks
inv = unconstrained_to_precision_cholesky.inverse(precisions_cholesky).numpy()
fwd = unconstrained_to_precision_cholesky.forward(inv).numpy()
print('precisions_cholesky:\n', precisions_cholesky)
print('\ninv:\n', inv)
print('\nfwd(inv):\n', fwd)

precisions_cholesky:
 [[[ 1.         0.       ]
  [ 0.         1.       ]]

 [[ 1.1470785  0.       ]
  [-2.0647411  1.0000004]]]

inv:
 [[ 0.0000000e+00  0.0000000e+00  0.0000000e+00]
 [ 3.5762781e-07 -2.0647411e+00  1.3721828e-01]]

fwd(inv):
 [[[ 1.         0.       ]
  [ 0.         1.       ]]

 [[ 1.1470785  0.       ]
  [-2.0647411  1.0000004]]]

Initial values

We generate a tensor of initial values. We're working with Cholesky factors, so we generate some Cholesky factor initial values.

# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3

np.random.seed(123)

initial_values_cholesky = []
for i in range(N_CHAINS):
  initial_values_cholesky.append(np.array(
      [[0.5 + np.random.uniform(), 0.0],
       [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
      dtype=np.float32))
initial_values_cholesky = np.stack(initial_values_cholesky)

Sampling

We sample N_CHAINS chains using the TransformedTransitionKernel .

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_cholesky(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  ttk = tfp.mcmc.TransformedTransitionKernel(
      inner_kernel=hmc, bijector=unconstrained_to_precision_cholesky)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=ttk,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values,
      kernel=adapted_kernel,
      trace_fn=None,
      parallel_iterations=1)
  # transform samples back to their constrained form
  samples = tf.linalg.matmul(states, states, transpose_b=True)
  return samples

precision_samples = sample()

Convergence check

A quick convergence check looks good:

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0013583 1.0019467]
 [1.0019467 1.0011804]]

Comparing results to the analytic posterior

# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, newshape=[-1, 2, 2])

And again, the sample means and standard deviations match those of the analytic posterior.

print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.9668749 -1.6552604]
 [-1.6552604  3.8676758]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13329637 0.24913797]
 [0.24913797 0.53983945]]

Ok, all done! We've got our optimized sampler working.