 TensorFlow.org এ দেখুন TensorFlow.org এ দেখুন |  Google Colab-এ চালান Google Colab-এ চালান |  GitHub-এ উৎস দেখুন GitHub-এ উৎস দেখুন |  নোটবুক ডাউনলোড করুন নোটবুক ডাউনলোড করুন |
TensorFlow সম্ভাব্যতা শেখার জন্য আমি এই নোটবুকটি কেস স্টাডি হিসেবে লিখেছি। আমি যে সমস্যাটি সমাধান করতে বেছে নিয়েছি তা হল একটি 2-D মানে 0 গাউসিয়ান র্যান্ডম ভেরিয়েবলের নমুনার জন্য একটি কোভেরিয়েন্স ম্যাট্রিক্স অনুমান করা। সমস্যাটির কয়েকটি চমৎকার বৈশিষ্ট্য রয়েছে:
- আমরা যদি কোভেরিয়েন্সের আগে একটি বিপরীত উইশার্ট ব্যবহার করি (একটি সাধারণ পদ্ধতি), সমস্যাটির একটি বিশ্লেষণাত্মক সমাধান রয়েছে, তাই আমরা আমাদের ফলাফলগুলি পরীক্ষা করতে পারি।
- সমস্যাটিতে একটি সীমাবদ্ধ প্যারামিটারের নমুনা নেওয়া জড়িত, যা কিছু আকর্ষণীয় জটিলতা যোগ করে।
- সবচেয়ে সহজ সমাধানটি দ্রুততম নয়, তাই কিছু অপ্টিমাইজেশন কাজ করতে হবে।
আমি আমার অভিজ্ঞতা লেখার সিদ্ধান্ত নিয়েছি। TFP এর সূক্ষ্ম পয়েন্টগুলির চারপাশে আমার মাথা মোড়ানোর জন্য আমার কিছু সময় লেগেছে, তাই এই নোটবুকটি মোটামুটি সহজভাবে শুরু হয় এবং তারপর ধীরে ধীরে আরও জটিল TFP বৈশিষ্ট্যগুলিতে কাজ করে৷ আমি পথ ধরে অনেক সমস্যার মধ্যে পড়েছিলাম, এবং আমি উভয় প্রক্রিয়াগুলিকে ক্যাপচার করার চেষ্টা করেছি যা আমাকে তাদের সনাক্ত করতে সাহায্য করেছিল এবং আমি অবশেষে যে সমাধানগুলি পেয়েছি। আমি (পরীক্ষার নিশ্চিত পৃথক পদক্ষেপ সঠিক করতে প্রচুর সহ) বিস্তারিত প্রচুর অন্তর্ভুক্ত করার চেষ্টা করেছি।
কেন টেনসরফ্লো সম্ভাব্যতা শিখবেন?
আমি কিছু কারণের জন্য আমার প্রকল্পের জন্য TensorFlow সম্ভাবনাকে আবেদনময়ী পেয়েছি:
- TensorFlow সম্ভাব্যতা আপনাকে একটি নোটবুকে ইন্টারেক্টিভভাবে জটিল মডেলের প্রোটোটাইপ করতে দেয়। আপনি আপনার কোডটিকে ছোট ছোট টুকরো টুকরো করে দিতে পারেন যা আপনি ইন্টারেক্টিভভাবে এবং ইউনিট পরীক্ষার মাধ্যমে পরীক্ষা করতে পারেন।
- একবার আপনি স্কেল বাড়াতে প্রস্তুত হয়ে গেলে, আপনি একাধিক মেশিনে একাধিক, অপ্টিমাইজড প্রসেসরে টেনসরফ্লো চালানোর জন্য আমাদের কাছে থাকা সমস্ত অবকাঠামোর সুবিধা নিতে পারেন।
- অবশেষে, যখন আমি সত্যিই স্ট্যান পছন্দ করি, তখন ডিবাগ করা আমার কাছে বেশ কঠিন। আপনাকে আপনার সমস্ত মডেলিং কোড একটি স্বতন্ত্র ভাষায় লিখতে হবে যাতে আপনাকে আপনার কোডে খোঁচা দিতে, মধ্যবর্তী রাজ্যগুলি পরিদর্শন করতে এবং আরও অনেক কিছু করার জন্য খুব কম সরঞ্জাম রয়েছে।
নেতিবাচক দিক হল TensorFlow সম্ভাব্যতা Stan এবং PyMC3 এর থেকে অনেক নতুন, তাই ডকুমেন্টেশনের কাজ চলছে, এবং অনেক কার্যকারিতা তৈরি করা বাকি আছে। সুখের বিষয়, আমি TFP-এর ভিত্তিকে শক্ত বলে খুঁজে পেয়েছি, এবং এটি একটি মডুলার উপায়ে ডিজাইন করা হয়েছে যা একজনকে এর কার্যকারিতা মোটামুটি সহজভাবে প্রসারিত করতে দেয়। এই নোটবুকে, কেস স্টাডি সমাধান করার পাশাপাশি, আমি TFP প্রসারিত করার কিছু উপায় দেখাব।
এটা কার জন্য
আমি অনুমান করছি যে পাঠকরা কিছু গুরুত্বপূর্ণ পূর্বশর্ত নিয়ে এই নোটবুকে আসছেন। তোমার উচিত:
- বায়েসিয়ান ইনফারেন্সের বুনিয়াদি জানুন। (আপনি না থাকে, একটি সত্যিই চমৎকার প্রথম বই পরিসংখ্যানগত ভান্ডারের চিন্তা )
- একটি এমসিএমসি স্যাম্পলিং গ্রন্থাগার, যেমন সঙ্গে কিছু পরিচিত আছে স্ট্যান / PyMC3 / বাগ
- একটি কঠিন কাছে আছে NumPy (এক ভাল ইন্ট্রো হয় ডেটা বিশ্লেষণ জন্য পাইথন )
- সঙ্গে অন্তত পাসিং পরিচিত আছে TensorFlow , কিন্তু না অগত্যা দক্ষতার। ( শিক্ষণ TensorFlow ভাল জিনিস, কিন্তু TensorFlow দ্রুত বিবর্তন মানে সবচেয়ে বই একটু তারিখের হবে। স্ট্যানফোর্ড এর CS20 অবশ্যই ভাল হয়।)
প্রথম প্রচেষ্টা
এখানে সমস্যা এ আমার প্রথম প্রচেষ্টা. স্পয়লার: আমার সমাধান কাজ করে না, এবং জিনিসগুলি ঠিক করার জন্য এটি বেশ কয়েকটি প্রচেষ্টা নিতে যাচ্ছে! যদিও প্রক্রিয়াটি কিছুটা সময় নেয়, নীচের প্রতিটি প্রচেষ্টা TFP এর একটি নতুন অংশ শেখার জন্য কার্যকর হয়েছে।
একটি নোট: TFP বর্তমানে ইনভার্স উইশার্ট ডিস্ট্রিবিউশন বাস্তবায়ন করে না (আমরা শেষে দেখব কীভাবে আমাদের নিজস্ব ইনভার্স উইশার্ট রোল করতে হয়), তাই এর পরিবর্তে আমি উইশার্টের পূর্বে ব্যবহার করে একটি নির্ভুল ম্যাট্রিক্স অনুমান করার সমস্যাটিকে পরিবর্তন করব।
import collections
import math
import os
import time
import numpy as np
import pandas as pd
import scipy
import scipy.stats
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
ধাপ 1: একসাথে পর্যবেক্ষণ পান
এখানে আমার ডেটা সমস্ত সিন্থেটিক, তাই এটি একটি বাস্তব-বিশ্বের উদাহরণের চেয়ে কিছুটা পরিপাটি বলে মনে হচ্ছে। যাইহোক, এমন কোন কারণ নেই যে আপনি নিজের কিছু সিন্থেটিক ডেটা তৈরি করতে পারবেন না।
টিপ: একবার আপনি আপনার মডেল ফর্মে সিদ্ধান্ত নিয়েছে করেছি, আপনি কিছু পরামিতির মান বাছাই এবং আপনার নির্বাচিত মডেল ব্যবহার কিছু কৃত্রিম তথ্য জেনারেট করতে পারবেন না। আপনার বাস্তবায়নের একটি বিচক্ষণতা পরীক্ষা হিসাবে, আপনি তারপর যাচাই করতে পারেন যে আপনার অনুমানগুলি আপনার বেছে নেওয়া পরামিতিগুলির সত্যিকারের মানগুলি অন্তর্ভুক্ত করে৷ আপনার ডিবাগিং/পরীক্ষা চক্রকে দ্রুততর করতে, আপনি আপনার মডেলের একটি সরলীকৃত সংস্করণ বিবেচনা করতে পারেন (যেমন কম মাত্রা বা কম নমুনা ব্যবহার করুন)।
টিপ: এটা NumPy অ্যারে হিসাবে আপনার পর্যবেক্ষণের সঙ্গে কাজ করার সবচেয়ে সহজ হচ্ছে। উল্লেখ্য একটি গুরুত্বপূর্ণ বিষয় হল NumPy ডিফল্টভাবে float64 ব্যবহার করে, যখন TensorFlow ডিফল্টভাবে float32 ব্যবহার করে।
সাধারণভাবে, TensorFlow ক্রিয়াকলাপগুলি সমস্ত আর্গুমেন্টকে একই ধরণের হতে চায় এবং প্রকারগুলি পরিবর্তন করতে আপনাকে সুস্পষ্ট ডেটা কাস্টিং করতে হবে। আপনি যদি float64 পর্যবেক্ষণ ব্যবহার করেন, তাহলে আপনাকে প্রচুর কাস্ট অপারেশন যোগ করতে হবে। NumPy, বিপরীতে, স্বয়ংক্রিয়ভাবে কাস্টিংয়ের যত্ন নেবে। অত: পর, এটা অনেক সহজ float32 আপনার Numpy তথ্য রূপান্তর করতে তুলনায় এটি ব্যবহার float64 করার TensorFlow বলপূর্বক হয়।
কিছু প্যারামিটার মান নির্বাচন করুন
# We're assuming 2-D data with a known true mean of (0, 0)
true_mean = np.zeros([2], dtype=np.float32)
# We'll make the 2 coordinates correlated
true_cor = np.array([[1.0, 0.9], [0.9, 1.0]], dtype=np.float32)
# And we'll give the 2 coordinates different variances
true_var = np.array([4.0, 1.0], dtype=np.float32)
# Combine the variances and correlations into a covariance matrix
true_cov = np.expand_dims(np.sqrt(true_var), axis=1).dot(
np.expand_dims(np.sqrt(true_var), axis=1).T) * true_cor
# We'll be working with precision matrices, so we'll go ahead and compute the
# true precision matrix here
true_precision = np.linalg.inv(true_cov)
# Here's our resulting covariance matrix
print(true_cov)
# Verify that it's positive definite, since np.random.multivariate_normal
# complains about it not being positive definite for some reason.
# (Note that I'll be including a lot of sanity checking code in this notebook -
# it's a *huge* help for debugging)
print('eigenvalues: ', np.linalg.eigvals(true_cov))
[[4. 1.8] [1.8 1. ]] eigenvalues: [4.843075 0.15692513]
কিছু সিন্থেটিক পর্যবেক্ষণ তৈরি করুন
নোট TensorFlow সম্ভাব্যতা কনভেনশন যে আপনার ডেটার প্রাথমিক মাত্রা (গুলি) নমুনা সূচকের প্রতিনিধিত্ব ব্যবহার করে, এবং আপনার ডেটা চূড়ান্ত মাত্রা (গুলি) আপনার নমুনার মাত্রা প্রতিনিধিত্ব করে।
এখানে আমরা চাই 100 নমুনা দৈর্ঘ্যের একটি ভেক্টর, যেগুলির প্রতিটি 2. আমরা একটি অ্যারের তৈরি করে দেব my_data আকৃতি (100, 2) সঙ্গে। my_data[i, :] হয় \(i\)তম নমুনা, এবং এটি 2 দৈর্ঘ্যের একটি ভেক্টর হয়।
(করতে করতে মনে রাখুন my_data টাইপ float32 আছে!)
# Set the seed so the results are reproducible.
np.random.seed(123)
# Now generate some observations of our random variable.
# (Note that I'm suppressing a bunch of spurious about the covariance matrix
# not being positive semidefinite via check_valid='ignore' because it really is
# positive definite!)
my_data = np.random.multivariate_normal(
mean=true_mean, cov=true_cov, size=100,
check_valid='ignore').astype(np.float32)
my_data.shape
(100, 2)
বিচক্ষণতা পর্যবেক্ষণ পরীক্ষা
বাগগুলির একটি সম্ভাব্য উৎস হল আপনার সিন্থেটিক ডেটা নষ্ট করা! এর কিছু সহজ চেক করা যাক.
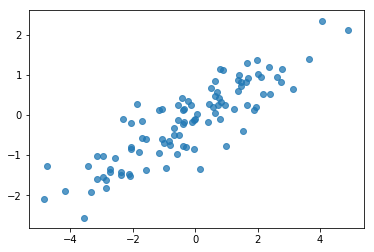
# Do a scatter plot of the observations to make sure they look like what we
# expect (higher variance on the x-axis, y values strongly correlated with x)
plt.scatter(my_data[:, 0], my_data[:, 1], alpha=0.75)
plt.show()
print('mean of observations:', np.mean(my_data, axis=0))
print('true mean:', true_mean)
mean of observations: [-0.24009615 -0.16638893] true mean: [0. 0.]
print('covariance of observations:\n', np.cov(my_data, rowvar=False))
print('true covariance:\n', true_cov)
covariance of observations: [[3.95307734 1.68718486] [1.68718486 0.94910269]] true covariance: [[4. 1.8] [1.8 1. ]]
ঠিক আছে, আমাদের নমুনাগুলি যুক্তিসঙ্গত দেখাচ্ছে। পরবর্তী পর্ব.
ধাপ 2: NumPy-এ সম্ভাবনা ফাংশন প্রয়োগ করুন
TF সম্ভাব্যতাতে আমাদের MCMC স্যাম্পলিং সম্পাদন করার জন্য আমাদের যে প্রধান জিনিসটি লিখতে হবে তা হল একটি লগ সম্ভাবনা ফাংশন। সাধারণভাবে NumPy-এর তুলনায় TF লিখতে কিছুটা জটিল, তাই NumPy-এ প্রাথমিক বাস্তবায়ন করা আমার কাছে সহায়ক বলে মনে হয়। আমি 2 টুকরা, একটি ডাটা সম্ভাবনা ফাংশন যে অনুরূপ মধ্যে সম্ভাবনা ফাংশন বিভক্ত করতে যাচ্ছি \(P(data | parameters)\) এবং পূর্বে সম্ভাবনা ফাংশন অনুরূপ যে \(P(parameters)\)।
মনে রাখবেন যে এই NumPy ফাংশনগুলিকে সুপার অপ্টিমাইজ/ভেক্টরাইজ করতে হবে না কারণ লক্ষ্য হল পরীক্ষার জন্য কিছু মান তৈরি করা। শুদ্ধতা মূল বিবেচনা!
প্রথমে আমরা ডেটা লগ সম্ভাবনা অংশ বাস্তবায়ন করব। যে বেশ সোজা. একটি জিনিস মনে রাখবেন যে আমরা নির্ভুল ম্যাট্রিক্সের সাথে কাজ করতে যাচ্ছি, তাই আমরা সেই অনুযায়ী প্যারামিটারাইজ করব।
def log_lik_data_numpy(precision, data):
# np.linalg.inv is a really inefficient way to get the covariance matrix, but
# remember we don't care about speed here
cov = np.linalg.inv(precision)
rv = scipy.stats.multivariate_normal(true_mean, cov)
return np.sum(rv.logpdf(data))
# test case: compute the log likelihood of the data given the true parameters
log_lik_data_numpy(true_precision, my_data)
-280.81822950593767
আমরা সেখানে যেহেতু অবর জন্য একটি বিশ্লেষণাত্মক সমাধান বিশ্বকাপ পূর্বে স্পষ্টতা ম্যাট্রিক্স জন্য ব্যবহার করতে (দেখুন চলুন অনুবন্ধী গতকাল দেশের সর্বোচ্চ তাপমাত্রা এর উইকিপিডিয়ার কুশলী টেবিল )।
বিশ্বকাপ বন্টন 2 প্যারামিটার আছে:
- স্বাধীন ডিগ্রীগুলির সংখ্যা (লেবেল \(\nu\) উইকিপিডিয়া)
- স্কেলে ম্যাট্রিক্স (লেবেল \(V\) উইকিপিডিয়া)
পরামিতি সঙ্গে একটি বিশ্বকাপ বিতরণের জন্য গড় \(\nu, V\) হয় \(E[W] = \nu V\)এবং ভ্যারিয়েন্স হয় \(\text{Var}(W_{ij}) = \nu(v_{ij}^2+v_{ii}v_{jj})\)
কিছু দরকারী স্বজ্ঞা: আপনি উৎপাদিত দ্বারা একটি বিশ্বকাপ নমুনা তৈরি করতে পারেন \(\nu\) স্বাধীন স্বপক্ষে \(x_1 \ldots x_{\nu}\) গড় 0 এবং সহভেদাংক সঙ্গে একটি বহুচলকীয় স্বাভাবিক দৈব চলক থেকে \(V\) এবং তারপর সমষ্টি বিরচন \(W = \sum_{i=1}^{\nu} x_i x_i^T\)।
আপনি তাদের দ্বারা ভাগ বিশ্বকাপ নমুনা rescale তাহলে \(\nu\), আপনি নমুনা সহভেদাংক ম্যাট্রিক্স পেতে \(x_i\)। এই নমুনা সহভেদাংক ম্যাট্রিক্স দিকে ঝোঁক উচিত \(V\) যেমন \(\nu\) বাড়ে। যখন \(\nu\) ছোট, সেখানে নমুনা সহভেদাংক ম্যাট্রিক্স তারতম্য প্রচুর, এর এত ছোট মান হয় \(\nu\) দুর্বল গতকাল দেশের সর্বোচ্চ তাপমাত্রা এবং বৃহৎ মান মিলা \(\nu\) শক্তিশালী গতকাল দেশের সর্বোচ্চ তাপমাত্রা মিলা। লক্ষ্য করুন \(\nu\) অন্তত স্থান তুমি স্যাম্পলিং অথবা আপনি একবচন ম্যাট্রিক্স তৈরি করে দেব মাত্রা মত বৃহৎ হতে হবে।
আমরা ব্যবহার করব \(\nu = 3\) তাই আমরা একটি দুর্বল পূর্বে আছে, এবং আমরা নেব \(V = \frac{1}{\nu} I\) যা (রিকল এর মানে পরিচয় দিকে আমাদের সহভেদাংক অনুমান টান হবে \(\nu V\))।
PRIOR_DF = 3
PRIOR_SCALE = np.eye(2, dtype=np.float32) / PRIOR_DF
def log_lik_prior_numpy(precision):
rv = scipy.stats.wishart(df=PRIOR_DF, scale=PRIOR_SCALE)
return rv.logpdf(precision)
# test case: compute the prior for the true parameters
log_lik_prior_numpy(true_precision)
-9.103606346649766
বিশ্বকাপ বন্টন পরিচিত গড় সঙ্গে একটি বহুচলকীয় স্বাভাবিক স্পষ্টতা ম্যাট্রিক্স আনুমানিক হিসাব জন্য অনুবন্ধী পূর্বে হয় \(\mu\)।
ধরুন পূর্বে বিশ্বকাপ পরামিতি হয় \(\nu, V\) এবং যে আমরা আছে \(n\) আমাদের বহুচলকীয় স্বাভাবিক, পর্যবেক্ষণ \(x_1, \ldots, x_n\)। অবর পরামিতি হয় \(n + \nu, \left(V^{-1} + \sum_{i=1}^n (x_i-\mu)(x_i-\mu)^T \right)^{-1}\)।
n = my_data.shape[0]
nu_prior = PRIOR_DF
v_prior = PRIOR_SCALE
nu_posterior = nu_prior + n
v_posterior = np.linalg.inv(np.linalg.inv(v_prior) + my_data.T.dot(my_data))
posterior_mean = nu_posterior * v_posterior
v_post_diag = np.expand_dims(np.diag(v_posterior), axis=1)
posterior_sd = np.sqrt(nu_posterior *
(v_posterior ** 2.0 + v_post_diag.dot(v_post_diag.T)))
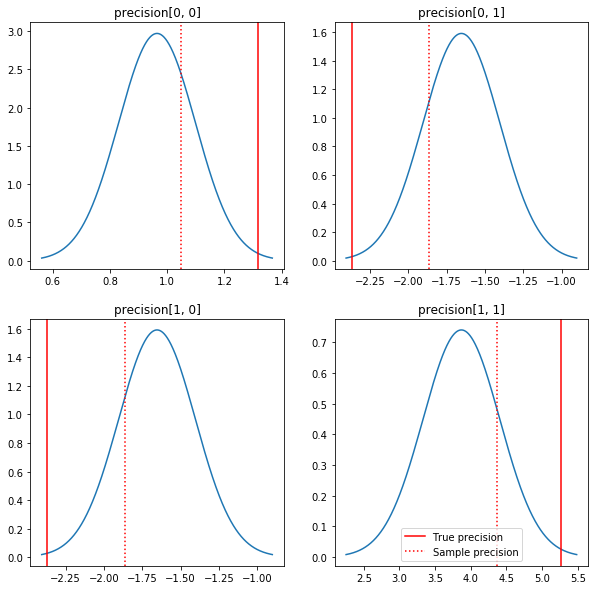
পোস্টেরিয়র এবং সত্যিকারের মানগুলির একটি দ্রুত প্লট। নোট করুন যে পোস্টেরিয়রগুলি নমুনা পোস্টেরিয়ারের কাছাকাছি কিন্তু পরিচয়ের দিকে কিছুটা সঙ্কুচিত হয়৷ এছাড়াও মনে রাখবেন যে সত্যিকারের মানগুলি পোস্টেরিয়র মোড থেকে বেশ দূরে - সম্ভবত এটি এই কারণে যে পূর্ব আমাদের ডেটার জন্য খুব ভাল মিল নয়৷ একটি বাস্তব সমস্যা আমরা সম্ভবত একটি সহভেদাংক জন্য পূর্বের বিশ্বকাপ বিপরীত ছোটো ভালো কিছু সাথে উন্নত করতে চাই (দেখুন, উদাহরণস্বরূপ, অ্যান্ড্রু Gelman এর ভাষ্য বিষয়ে), কিন্তু তারপর আমরা একটা চমৎকার বিশ্লেষণ অবর হতো না।
sample_precision = np.linalg.inv(np.cov(my_data, rowvar=False, bias=False))
fig, axes = plt.subplots(2, 2)
fig.set_size_inches(10, 10)
for i in range(2):
for j in range(2):
ax = axes[i, j]
loc = posterior_mean[i, j]
scale = posterior_sd[i, j]
xmin = loc - 3.0 * scale
xmax = loc + 3.0 * scale
x = np.linspace(xmin, xmax, 1000)
y = scipy.stats.norm.pdf(x, loc=loc, scale=scale)
ax.plot(x, y)
ax.axvline(true_precision[i, j], color='red', label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':', label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.legend()
plt.show()
ধাপ 3: TensorFlow-এ সম্ভাবনা ফাংশন প্রয়োগ করুন
স্পয়লার: আমাদের প্রথম প্রচেষ্টা কাজ করতে যাচ্ছে না; আমরা নীচে কেন সম্পর্কে কথা বলতে হবে.
টিপ: ব্যবহার TensorFlow উৎসুক মোড যখন আপনার সম্ভাবনা ফাংশন উন্নয়নশীল। অবিলম্বে, তাই আপনি ইন্টারেক্টিভ ব্যবহার করতে থাকার পরিবর্তে ডিবাগ করতে পারেন সবকিছু, executes - উৎসুক মোড মেমরি আচরণ আরো NumPy মত তোলে Session.run() । নোট দেখুন এখানে ।
প্রাথমিক: বিতরণ ক্লাস
TFP-এ বিতরণ ক্লাসের একটি সংগ্রহ রয়েছে যা আমরা আমাদের লগ সম্ভাব্যতা তৈরি করতে ব্যবহার করব। একটি বিষয় লক্ষণীয় যে এই ক্লাসগুলি শুধুমাত্র একক নমুনার পরিবর্তে নমুনার টেনসরের সাথে কাজ করে - এটি ভেক্টরাইজেশন এবং সম্পর্কিত গতির জন্য অনুমতি দেয়।
একটি বিতরণ 2টি ভিন্ন উপায়ে নমুনার টেনসরের সাথে কাজ করতে পারে। একটি একক স্কেলার প্যারামিটার সহ একটি বন্টন জড়িত একটি কংক্রিট উদাহরণ দিয়ে এই 2টি উপায়কে চিত্রিত করা সবচেয়ে সহজ। আমি ব্যবহার করব পইসন বন্টন, যা হয়েছে rate প্যারামিটার।
- আমরা যদি জন্য একটি একক মান সহ কোনো পইসন তৈরি
rateপরামিতি, তার একটি কলsample()পদ্ধতি একটি একক মান ফিরে। এই মান একটি বলা হয়event, এবং এই ক্ষেত্রে ঘটনা সব scalars হয়। - তাহলে আমরা জন্য মূল্যবোধের টেন্সর সঙ্গে একটি পইসন তৈরি
rateপরামিতি, তার একটি কলsample()পদ্ধতি এখন একাধিক মান ফেরৎ, হার টেন্সর প্রতিটি মান জন্য। বস্তু স্বাধীন Poissons একটি সংগ্রহ, তার নিজস্ব হার দিয়ে প্রতিটি হিসাবে কাজ করে, এবং মান প্রতিটি একটি কল দ্বারা ফিরেsample()এই Poissons এক অনুরূপ। স্বাধীন কিন্তু অভিন্নরুপে বিতরণ ঘটনা এই সংগ্রহে একটি বলা হয়batch। -
sample()পদ্ধতি লাগেsample_shapeএকটি খালি tuple করার পরামিতি, যা অক্ষমতা। জন্য একটি খালি মান পাসিংsample_shapeনমুনা ফলাফল একাধিক ব্যাচ ফিরিয়ে আনে। ব্যাচ এই সংগ্রহে একটি বলা হয়sample।
একটি ডিস্ট্রিবিউশনের log_prob() পদ্ধতি এমনভাবে ব্যবহার করা যাতে সমান্তরাল কিভাবে ডাটা হ্রাস sample() এটা তৈরি করে। log_prob() একাধিক জন্য নমুনার জন্য সম্ভাব্যতা, অর্থাত্, ঘটনা স্বাধীন ব্যাচ ফেরৎ।
- আমরা আমাদের পইসন বস্তুর স্কেলের সঙ্গে তৈরি করা হয়েছিল যে যদি
rate, প্রতিটি ব্যাচ স্কেলের, এবং যদি আমরা স্যাম্পেলের একটি টেন্সর মধ্যে পাস, আমরা লগ সম্ভাব্যতার একই আকারের একটি টেন্সর আউট পাবেন। - আমরা আমাদের পইসন বস্তুর আকৃতি একটি টেন্সর সঙ্গে তৈরি করা হয়েছিল যে যদি
Tএরrateমান, প্রতিটি ব্যাচ আকৃতি একটি টেন্সর হয়T। যদি আমরা D, T আকৃতির নমুনার একটি টেনসর পাস করি, তাহলে আমরা D, T আকৃতির লগ সম্ভাব্যতার একটি টেনসর বের করব।
নিচে কিছু উদাহরণ দেওয়া হল যা এই ঘটনাগুলিকে ব্যাখ্যা করে৷ দেখুন এই নোটবুক ঘটনা, ব্যাচ, এবং আকার উপর আরো বিস্তারিত টিউটোরিয়ালের জন্য।
# case 1: get log probabilities for a vector of iid draws from a single
# normal distribution
norm1 = tfd.Normal(loc=0., scale=1.)
probs1 = norm1.log_prob(tf.constant([1., 0.5, 0.]))
# case 2: get log probabilities for a vector of independent draws from
# multiple normal distributions with different parameters. Note the vector
# values for loc and scale in the Normal constructor.
norm2 = tfd.Normal(loc=[0., 2., 4.], scale=[1., 1., 1.])
probs2 = norm2.log_prob(tf.constant([1., 0.5, 0.]))
print('iid draws from a single normal:', probs1.numpy())
print('draws from a batch of normals:', probs2.numpy())
iid draws from a single normal: [-1.4189385 -1.0439385 -0.9189385] draws from a batch of normals: [-1.4189385 -2.0439386 -8.918939 ]
ডেটা লগ সম্ভাবনা
প্রথমে আমরা ডেটা লগ সম্ভাবনা ফাংশন বাস্তবায়ন করব।
VALIDATE_ARGS = True
ALLOW_NAN_STATS = False
NumPy কেস থেকে একটি মূল পার্থক্য হল যে আমাদের TensorFlow সম্ভাবনা ফাংশনকে শুধুমাত্র একক ম্যাট্রিক্সের পরিবর্তে নির্ভুল ম্যাট্রিসের ভেক্টরগুলি পরিচালনা করতে হবে। যখন আমরা একাধিক চেইন থেকে নমুনা করি তখন প্যারামিটারের ভেক্টর ব্যবহার করা হবে।
আমরা একটি ডিস্ট্রিবিউশন অবজেক্ট তৈরি করব যা নির্ভুল ম্যাট্রিক্সের ব্যাচের সাথে কাজ করে (অর্থাৎ প্রতি চেইনে একটি ম্যাট্রিক্স)।
আমাদের ডেটার লগ সম্ভাব্যতা গণনা করার সময়, আমাদের প্যারামিটারগুলির মতো একই পদ্ধতিতে আমাদের ডেটা প্রতিলিপি করা দরকার যাতে প্রতি ব্যাচ ভেরিয়েবলে একটি কপি থাকে। আমাদের প্রতিলিপিকৃত ডেটার আকৃতিটি নিম্নরূপ হতে হবে:
[sample shape, batch shape, event shape]
আমাদের ক্ষেত্রে, ইভেন্টের আকার 2 (যেহেতু আমরা 2-D গাউসিয়ানদের সাথে কাজ করছি)। নমুনা আকার 100, যেহেতু আমাদের 100টি নমুনা রয়েছে। ব্যাচের আকারটি হবে কেবলমাত্র নির্ভুল ম্যাট্রিক্সের সংখ্যা যার সাথে আমরা কাজ করছি। যতবার আমরা সম্ভাবনা ফাংশনকে কল করি ততবার ডেটা প্রতিলিপি করা অযথা, তাই আমরা আগে থেকেই ডেটার প্রতিলিপি তৈরি করব এবং প্রতিলিপিকৃত সংস্করণে পাস করব।
লক্ষ্য করুন এই একটি অদক্ষ বাস্তবায়ন হল: MultivariateNormalFullCovariance কিছু বিকল্প ব্যয়বহুল আপেক্ষিক যে আমরা শেষে অপ্টিমাইজেশান বিভাগে সম্পর্কে কথা বলতে পাবেন।
def log_lik_data(precisions, replicated_data):
n = tf.shape(precisions)[0] # number of precision matrices
# We're estimating a precision matrix; we have to invert to get log
# probabilities. Cholesky inversion should be relatively efficient,
# but as we'll see later, it's even better if we can avoid doing the Cholesky
# decomposition altogether.
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# For our test, we'll use a tensor of 2 precision matrices.
# We'll need to replicate our data for the likelihood function.
# Remember, TFP wants the data to be structured so that the sample dimensions
# are first (100 here), then the batch dimensions (2 here because we have 2
# precision matrices), then the event dimensions (2 because we have 2-D
# Gaussian data). We'll need to add a middle dimension for the batch using
# expand_dims, and then we'll need to create 2 replicates in this new dimension
# using tile.
n = 2
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
print(replicated_data.shape)
(100, 2, 2)
টিপ: আমি কেবল একটা বিষয় অত্যন্ত সহায়ক আমার TensorFlow ফাংশন সামান্য মানসিক সুস্থতা চেক লেখা হয় হতে পেয়েছি। TF-এ ভেক্টরাইজেশন এলোমেলো করা সত্যিই সহজ, তাই চারপাশে সহজ NumPy ফাংশন থাকা TF আউটপুট যাচাই করার একটি দুর্দান্ত উপায়। এগুলিকে ছোট ইউনিট পরীক্ষা হিসাবে ভাবুন।
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_data(precisions, replicated_data=replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
পূর্ব লগ সম্ভাবনা
আগেরটি সহজ কারণ আমাদের ডেটা প্রতিলিপি সম্পর্কে চিন্তা করতে হবে না।
@tf.function(autograph=False)
def log_lik_prior(precisions):
rv_precision = tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions)
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_prior(precisions).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]))
print('tensorflow:', lik_tf[i])
0 numpy: -2.2351873809649625 tensorflow: -2.2351875 1 numpy: -9.103606346649766 tensorflow: -9.103608
যৌথ লগ সম্ভাবনা ফাংশন তৈরি করুন
উপরের ডেটা লগ সম্ভাবনা ফাংশন আমাদের পর্যবেক্ষণের উপর নির্ভর করে, কিন্তু স্যাম্পলারের কাছে সেগুলি থাকবে না। আমরা একটি [ক্লোজার](https://en.wikipedia.org/wiki/Closure_(computer_programming) ব্যবহার করে একটি গ্লোবাল ভেরিয়েবল ব্যবহার না করে নির্ভরতা থেকে মুক্তি পেতে পারি। অভ্যন্তরীণ ফাংশন।
def get_log_lik(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik(precision):
return log_lik_data(precision, replicated_data) + log_lik_prior(precision)
return _log_lik
ধাপ 4: নমুনা
ঠিক আছে, নমুনা করার সময়! জিনিসগুলি সহজ রাখতে, আমরা শুধুমাত্র 1টি চেইন ব্যবহার করব এবং আমরা পরিচয় ম্যাট্রিক্সটিকে শুরুর বিন্দু হিসাবে ব্যবহার করব। আমরা পরে আরো সাবধানে কাজ করব.
আবার, এটি কাজ করতে যাচ্ছে না - আমরা একটি ব্যতিক্রম পাব।
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.expand_dims(tf.eye(2), axis=0)
# Use expand_dims because we want to pass in a tensor of starting values
log_lik_fn = get_log_lik(my_data, n_chains=1)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
return states
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
Cholesky decomposition was not successful. The input might not be valid.
[[{ {node mcmc_sample_chain/trace_scan/while/body/_79/smart_for_loop/while/body/_371/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_537/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/StatefulPartitionedCall/Cholesky} }]] [Op:__inference_sample_2849]
Function call stack:
sample
...
Function call stack:
sample
সমস্যা শনাক্তকরণ
InvalidArgumentError (see above for traceback): Cholesky decomposition was not successful. The input might not be valid. যে সুপার সহায়ক নয়. আসুন দেখি আমরা কি ঘটেছে সে সম্পর্কে আরও জানতে পারি কিনা।
- আমরা প্রতিটি ধাপের জন্য প্যারামিটারগুলি প্রিন্ট আউট করব যাতে আমরা দেখতে পারি যে জিনিসগুলি ব্যর্থ হয়
- নির্দিষ্ট সমস্যা থেকে রক্ষা পেতে আমরা কিছু দাবি যোগ করব।
দাবী করা কঠিন কারণ সেগুলি TensorFlow অপারেশন, এবং আমাদের খেয়াল রাখতে হবে যে সেগুলি কার্যকর হয় এবং গ্রাফ থেকে অপ্টিমাইজ না হয়৷ এটা তোলে এর মূল্য পড়া এই ওভারভিউ TensorFlow ডিবাগিং এর যদি মেমরি গবেষকেরা সাথে পরিচিত না হয়। আপনি স্পষ্টভাবে ব্যবহার চালানো গবেষকেরা জোর করতে পারেন tf.control_dependencies (নিচের কোড মন্তব্য দেখুন)।
TensorFlow এর নেটিভ Print ফাংশন গবেষকেরা হিসাবে একই আচরণ আছে - এটা একটি অপারেশন, আর আপনি তা নিশ্চিত করতে executes কিছু যত্ন নেওয়া দরকার। Print যখন আমরা একটি নোটবুক এ কাজ করছেন অতিরিক্ত মাথাব্যাথা কারণ: তার আউটপুট পাঠানো হয় stderr , এবং stderr কক্ষে প্রদর্শন করা হয় না। আমরা এখানে একটি কৌতুক ব্যবহার করব: ব্যবহারের পরিবর্তে tf.Print , আমরা মাধ্যমে আমাদের নিজস্ব TensorFlow মুদ্রণের অপারেশনের তৈরি করব tf.pyfunc । দাবী হিসাবে, আমাদের নিশ্চিত করতে হবে যে আমাদের পদ্ধতি কার্যকর হয়।
def get_log_lik_verbose(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
def _log_lik(precisions):
# An internal method we'll make into a TensorFlow operation via tf.py_func
def _print_precisions(precisions):
print('precisions:\n', precisions)
return False # operations must return something!
# Turn our method into a TensorFlow operation
print_op = tf.compat.v1.py_func(_print_precisions, [precisions], tf.bool)
# Assertions are also operations, and some care needs to be taken to ensure
# that they're executed
assert_op = tf.assert_equal(
precisions, tf.linalg.matrix_transpose(precisions),
message='not symmetrical', summarize=4, name='symmetry_check')
# The control_dependencies statement forces its arguments to be executed
# before subsequent operations
with tf.control_dependencies([print_op, assert_op]):
return (log_lik_data(precisions, replicated_data) +
log_lik_prior(precisions))
return _log_lik
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.eye(2)[tf.newaxis, ...]
log_lik_fn = get_log_lik_verbose(my_data)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[ 0.24315196 -0.2761638 ]
[-0.33882257 0.8622 ]]]
assertion failed: [not symmetrical] [Condition x == y did not hold element-wise:] [x (leapfrog_integrate_one_step/add:0) = ] [[[0.243151963 -0.276163787][-0.338822573 0.8622]]] [y (leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/matrix_transpose/transpose:0) = ] [[[0.243151963 -0.338822573][-0.276163787 0.8622]]]
[[{ {node mcmc_sample_chain/trace_scan/while/body/_96/smart_for_loop/while/body/_381/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_503/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/symmetry_check_1/Assert/AssertGuard/else/_577/Assert} }]] [Op:__inference_sample_4837]
Function call stack:
sample
...
Function call stack:
sample
কেন এই ব্যর্থ হয়
স্যাম্পলার চেষ্টা করে এমন প্রথম নতুন প্যারামিটার মান হল একটি অপ্রতিসম ম্যাট্রিক্স। এটি চোলেস্কি পচনকে ব্যর্থ করে দেয়, যেহেতু এটি শুধুমাত্র প্রতিসম (এবং ইতিবাচক নির্দিষ্ট) ম্যাট্রিক্সের জন্য সংজ্ঞায়িত করা হয়েছে।
এখানে সমস্যা হল যে আমাদের আগ্রহের প্যারামিটার হল একটি নির্ভুল ম্যাট্রিক্স, এবং নির্ভুল ম্যাট্রিক্স অবশ্যই বাস্তব, প্রতিসম, এবং ইতিবাচক সুনির্দিষ্ট হতে হবে। নমুনাকারী এই সীমাবদ্ধতা সম্পর্কে কিছুই জানেন না (সম্ভবত গ্রেডিয়েন্টের মাধ্যমে ছাড়া), তাই এটি সম্পূর্ণভাবে সম্ভব যে নমুনাকারী একটি অবৈধ মান প্রস্তাব করবে, যা একটি ব্যতিক্রমের দিকে পরিচালিত করবে, বিশেষ করে যদি ধাপের আকার বড় হয়।
হ্যামিলটোনিয়ান মন্টে কার্লো স্যাম্পলারের সাহায্যে, আমরা খুব ছোট ধাপের আকার ব্যবহার করে সমস্যাটির চারপাশে কাজ করতে সক্ষম হতে পারি, যেহেতু গ্রেডিয়েন্টের প্যারামিটারগুলিকে অবৈধ অঞ্চল থেকে দূরে রাখা উচিত, কিন্তু ছোট ধাপের মাপ মানে ধীর অভিসারন। মেট্রোপলিস-হেস্টিংস স্যাম্পলারের সাথে, যে গ্রেডিয়েন্ট সম্পর্কে কিছুই জানে না, আমরা ধ্বংস হয়ে গেছি।
সংস্করণ 2: অনিয়ন্ত্রিত পরামিতিগুলিতে পুনরায় প্যারামিটারাইজিং
উপরের সমস্যাটির একটি সরল সমাধান রয়েছে: আমরা আমাদের মডেলটিকে পুনরায় প্যারামিটারাইজ করতে পারি যাতে নতুন প্যারামিটারে আর এই সীমাবদ্ধতা থাকে না। TFP টুলগুলির একটি দরকারী সেট প্রদান করে - বাইজেক্টর - এটি করার জন্য।
বাইজেক্টর দিয়ে পুনরায় পরিমাপকরণ
আমাদের নির্ভুলতা ম্যাট্রিক্স বাস্তব এবং প্রতিসম হতে হবে; আমরা একটি বিকল্প প্যারামিটারাইজেশন চাই যাতে এই সীমাবদ্ধতা নেই। একটি প্রারম্ভিক বিন্দু হল স্পষ্টতা ম্যাট্রিক্সের একটি চোলেস্কি ফ্যাক্টরাইজেশন। চোলেস্কি ফ্যাক্টরগুলি এখনও সীমাবদ্ধ - তারা নিম্ন ত্রিভুজাকার, এবং তাদের তির্যক উপাদানগুলি অবশ্যই ধনাত্মক হতে হবে। যাইহোক, যদি আমরা চোলেস্কি ফ্যাক্টরের কর্ণগুলির লগ নিই, লগগুলি আর ধনাত্মক হওয়ার জন্য সীমাবদ্ধ থাকে না, এবং তারপরে যদি আমরা নীচের ত্রিভুজাকার অংশটিকে 1-D ভেক্টরে সমতল করি, তাহলে আমাদের আর নীচের ত্রিভুজাকার সীমাবদ্ধতা থাকবে না। . আমাদের ক্ষেত্রে ফলাফল হবে একটি দৈর্ঘ্য 3 ভেক্টর কোন বাধা ছাড়াই।
( স্ট্যান ম্যানুয়াল রূপান্তরের ব্যবহার পরামিতি উপর সীমাবদ্ধতা বিভিন্ন ধরনের অপসারণ করা যায় একটি দুর্দান্ত অধ্যায় আছে।)
এই রিপ্যারামিটারাইজেশন আমাদের ডেটা লগ সম্ভাবনা ফাংশনের উপর সামান্য প্রভাব ফেলে - আমাদের কেবল আমাদের রূপান্তরকে উল্টাতে হবে যাতে আমরা নির্ভুল ম্যাট্রিক্স ফিরে পেতে পারি - তবে পূর্বের উপর প্রভাব আরও জটিল। আমরা নির্দিষ্ট করেছি যে প্রদত্ত নির্ভুল ম্যাট্রিক্সের সম্ভাব্যতা উইশার্ট বিতরণ দ্বারা দেওয়া হয়; আমাদের রূপান্তরিত ম্যাট্রিক্সের সম্ভাবনা কত?
রিকল যে যদি আমরা একটি একঘেয়ে ফাংশন প্রয়োগ \(g\) একটি 1-ডি দৈব চলক করার \(X\), \(Y = g(X)\)জন্য ঘনত্ব \(Y\) দেওয়া হয়
\[ f_Y(y) = | \frac{d}{dy}(g^{-1}(y)) | f_X(g^{-1}(y)) \]
ডেরিভেটিভ \(g^{-1}\) মেয়াদ উপায় যে জন্য অ্যাকাউন্ট \(g\) স্থানীয় ভলিউম পরিবর্তন। উচ্চ মাত্রিক র্যান্ডম ভেরিয়েবল জন্য, সংশোধনমূলক ফ্যাক্টর এর Jacobian এর নির্ধারক পরম মান \(g^{-1}\) (দেখুন এখানে )।
আমাদের লগ পূর্ব সম্ভাবনা ফাংশনে বিপরীত রূপান্তরের একটি জ্যাকোবিয়ান যোগ করতে হবে। আনন্দের বিষয় হল, TFP এর Bijector বর্গ আমাদের জন্য এই যত্ন নিতে পারেন।
Bijector বর্গ বিপরীত, মসৃণ সম্ভাব্যতা ঘনত্ব ফাংশন ভেরিয়েবল পরিবর্তন করার জন্য ব্যবহৃত ফাংশন প্রতিনিধিত্ব করতে ব্যবহৃত হয়। Bijectors সমস্ত একটি আছে forward() পদ্ধতি যা সঞ্চালিত একটি রুপান্তর, একটি inverse() পদ্ধতি যা inverts এটা, এবং forward_log_det_jacobian() এবং inverse_log_det_jacobian() পদ্ধতি Jacobian সংশোধন দরকার, যখন আমরা একটি পিডিএফ reparaterize প্রদান।
TFP দরকারী bijectors যে আমরা মাধ্যমে রচনা মাধ্যমে একত্রিত করতে পারেন একটি সংগ্রহ প্রদান করে Chain অপারেটর বেশ জটিল রূপান্তরগুলির গঠনের। আমাদের ক্ষেত্রে, আমরা নিম্নলিখিত 3টি বিজেক্টর রচনা করব (চেইনের ক্রিয়াকলাপগুলি ডান থেকে বামে সঞ্চালিত হয়):
- আমাদের রূপান্তরের প্রথম ধাপ হল নির্ভুল ম্যাট্রিক্সে একটি চোলেস্কি ফ্যাক্টরাইজেশন করা। এর জন্য একটি বিজেক্টর ক্লাস নেই; তবে
CholeskyOuterProductbijector 2 Cholesky কারণের পণ্য লাগে। আমরা অপারেশন ব্যবহারের বিপরীত ব্যবহার করতে পারেনInvertঅপারেটর। - পরবর্তী ধাপ হল চোলেস্কি ফ্যাক্টরের তির্যক উপাদানগুলির লগ নেওয়া। আমরা মাধ্যমে এই কাজ করা সম্ভব
TransformDiagonalbijector এবং বিপরীতExpbijector। - অবশেষে আমরা একটি ভেক্টর বিপরীত ব্যবহার করে ম্যাট্রিক্স নিচের ত্রিদলীয় অংশ চেপ্টা
FillTriangularbijector।
# Our transform has 3 stages that we chain together via composition:
precision_to_unconstrained = tfb.Chain([
# step 3: flatten the lower triangular portion of the matrix
tfb.Invert(tfb.FillTriangular(validate_args=VALIDATE_ARGS)),
# step 2: take the log of the diagonals
tfb.TransformDiagonal(tfb.Invert(tfb.Exp(validate_args=VALIDATE_ARGS))),
# step 1: decompose the precision matrix into its Cholesky factors
tfb.Invert(tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS)),
])
# sanity checks
m = tf.constant([[1., 2.], [2., 8.]])
m_fwd = precision_to_unconstrained.forward(m)
m_inv = precision_to_unconstrained.inverse(m_fwd)
# bijectors handle tensors of values, too!
m2 = tf.stack([m, tf.eye(2)])
m2_fwd = precision_to_unconstrained.forward(m2)
m2_inv = precision_to_unconstrained.inverse(m2_fwd)
print('single input:')
print('m:\n', m.numpy())
print('precision_to_unconstrained(m):\n', m_fwd.numpy())
print('inverse(precision_to_unconstrained(m)):\n', m_inv.numpy())
print()
print('tensor of inputs:')
print('m2:\n', m2.numpy())
print('precision_to_unconstrained(m2):\n', m2_fwd.numpy())
print('inverse(precision_to_unconstrained(m2)):\n', m2_inv.numpy())
single input: m: [[1. 2.] [2. 8.]] precision_to_unconstrained(m): [0.6931472 2. 0. ] inverse(precision_to_unconstrained(m)): [[1. 2.] [2. 8.]] tensor of inputs: m2: [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]] precision_to_unconstrained(m2): [[0.6931472 2. 0. ] [0. 0. 0. ]] inverse(precision_to_unconstrained(m2)): [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]]
TransformedDistribution ক্লাসে প্রয়োজনীয় Jacobian সংশোধন একটি বিতরণ করার জন্য একটি bijector আবেদন এবং উপার্জন প্রক্রিয়া স্বয়ংক্রিয়রূপে log_prob() আমাদের নতুন পূর্বে পরিণত হয়:
def log_lik_prior_transformed(transformed_precisions):
rv_precision = tfd.TransformedDistribution(
tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS),
bijector=precision_to_unconstrained,
validate_args=VALIDATE_ARGS)
return rv_precision.log_prob(transformed_precisions)
# Check against the numpy implementation. Note that when comparing, we need
# to add in the Jacobian correction.
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_prior_transformed(transformed_precisions).numpy()
corrections = precision_to_unconstrained.inverse_log_det_jacobian(
transformed_precisions, event_ndims=1).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow: -0.84889317 1 numpy: -7.305657151741624 tensorflow: -7.305659
আমাদের কেবলমাত্র আমাদের ডেটা লগ সম্ভাবনার জন্য রূপান্তরটি উল্টাতে হবে:
precision = precision_to_unconstrained.inverse(transformed_precision)
যেহেতু আমরা প্রকৃতপক্ষে স্পষ্টতা ম্যাট্রিক্সের চোলেস্কি ফ্যাক্টরাইজেশন চাই, তাই এখানে শুধুমাত্র একটি আংশিক বিপরীত কাজ করা আরও কার্যকর হবে। যাইহোক, আমরা পরের জন্য অপ্টিমাইজেশন ছেড়ে দেব এবং পাঠকের জন্য একটি অনুশীলন হিসাবে আংশিক উল্টোটা ছেড়ে দেব।
def log_lik_data_transformed(transformed_precisions, replicated_data):
# We recover the precision matrix by inverting our bijector. This is
# inefficient since we really want the Cholesky decomposition of the
# precision matrix, and the bijector has that in hand during the inversion,
# but we'll worry about efficiency later.
n = tf.shape(transformed_precisions)[0]
precisions = precision_to_unconstrained.inverse(transformed_precisions)
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# sanity check
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_data_transformed(
transformed_precisions, replicated_data).numpy()
for i in range(precisions.shape[0]):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
আবার আমরা আমাদের নতুন ফাংশনগুলিকে বন্ধ করে রাখি।
def get_log_lik_transformed(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_transformed(transformed_precisions):
return (log_lik_data_transformed(transformed_precisions, replicated_data) +
log_lik_prior_transformed(transformed_precisions))
return _log_lik_transformed
# make sure everything runs
log_lik_fn = get_log_lik_transformed(my_data)
m = tf.eye(2)[tf.newaxis, ...]
lik = log_lik_fn(precision_to_unconstrained.forward(m)).numpy()
print(lik)
[-431.5611]
স্যাম্পলিং
এখন যেহেতু অবৈধ প্যারামিটার মানের কারণে আমাদের স্যাম্পলার উড়িয়ে নিয়ে চিন্তা করতে হবে না, আসুন কিছু বাস্তব নমুনা তৈরি করি।
নমুনা আমাদের পরামিতিগুলির অনিয়ন্ত্রিত সংস্করণের সাথে কাজ করে, তাই আমাদের প্রাথমিক মানটিকে এর অনিয়ন্ত্রিত সংস্করণে রূপান্তর করতে হবে। আমরা যে নমুনাগুলি তৈরি করি সেগুলিও তাদের অনিয়ন্ত্রিত আকারে থাকবে, তাই আমাদের সেগুলিকে আবার রূপান্তর করতে হবে। বিজেক্টর ভেক্টরাইজড, তাই এটি করা সহজ।
# We'll choose a proper random initial value this time
np.random.seed(123)
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_value = initial_value_cholesky.dot(
initial_value_cholesky.T)[np.newaxis, ...]
# The sampler works with unconstrained values, so we'll transform our initial
# value
initial_value_transformed = precision_to_unconstrained.forward(
initial_value).numpy()
# Sample!
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data, n_chains=1)
num_results = 1000
num_burnin_steps = 1000
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
initial_value_transformed,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=lambda _, pkr: pkr.is_accepted,
seed=123)
# transform samples back to their constrained form
precision_samples = [precision_to_unconstrained.inverse(s) for s in states]
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
আসুন বিশ্লেষণাত্মক পোস্টেরিয়র গড়ের সাথে আমাদের নমুনার আউটপুটের গড় তুলনা করি!
print('True posterior mean:\n', posterior_mean)
print('Sample mean:\n', np.mean(np.reshape(precision_samples, [-1, 2, 2]), axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Sample mean: [[ 1.4315274 -0.25587553] [-0.25587553 0.5740424 ]]
আমরা পথ বন্ধ! এর কারণ খুঁজে বের করা যাক. প্রথমে আমাদের নমুনা তাকান.
np.reshape(precision_samples, [-1, 2, 2])
array([[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
...,
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]]], dtype=float32)
উহ ওহ - মনে হচ্ছে তাদের সকলেরই একই মান আছে। এর কারণ খুঁজে বের করা যাক.
kernel_results_ পরিবর্তনশীল একটি নামাঙ্কিত tuple প্রতিটি রাষ্ট্র এ টাঙানো নকশা-বোনা সম্পর্কে তথ্য দেয়। is_accepted ফিল্ড কী এখানে।
# Look at the acceptance for the last 100 samples
print(np.squeeze(is_accepted)[-100:])
print('Fraction of samples accepted:', np.mean(np.squeeze(is_accepted)))
[False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False] Fraction of samples accepted: 0.0
আমাদের সব নমুনা প্রত্যাখ্যান করা হয়েছে! সম্ভবত আমাদের পদক্ষেপের আকার খুব বড় ছিল। আমি পছন্দ stepsize=0.1 বিশুদ্ধরূপে ইচ্ছামত।
সংস্করণ 3: একটি অভিযোজিত ধাপের আকার সহ নমুনা
যেহেতু ধাপের আকারের আমার নির্বিচারে পছন্দের সাথে নমুনা নেওয়া ব্যর্থ হয়েছে, আমাদের কাছে কয়েকটি বিষয়সূচি আইটেম রয়েছে:
- একটি অভিযোজিত পদক্ষেপ আকার বাস্তবায়ন, এবং
- কিছু কনভারজেন্স চেক সঞ্চালন.
সেখানে কিছু চমৎকার নমুনা কোড tensorflow_probability/python/mcmc/hmc.py অভিযোজিত পদক্ষেপ মাপ বাস্তবায়ন জন্য। আমি নীচে এটি অভিযোজিত করেছি.
উল্লেখ্য পৃথক আছে যে sess.run() প্রতিটি ধাপের জন্য বিবৃতি। এটি ডিবাগিংয়ের জন্য সত্যিই সহায়ক, কারণ এটি আমাদের প্রয়োজন হলে সহজেই কিছু প্রতি-পদক্ষেপ ডায়াগনস্টিক যোগ করতে দেয়। উদাহরণস্বরূপ, আমরা ক্রমবর্ধমান অগ্রগতি, প্রতিটি ধাপে সময় ইত্যাদি দেখাতে পারি।
টিপ: আপনার স্যাম্পলিং আপ জগাখিচুড়ি এক দৃশ্যত সাধারণ উপায় লুপ আপনার গ্রাফ হত্তয়া আছে। (সেশন চালানোর আগে গ্রাফটি চূড়ান্ত করার কারণ হল এই ধরনের সমস্যাগুলি প্রতিরোধ করা।) আপনি যদি finalize() ব্যবহার না করে থাকেন তবে, একটি দরকারী ডিবাগিং চেক যদি আপনার কোড ক্রল করতে ধীর হয়ে যায় কিনা তা হল গ্রাফটি প্রিন্ট করা। মাধ্যমে প্রতিটি পদক্ষেপ এ আকার len(mygraph.get_operations()) - যদি দৈর্ঘ্য বৃদ্ধি, আপনি সম্ভবত কিছু খারাপ করছেন।
আমরা এখানে 3টি স্বাধীন চেইন চালাতে যাচ্ছি। চেইনের মধ্যে কিছু তুলনা করা আমাদেরকে কনভারজেন্স পরীক্ষা করতে সাহায্য করবে।
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values = []
for i in range(N_CHAINS):
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_values.append(initial_value_cholesky.dot(initial_value_cholesky.T))
initial_values = np.stack(initial_values)
initial_values_transformed = precision_to_unconstrained.forward(
initial_values).numpy()
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=hmc,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values_transformed,
kernel=adapted_kernel,
trace_fn=lambda _, pkr: pkr.inner_results.is_accepted,
parallel_iterations=1)
# transform samples back to their constrained form
precision_samples = precision_to_unconstrained.inverse(states)
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
একটি দ্রুত পরীক্ষা: আমাদের নমুনা নেওয়ার সময় আমাদের গ্রহণযোগ্যতার হার আমাদের লক্ষ্য 0.651 এর কাছাকাছি।
print(np.mean(is_accepted))
0.6190666666666667
আরও ভাল, আমাদের নমুনা গড় এবং মানক বিচ্যুতি বিশ্লেষণাত্মক সমাধান থেকে আমরা যা আশা করি তার কাছাকাছি।
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96426415 -1.6519215 ] [-1.6519215 3.8614824 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13622096 0.25235635] [0.25235635 0.5394968 ]]
অভিসার জন্য পরীক্ষা করা হচ্ছে
সাধারণভাবে আমাদের কাছে পরীক্ষা করার জন্য একটি বিশ্লেষণাত্মক সমাধান থাকবে না, তাই আমাদের নিশ্চিত করতে হবে যে নমুনাটি একত্রিত হয়েছে। এক স্ট্যানডার্ড চেক Gelman-রুবিন হয় \(\hat{R}\) পরিসংখ্যাত, যা একাধিক স্যাম্পলিং চেইন প্রয়োজন। \(\hat{R}\) ব্যবস্থা যা ভ্যারিয়েন্স (মানে) চেইন মধ্যে থেকে ডিগ্রী অতিক্রম করে যদি চেইন অভিন্নরুপে বিতরণ করা হয়েছে এক আশা কি। এর মান \(\hat{R}\) 1 পাসে আনুমানিক অভিসৃতি ইঙ্গিত ব্যবহার করা হয়। দেখুন উৎস বিস্তারিত জানার জন্য।
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0038308 1.0005717] [1.0005717 1.0006068]]
মডেল সমালোচনা
যদি আমাদের কাছে একটি বিশ্লেষণাত্মক সমাধান না থাকে তবে এটি কিছু বাস্তব মডেল সমালোচনা করার সময় হবে।
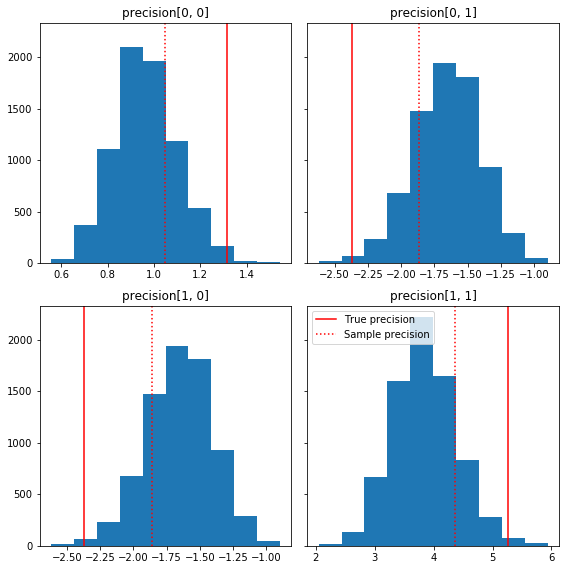
এখানে আমাদের স্থল সত্যের সাথে সম্পর্কিত নমুনা উপাদানগুলির কয়েকটি দ্রুত হিস্টোগ্রাম রয়েছে (লাল রঙে)। নোট করুন যে নমুনাগুলি পূর্বের পরিচয় ম্যাট্রিক্সের দিকে নমুনা নির্ভুলতা ম্যাট্রিক্স মান থেকে সঙ্কুচিত হয়েছে।
fig, axes = plt.subplots(2, 2, sharey=True)
fig.set_size_inches(8, 8)
for i in range(2):
for j in range(2):
ax = axes[i, j]
ax.hist(precision_samples_reshaped[:, i, j])
ax.axvline(true_precision[i, j], color='red',
label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':',
label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.tight_layout()
plt.legend()
plt.show()
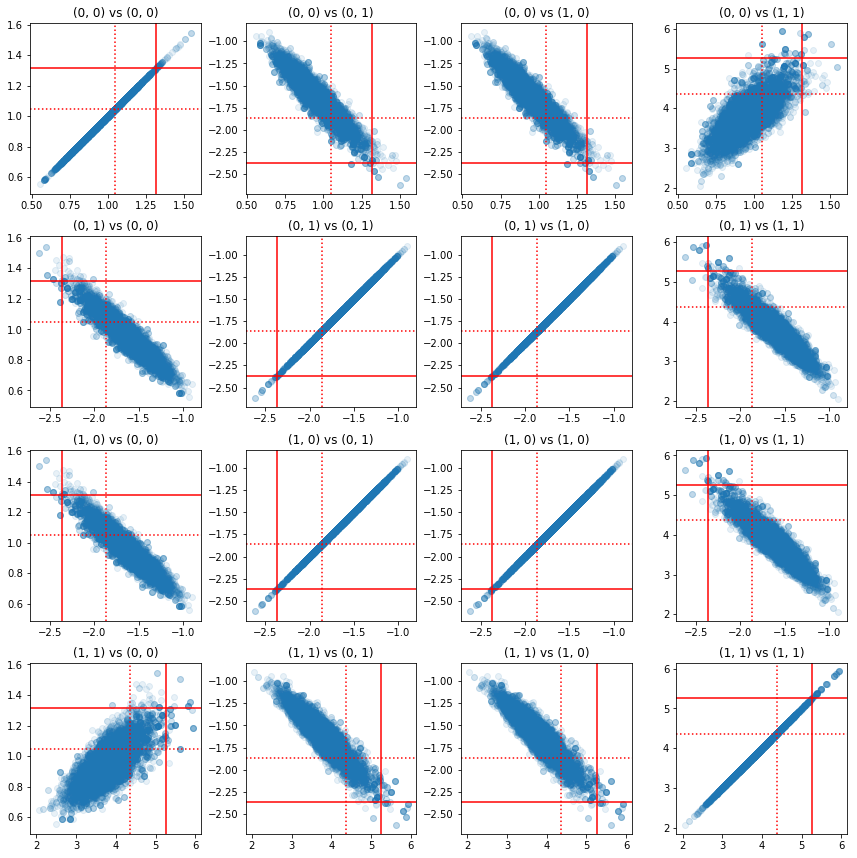
সূক্ষ্ম উপাদানগুলির জোড়ার কিছু বিক্ষিপ্ত প্লট দেখায় যে পোস্টেরিয়রের পারস্পরিক সম্পর্ক কাঠামোর কারণে, প্রকৃত উত্তরের মানগুলি উপরের প্রান্তিক থেকে প্রদর্শিত হওয়ার মতো অসম্ভাব্য নয়।
fig, axes = plt.subplots(4, 4)
fig.set_size_inches(12, 12)
for i1 in range(2):
for j1 in range(2):
index1 = 2 * i1 + j1
for i2 in range(2):
for j2 in range(2):
index2 = 2 * i2 + j2
ax = axes[index1, index2]
ax.scatter(precision_samples_reshaped[:, i1, j1],
precision_samples_reshaped[:, i2, j2], alpha=0.1)
ax.axvline(true_precision[i1, j1], color='red')
ax.axhline(true_precision[i2, j2], color='red')
ax.axvline(sample_precision[i1, j1], color='red', linestyle=':')
ax.axhline(sample_precision[i2, j2], color='red', linestyle=':')
ax.set_title('(%d, %d) vs (%d, %d)' % (i1, j1, i2, j2))
plt.tight_layout()
plt.show()
সংস্করণ 4: সীমাবদ্ধ পরামিতিগুলির সহজ নমুনা
বিজেক্টররা নির্ভুল ম্যাট্রিক্সের নমুনাকে সহজবোধ্য করে তোলে, কিন্তু সীমাহীন উপস্থাপনা থেকে এবং এর থেকে প্রচুর পরিমাণে ম্যানুয়াল রূপান্তর করা হয়েছিল। একটি সহজ উপায় আছে!
রূপান্তরিত ট্রানজিশন কার্নেল
TransformedTransitionKernel এই প্রক্রিয়া সহজসাধ্য। এটি আপনার নমুনাকে মোড়ানো এবং সমস্ত রূপান্তর পরিচালনা করে। এটি একটি যুক্তি হিসাবে বাইজেক্টরের একটি তালিকা নেয় যা সীমাবদ্ধ প্যারামিটার মানগুলিকে সীমাবদ্ধগুলির সাথে মানচিত্র করে। তাই আমরা এখানে বিপরীত প্রয়োজন precision_to_unconstrained bijector আমরা উপরোক্ত ব্যবহৃত। আমরা শুধু ব্যবহার করতে পারে tfb.Invert(precision_to_unconstrained) , কিন্তু যে inverses এর inverses পাড়িয়া জড়িত হবে (TensorFlow প্রক্রিয়া সহজ করার জন্য স্মার্ট যথেষ্ট নয় tf.Invert(tf.Invert()) থেকে tf.Identity()) , তাই এর পরিবর্তে আমরা 'শুধু একটি নতুন বিজেক্টর লিখব।
সীমাবদ্ধ বিজেক্টর
# The bijector we need for the TransformedTransitionKernel is the inverse of
# the one we used above
unconstrained_to_precision = tfb.Chain([
# step 3: take the product of Cholesky factors
tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS),
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: map a vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# quick sanity check
m = [[1., 2.], [2., 8.]]
m_inv = unconstrained_to_precision.inverse(m).numpy()
m_fwd = unconstrained_to_precision.forward(m_inv).numpy()
print('m:\n', m)
print('unconstrained_to_precision.inverse(m):\n', m_inv)
print('forward(unconstrained_to_precision.inverse(m)):\n', m_fwd)
m: [[1.0, 2.0], [2.0, 8.0]] unconstrained_to_precision.inverse(m): [0.6931472 2. 0. ] forward(unconstrained_to_precision.inverse(m)): [[1. 2.] [2. 8.]]
TransformedTransitionKernel দিয়ে স্যাম্পলিং
সঙ্গে TransformedTransitionKernel , আমরা আর আমাদের প্যারামিটার ম্যানুয়াল রূপান্তরের করতে হবে। আমাদের প্রাথমিক মান এবং আমাদের নমুনাগুলি সমস্ত নির্ভুল ম্যাট্রিক্স; আমাদের শুধু কার্নেলে আমাদের সীমাবদ্ধ বিজেক্টর(গুলি) পাস করতে হবে এবং এটি সমস্ত রূপান্তরের যত্ন নেয়।
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
return states
precision_samples = sample()
কনভারজেন্স পরীক্ষা করা হচ্ছে
\(\hat{R}\) অভিসৃতি চেক সৌন্দর্য ভাল!
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013582 1.0019467] [1.0019467 1.0011805]]
বিশ্লেষণাত্মক পোস্টেরিয়ার বিরুদ্ধে তুলনা
আবার এর বিশ্লেষণাত্মক পোস্টেরিয়ার বিরুদ্ধে চেক করা যাক.
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96687526 -1.6552585 ] [-1.6552585 3.867676 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329624 0.24913791] [0.24913791 0.53983927]]
অপ্টিমাইজেশান
এখন যেহেতু আমরা এন্ড-টু-এন্ড চলমান জিনিসগুলি পেয়েছি, আসুন আরও অপ্টিমাইজ করা সংস্করণ করি। এই উদাহরণের জন্য গতি খুব বেশি গুরুত্বপূর্ণ নয়, কিন্তু একবার ম্যাট্রিক্স বড় হয়ে গেলে, কয়েকটি অপ্টিমাইজেশন একটি বড় পার্থক্য তৈরি করবে।
একটি বড় গতির উন্নতি যা আমরা করতে পারি তা হল চোলেস্কি পচনের পরিপ্রেক্ষিতে পুনরায় প্যারামিটারাইজ করা। কারণ হল আমাদের ডেটা সম্ভাবনা ফাংশনের জন্য কোভেরিয়েন্স এবং নির্ভুলতা ম্যাট্রিক্স উভয়েরই প্রয়োজন। ম্যাট্রিক্স বিপর্যয় ব্যয়বহুল (হয়\(O(n^3)\) একটি জন্য \(n \times n\) ম্যাট্রিক্স), এবং যদি আমরা পারেন সহভেদাংক বা স্পষ্টতা ম্যাট্রিক্স পরিপ্রেক্ষিতে parameterize, আমরা অন্য পেতে একটি বিপর্যয় করতে হবে।
একটি অনুস্মারক হিসেবে একটি বাস্তব ইতিবাচক-নির্দিষ্ট, প্রতিসম ম্যাট্রিক্স \(M\) ফর্মের একটি পণ্য করা যায় পচে \(M = L L^T\) যেখানে ম্যাট্রিক্স \(L\) নিম্ন ত্রিকোণ হয় এবং ইতিবাচক কর্ণ হয়েছে। এর Cholesky পচানি দেওয়া \(M\), আমরা আরো দক্ষতার সঙ্গে উভয় পেতে পারেন \(M\) (ক কম গুণফল এবং একটি ঊর্ধ্ব ত্রিদলীয় ম্যাট্রিক্স) এবং \(M^{-1}\) (ব্যাক-প্রতিকল্পন মাধ্যমে)। চোলেস্কি ফ্যাক্টরাইজেশন নিজেই গণনা করা সস্তা নয়, তবে আমরা যদি চোলেস্কি ফ্যাক্টরগুলির পরিপ্রেক্ষিতে প্যারামিটারাইজ করি তবে আমাদের শুধুমাত্র প্রাথমিক প্যারামিটার মানগুলির চোলেক্সি ফ্যাক্টরাইজেশন গণনা করতে হবে।
কোভারিয়েন্স ম্যাট্রিক্সের চোলেস্কি পচন ব্যবহার করে
TFP বহুচলকীয় স্বাভাবিক বন্টন, একটি সংস্করণ রয়েছে MultivariateNormalTriL , যে সহভেদাংক ম্যাট্রিক্স Cholesky ফ্যাক্টর পরিপ্রেক্ষিতে স্থিতিমাপ করা হয়। সুতরাং আমরা যদি কোভেরিয়েন্স ম্যাট্রিক্সের চোলেস্কি ফ্যাক্টরের পরিপ্রেক্ষিতে প্যারামিটারাইজ করি, আমরা দক্ষতার সাথে ডেটা লগের সম্ভাবনা গণনা করতে পারি। চ্যালেঞ্জ হল একই দক্ষতার সাথে পূর্ববর্তী লগ সম্ভাবনা গণনা করা।
যদি আমাদের কাছে ইনভার্স উইশার্ট ডিস্ট্রিবিউশনের একটি সংস্করণ থাকে যা নমুনার চোলেস্কি ফ্যাক্টরগুলির সাথে কাজ করে, আমরা প্রস্তুত থাকতাম। হায়, আমরা না. (যদিও দলটি কোড দাখিলকে স্বাগত জানাবে!) একটি বিকল্প হিসাবে, আমরা উইশার্ট বিতরণের একটি সংস্করণ ব্যবহার করতে পারি যা নমুনার চোলেস্কি ফ্যাক্টরগুলির সাথে বাইজেক্টরের একটি চেইন সহ কাজ করে৷
এই মুহুর্তে, জিনিসগুলিকে সত্যিই দক্ষ করে তুলতে আমরা কয়েকটি স্টক বিজেক্টর মিস করছি, কিন্তু আমি এই প্রক্রিয়াটিকে একটি ব্যায়াম এবং TFP-এর বাইজেক্টরগুলির শক্তির একটি দরকারী চিত্র হিসাবে দেখাতে চাই৷
একটি উইশার্ট বিতরণ যা চোলেস্কি ফ্যাক্টরগুলির উপর কাজ করে
Wishart বন্টন একটি দরকারী পতাকা আছে, input_output_cholesky যে নির্দিষ্ট করে ইনপুট এবং আউটপুট ম্যাট্রিক্স Cholesky কারণের হওয়া উচিত। সম্পূর্ণ ম্যাট্রিক্সের চেয়ে চোলেস্কি ফ্যাক্টরগুলির সাথে কাজ করা আরও দক্ষ এবং সংখ্যাগতভাবে সুবিধাজনক, এই কারণেই এটি কাম্য। পতাকার শব্দার্থবিদ্যা সম্বন্ধে একটি গুরুত্বপূর্ণ পয়েন্ট: এটি শুধুমাত্র একটি ইঙ্গিত যে ইনপুট ও বন্টন আউটপুট প্রতিনিধিত্ব পরিবর্তন করা উচিত - এটি বন্টন, যা করার জন্য একটি Jacobian সংশোধন জড়িত করা হবে একটি পূর্ণ reparameterization নির্দেশ করে না log_prob() ফাংশন আমরা আসলে এই সম্পূর্ণ রিপ্যারামিটারাইজেশন করতে চাই, তাই আমরা আমাদের নিজস্ব ডিস্ট্রিবিউশন তৈরি করব।
# An optimized Wishart distribution that has been transformed to operate on
# Cholesky factors instead of full matrices. Note that we gain a modest
# additional speedup by specifying the Cholesky factor of the scale matrix
# (i.e. by passing in the scale_tril parameter instead of scale).
class CholeskyWishart(tfd.TransformedDistribution):
"""Wishart distribution reparameterized to use Cholesky factors."""
def __init__(self,
df,
scale_tril,
validate_args=False,
allow_nan_stats=True,
name='CholeskyWishart'):
# Wishart has a bunch of methods that we want to support but not
# implement. We'll subclass TransformedDistribution here to take care of
# those. We'll override the few for which speed is critical and implement
# them with a separate Wishart for which input_output_cholesky=True
super(CholeskyWishart, self).__init__(
distribution=tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=False,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()),
validate_args=validate_args,
name=name
)
# Here's the Cholesky distribution we'll use for log_prob() and sample()
self.cholesky = tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=True,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats)
def _log_prob(self, x):
return (self.cholesky.log_prob(x) +
self.bijector.inverse_log_det_jacobian(x, event_ndims=2))
def _sample_n(self, n, seed=None):
return self.cholesky._sample_n(n, seed)
# some checks
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
@tf.function(autograph=False)
def compute_log_prob(m):
w_transformed = tfd.TransformedDistribution(
tfd.WishartTriL(df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()))
w_optimized = CholeskyWishart(
df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY)
log_prob_transformed = w_transformed.log_prob(m)
log_prob_optimized = w_optimized.log_prob(m)
return log_prob_transformed, log_prob_optimized
for matrix in [np.eye(2, dtype=np.float32),
np.array([[1., 0.], [2., 8.]], dtype=np.float32)]:
log_prob_transformed, log_prob_optimized = [
t.numpy() for t in compute_log_prob(matrix)]
print('Transformed Wishart:', log_prob_transformed)
print('Optimized Wishart', log_prob_optimized)
Transformed Wishart: -0.84889317 Optimized Wishart -0.84889317 Transformed Wishart: -99.269455 Optimized Wishart -99.269455
একটি বিপরীত উইশার্ট বিতরণ তৈরি করা
আমরা আমাদের সহভেদাংক ম্যাট্রিক্স আছে \(C\) মধ্যে পচে \(C = L L^T\) যেখানে \(L\) নিম্ন ত্রিকোণ এবং একটি ইতিবাচক তির্যক হয়েছে। আমরা সম্ভাবনা জানতে চাই \(L\) দেওয়া যে \(C \sim W^{-1}(\nu, V)\) যেখানে \(W^{-1}\) বিশ্বকাপ বন্টন বিপরীত হয়।
বিপরীত বিশ্বকাপ বন্টন সম্পত্তি আছে যদি \(C \sim W^{-1}(\nu, V)\), তারপর স্পষ্টতা ম্যাট্রিক্স \(C^{-1} \sim W(\nu, V^{-1})\)। সুতরাং আমরা সম্ভাব্যতা পেতে পারেন \(L\) একটি মাধ্যমে TransformedDistribution যে বিশ্বকাপ বিতরণ এবং একটি bijector যে তার বিপরীত একটি Cholesky ফ্যাক্টর থেকে স্পষ্টতা ম্যাট্রিক্স Cholesky ফ্যাক্টর মানচিত্র পরামিতি হিসেবে গ্রহণ করে।
এর Cholesky ফ্যাক্টর থেকে পেতে একটি সহজবোধ্য (কিন্তু সুপার দক্ষ নয়) পথ \(C^{-1}\) করার \(L\) ব্যাক সমাধান করে Cholesky ফ্যাক্টর উল্টানো, তবে এই উল্টানো কারণের থেকে সহভেদাংক ম্যাট্রিক্স বিরচন, এবং তারপর একটি Cholesky গুণকনির্ণয় করছে .
এর Cholesky পচানি যাক \(C^{-1} = M M^T\)। \(M\) তাই আমরা ব্যবহার করে এটি invert করতে, নিম্ন ত্রিকোণ হয় MatrixInverseTriL bijector।
বিরচন \(C\) থেকে \(M^{-1}\) : একটি সামান্য চতুর হয় \(C = (M M^T)^{-1} = M^{-T}M^{-1} = M^{-T} (M^{-T})^T\)। \(M\) , নিম্ন ত্রিকোণ তাই \(M^{-1}\) এছাড়াও নিম্ন ত্রিকোণ হবে, এবং \(M^{-T}\) উপরের ত্রিদলীয় হতে হবে। CholeskyOuterProduct() bijector শুধুমাত্র, নিম্ন ত্রিকোণ ম্যাট্রিক্স সাথে কাজ করে তাই আমরা ব্যবহার করতে পারবেন না গঠনের \(C\) থেকে \(M^{-T}\)। আমাদের সমাধান হল বিজেক্টরের একটি চেইন যা একটি ম্যাট্রিক্সের সারি এবং কলামগুলিকে পারমিউট করে।
সৌভাগ্য যে এই যুক্তি মধ্যে encapsulated হয় CholeskyToInvCholesky bijector!
সব টুকরা একত্রিত
# verify that the bijector works
m = np.array([[1., 0.], [2., 8.]], dtype=np.float32)
c_inv = m.dot(m.T)
c = np.linalg.inv(c_inv)
c_chol = np.linalg.cholesky(c)
wishart_cholesky_to_iw_cholesky = tfb.CholeskyToInvCholesky()
w_fwd = wishart_cholesky_to_iw_cholesky.forward(m).numpy()
print('numpy =\n', c_chol)
print('bijector =\n', w_fwd)
numpy = [[ 1.0307764 0. ] [-0.03031695 0.12126781]] bijector = [[ 1.0307764 0. ] [-0.03031695 0.12126781]]
আমাদের চূড়ান্ত বিতরণ
চোলেস্কি ফ্যাক্টরগুলির উপর আমাদের ইনভার্স উইশার্ট কাজ করে নিম্নরূপ:
inverse_wishart_cholesky = tfd.TransformedDistribution(
distribution=CholeskyWishart(
df=PRIOR_DF,
scale_tril=np.linalg.cholesky(np.linalg.inv(PRIOR_SCALE))),
bijector=tfb.CholeskyToInvCholesky())
আমরা আমাদের ইনভার্স উইশার্ট পেয়েছি, কিন্তু এটি ধীরগতির কারণ আমাদেরকে বাইজেক্টরে একটি চোলেস্কি পচন করতে হবে। আসুন নির্ভুল ম্যাট্রিক্স প্যারামিটারাইজেশনে ফিরে আসি এবং অপ্টিমাইজেশনের জন্য আমরা সেখানে কী করতে পারি তা দেখি।
চূড়ান্ত(!) সংস্করণ: নির্ভুল ম্যাট্রিক্সের চোলেস্কি পচন ব্যবহার করে
একটি বিকল্প পদ্ধতি হল সঠিক ম্যাট্রিক্সের চোলেস্কি ফ্যাক্টর নিয়ে কাজ করা। এখানে পূর্বের সম্ভাবনা ফাংশনটি গণনা করা সহজ, কিন্তু ডেটা লগ সম্ভাবনা ফাংশনটি আরও কাজ করে কারণ TFP-এর মাল্টিভেরিয়েট নরমালের কোনও সংস্করণ নেই যা নির্ভুলতার দ্বারা প্যারামিটারাইজ করা হয়।
অপ্টিমাইজ করা আগের লগ সম্ভাবনা
আমরা ব্যবহার CholeskyWishart বন্টন আমরা উপরোক্ত নির্মিত পূর্বে গঠন করা।
# Our new prior.
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
def log_lik_prior_cholesky(precisions_cholesky):
rv_precision = CholeskyWishart(
df=PRIOR_DF,
scale_tril=PRIOR_SCALE_CHOLESKY,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions_cholesky)
# Check against the slower TF implementation and the NumPy implementation.
# Note that when comparing to NumPy, we need to add in the Jacobian correction.
precisions = [np.eye(2, dtype=np.float32),
true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
lik_tf = log_lik_prior_cholesky(precisions_cholesky).numpy()
lik_tf_slow = tfd.TransformedDistribution(
distribution=tfd.WishartTriL(
df=PRIOR_DF, scale_tril=tf.linalg.cholesky(PRIOR_SCALE)),
bijector=tfb.Invert(tfb.CholeskyOuterProduct())).log_prob(
precisions_cholesky).numpy()
corrections = tfb.Invert(tfb.CholeskyOuterProduct()).inverse_log_det_jacobian(
precisions_cholesky, event_ndims=2).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow slow:', lik_tf_slow[i])
print('tensorflow fast:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow slow: -0.84889317 tensorflow fast: -0.84889317 1 numpy: -7.442875031036973 tensorflow slow: -7.442877 tensorflow fast: -7.442876
অপ্টিমাইজ করা ডেটা লগ সম্ভাবনা
We can use TFP's bijectors to build our own version of the multivariate normal. Here is the key idea:
Suppose I have a column vector \(X\) whose elements are iid samples of \(N(0, 1)\). We have \(\text{mean}(X) = 0\) and \(\text{cov}(X) = I\)
Now let \(Y = A X + b\). We have \(\text{mean}(Y) = b\) and \(\text{cov}(Y) = A A^T\)
Hence we can make vectors with mean \(b\) and covariance \(C\) using the affine transform \(Ax+b\) to vectors of iid standard Normal samples provided \(A A^T = C\). The Cholesky decomposition of \(C\) has the desired property. However, there are other solutions.
Let \(P = C^{-1}\) and let the Cholesky decomposition of \(P\) be \(B\), ie \(B B^T = P\). Now
\(P^{-1} = (B B^T)^{-1} = B^{-T} B^{-1} = B^{-T} (B^{-T})^T\)
So another way to get our desired mean and covariance is to use the affine transform \(Y=B^{-T}X + b\).
Our approach (courtesy of this notebook ):
- Use
tfd.Independent()to combine a batch of 1-DNormalrandom variables into a single multi-dimensional random variable. Thereinterpreted_batch_ndimsparameter forIndependent()specifies the number of batch dimensions that should be reinterpreted as event dimensions. In our case we create a 1-D batch of length 2 that we transform into a 1-D event of length 2, soreinterpreted_batch_ndims=1. - Apply a bijector to add the desired covariance:
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky, adjoint=True)). Note that above we're multiplying our iid normal random variables by the transpose of the inverse of the Cholesky factor of the precision matrix \((B^{-T}X)\). Thetfb.Inverttakes care of inverting \(B\), and theadjoint=Trueflag performs the transpose. - Apply a bijector to add the desired offset:
tfb.Shift(shift=shift)Note that we have to do the shift as a separate step from the initial inverted affine transform because otherwise the inverted scale is applied to the shift (since the inverse of \(y=Ax+b\) is \(x=A^{-1}y - A^{-1}b\)).
class MVNPrecisionCholesky(tfd.TransformedDistribution):
"""Multivariate normal parameterized by loc and Cholesky precision matrix."""
def __init__(self, loc, precision_cholesky, name=None):
super(MVNPrecisionCholesky, self).__init__(
distribution=tfd.Independent(
tfd.Normal(loc=tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky,
adjoint=True)),
]),
name=name)
@tf.function(autograph=False)
def log_lik_data_cholesky(precisions_cholesky, replicated_data):
n = tf.shape(precisions_cholesky)[0] # number of precision matrices
rv_data = MVNPrecisionCholesky(
loc=tf.zeros([n, 2]),
precision_cholesky=precisions_cholesky)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# check against the numpy implementation
true_precision_cholesky = np.linalg.cholesky(true_precision)
precisions = [np.eye(2, dtype=np.float32), true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
n = precisions_cholesky.shape[0]
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
lik_tf = log_lik_data_cholesky(precisions_cholesky, replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.81824
Combined log likelihood function
Now we combine our prior and data log likelihood functions in a closure.
def get_log_lik_cholesky(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_cholesky(precisions_cholesky):
return (log_lik_data_cholesky(precisions_cholesky, replicated_data) +
log_lik_prior_cholesky(precisions_cholesky))
return _log_lik_cholesky
Constraining bijector
Our samples are constrained to be valid Cholesky factors, which means they must be lower triangular matrices with positive diagonals. The TransformedTransitionKernel needs a bijector that maps unconstrained tensors to/from tensors with our desired constraints. We've removed the Cholesky decomposition from the bijector's inverse, which speeds things up.
unconstrained_to_precision_cholesky = tfb.Chain([
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: expand the vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# some checks
inv = unconstrained_to_precision_cholesky.inverse(precisions_cholesky).numpy()
fwd = unconstrained_to_precision_cholesky.forward(inv).numpy()
print('precisions_cholesky:\n', precisions_cholesky)
print('\ninv:\n', inv)
print('\nfwd(inv):\n', fwd)
precisions_cholesky: [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]] inv: [[ 0.0000000e+00 0.0000000e+00 0.0000000e+00] [ 3.5762781e-07 -2.0647411e+00 1.3721828e-01]] fwd(inv): [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]]
Initial values
We generate a tensor of initial values. We're working with Cholesky factors, so we generate some Cholesky factor initial values.
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values_cholesky = []
for i in range(N_CHAINS):
initial_values_cholesky.append(np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32))
initial_values_cholesky = np.stack(initial_values_cholesky)
Sampling
We sample N_CHAINS chains using the TransformedTransitionKernel .
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_cholesky(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision_cholesky)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
samples = tf.linalg.matmul(states, states, transpose_b=True)
return samples
precision_samples = sample()
Convergence check
A quick convergence check looks good:
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013583 1.0019467] [1.0019467 1.0011804]]
Comparing results to the analytic posterior
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, newshape=[-1, 2, 2])
And again, the sample means and standard deviations match those of the analytic posterior.
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.9668749 -1.6552604] [-1.6552604 3.8676758]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329637 0.24913797] [0.24913797 0.53983945]]
Ok, all done! We've got our optimized sampler working.
