 عرض على TensorFlow.org عرض على TensorFlow.org |  تشغيل في Google Colab تشغيل في Google Colab |  عرض المصدر على جيثب عرض المصدر على جيثب |  تحميل دفتر تحميل دفتر |
لقد كتبت هذا المفكرة كدراسة حالة لتعلم احتمالية TensorFlow. المشكلة التي اخترت حلها هي تقدير مصفوفة التغاير لعينات من 2-D يعني 0 متغير عشوائي غاوسي. المشكلة لها ميزتان جميلتان:
- إذا استخدمنا معكوس Wishart pre للتباين المشترك (نهج مشترك) ، فإن المشكلة لها حل تحليلي ، حتى نتمكن من التحقق من نتائجنا.
- تتضمن المشكلة أخذ عينة من معلمة مقيدة ، مما يضيف بعض التعقيد المثير للاهتمام.
- الحل الأكثر وضوحًا ليس هو الحل الأسرع ، لذلك هناك بعض أعمال التحسين التي يجب القيام بها.
قررت أن أكتب تجربتي مع تقدمي. لقد استغرقت بعض الوقت لف رأسي حول النقاط الدقيقة في TFP ، لذلك يبدأ هذا الكمبيوتر الدفتري ببساطة إلى حد ما ثم يعمل تدريجياً على ميزات TFP الأكثر تعقيدًا. واجهت الكثير من المشاكل على طول الطريق ، وحاولت التقاط كل من العمليات التي ساعدتني في التعرف عليها والحلول التي وجدتها في النهاية. لقد حاولت أن تشمل الكثير من التفاصيل (بما في ذلك الكثير من الاختبارات للتأكد الخطوات الفردية المؤكد صحيحة).
لماذا نتعلم احتمالية TensorFlow؟
لقد وجدت أن احتمالية TensorFlow جذابة لمشروعي لعدة أسباب:
- تتيح لك احتمالية TensorFlow تطوير نماذج معقدة بشكل تفاعلي في جهاز كمبيوتر محمول. يمكنك تقسيم الكود إلى أجزاء صغيرة يمكنك اختبارها بشكل تفاعلي وباستخدام اختبارات الوحدة.
- بمجرد أن تصبح جاهزًا للتوسع ، يمكنك الاستفادة من جميع البنية التحتية المتوفرة لدينا لجعل TensorFlow يعمل على معالجات متعددة ومحسّنة على أجهزة متعددة.
- أخيرًا ، بينما أحب ستان حقًا ، أجد أنه من الصعب جدًا تصحيح الأخطاء. يجب أن تكتب كل كود النمذجة الخاص بك بلغة قائمة بذاتها تحتوي على عدد قليل جدًا من الأدوات التي تتيح لك النقر على التعليمات البرمجية الخاصة بك ، وفحص الحالات الوسيطة ، وما إلى ذلك.
الجانب السلبي هو أن احتمالية TensorFlow أحدث بكثير من Stan و PyMC3 ، لذا فإن التوثيق هو عمل قيد التقدم ، وهناك الكثير من الوظائف التي لم يتم بناؤها بعد. لحسن الحظ ، وجدت أن أساس TFP متين ، وقد تم تصميمه بطريقة معيارية تسمح للمرء بتوسيع وظائفه بشكل مباشر إلى حد ما. في هذا الكمبيوتر الدفتري ، بالإضافة إلى حل دراسة الحالة ، سأعرض بعض الطرق للشروع في تمديد TFP.
لمن هذا
أفترض أن القراء يأتون إلى هذا دفتر الملاحظات ببعض المتطلبات الأساسية المهمة. يجب:
- تعرف على أساسيات الاستدلال البايزي. (إذا لم تقم بذلك، وأول كتاب لطيف هو الإحصائية إعادة النظر )
- هل لديك بعض الألفة مع مكتبة أخذ العينات MCMC، مثل ستان / PyMC3 / البق
- لديهم فهم متين من نمباي (واحد مقدمة جيدة هو بيثون لتحليل البيانات )
- هل لديك ما لا يقل عن مرور الألفة مع TensorFlow ، ولكن ليس بالضرورة الخبرة. ( التعلم TensorFlow أمر جيد، ولكن وسائل التطور السريع TensorFlow أن معظم الكتب سيتم قليلا مؤرخة. ستانفورد CS20 بالطبع هي أيضا جيدة.)
المحاولة الأولى
هذه هي محاولتي الأولى لحل المشكلة. Spoiler: الحل الخاص بي لا يعمل ، وسيستغرق الأمر عدة محاولات لتصحيح الأمور! على الرغم من أن العملية تستغرق بعض الوقت ، إلا أن كل محاولة أدناه كانت مفيدة لتعلم جزء جديد من برنامج TFP.
ملاحظة واحدة: TFP لا يطبق حاليًا توزيع Wishart المعكوس (سنرى في النهاية كيفية تدوير Wishart المعكوس الخاص بنا) ، لذلك بدلاً من ذلك سأغير المشكلة إلى مشكلة تقدير مصفوفة دقيقة باستخدام Wishart مسبقًا.
import collections
import math
import os
import time
import numpy as np
import pandas as pd
import scipy
import scipy.stats
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
الخطوة 1: اجمع الملاحظات معًا
جميع بياناتي هنا تركيبية ، لذا سيبدو هذا أكثر تنظيمًا قليلاً من مثال من العالم الحقيقي. ومع ذلك ، لا يوجد سبب يمنعك من إنشاء بعض البيانات التركيبية الخاصة بك.
نصيحة: مرة واحدة كنت قد قررت على شكل النموذج الخاص بك، يمكنك اختيار بعض قيم المعلمات واستخدام النموذج الذي اخترته لتوليد بعض البيانات الاصطناعية. للتحقق من سلامة التنفيذ ، يمكنك بعد ذلك التحقق من أن تقديراتك تتضمن القيم الحقيقية للمعلمات التي اخترتها. لجعل دورة التصحيح / الاختبار أسرع ، يمكنك التفكير في إصدار مبسط من نموذجك (على سبيل المثال ، استخدم أبعادًا أقل أو عينات أقل).
تلميح: إنها أسهل للعمل مع الملاحظات الخاصة بك كما صفائف نمباي. أحد الأشياء المهمة التي يجب ملاحظتها هو أن NumPy يستخدم بشكل افتراضي float64 ، بينما يستخدم TensorFlow افتراضيًا float32.
بشكل عام ، تريد عمليات TensorFlow أن يكون لجميع الوسائط نفس النوع ، وعليك أن تقوم بنقل البيانات الصريحة إلى أنواع التغيير. إذا كنت تستخدم ملاحظات float64 ، فستحتاج إلى إضافة الكثير من عمليات الإرسال. في المقابل ، سيهتم NumPy بالإرسال تلقائيًا. وبالتالي، فمن الأسهل بكثير لتحويل البيانات نمباي الخاص بك إلى float32 مما هو عليه لإجبار TensorFlow الاستخدام float64.
اختر بعض قيم المعلمات
# We're assuming 2-D data with a known true mean of (0, 0)
true_mean = np.zeros([2], dtype=np.float32)
# We'll make the 2 coordinates correlated
true_cor = np.array([[1.0, 0.9], [0.9, 1.0]], dtype=np.float32)
# And we'll give the 2 coordinates different variances
true_var = np.array([4.0, 1.0], dtype=np.float32)
# Combine the variances and correlations into a covariance matrix
true_cov = np.expand_dims(np.sqrt(true_var), axis=1).dot(
np.expand_dims(np.sqrt(true_var), axis=1).T) * true_cor
# We'll be working with precision matrices, so we'll go ahead and compute the
# true precision matrix here
true_precision = np.linalg.inv(true_cov)
# Here's our resulting covariance matrix
print(true_cov)
# Verify that it's positive definite, since np.random.multivariate_normal
# complains about it not being positive definite for some reason.
# (Note that I'll be including a lot of sanity checking code in this notebook -
# it's a *huge* help for debugging)
print('eigenvalues: ', np.linalg.eigvals(true_cov))
[[4. 1.8] [1.8 1. ]] eigenvalues: [4.843075 0.15692513]
قم بتوليد بعض الملاحظات التركيبية
علما بأن TensorFlow احتمال يستخدم الاتفاقية أن البعد الأولي (ق) من البيانات الخاصة بك تمثل مؤشرات عينة، والبعد النهائي (ق) من البيانات الخاصة بك تمثل الأبعاد من العينات الخاصة بك.
هنا نريد 100 عينة، كل منها هو متجه طول 2. ونحن سوف تولد مجموعة my_data مع شكل (100، 2). my_data[i, :] هو \(i\)عشر عينة، وأنه هو متجه طول 2.
(تذكر لجعل my_data دينا نوع float32!)
# Set the seed so the results are reproducible.
np.random.seed(123)
# Now generate some observations of our random variable.
# (Note that I'm suppressing a bunch of spurious about the covariance matrix
# not being positive semidefinite via check_valid='ignore' because it really is
# positive definite!)
my_data = np.random.multivariate_normal(
mean=true_mean, cov=true_cov, size=100,
check_valid='ignore').astype(np.float32)
my_data.shape
(100, 2)
تحقق من صحة الملاحظات
أحد المصادر المحتملة للأخطاء هو إفساد بياناتك التركيبية! لنقم ببعض الفحوصات البسيطة.
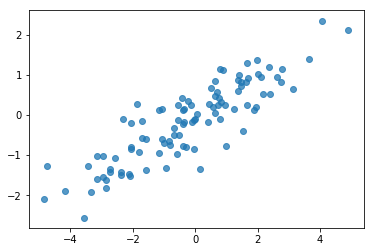
# Do a scatter plot of the observations to make sure they look like what we
# expect (higher variance on the x-axis, y values strongly correlated with x)
plt.scatter(my_data[:, 0], my_data[:, 1], alpha=0.75)
plt.show()
print('mean of observations:', np.mean(my_data, axis=0))
print('true mean:', true_mean)
mean of observations: [-0.24009615 -0.16638893] true mean: [0. 0.]
print('covariance of observations:\n', np.cov(my_data, rowvar=False))
print('true covariance:\n', true_cov)
covariance of observations: [[3.95307734 1.68718486] [1.68718486 0.94910269]] true covariance: [[4. 1.8] [1.8 1. ]]
حسنًا ، عيناتنا تبدو معقولة. الخطوة التالية.
الخطوة 2: تنفيذ دالة الاحتمال في NumPy
الشيء الرئيسي الذي سنحتاج إلى كتابته لأداء أخذ عينات MCMC في TF Probability هو دالة احتمالية في السجل. بشكل عام ، يعد كتابة TF أصعب قليلاً من كتابة NumPy ، لذلك أجد أنه من المفيد إجراء تنفيذ أولي في NumPy. انا ذاهب الى تقسيم دالة الإمكان إلى 2 قطعة، وهي وظيفة احتمال البيانات التي يتوافق مع \(P(data | parameters)\) ودالة الإمكان قبل أن يتوافق مع \(P(parameters)\).
لاحظ أن وظائف NumPy هذه لا يجب أن تكون محسّنة / متجهية فائقة لأن الهدف هو فقط إنشاء بعض القيم للاختبار. الصواب هو الاعتبار الرئيسي!
أولاً سنقوم بتنفيذ جزء احتمالية سجل البيانات. هذا واضح ومباشر. الشيء الوحيد الذي يجب تذكره هو أننا سنعمل باستخدام مصفوفات دقيقة ، لذلك سنقوم بتحديد المعلمات وفقًا لذلك.
def log_lik_data_numpy(precision, data):
# np.linalg.inv is a really inefficient way to get the covariance matrix, but
# remember we don't care about speed here
cov = np.linalg.inv(precision)
rv = scipy.stats.multivariate_normal(true_mean, cov)
return np.sum(rv.logpdf(data))
# test case: compute the log likelihood of the data given the true parameters
log_lik_data_numpy(true_precision, my_data)
-280.81822950593767
ونحن في طريقنا لاستخدام يشارت قبل لمصفوفة الدقة لأن هناك حلا التحليلي لاحق (انظر الجدول يكيبيديا مفيد للمقدمو الاديره المتقارن ).
و توزيع ويشارت ديه 2 المعلمات:
- عدد درجات الحرية (المسمى \(\nu\) في ويكيبيديا)
- مصفوفة على نطاق و(المسمى \(V\) في ويكيبيديا)
يعني لتوزيع يشارت مع المعلمات \(\nu, V\) هو \(E[W] = \nu V\)، والفرق هو \(\text{Var}(W_{ij}) = \nu(v_{ij}^2+v_{ii}v_{jj})\)
بعض الحدس مفيدا: يمكنك إنشاء نموذج يشارت عن طريق توليد \(\nu\) مستقلة توجه \(x_1 \ldots x_{\nu}\) من متغير عشوائي الطبيعي المتعدد مع الوسط 0 والتغاير \(V\) ومن ثم تشكيل مجموع \(W = \sum_{i=1}^{\nu} x_i x_i^T\).
إذا كنت إعادة مقياس عينات يشارت بقسمة لهم من قبل \(\nu\)، يمكنك الحصول على مصفوفة التغاير عينة من \(x_i\). هذا مصفوفة التغاير عينة يجب أن تميل نحو \(V\) كما \(\nu\) الزيادات. عندما \(\nu\) صغيرة، وهناك الكثير من الاختلاف في مصفوفة التغاير عينة، قيم صغيرة جدا من \(\nu\) تتوافق مع مقدمو الاديره أضعف وقيم كبيرة من \(\nu\) تتوافق مع مقدمو الاديره أقوى. علما بأن \(\nu\) يجب أن تكون على الأقل كبيرة مثل البعد عن المساحة التي كنت أخذ العينات أو عليك توليد المصفوفات فريدة.
سنستخدم \(\nu = 3\) لذلك لدينا ضعيفة قبل، وسوف نتخذ \(V = \frac{1}{\nu} I\) التي ستسحب تقدير التغاير لدينا نحو الهوية (أذكر أن المتوسط هو \(\nu V\)).
PRIOR_DF = 3
PRIOR_SCALE = np.eye(2, dtype=np.float32) / PRIOR_DF
def log_lik_prior_numpy(precision):
rv = scipy.stats.wishart(df=PRIOR_DF, scale=PRIOR_SCALE)
return rv.logpdf(precision)
# test case: compute the prior for the true parameters
log_lik_prior_numpy(true_precision)
-9.103606346649766
توزيع ويشارت هو قبل المترافقة لتقدير مصفوفة دقة طبيعية المتغيرات ذات المعروف يعني \(\mu\).
لنفترض أن المعلمات يشارت السابقة هي \(\nu, V\) وأن لدينا \(n\) ملاحظات لدينا متعدد المتغيرات وضعها الطبيعي، \(x_1, \ldots, x_n\). المعلمات الخلفية هي \(n + \nu, \left(V^{-1} + \sum_{i=1}^n (x_i-\mu)(x_i-\mu)^T \right)^{-1}\).
n = my_data.shape[0]
nu_prior = PRIOR_DF
v_prior = PRIOR_SCALE
nu_posterior = nu_prior + n
v_posterior = np.linalg.inv(np.linalg.inv(v_prior) + my_data.T.dot(my_data))
posterior_mean = nu_posterior * v_posterior
v_post_diag = np.expand_dims(np.diag(v_posterior), axis=1)
posterior_sd = np.sqrt(nu_posterior *
(v_posterior ** 2.0 + v_post_diag.dot(v_post_diag.T)))
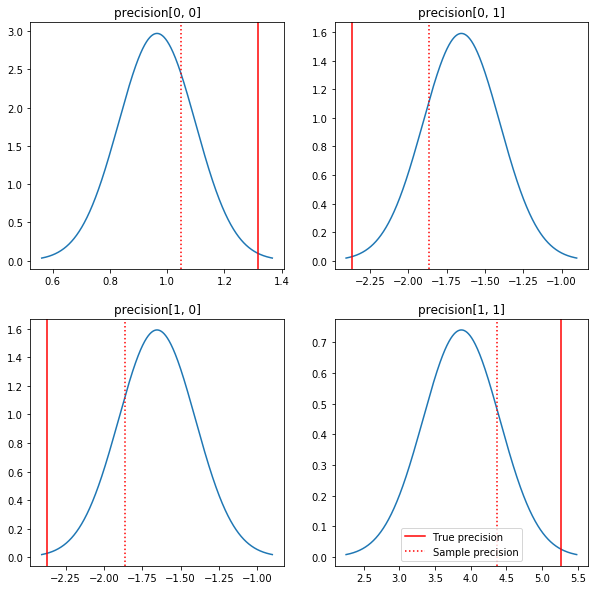
حبكة سريعة للخلفيات والقيم الحقيقية. لاحظ أن الأجزاء الخلفية قريبة من النماذج الخلفية ولكنها تتقلص قليلاً نحو الهوية. لاحظ أيضًا أن القيم الحقيقية بعيدة جدًا عن الوضع اللاحق - ويفترض أن هذا يرجع إلى أن البيانات السابقة ليست مطابقة جيدة جدًا لبياناتنا. في مشكلة حقيقية لكنا على الأرجح القيام بعمل أفضل مع شيء من هذا القبيل تحجيم معكوس يشارت قبل لالتغاير (انظر، على سبيل المثال، أندرو غيلمان في التعليق على هذا الموضوع)، ولكن بعد ذلك نحن لن يكون لها الخلفي التحليلية لطيفة.
sample_precision = np.linalg.inv(np.cov(my_data, rowvar=False, bias=False))
fig, axes = plt.subplots(2, 2)
fig.set_size_inches(10, 10)
for i in range(2):
for j in range(2):
ax = axes[i, j]
loc = posterior_mean[i, j]
scale = posterior_sd[i, j]
xmin = loc - 3.0 * scale
xmax = loc + 3.0 * scale
x = np.linspace(xmin, xmax, 1000)
y = scipy.stats.norm.pdf(x, loc=loc, scale=scale)
ax.plot(x, y)
ax.axvline(true_precision[i, j], color='red', label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':', label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.legend()
plt.show()
الخطوة 3: تنفيذ وظيفة الاحتمال في TensorFlow
المفسد: محاولتنا الأولى لن تنجح ؛ سنتحدث عن السبب أدناه.
نصيحة: استخدام TensorFlow وضع حريصة عند وضع دالة الإمكان الخاص بك. وضع حريصة يجعل TF تتصرف أشبه نمباي - كل شيء ينفذ على الفور، حتى تتمكن من تصحيح تفاعلي بدلا من الاضطرار إلى استخدام Session.run() . راجع الملاحظات هنا .
تمهيدية: فئات التوزيع
يحتوي TFP على مجموعة من فئات التوزيع التي سنستخدمها لإنشاء احتمالات السجل لدينا. شيء واحد يجب ملاحظته هو أن هذه الفئات تعمل مع موترات من العينات بدلاً من عينات مفردة فقط - وهذا يسمح بالتوجيه والتعجيلات ذات الصلة.
يمكن أن يعمل التوزيع مع موتر من العينات بطريقتين مختلفتين. من الأسهل توضيح هاتين الطريقتين بمثال ملموس يتضمن توزيعًا باستخدام معلمة عددية واحدة. أنا استخدم بواسون التوزيع، والتي لديها rate المعلمة.
- إذا كان لنا أن إنشاء بواسون مع قيمة واحدة ل
rateالمعلمة، دعوة إلى للsample()طريقة بإرجاع قيمة واحدة. وتسمى هذه القيمة علىevent، وفي هذه الحالة الأحداث كلها سكالارس. - إذا كان لنا أن إنشاء بواسون مع موتر من قيم
rateالمعلمة، دعوة إلى للsample()الأسلوب بإرجاع الآن قيم متعددة، واحد لكل قيمة في موتر معدل. يعمل الكائن كمجموعة من Poissons مستقلة، ولكل منها سعره الخاص، ولكل من القيم التي يتم إرجاعها بواسطة استدعاءsample()يتوافق مع واحدة من هذه Poissons. وهذا ما يسمى مجموعة من الفعاليات المستقلة ولكن لم توزع مماثل فيbatch. - في
sample()يأخذ الأسلوبsample_shapeالمعلمة التي التخلف إلى الصفوف (tuple) فارغة. تمرير قيمة غير فارغة لsample_shapeالنتائج في عينة عودة دفعات متعددة. وتسمى هذه المجموعة من دفعات علىsample.
والتوزيع في log_prob() طريقة يستهلك البيانات بطريقة التشابه كيف sample() يولد ذلك. log_prob() يعود الاحتمالات للعينات، أي لمتعددة، دفعات مستقلة للأحداث.
- اذا كان لدينا جسم الحوت لدينا التي تم إنشاؤها مع عددي
rate، كل دفعة هي العددية، وإذا كنا تمر في الموترة للعينات، وسوف يخرج من موتر من نفس الحجم من احتمالات السجل. - اذا كان لدينا جسم الحوت لدينا التي تم إنشاؤها مع موتر من شكل
Tمنrateالقيم، كل دفعة هي موتر من شكلT. إذا مررنا موترًا لعينات من الشكل D ، T ، فسنخرج موترًا لاحتمالات اللوغاريتمات للشكل D ، T.
فيما يلي بعض الأمثلة التي توضح هذه الحالات. نرى هذا الكمبيوتر الدفتري لتعليمي أكثر تفصيلا عن الأحداث، دفعات، والأشكال.
# case 1: get log probabilities for a vector of iid draws from a single
# normal distribution
norm1 = tfd.Normal(loc=0., scale=1.)
probs1 = norm1.log_prob(tf.constant([1., 0.5, 0.]))
# case 2: get log probabilities for a vector of independent draws from
# multiple normal distributions with different parameters. Note the vector
# values for loc and scale in the Normal constructor.
norm2 = tfd.Normal(loc=[0., 2., 4.], scale=[1., 1., 1.])
probs2 = norm2.log_prob(tf.constant([1., 0.5, 0.]))
print('iid draws from a single normal:', probs1.numpy())
print('draws from a batch of normals:', probs2.numpy())
iid draws from a single normal: [-1.4189385 -1.0439385 -0.9189385] draws from a batch of normals: [-1.4189385 -2.0439386 -8.918939 ]
احتمالية تسجيل البيانات
سنقوم أولاً بتنفيذ وظيفة احتمالية سجل البيانات.
VALIDATE_ARGS = True
ALLOW_NAN_STATS = False
يتمثل أحد الاختلافات الرئيسية عن حالة NumPy في أن دالة احتمالية TensorFlow الخاصة بنا ستحتاج إلى التعامل مع متجهات المصفوفات الدقيقة بدلاً من مجرد مصفوفات فردية. سيتم استخدام نواقل المعلمات عندما نقوم بأخذ عينات من سلاسل متعددة.
سننشئ كائن توزيع يعمل مع مجموعة من المصفوفات الدقيقة (أي مصفوفة واحدة لكل سلسلة).
عند حساب احتمالات سجل بياناتنا ، سنحتاج إلى نسخ بياناتنا بنفس طريقة متغيراتنا بحيث يكون هناك نسخة واحدة لكل متغير دفعة. يجب أن يكون شكل البيانات المنسوخة كما يلي:
[sample shape, batch shape, event shape]
في حالتنا ، شكل الحدث هو 2 (لأننا نعمل مع 2-D Gaussians). شكل العينة 100 ، لأن لدينا 100 عينة. سيكون شكل الدُفعة هو عدد المصفوفات الدقيقة التي نعمل معها. يعد تكرار البيانات في كل مرة نطلق عليها وظيفة الاحتمالية إهدارًا ، لذلك سنقوم بتكرار البيانات مقدمًا ونمرر النسخة المنسوخة.
لاحظ أن هذا هو تنفيذ فعال: MultivariateNormalFullCovariance مكلفة بالنسبة لبعض البدائل التي سنتحدث عنها في القسم الأمثل في نهاية المطاف.
def log_lik_data(precisions, replicated_data):
n = tf.shape(precisions)[0] # number of precision matrices
# We're estimating a precision matrix; we have to invert to get log
# probabilities. Cholesky inversion should be relatively efficient,
# but as we'll see later, it's even better if we can avoid doing the Cholesky
# decomposition altogether.
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# For our test, we'll use a tensor of 2 precision matrices.
# We'll need to replicate our data for the likelihood function.
# Remember, TFP wants the data to be structured so that the sample dimensions
# are first (100 here), then the batch dimensions (2 here because we have 2
# precision matrices), then the event dimensions (2 because we have 2-D
# Gaussian data). We'll need to add a middle dimension for the batch using
# expand_dims, and then we'll need to create 2 replicates in this new dimension
# using tile.
n = 2
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
print(replicated_data.shape)
(100, 2, 2)
نصيحة: شيء واحد لقد وجدت لتكون مفيدة للغاية وكتابة الشيكات التعقل قليلا من الوظائف TensorFlow بلدي. من السهل حقًا إفساد الموجه في TF ، لذا فإن وجود وظائف NumPy الأبسط يعد طريقة رائعة للتحقق من إخراج TF. فكر في هذه على أنها اختبارات وحدة صغيرة.
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_data(precisions, replicated_data=replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
احتمالية تسجيل سابقة
السابق أسهل لأنه لا داعي للقلق بشأن نسخ البيانات.
@tf.function(autograph=False)
def log_lik_prior(precisions):
rv_precision = tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions)
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_prior(precisions).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]))
print('tensorflow:', lik_tf[i])
0 numpy: -2.2351873809649625 tensorflow: -2.2351875 1 numpy: -9.103606346649766 tensorflow: -9.103608
بناء وظيفة احتمالية السجل المشترك
تعتمد وظيفة احتمالية سجل البيانات أعلاه على ملاحظاتنا ، لكن لن يمتلكها جهاز أخذ العينات. يمكننا التخلص من التبعية دون استخدام متغير عام باستخدام [إغلاق] (https://en.wikipedia.org/wiki/Closure_ (computer_programming). تتضمن عمليات الإغلاق وظيفة خارجية تنشئ بيئة تحتوي على متغيرات يحتاجها الوظيفة الداخلية.
def get_log_lik(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik(precision):
return log_lik_data(precision, replicated_data) + log_lik_prior(precision)
return _log_lik
الخطوة 4: نموذج
حسنًا ، حان وقت أخذ العينات! لتبسيط الأمور ، سنستخدم سلسلة واحدة فقط وسنستخدم مصفوفة الوحدة كنقطة بداية. سنفعل الأشياء بعناية أكبر لاحقًا.
مرة أخرى ، لن ينجح هذا - سنحصل على استثناء.
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.expand_dims(tf.eye(2), axis=0)
# Use expand_dims because we want to pass in a tensor of starting values
log_lik_fn = get_log_lik(my_data, n_chains=1)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
return states
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
Cholesky decomposition was not successful. The input might not be valid.
[[{ {node mcmc_sample_chain/trace_scan/while/body/_79/smart_for_loop/while/body/_371/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_537/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/StatefulPartitionedCall/Cholesky} }]] [Op:__inference_sample_2849]
Function call stack:
sample
...
Function call stack:
sample
تحديد المشكلة
InvalidArgumentError (see above for traceback): Cholesky decomposition was not successful. The input might not be valid. هذا ليس مفيدًا للغاية. دعونا نرى ما إذا كان بإمكاننا معرفة المزيد عما حدث.
- سنطبع المعلمات لكل خطوة حتى نتمكن من رؤية القيمة التي تفشل فيها الأشياء
- سنضيف بعض التأكيدات للحماية من مشاكل معينة.
التأكيدات صعبة لأنها عمليات TensorFlow ، وعلينا أن نحرص على تنفيذها ولا يتم تحسينها من الرسم البياني. انها تستحق القراءة هذه اللمحة من TensorFlow التصحيح إذا كنت لم تكن مألوفة مع تأكيدات TF. يمكنك فرض صراحة التأكيدات لتنفيذ باستخدام tf.control_dependencies (انظر التعليقات في التعليمات البرمجية أدناه).
الأم TensorFlow في Print وظيفة لها نفس السلوك كما التأكيدات - انها عملية، وتحتاج إلى اتخاذ بعض الحذر لضمان أن ينفذ. Print تسبب الصداع إضافية عندما كنا نعمل في دفتر: يتم إرسال انتاجها الى stderr ، و stderr لا يتم عرضها في الخلية. سنستخدم خدعة هنا: بدلا من استخدام tf.Print ، سنقوم خلق منطقتنا عملية TensorFlow الطباعة عبر tf.pyfunc . كما هو الحال مع التأكيدات ، علينا التأكد من تنفيذ طريقتنا.
def get_log_lik_verbose(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
def _log_lik(precisions):
# An internal method we'll make into a TensorFlow operation via tf.py_func
def _print_precisions(precisions):
print('precisions:\n', precisions)
return False # operations must return something!
# Turn our method into a TensorFlow operation
print_op = tf.compat.v1.py_func(_print_precisions, [precisions], tf.bool)
# Assertions are also operations, and some care needs to be taken to ensure
# that they're executed
assert_op = tf.assert_equal(
precisions, tf.linalg.matrix_transpose(precisions),
message='not symmetrical', summarize=4, name='symmetry_check')
# The control_dependencies statement forces its arguments to be executed
# before subsequent operations
with tf.control_dependencies([print_op, assert_op]):
return (log_lik_data(precisions, replicated_data) +
log_lik_prior(precisions))
return _log_lik
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.eye(2)[tf.newaxis, ...]
log_lik_fn = get_log_lik_verbose(my_data)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[ 0.24315196 -0.2761638 ]
[-0.33882257 0.8622 ]]]
assertion failed: [not symmetrical] [Condition x == y did not hold element-wise:] [x (leapfrog_integrate_one_step/add:0) = ] [[[0.243151963 -0.276163787][-0.338822573 0.8622]]] [y (leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/matrix_transpose/transpose:0) = ] [[[0.243151963 -0.338822573][-0.276163787 0.8622]]]
[[{ {node mcmc_sample_chain/trace_scan/while/body/_96/smart_for_loop/while/body/_381/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_503/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/symmetry_check_1/Assert/AssertGuard/else/_577/Assert} }]] [Op:__inference_sample_4837]
Function call stack:
sample
...
Function call stack:
sample
لماذا فشل هذا
أول قيمة معلمة جديدة يحاولها أخذ العينات هي مصفوفة غير متماثلة. يؤدي هذا إلى فشل تحلل Cholesky ، حيث يتم تعريفه فقط للمصفوفات المتماثلة (والمحددة الإيجابية).
تكمن المشكلة هنا في أن المعلمة التي تهمنا هي مصفوفة دقيقة ، ويجب أن تكون مصفوفات الدقة حقيقية ومتماثلة وإيجابية محددة. لا يعرف جهاز أخذ العينات أي شيء عن هذا القيد (باستثناء ربما من خلال التدرجات) ، لذلك من الممكن تمامًا أن يقترح جهاز أخذ العينات قيمة غير صالحة ، مما يؤدي إلى استثناء ، خاصة إذا كان حجم الخطوة كبيرًا.
باستخدام أداة أخذ العينات Hamiltonian Monte Carlo ، قد نتمكن من حل المشكلة باستخدام حجم خطوة صغير جدًا ، حيث يجب أن يحافظ التدرج اللوني على المعلمات بعيدًا عن المناطق غير الصالحة ، ولكن أحجام الخطوات الصغيرة تعني تقاربًا بطيئًا. مع جهاز أخذ العينات Metropolis-Hastings ، الذي لا يعرف شيئًا عن التدرجات ، فإننا محكوم علينا بالفشل.
الإصدار 2: إعادة ضبط المعاملات إلى معايير غير مقيدة
يوجد حل مباشر للمشكلة أعلاه: يمكننا إعادة معاملات نموذجنا بحيث لا تحتوي المعلمات الجديدة على هذه القيود. يوفر TFP مجموعة مفيدة من الأدوات - عوامل التحيز - للقيام بذلك بالضبط.
إعادة المعامله مع bijectors
يجب أن تكون مصفوفة الدقة لدينا حقيقية ومتماثلة ؛ نريد معلمات بديلة لا تحتوي على هذه القيود. نقطة البداية هي تحليل عوامل تشوليسكي لمصفوفة الدقة. لا تزال عوامل Cholesky مقيدة - فهي مثلثة منخفضة ، ويجب أن تكون عناصرها القطرية موجبة. ومع ذلك ، إذا أخذنا سجل الأقطار لعامل Cholesky ، فلن تكون السجلات مقيدة لتكون موجبة ، ثم إذا قمنا بتسوية الجزء المثلثي السفلي إلى متجه 1-D ، فلن يكون لدينا قيد المثلث السفلي . ستكون النتيجة في حالتنا متجهًا بطول 3 بدون قيود.
(و دليل ستان له فصلا كبيرا على استخدام التحولات لإزالة أنواع مختلفة من القيود على المعلمات.)
هذا الإصلاح له تأثير ضئيل على وظيفة احتمالية سجل البيانات لدينا - علينا فقط قلب تحولنا حتى نستعيد مصفوفة الدقة - لكن التأثير على السابق أكثر تعقيدًا. لقد حددنا أن احتمال مصفوفة دقة معينة يتم الحصول عليه من توزيع Wishart ؛ ما هو احتمال المصفوفة المحولة؟
تذكر أنه إذا كنا تطبيق دالة رتيبة \(g\) إلى 1-D متغير عشوائي \(X\)، \(Y = g(X)\)، وكثافة ل \(Y\) تعطى من قبل
\[ f_Y(y) = | \frac{d}{dy}(g^{-1}(y)) | f_X(g^{-1}(y)) \]
مشتق من \(g^{-1}\) المدى حسابات للطريقة التي \(g\) تغيير وحدات التخزين المحلية. للمتغيرات العشوائية أعلى من الأبعاد، فإن العامل التصحيحي هو القيمة المطلقة المحدد من مصفوفه جاكوبي من \(g^{-1}\) (انظر هنا ).
سيتعين علينا إضافة Jacobian من معكوس التحويل إلى دالة الاحتمال المسبق للسجل لدينا. لحسن الحظ، TFP في Bijector يمكن أن الطبقة رعاية هذا بالنسبة لنا.
و Bijector يستخدم فئة لتمثيل للانعكاس، وظائف ناعمة تستخدم لتغيير المتغيرات في دالة الكثافة الاحتمالية. Bijectors يكون كل شيء forward() الطريقة التي ينفذ تحويل، وهو inverse() الطريقة التي المقلوب ذلك، و forward_log_det_jacobian() و inverse_log_det_jacobian() الطرق التي توفر التصحيحات مصفوفه جاكوبي نحتاج عندما كنا reparaterize قوات الدفاع الشعبي.
يوفر TFP مجموعة من bijectors المفيد أن نتمكن من الجمع من خلال تكوين عبر Chain مشغل لتشكيل التحويلات معقدة للغاية. في حالتنا ، سنقوم بتكوين عوامل التحيز الثلاثة التالية (يتم تنفيذ العمليات في السلسلة من اليمين إلى اليسار):
- تتمثل الخطوة الأولى في تحويلنا في إجراء تحليل عوامل تشوليسكي على مصفوفة الدقة. لا توجد فئة Bijector لذلك ؛ ومع ذلك، فإن
CholeskyOuterProductbijector يأخذ المنتج من 2 العوامل Cholesky. يمكننا استخدام عكس هذه العملية باستخدامInvertالمشغل. - الخطوة التالية هي أخذ سجل العناصر القطرية لعامل تشوليسكي. علينا أن ننجز هذا عن طريق
TransformDiagonalbijector ومعكوسExpbijector. - وأخيرا نحن لشد الجزء السفلي من الثلاثي مصفوفة لناقلات باستخدام معكوس
FillTriangularbijector.
# Our transform has 3 stages that we chain together via composition:
precision_to_unconstrained = tfb.Chain([
# step 3: flatten the lower triangular portion of the matrix
tfb.Invert(tfb.FillTriangular(validate_args=VALIDATE_ARGS)),
# step 2: take the log of the diagonals
tfb.TransformDiagonal(tfb.Invert(tfb.Exp(validate_args=VALIDATE_ARGS))),
# step 1: decompose the precision matrix into its Cholesky factors
tfb.Invert(tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS)),
])
# sanity checks
m = tf.constant([[1., 2.], [2., 8.]])
m_fwd = precision_to_unconstrained.forward(m)
m_inv = precision_to_unconstrained.inverse(m_fwd)
# bijectors handle tensors of values, too!
m2 = tf.stack([m, tf.eye(2)])
m2_fwd = precision_to_unconstrained.forward(m2)
m2_inv = precision_to_unconstrained.inverse(m2_fwd)
print('single input:')
print('m:\n', m.numpy())
print('precision_to_unconstrained(m):\n', m_fwd.numpy())
print('inverse(precision_to_unconstrained(m)):\n', m_inv.numpy())
print()
print('tensor of inputs:')
print('m2:\n', m2.numpy())
print('precision_to_unconstrained(m2):\n', m2_fwd.numpy())
print('inverse(precision_to_unconstrained(m2)):\n', m2_inv.numpy())
single input: m: [[1. 2.] [2. 8.]] precision_to_unconstrained(m): [0.6931472 2. 0. ] inverse(precision_to_unconstrained(m)): [[1. 2.] [2. 8.]] tensor of inputs: m2: [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]] precision_to_unconstrained(m2): [[0.6931472 2. 0. ] [0. 0. 0. ]] inverse(precision_to_unconstrained(m2)): [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]]
و TransformedDistribution الطبقة بأتمتة عملية تطبيق bijector إلى توزيع وجعل تصحيح مصفوفه جاكوبي الضروري log_prob() . يصبح سابقنا الجديد:
def log_lik_prior_transformed(transformed_precisions):
rv_precision = tfd.TransformedDistribution(
tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS),
bijector=precision_to_unconstrained,
validate_args=VALIDATE_ARGS)
return rv_precision.log_prob(transformed_precisions)
# Check against the numpy implementation. Note that when comparing, we need
# to add in the Jacobian correction.
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_prior_transformed(transformed_precisions).numpy()
corrections = precision_to_unconstrained.inverse_log_det_jacobian(
transformed_precisions, event_ndims=1).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow: -0.84889317 1 numpy: -7.305657151741624 tensorflow: -7.305659
نحتاج فقط إلى عكس التحويل لاحتمالية سجل البيانات لدينا:
precision = precision_to_unconstrained.inverse(transformed_precision)
نظرًا لأننا نريد في الواقع تحليل عوامل Cholesky لمصفوفة الدقة ، فسيكون من الأفضل عمل معكوس جزئي هنا. ومع ذلك ، سنترك التحسين لاحقًا وسنترك معكوسًا جزئيًا كتمرين للقارئ.
def log_lik_data_transformed(transformed_precisions, replicated_data):
# We recover the precision matrix by inverting our bijector. This is
# inefficient since we really want the Cholesky decomposition of the
# precision matrix, and the bijector has that in hand during the inversion,
# but we'll worry about efficiency later.
n = tf.shape(transformed_precisions)[0]
precisions = precision_to_unconstrained.inverse(transformed_precisions)
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# sanity check
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_data_transformed(
transformed_precisions, replicated_data).numpy()
for i in range(precisions.shape[0]):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
مرة أخرى نختتم وظائفنا الجديدة في الخاتمة.
def get_log_lik_transformed(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_transformed(transformed_precisions):
return (log_lik_data_transformed(transformed_precisions, replicated_data) +
log_lik_prior_transformed(transformed_precisions))
return _log_lik_transformed
# make sure everything runs
log_lik_fn = get_log_lik_transformed(my_data)
m = tf.eye(2)[tf.newaxis, ...]
lik = log_lik_fn(precision_to_unconstrained.forward(m)).numpy()
print(lik)
[-431.5611]
أخذ العينات
الآن بما أنه لا داعي للقلق بشأن تفجير جهاز أخذ العينات لدينا بسبب قيم المعلمات غير الصالحة ، فلنقم بإنشاء بعض العينات الحقيقية.
يعمل جهاز أخذ العينات مع الإصدار غير المقيّد لمعلماتنا ، لذلك نحتاج إلى تحويل قيمتنا الأولية إلى نسختها غير المقيدة. ستكون جميع العينات التي ننتجها أيضًا في شكلها غير المقيد ، لذلك نحتاج إلى إعادة تحويلها مرة أخرى. يتم توجيه الأجسام البينية ، لذلك من السهل القيام بذلك.
# We'll choose a proper random initial value this time
np.random.seed(123)
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_value = initial_value_cholesky.dot(
initial_value_cholesky.T)[np.newaxis, ...]
# The sampler works with unconstrained values, so we'll transform our initial
# value
initial_value_transformed = precision_to_unconstrained.forward(
initial_value).numpy()
# Sample!
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data, n_chains=1)
num_results = 1000
num_burnin_steps = 1000
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
initial_value_transformed,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=lambda _, pkr: pkr.is_accepted,
seed=123)
# transform samples back to their constrained form
precision_samples = [precision_to_unconstrained.inverse(s) for s in states]
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
دعنا نقارن متوسط ناتج جهاز أخذ العينات الخاص بنا بالمتوسط التحليلي اللاحق!
print('True posterior mean:\n', posterior_mean)
print('Sample mean:\n', np.mean(np.reshape(precision_samples, [-1, 2, 2]), axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Sample mean: [[ 1.4315274 -0.25587553] [-0.25587553 0.5740424 ]]
نحن بعيدون جدا! دعونا نفهم السبب. دعونا أولاً نلقي نظرة على عيناتنا.
np.reshape(precision_samples, [-1, 2, 2])
array([[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
...,
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]]], dtype=float32)
عذرًا - يبدو أن لديهم جميعًا نفس القيمة. دعونا نفهم السبب.
و kernel_results_ المتغير هو الصفوف (tuple) المسمى الذي يعطي معلومات عن أخذ العينات في كل دولة. و is_accepted الحقل هو المفتاح هنا.
# Look at the acceptance for the last 100 samples
print(np.squeeze(is_accepted)[-100:])
print('Fraction of samples accepted:', np.mean(np.squeeze(is_accepted)))
[False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False] Fraction of samples accepted: 0.0
تم رفض جميع عيناتنا! من المفترض أن حجم خطوتنا كان كبيرًا جدًا. اخترت stepsize=0.1 تعسفية بحتة.
الإصدار 3: أخذ العينات بحجم خطوة تكيفية
منذ فشل أخذ العينات من خياري التعسفي لحجم الخطوة ، لدينا بعض بنود جدول الأعمال:
- تنفيذ حجم خطوة تكيفية ، و
- إجراء بعض فحوصات التقارب.
هناك بعض التعليمات البرمجية لطيفة في tensorflow_probability/python/mcmc/hmc.py لتنفيذ أحجام خطوة على التكيف. لقد قمت بتكييفه أدناه.
ملاحظة هذا هناك منفصلة sess.run() بيان لكل خطوة. هذا مفيد حقًا لتصحيح الأخطاء ، لأنه يتيح لنا إضافة بعض التشخيصات لكل خطوة بسهولة إذا لزم الأمر. على سبيل المثال ، يمكننا إظهار التقدم التدريجي ، ووقت كل خطوة ، وما إلى ذلك.
نصيحة: طريقة واحدة على ما يبدو مشتركة لخبط أخذ العينات الخاصة بك هو أن يكون تنمو الرسم البياني الخاص بك في الحلقة. (السبب في إنهاء الرسم البياني قبل تشغيل الجلسة هو منع مثل هذه المشكلات فقط.) إذا لم تكن تستخدم finalize () ، على الرغم من ذلك ، فإن التحقق المفيد من تصحيح الأخطاء إذا كان الرمز الخاص بك يتباطأ إلى الزحف هو طباعة الرسم البياني حجم في كل خطوة عن طريق len(mygraph.get_operations()) - إن الزيادات طول، وربما كنت تفعل شيئا سيئا.
سنقوم بتشغيل 3 سلاسل مستقلة هنا. سيساعدنا إجراء بعض المقارنات بين السلاسل في التحقق من التقارب.
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values = []
for i in range(N_CHAINS):
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_values.append(initial_value_cholesky.dot(initial_value_cholesky.T))
initial_values = np.stack(initial_values)
initial_values_transformed = precision_to_unconstrained.forward(
initial_values).numpy()
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=hmc,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values_transformed,
kernel=adapted_kernel,
trace_fn=lambda _, pkr: pkr.inner_results.is_accepted,
parallel_iterations=1)
# transform samples back to their constrained form
precision_samples = precision_to_unconstrained.inverse(states)
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
فحص سريع: معدل قبولنا أثناء أخذ العينات لدينا قريب من هدفنا البالغ 0.651.
print(np.mean(is_accepted))
0.6190666666666667
والأفضل من ذلك ، أن متوسط العينة والانحراف المعياري قريبان مما نتوقعه من الحل التحليلي.
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96426415 -1.6519215 ] [-1.6519215 3.8614824 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13622096 0.25235635] [0.25235635 0.5394968 ]]
التحقق من التقارب
بشكل عام ، لن يكون لدينا حل تحليلي لمراجعته ، لذلك سنحتاج إلى التأكد من تقارب جهاز أخذ العينات. واحد الاختيار هو معيار لغيلمان روبين \(\hat{R}\) الإحصائية، الأمر الذي يتطلب سلاسل أخذ العينات متعددة. \(\hat{R}\) التدابير الدرجة التي التباين (وسائل) بين سلاسل يتجاوز ما يتوقعه المرء إذا تم توزيع السلاسل مماثل. قيم \(\hat{R}\) تستخدم ما يقرب من 1 تشير إلى تقارب تقريبي. انظر المصدر لمزيد من التفاصيل.
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0038308 1.0005717] [1.0005717 1.0006068]]
نموذج النقد
إذا لم يكن لدينا حل تحليلي ، فسيكون هذا هو الوقت المناسب للقيام ببعض النقد النموذجي الحقيقي.
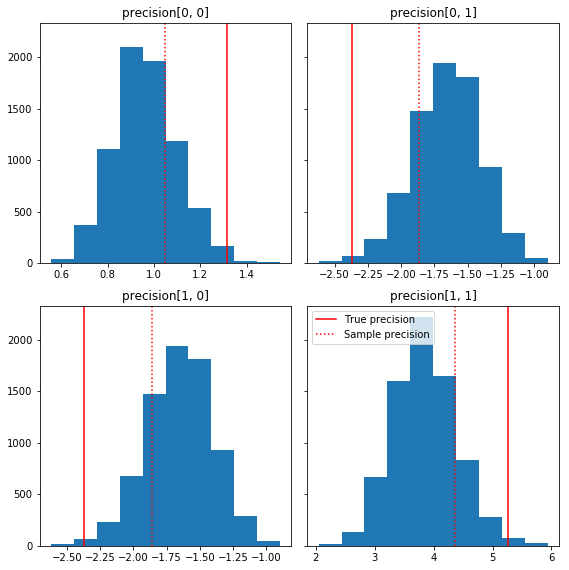
فيما يلي بعض الرسوم البيانية السريعة لمكونات العينة بالنسبة إلى الحقيقة الأساسية لدينا (باللون الأحمر). لاحظ أنه تم تقليص العينات من قيم مصفوفة دقة العينة باتجاه مصفوفة الهوية مسبقًا.
fig, axes = plt.subplots(2, 2, sharey=True)
fig.set_size_inches(8, 8)
for i in range(2):
for j in range(2):
ax = axes[i, j]
ax.hist(precision_samples_reshaped[:, i, j])
ax.axvline(true_precision[i, j], color='red',
label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':',
label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.tight_layout()
plt.legend()
plt.show()
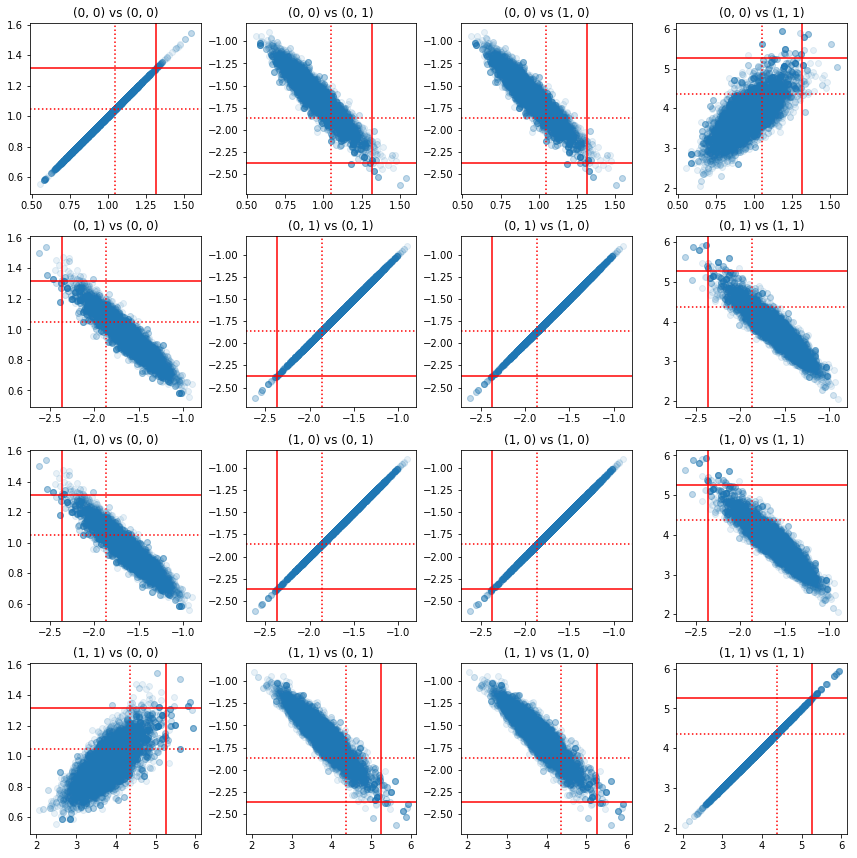
تُظهر بعض المخططات المبعثرة لأزواج المكونات الدقيقة أنه بسبب بنية الارتباط للجزء الخلفي ، فإن القيم الخلفية الحقيقية ليست مستبعدة كما تظهر من الهامش أعلاه.
fig, axes = plt.subplots(4, 4)
fig.set_size_inches(12, 12)
for i1 in range(2):
for j1 in range(2):
index1 = 2 * i1 + j1
for i2 in range(2):
for j2 in range(2):
index2 = 2 * i2 + j2
ax = axes[index1, index2]
ax.scatter(precision_samples_reshaped[:, i1, j1],
precision_samples_reshaped[:, i2, j2], alpha=0.1)
ax.axvline(true_precision[i1, j1], color='red')
ax.axhline(true_precision[i2, j2], color='red')
ax.axvline(sample_precision[i1, j1], color='red', linestyle=':')
ax.axhline(sample_precision[i2, j2], color='red', linestyle=':')
ax.set_title('(%d, %d) vs (%d, %d)' % (i1, j1, i2, j2))
plt.tight_layout()
plt.show()
الإصدار 4: أخذ عينات أبسط للمعلمات المقيدة
جعلت Bijectors أخذ العينات من مصفوفة الدقة مباشرة ، ولكن كان هناك قدر لا بأس به من التحويل اليدوي من التمثيل غير المقيد وإليه. هناك طريقة أسهل!
نواة TransformedTransformed
و TransformedTransitionKernel تسهيل هذه العملية. إنه يلف جهاز أخذ العينات ويتعامل مع جميع التحويلات. تأخذ قائمة من bijectors التي تعين قيم المعلمات غير المقيدة للقيم المقيدة كوسيطة. حتى هنا نحن بحاجة إلى معكوس precision_to_unconstrained bijector كنا أعلاه. نحن يمكن فقط استخدام tfb.Invert(precision_to_unconstrained) ، ولكن هذا ينطوي على أخذ العكوس من العكوس (TensorFlow لا يكفي الذكية لتبسيط tf.Invert(tf.Invert()) ل tf.Identity()) ، وذلك بدلا نحن سأقوم فقط بكتابة bijector جديد.
تقييد البازع
# The bijector we need for the TransformedTransitionKernel is the inverse of
# the one we used above
unconstrained_to_precision = tfb.Chain([
# step 3: take the product of Cholesky factors
tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS),
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: map a vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# quick sanity check
m = [[1., 2.], [2., 8.]]
m_inv = unconstrained_to_precision.inverse(m).numpy()
m_fwd = unconstrained_to_precision.forward(m_inv).numpy()
print('m:\n', m)
print('unconstrained_to_precision.inverse(m):\n', m_inv)
print('forward(unconstrained_to_precision.inverse(m)):\n', m_fwd)
m: [[1.0, 2.0], [2.0, 8.0]] unconstrained_to_precision.inverse(m): [0.6931472 2. 0. ] forward(unconstrained_to_precision.inverse(m)): [[1. 2.] [2. 8.]]
أخذ العينات باستخدام TransformedTransitionKernel
مع TransformedTransitionKernel ، لم يعد لدينا للقيام التحولات اليدوية لمعاييرنا. قيمنا الأولية وعيناتنا كلها مصفوفات دقيقة ؛ علينا فقط أن نمرر في المحرض (المحرضين) غير المقيدين إلى النواة وهو يعتني بجميع التحولات.
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
return states
precision_samples = sample()
التحقق من التقارب
و \(\hat{R}\) يبدو الاختيار التقارب جيدة!
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013582 1.0019467] [1.0019467 1.0011805]]
مقارنة مع التحليلي اللاحق
مرة أخرى دعونا نتحقق من الجزء الخلفي التحليلي.
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96687526 -1.6552585 ] [-1.6552585 3.867676 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329624 0.24913791] [0.24913791 0.53983927]]
التحسينات
الآن بعد أن أصبح لدينا أشياء تعمل من البداية إلى النهاية ، فلنقم بإصدار أكثر تحسينًا. لا تهم السرعة كثيرًا في هذا المثال ، ولكن بمجرد زيادة حجم المصفوفات ، ستحدث بعض التحسينات فرقًا كبيرًا.
أحد التحسينات الكبيرة التي يمكننا إجراؤها على السرعة هو إعادة المعاملات من حيث تحلل تشوليسكي. السبب هو أن وظيفة احتمالية البيانات الخاصة بنا تتطلب كلاً من التباين المشترك ومصفوفات الدقة. مصفوفة انعكاس غير مكلفة (\(O(n^3)\) ل \(n \times n\) المصفوفة)، وإذا كنا بالحدود من حيث إما التغاير أو مصفوفة الدقة، وتحتاج علينا القيام به انعكاس للحصول على الآخر.
وللتذكير، حقيقية، سواء كان إيجابيا-محددة، متماثل مصفوفة \(M\) يمكن أن تتحلل إلى منتج النموذج \(M = L L^T\) حيث مصفوفة \(L\) هو أقل الثلاثي ولها أقطار إيجابية. ونظرا لتحلل Cholesky من \(M\)، يمكننا الحصول على أكثر كفاءة على حد سواء \(M\) (نتاج الدنيا ومصفوفة الثلاثي العليا) و \(M^{-1}\) (عبر العودة الاستبدال). إن تحليل عوامل Cholesky بحد ذاته ليس رخيصًا للحساب ، ولكن إذا حددنا بارامترات من حيث عوامل Cholesky ، فإننا نحتاج فقط إلى حساب عامل Choleksy لقيم المعلمات الأولية.
استخدام تحلل Cholesky لمصفوفة التغاير
TFP لديه نسخة من التوزيع الطبيعي المتعدد، MultivariateNormalTriL ، وهذا هو معلمات من حيث عامل Cholesky من مصفوفة التغاير. لذلك إذا أردنا تحديد المعلمات من حيث عامل Cholesky لمصفوفة التغاير ، فيمكننا حساب احتمالية سجل البيانات بكفاءة. يكمن التحدي في حساب احتمالية السجل السابق بكفاءة مماثلة.
إذا كان لدينا نسخة من توزيع Wishart المعكوس الذي يعمل مع عوامل Cholesky للعينات ، فسنكون جميعًا جاهزين. للأسف ، نحن لا نفعل ذلك. (سيرحب الفريق بعمليات إرسال الشفرات ، على الرغم من ذلك!) كبديل ، يمكننا استخدام نسخة من توزيع Wishart الذي يعمل مع عوامل Cholesky من العينات جنبًا إلى جنب مع سلسلة من bijectors.
في الوقت الحالي ، نحن نفتقد عددًا قليلاً من أدوات تحيز الأسهم لجعل الأشياء فعالة حقًا ، لكني أريد أن أظهر العملية كتدريب وتوضيح مفيد لقوة أدوات تحيز TFP.
توزيع Wishart يعمل على عوامل Cholesky
و Wishart التوزيع لديه العلم المفيد، input_output_cholesky ، التي تنص على أن المدخلات والمخرجات المصفوفات يجب أن تكون العوامل Cholesky. يعتبر العمل مع عوامل تشوليسكي أكثر كفاءة وأكثر فائدة من الناحية العددية من استخدام المصفوفات الكاملة ، وهذا هو السبب في أن هذا أمر مرغوب فيه. نقطة هامة حول دلالات العلم: انها مجرد إشارة إلى أن تمثيل المدخلات والمخرجات لتوزيع يجب أن تتغير - لا تشير إلى وجود reparameterization الكاملة للتوزيع، التي من شأنها أن تنطوي على تصحيح مصفوفه جاكوبي إلى log_prob() وظيفة. نريد في الواقع إجراء هذا الإصلاح الكامل ، لذلك سنبني التوزيع الخاص بنا.
# An optimized Wishart distribution that has been transformed to operate on
# Cholesky factors instead of full matrices. Note that we gain a modest
# additional speedup by specifying the Cholesky factor of the scale matrix
# (i.e. by passing in the scale_tril parameter instead of scale).
class CholeskyWishart(tfd.TransformedDistribution):
"""Wishart distribution reparameterized to use Cholesky factors."""
def __init__(self,
df,
scale_tril,
validate_args=False,
allow_nan_stats=True,
name='CholeskyWishart'):
# Wishart has a bunch of methods that we want to support but not
# implement. We'll subclass TransformedDistribution here to take care of
# those. We'll override the few for which speed is critical and implement
# them with a separate Wishart for which input_output_cholesky=True
super(CholeskyWishart, self).__init__(
distribution=tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=False,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()),
validate_args=validate_args,
name=name
)
# Here's the Cholesky distribution we'll use for log_prob() and sample()
self.cholesky = tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=True,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats)
def _log_prob(self, x):
return (self.cholesky.log_prob(x) +
self.bijector.inverse_log_det_jacobian(x, event_ndims=2))
def _sample_n(self, n, seed=None):
return self.cholesky._sample_n(n, seed)
# some checks
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
@tf.function(autograph=False)
def compute_log_prob(m):
w_transformed = tfd.TransformedDistribution(
tfd.WishartTriL(df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()))
w_optimized = CholeskyWishart(
df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY)
log_prob_transformed = w_transformed.log_prob(m)
log_prob_optimized = w_optimized.log_prob(m)
return log_prob_transformed, log_prob_optimized
for matrix in [np.eye(2, dtype=np.float32),
np.array([[1., 0.], [2., 8.]], dtype=np.float32)]:
log_prob_transformed, log_prob_optimized = [
t.numpy() for t in compute_log_prob(matrix)]
print('Transformed Wishart:', log_prob_transformed)
print('Optimized Wishart', log_prob_optimized)
Transformed Wishart: -0.84889317 Optimized Wishart -0.84889317 Transformed Wishart: -99.269455 Optimized Wishart -99.269455
بناء توزيع Wishart معكوس
لدينا مصفوفة التغاير \(C\) متحللة في \(C = L L^T\) حيث \(L\) هو أقل الثلاثي وله قطري إيجابي. نريد أن نعرف من احتمال \(L\) بالنظر إلى أن \(C \sim W^{-1}(\nu, V)\) حيث \(W^{-1}\) هو معكوس توزيع يشارت.
توزيع ويشارت معكوس لديه خاصية أنه إذا \(C \sim W^{-1}(\nu, V)\)، ثم دقة مصفوفة \(C^{-1} \sim W(\nu, V^{-1})\). حتى نتمكن من الحصول على احتمال \(L\) عبر TransformedDistribution أن يأخذ كمعلمات توزيع يشارت وbijector التي تعين عامل Cholesky مصفوفة الدقة إلى عامل Cholesky من عكسه.
وهناك طريقة واضحة (ولكن ليس كفاءة فائقة) للحصول من عامل Cholesky من \(C^{-1}\) إلى \(L\) هو عكس عامل Cholesky التي ظهر حل، ثم تشكيل مصفوفة التغاير من هذه العوامل مقلوب، ثم القيام إلى عوامل Cholesky .
السماح للتحلل Cholesky من \(C^{-1} = M M^T\). \(M\) هو أقل الثلاثي، حتى نتمكن من عكس ذلك باستخدام MatrixInverseTriL bijector.
تشكيل \(C\) من \(M^{-1}\) هي صعبة قليلا: \(C = (M M^T)^{-1} = M^{-T}M^{-1} = M^{-T} (M^{-T})^T\). \(M\) هو أقل الثلاثي، لذلك \(M^{-1}\) سيكون أيضا أقل الثلاثي، و \(M^{-T}\) سيكون الثلاثي العلوي. و CholeskyOuterProduct() bijector يعمل فقط مع المصفوفات الثلاثي أقل، لذلك نحن لا يمكن استخدامها لتكوين \(C\) من \(M^{-T}\). الحل البديل الخاص بنا هو سلسلة من العناصر الحيوية التي تعمل على تبديل صفوف وأعمدة المصفوفة.
لحسن الحظ يتم تغليف هذا المنطق في CholeskyToInvCholesky bijector!
الجمع بين كل القطع
# verify that the bijector works
m = np.array([[1., 0.], [2., 8.]], dtype=np.float32)
c_inv = m.dot(m.T)
c = np.linalg.inv(c_inv)
c_chol = np.linalg.cholesky(c)
wishart_cholesky_to_iw_cholesky = tfb.CholeskyToInvCholesky()
w_fwd = wishart_cholesky_to_iw_cholesky.forward(m).numpy()
print('numpy =\n', c_chol)
print('bijector =\n', w_fwd)
numpy = [[ 1.0307764 0. ] [-0.03031695 0.12126781]] bijector = [[ 1.0307764 0. ] [-0.03031695 0.12126781]]
توزيعنا النهائي
يعمل Wishart المعكوس على عوامل Cholesky على النحو التالي:
inverse_wishart_cholesky = tfd.TransformedDistribution(
distribution=CholeskyWishart(
df=PRIOR_DF,
scale_tril=np.linalg.cholesky(np.linalg.inv(PRIOR_SCALE))),
bijector=tfb.CholeskyToInvCholesky())
لدينا معكوس Wishart ، لكنه بطيء نوعًا ما لأنه يتعين علينا إجراء تحلل Cholesky في bijector. دعنا نعود إلى معلمات مصفوفة الدقة ونرى ما يمكننا القيام به هناك من أجل التحسين.
الإصدار النهائي (!): استخدام تحلل Cholesky لمصفوفة الدقة
نهج بديل هو العمل مع عوامل Cholesky لمصفوفة الدقة. هنا يسهل حساب وظيفة الاحتمال المسبق ، لكن وظيفة احتمالية تسجيل البيانات تتطلب مزيدًا من العمل نظرًا لأن TFP لا يحتوي على إصدار من المتغيرات العادية المتعددة المتغيرات التي تم تحديد معلماتها بدقة.
محسن احتمالية تسجيل سابقة
نحن نستخدم CholeskyWishart توزيع بنينا فوق لبناء قبل.
# Our new prior.
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
def log_lik_prior_cholesky(precisions_cholesky):
rv_precision = CholeskyWishart(
df=PRIOR_DF,
scale_tril=PRIOR_SCALE_CHOLESKY,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions_cholesky)
# Check against the slower TF implementation and the NumPy implementation.
# Note that when comparing to NumPy, we need to add in the Jacobian correction.
precisions = [np.eye(2, dtype=np.float32),
true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
lik_tf = log_lik_prior_cholesky(precisions_cholesky).numpy()
lik_tf_slow = tfd.TransformedDistribution(
distribution=tfd.WishartTriL(
df=PRIOR_DF, scale_tril=tf.linalg.cholesky(PRIOR_SCALE)),
bijector=tfb.Invert(tfb.CholeskyOuterProduct())).log_prob(
precisions_cholesky).numpy()
corrections = tfb.Invert(tfb.CholeskyOuterProduct()).inverse_log_det_jacobian(
precisions_cholesky, event_ndims=2).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow slow:', lik_tf_slow[i])
print('tensorflow fast:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow slow: -0.84889317 tensorflow fast: -0.84889317 1 numpy: -7.442875031036973 tensorflow slow: -7.442877 tensorflow fast: -7.442876
احتمالية سجل البيانات الأمثل
We can use TFP's bijectors to build our own version of the multivariate normal. Here is the key idea:
Suppose I have a column vector \(X\) whose elements are iid samples of \(N(0, 1)\). We have \(\text{mean}(X) = 0\) and \(\text{cov}(X) = I\)
Now let \(Y = A X + b\). We have \(\text{mean}(Y) = b\) and \(\text{cov}(Y) = A A^T\)
Hence we can make vectors with mean \(b\) and covariance \(C\) using the affine transform \(Ax+b\) to vectors of iid standard Normal samples provided \(A A^T = C\). The Cholesky decomposition of \(C\) has the desired property. However, there are other solutions.
Let \(P = C^{-1}\) and let the Cholesky decomposition of \(P\) be \(B\), ie \(B B^T = P\). Now
\(P^{-1} = (B B^T)^{-1} = B^{-T} B^{-1} = B^{-T} (B^{-T})^T\)
So another way to get our desired mean and covariance is to use the affine transform \(Y=B^{-T}X + b\).
Our approach (courtesy of this notebook ):
- Use
tfd.Independent()to combine a batch of 1-DNormalrandom variables into a single multi-dimensional random variable. Thereinterpreted_batch_ndimsparameter forIndependent()specifies the number of batch dimensions that should be reinterpreted as event dimensions. In our case we create a 1-D batch of length 2 that we transform into a 1-D event of length 2, soreinterpreted_batch_ndims=1. - Apply a bijector to add the desired covariance:
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky, adjoint=True)). Note that above we're multiplying our iid normal random variables by the transpose of the inverse of the Cholesky factor of the precision matrix \((B^{-T}X)\). Thetfb.Inverttakes care of inverting \(B\), and theadjoint=Trueflag performs the transpose. - Apply a bijector to add the desired offset:
tfb.Shift(shift=shift)Note that we have to do the shift as a separate step from the initial inverted affine transform because otherwise the inverted scale is applied to the shift (since the inverse of \(y=Ax+b\) is \(x=A^{-1}y - A^{-1}b\)).
class MVNPrecisionCholesky(tfd.TransformedDistribution):
"""Multivariate normal parameterized by loc and Cholesky precision matrix."""
def __init__(self, loc, precision_cholesky, name=None):
super(MVNPrecisionCholesky, self).__init__(
distribution=tfd.Independent(
tfd.Normal(loc=tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky,
adjoint=True)),
]),
name=name)
@tf.function(autograph=False)
def log_lik_data_cholesky(precisions_cholesky, replicated_data):
n = tf.shape(precisions_cholesky)[0] # number of precision matrices
rv_data = MVNPrecisionCholesky(
loc=tf.zeros([n, 2]),
precision_cholesky=precisions_cholesky)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# check against the numpy implementation
true_precision_cholesky = np.linalg.cholesky(true_precision)
precisions = [np.eye(2, dtype=np.float32), true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
n = precisions_cholesky.shape[0]
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
lik_tf = log_lik_data_cholesky(precisions_cholesky, replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.81824
Combined log likelihood function
Now we combine our prior and data log likelihood functions in a closure.
def get_log_lik_cholesky(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_cholesky(precisions_cholesky):
return (log_lik_data_cholesky(precisions_cholesky, replicated_data) +
log_lik_prior_cholesky(precisions_cholesky))
return _log_lik_cholesky
Constraining bijector
Our samples are constrained to be valid Cholesky factors, which means they must be lower triangular matrices with positive diagonals. The TransformedTransitionKernel needs a bijector that maps unconstrained tensors to/from tensors with our desired constraints. We've removed the Cholesky decomposition from the bijector's inverse, which speeds things up.
unconstrained_to_precision_cholesky = tfb.Chain([
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: expand the vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# some checks
inv = unconstrained_to_precision_cholesky.inverse(precisions_cholesky).numpy()
fwd = unconstrained_to_precision_cholesky.forward(inv).numpy()
print('precisions_cholesky:\n', precisions_cholesky)
print('\ninv:\n', inv)
print('\nfwd(inv):\n', fwd)
precisions_cholesky: [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]] inv: [[ 0.0000000e+00 0.0000000e+00 0.0000000e+00] [ 3.5762781e-07 -2.0647411e+00 1.3721828e-01]] fwd(inv): [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]]
Initial values
We generate a tensor of initial values. We're working with Cholesky factors, so we generate some Cholesky factor initial values.
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values_cholesky = []
for i in range(N_CHAINS):
initial_values_cholesky.append(np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32))
initial_values_cholesky = np.stack(initial_values_cholesky)
Sampling
We sample N_CHAINS chains using the TransformedTransitionKernel .
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_cholesky(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision_cholesky)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
samples = tf.linalg.matmul(states, states, transpose_b=True)
return samples
precision_samples = sample()
Convergence check
A quick convergence check looks good:
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013583 1.0019467] [1.0019467 1.0011804]]
Comparing results to the analytic posterior
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, newshape=[-1, 2, 2])
And again, the sample means and standard deviations match those of the analytic posterior.
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.9668749 -1.6552604] [-1.6552604 3.8676758]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329637 0.24913797] [0.24913797 0.53983945]]
Ok, all done! We've got our optimized sampler working.
