 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Dans ce cahier, nous allons explorer les distributions TensorFlow (TFD en abrégé). L'objectif de ce cahier est de vous faire progresser en douceur dans la courbe d'apprentissage, y compris la compréhension du traitement par TFD des formes tensorielles. Ce cahier essaie de présenter des exemples avant plutôt que des concepts abstraits. Nous présenterons d'abord des moyens simples et canoniques de faire les choses et enregistrerons la vue abstraite la plus générale jusqu'à la fin. Si vous êtes le type qui préfère un tutoriel plus abstrait et le style de référence, consultez Comprendre tensorflow Distributions formes . Si vous avez des questions sur le matériel ici, ne hésitez pas à contacter (ou joindre) la liste de diffusion de probabilité tensorflow . Nous sommes heureux de vous aider.
Avant de commencer, nous devons importer les bibliothèques appropriées. Notre bibliothèque globale est tensorflow_probability . Par convention, on se réfère généralement à la bibliothèque de distributions tfd .
Tensorflow Avide est un environnement d'exécution impératif pour tensorflow. Dans TensorFlow Avid, chaque opération TF est immédiatement évaluée et produit un résultat. Cela contraste avec le mode "graphique" standard de TensorFlow, dans lequel les opérations TF ajoutent des nœuds à un graphique qui est ensuite exécuté. Tout ce bloc-notes est écrit à l'aide de TF Eager, bien qu'aucun des concepts présentés ici ne repose sur cela, et TFP peut être utilisé en mode graphique.
import collections
import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions
try:
tf.compat.v1.enable_eager_execution()
except ValueError:
pass
import matplotlib.pyplot as plt
Distributions univariées de base
Plongeons-nous et créons une distribution normale :
n = tfd.Normal(loc=0., scale=1.)
n
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
On peut en tirer un échantillon :
n.sample()
<tf.Tensor: shape=(), dtype=float32, numpy=0.25322816>
Nous pouvons prélever plusieurs échantillons :
n.sample(3)
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.4658079, -0.5653636, 0.9314412], dtype=float32)>
On peut évaluer un log prob :
n.log_prob(0.)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>
Nous pouvons évaluer plusieurs probabilités de log :
n.log_prob([0., 2., 4.])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-0.9189385, -2.9189386, -8.918939 ], dtype=float32)>
Nous avons une large gamme de distributions. Essayons un Bernoulli :
b = tfd.Bernoulli(probs=0.7)
b
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[] event_shape=[] dtype=int32>
b.sample()
<tf.Tensor: shape=(), dtype=int32, numpy=1>
b.sample(8)
<tf.Tensor: shape=(8,), dtype=int32, numpy=array([1, 0, 0, 0, 1, 0, 1, 0], dtype=int32)>
b.log_prob(1)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.35667497>
b.log_prob([1, 0, 1, 0])
<tf.Tensor: shape=(4,), dtype=float32, numpy=array([-0.35667497, -1.2039728 , -0.35667497, -1.2039728 ], dtype=float32)>
Distributions multivariées
Nous allons créer une normale multivariée avec une covariance diagonale :
nd = tfd.MultivariateNormalDiag(loc=[0., 10.], scale_diag=[1., 4.])
nd
<tfp.distributions.MultivariateNormalDiag 'MultivariateNormalDiag' batch_shape=[] event_shape=[2] dtype=float32>
En comparant cela à la normale univariée que nous avons créée plus tôt, qu'est-ce qui est différent ?
tfd.Normal(loc=0., scale=1.)
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
Nous voyons que la normale univariée a un event_shape de () , ce qui indique qu'il est une distribution scalaire. L'une normale multivariée a event_shape de 2 , ce qui indique la [espace de réunion] de base (https://en.wikipedia.org/wiki/Event_ (probability_theory)) de cette distribution est à deux dimensions.
L'échantillonnage fonctionne comme avant :
nd.sample()
<tf.Tensor: shape=(2,), dtype=float32, numpy=array([-1.2489667, 15.025171 ], dtype=float32)>
nd.sample(5)
<tf.Tensor: shape=(5, 2), dtype=float32, numpy=
array([[-1.5439653 , 8.9968405 ],
[-0.38730723, 12.448896 ],
[-0.8697963 , 9.330035 ],
[-1.2541095 , 10.268944 ],
[ 2.3475595 , 13.184147 ]], dtype=float32)>
nd.log_prob([0., 10])
<tf.Tensor: shape=(), dtype=float32, numpy=-3.2241714>
Les normales multivariées n'ont généralement pas de covariance diagonale. TFD offre plusieurs façons de créer des normales multivariées, y compris une spécification de covariance complète, que nous utilisons ici.
nd = tfd.MultivariateNormalFullCovariance(
loc = [0., 5], covariance_matrix = [[1., .7], [.7, 1.]])
data = nd.sample(200)
plt.scatter(data[:, 0], data[:, 1], color='blue', alpha=0.4)
plt.axis([-5, 5, 0, 10])
plt.title("Data set")
plt.show()
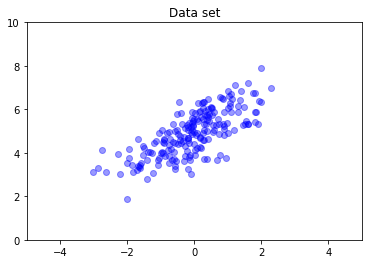
Distributions multiples
Notre première distribution de Bernoulli représentait un lancer d'une seule pièce équitable. Nous pouvons également créer un lot de distributions de Bernoulli indépendants, chacun avec leurs propres paramètres, en une seule Distribution objet:
b3 = tfd.Bernoulli(probs=[.3, .5, .7])
b3
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[3] event_shape=[] dtype=int32>
Il est important d'être clair sur ce que cela signifie. L'appel ci - dessus définit trois distributions de Bernoulli indépendantes, qui se trouvent être contenues dans le même python Distribution objet. Les trois distributions ne peuvent pas être manipulées individuellement. Notez comment le batch_shape est (3,) , ce qui indique un lot de trois distributions, et la event_shape est () , ce qui indique les distributions individuelles ont un espace d'événement univariée.
Si nous appelons sample , nous obtenons un échantillon de trois:
b3.sample()
<tf.Tensor: shape=(3,), dtype=int32, numpy=array([0, 1, 1], dtype=int32)>
b3.sample(6)
<tf.Tensor: shape=(6, 3), dtype=int32, numpy=
array([[1, 0, 1],
[0, 1, 1],
[0, 0, 1],
[0, 0, 1],
[0, 0, 1],
[0, 1, 0]], dtype=int32)>
Si nous appelons prob , (ce qui a la même sémantique de forme que log_prob , nous utilisons prob avec ces petits exemples Bernoulli pour plus de clarté, bien que log_prob est généralement préférée dans les applications) , nous pouvons transmettre un vecteur et d' évaluer la probabilité de chaque pièce cédant cette valeur :
b3.prob([1, 1, 0])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.29999998, 0.5 , 0.29999998], dtype=float32)>
Pourquoi l'API inclut-elle une forme de lot ? Sémantiquement, on peut effectuer les mêmes calculs en créant une liste des distributions et itérer sur eux avec une for boucle (au moins en mode Eager, en mode graphique TF vous auriez besoin d' une tf.while boucle). Cependant, avoir un ensemble (potentiellement grand) de distributions paramétrées de manière identique est extrêmement courant, et l'utilisation de calculs vectorisés chaque fois que possible est un ingrédient clé pour pouvoir effectuer des calculs rapides à l'aide d'accélérateurs matériels.
Utilisation d'Independent pour agréger des lots en événements
Dans la section précédente, nous avons créé b3 , une seule Distribution objet qui a représenté trois pièces flips. Si nous avons appelé b3.prob sur un vecteur \(v\), le \(i\)« e entrée était la probabilité que le \(i\)ème pièce prend la valeur \(v[i]\).
Supposons que nous souhaitions plutôt spécifier une distribution "jointe" sur des variables aléatoires indépendantes de la même famille sous-jacente. Ceci est un autre objet mathématiquement, en ce que pour cette nouvelle distribution, prob sur un vecteur \(v\) renvoie une valeur unique représentant la probabilité que l'ensemble des pièces de monnaie correspond au vecteur \(v\).
Comment accomplissons-nous cela? Nous utilisons une distribution « ordre supérieur » appelé Independent , qui prend une distribution et donne une nouvelle distribution avec la forme de lot déplacé à la forme de l' événement:
b3_joint = tfd.Independent(b3, reinterpreted_batch_ndims=1)
b3_joint
<tfp.distributions.Independent 'IndependentBernoulli' batch_shape=[] event_shape=[3] dtype=int32>
Comparez la forme à celle de l'original b3 :
b3
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[3] event_shape=[] dtype=int32>
Comme promis, nous voyons que cette Independent a déplacé la forme de lots dans la forme de l' événement: b3_joint est une distribution unique ( batch_shape = () ) sur un espace d'événements en trois dimensions ( event_shape = (3,) ).
Vérifions la sémantique :
b3_joint.prob([1, 1, 0])
<tf.Tensor: shape=(), dtype=float32, numpy=0.044999998>
Une autre façon d'obtenir le même résultat serait de probabilités de calcul en utilisant b3 et faire la réduction manuellement en multipliant (ou, dans le cas le plus fréquent où les probabilités de log sont utilisées, la somme):
tf.reduce_prod(b3.prob([1, 1, 0]))
<tf.Tensor: shape=(), dtype=float32, numpy=0.044999994>
Indpendent permet à l'utilisateur de représenter plus explicitement le concept souhaité. Nous considérons cela comme extrêmement utile, bien que ce ne soit pas strictement nécessaire.
Faits amusants:
-
b3.sampleetb3_joint.sampleont différentes implémentations conceptuelles, mais les résultats impossibles à distinguer: la différence entre un lot de distributions indépendantes et une distribution unique créée à partir du lot à l' aideIndependentapparaît lors du calcul probabilites, et non lors de l' échantillonnage. -
MultivariateNormalDiagpourrait être mis en œuvre à l' aide des trivialement scalairesNormaletIndependentdes distributions (il est pas réellement mis en œuvre de cette façon, mais il pourrait être).
Lots de distributions multivariées
Créons un lot de trois normales multivariées bidimensionnelles à covariance complète :
nd_batch = tfd.MultivariateNormalFullCovariance(
loc = [[0., 0.], [1., 1.], [2., 2.]],
covariance_matrix = [[[1., .1], [.1, 1.]],
[[1., .3], [.3, 1.]],
[[1., .5], [.5, 1.]]])
nd_batch
<tfp.distributions.MultivariateNormalFullCovariance 'MultivariateNormalFullCovariance' batch_shape=[3] event_shape=[2] dtype=float32>
Nous voyons batch_shape = (3,) , donc il y a trois Normales à plusieurs variables indépendantes et event_shape = (2,) , de sorte que chaque normale multivariée est à deux dimensions. Dans cet exemple, les distributions individuelles n'ont pas d'éléments indépendants.
Travaux d'échantillonnage :
nd_batch.sample(4)
<tf.Tensor: shape=(4, 3, 2), dtype=float32, numpy=
array([[[ 0.7367498 , 2.730996 ],
[-0.74080074, -0.36466932],
[ 0.6516018 , 0.9391426 ]],
[[ 1.038303 , 0.12231752],
[-0.94788766, -1.204232 ],
[ 4.059758 , 3.035752 ]],
[[ 0.56903946, -0.06875849],
[-0.35127294, 0.5311631 ],
[ 3.4635801 , 4.565582 ]],
[[-0.15989424, -0.25715637],
[ 0.87479895, 0.97391707],
[ 0.5211419 , 2.32108 ]]], dtype=float32)>
Depuis batch_shape = (3,) et event_shape = (2,) , on passe un tenseur de forme (3, 2) à log_prob :
nd_batch.log_prob([[0., 0.], [1., 1.], [2., 2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.8328519, -1.7907217, -1.694036 ], dtype=float32)>
La radiodiffusion, alias Pourquoi est-ce si déroutant ?
Abstraire ce que nous avons fait jusqu'à présent, toutes les distributions a une forme lot B et une forme d'événement E . Laissez - BE la concaténation des formes d'événements:
- Pour les distributions scalaires univariées
netb,BE = ().. - Pour les Normales à plusieurs variables en deux dimensions
nd.BE = (2). - Pour les deux
b3etb3_joint,BE = (3). - Pour le lot de plusieurs variables normales
ndb,BE = (3, 2).
Les « règles d'évaluation » que nous avons utilisées jusqu'à présent sont :
- Échantillon sans argument renvoie un tenseur de forme
BE; échantillonnage avec un scalaire n renvoie un « n parBEtenseur ». -
probetlog_probprendre un tenseur de formeBEet retourner un résultat de la formeB.
La « règle d'évaluation » réelle pour prob et log_prob est plus compliquée, d'une manière qui offre une puissance potentielle et la vitesse , mais aussi la complexité et les défis. La règle actuelle est (essentiellement) que l'argument de log_prob doit être diffusable contre BE ; toutes les dimensions "supplémentaires" sont conservées dans la sortie.
Explorons les implications. Pour la normale univariée n , BE = () , donc log_prob attend un scalaire. Si on passe log_prob un tenseur de forme non vide, les dimensions apparaissent comme des lots dans la sortie:
n = tfd.Normal(loc=0., scale=1.)
n
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
n.log_prob(0.)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>
n.log_prob([0.])
<tf.Tensor: shape=(1,), dtype=float32, numpy=array([-0.9189385], dtype=float32)>
n.log_prob([[0., 1.], [-1., 2.]])
<tf.Tensor: shape=(2, 2), dtype=float32, numpy=
array([[-0.9189385, -1.4189385],
[-1.4189385, -2.9189386]], dtype=float32)>
Tour Let aux deux dimensions normale à plusieurs variables nd (paramètres modifiés pour des fins d' illustration):
nd = tfd.MultivariateNormalDiag(loc=[0., 1.], scale_diag=[1., 1.])
nd
<tfp.distributions.MultivariateNormalDiag 'MultivariateNormalDiag' batch_shape=[] event_shape=[2] dtype=float32>
log_prob « prévoit » un argument de forme (2,) , mais il acceptera tout argument selon lequel les émissions contre cette forme:
nd.log_prob([0., 0.])
<tf.Tensor: shape=(), dtype=float32, numpy=-2.337877>
Mais nous pouvons passer « plus » des exemples, et d' évaluer tous leurs log_prob est à la fois:
nd.log_prob([[0., 0.],
[1., 1.],
[2., 2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-2.337877 , -2.337877 , -4.3378773], dtype=float32)>
Peut-être moins attrayant, nous pouvons diffuser sur les dimensions de l'événement :
nd.log_prob([0.])
<tf.Tensor: shape=(), dtype=float32, numpy=-2.337877>
nd.log_prob([[0.], [1.], [2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-2.337877 , -2.337877 , -4.3378773], dtype=float32)>
La diffusion de cette manière est une conséquence de notre conception « permettre la diffusion chaque fois que possible » ; cette utilisation est quelque peu controversée et pourrait potentiellement être supprimée dans une future version de TFP.
Regardons maintenant à nouveau l'exemple des trois pièces :
b3 = tfd.Bernoulli(probs=[.3, .5, .7])
Ici, en utilisant la diffusion pour représenter la probabilité que chaque pièce arrive tête est assez intuitive:
b3.prob([1])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.29999998, 0.5 , 0.7 ], dtype=float32)>
(Comparez cela à b3.prob([1., 1., 1.]) , que nous aurions de nouveau utilisé où b3 a été introduit.)
Supposons maintenant que nous voulons savoir, pour chaque pièce, la probabilité de la pièce arrive la tête et la probabilité qu'il arrive queue. On pourrait imaginer essayer :
b3.log_prob([0, 1])
Malheureusement, cela produit une erreur avec une trace de pile longue et peu lisible. b3 a BE = (3) , nous devons donc passer b3.prob diffusable quelque chose contre (3,) . [0, 1] a une forme (2) , de sorte qu'il ne diffuse pas et crée une erreur. Au lieu de cela, nous devons dire:
b3.prob([[0], [1]])
<tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[0.7, 0.5, 0.3],
[0.3, 0.5, 0.7]], dtype=float32)>
Pourquoi? [[0], [1]] a une forme (2, 1) , de sorte qu'il diffuse contre la forme (3) pour faire une forme de diffusion de (2, 3) .
La diffusion est assez puissante : il y a des cas où elle permet une réduction par ordre de grandeur de la quantité de mémoire utilisée, et elle raccourcit souvent le code utilisateur. Cependant, il peut être difficile de programmer avec. Si vous appelez log_prob et obtenez une erreur, un manque de diffusion est presque toujours le problème.
Aller plus loin
Dans ce tutoriel, nous avons (espérons-le) fourni une introduction simple. Quelques pistes pour aller plus loin :
-
event_shape,batch_shapeetsample_shapepeuvent être rang arbitraire (dans ce tutoriel , ils sont toujours soit scalaire ou de rang 1). Cela augmente la puissance mais peut encore une fois entraîner des problèmes de programmation, en particulier lorsque la diffusion est impliquée. Pour une plongée profonde supplémentaire dans la manipulation de forme, voir les Comprendre tensorflow Distributions formes . - TFP comprend une abstraction puissante connue sous le nom
Bijectors, qui , en conjonction avecTransformedDistribution, donne une souplesse, de composition pour créer facilement de nouvelles distributions qui sont des transformations inversible des distributions existantes. Nous allons essayer d'écrire un tutoriel sur ce sujet bientôt, mais en attendant, consultez la documentation
