 Посмотреть на TensorFlow.org Посмотреть на TensorFlow.org |  Запускаем в Google Colab Запускаем в Google Colab |  Посмотреть исходный код на GitHub Посмотреть исходный код на GitHub |  Скачать блокнот Скачать блокнот |
В этой записной книжке мы рассмотрим дистрибутивы TensorFlow (сокращенно TFD). Цель этой записной книжки - помочь вам плавно подняться по кривой обучения, включая понимание того, как TFD обрабатывает тензорные формы. В этой записной книжке делается попытка представить примеры, а не абстрактные концепции. Сначала мы представим канонические простые способы решения задач и сохраним наиболее общий абстрактный вид до конца. Если вы тип , который предпочитает более абстрактный и справочно-стиль учебник, проверить Понимание TensorFlow распределений фигур . Если у вас есть какие - либо вопросы по поводу материала здесь, не стесняйтесь обращаться к (или присоединиться) список рассылки Вероятность TensorFlow . Мы рады помочь.
Прежде чем мы начнем, нам нужно импортировать соответствующие библиотеки. Наша общая библиотека tensorflow_probability . По соглашению, мы обычно относятся к библиотеке распределений как tfd .
Tensorflow Нетерпеливый является императивом среда исполнения для TensorFlow. В TensorFlow eager каждая операция TF немедленно оценивается и дает результат. Это контрастирует со стандартным режимом «графа» TensorFlow, в котором операции TF добавляют узлы к графу, который позже выполняется. Вся эта записная книжка написана с использованием TF Eager, хотя ни одна из представленных здесь концепций не основывается на этом, и TFP можно использовать в графическом режиме.
import collections
import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions
try:
tf.compat.v1.enable_eager_execution()
except ValueError:
pass
import matplotlib.pyplot as plt
Базовые одномерные распределения
Давайте углубимся и создадим нормальное распределение:
n = tfd.Normal(loc=0., scale=1.)
n
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
Мы можем извлечь из него образец:
n.sample()
<tf.Tensor: shape=(), dtype=float32, numpy=0.25322816>
Мы можем нарисовать несколько образцов:
n.sample(3)
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.4658079, -0.5653636, 0.9314412], dtype=float32)>
Мы можем оценить ошибку журнала:
n.log_prob(0.)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>
Мы можем оценить несколько вероятностей журнала:
n.log_prob([0., 2., 4.])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-0.9189385, -2.9189386, -8.918939 ], dtype=float32)>
У нас есть широкий выбор дистрибутивов. Давайте попробуем Бернулли:
b = tfd.Bernoulli(probs=0.7)
b
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[] event_shape=[] dtype=int32>
b.sample()
<tf.Tensor: shape=(), dtype=int32, numpy=1>
b.sample(8)
<tf.Tensor: shape=(8,), dtype=int32, numpy=array([1, 0, 0, 0, 1, 0, 1, 0], dtype=int32)>
b.log_prob(1)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.35667497>
b.log_prob([1, 0, 1, 0])
<tf.Tensor: shape=(4,), dtype=float32, numpy=array([-0.35667497, -1.2039728 , -0.35667497, -1.2039728 ], dtype=float32)>
Многовариантные распределения
Мы создадим многомерную нормаль с диагональной ковариацией:
nd = tfd.MultivariateNormalDiag(loc=[0., 10.], scale_diag=[1., 4.])
nd
<tfp.distributions.MultivariateNormalDiag 'MultivariateNormalDiag' batch_shape=[] event_shape=[2] dtype=float32>
Сравнивая это с одномерной нормалью, которую мы создали ранее, чем отличается?
tfd.Normal(loc=0., scale=1.)
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
Мы видим , что одномерный нормальный имеет event_shape из () , что указывает на это скалярная распределение. Многомерное нормальное имеет event_shape из 2 , что указывает на основное пространство для проведения [] (https://en.wikipedia.org/wiki/Event_ (probability_theory)) этого распределения является двумерным.
Сэмплирование работает так же, как и раньше:
nd.sample()
<tf.Tensor: shape=(2,), dtype=float32, numpy=array([-1.2489667, 15.025171 ], dtype=float32)>
nd.sample(5)
<tf.Tensor: shape=(5, 2), dtype=float32, numpy=
array([[-1.5439653 , 8.9968405 ],
[-0.38730723, 12.448896 ],
[-0.8697963 , 9.330035 ],
[-1.2541095 , 10.268944 ],
[ 2.3475595 , 13.184147 ]], dtype=float32)>
nd.log_prob([0., 10])
<tf.Tensor: shape=(), dtype=float32, numpy=-3.2241714>
Многомерные нормали, как правило, не имеют диагональной ковариации. TFD предлагает несколько способов создания многомерных нормалей, включая спецификацию полной ковариации, которую мы здесь используем.
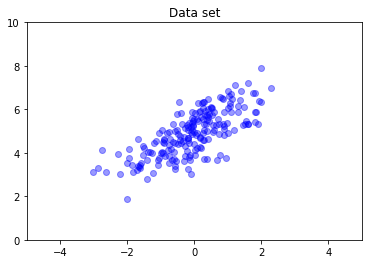
nd = tfd.MultivariateNormalFullCovariance(
loc = [0., 5], covariance_matrix = [[1., .7], [.7, 1.]])
data = nd.sample(200)
plt.scatter(data[:, 0], data[:, 1], color='blue', alpha=0.4)
plt.axis([-5, 5, 0, 10])
plt.title("Data set")
plt.show()
Множественные распределения
Наша первая раздача Бернулли представляла собой подбрасывание единственной справедливой монеты. Мы также можем создать партию независимых Бернулли распределений, каждый со своими собственными параметрами, в одном Distribution объекта:
b3 = tfd.Bernoulli(probs=[.3, .5, .7])
b3
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[3] event_shape=[] dtype=int32>
Важно понимать, что это означает. Выше вызов определяет три независимых распределения Бернулли, которые происходят , которые должны содержаться в одном Python Distribution объекта. Этими тремя дистрибутивами нельзя управлять по отдельности. Обратите внимание , как batch_shape является (3,) , что указывает на партию из трех распределений, а event_shape является () , что указывает на отдельные распределения имеют одномерное пространство для проведения.
Если мы называем sample , мы получаем выборку из всех трех:
b3.sample()
<tf.Tensor: shape=(3,), dtype=int32, numpy=array([0, 1, 1], dtype=int32)>
b3.sample(6)
<tf.Tensor: shape=(6, 3), dtype=int32, numpy=
array([[1, 0, 1],
[0, 1, 1],
[0, 0, 1],
[0, 0, 1],
[0, 0, 1],
[0, 1, 0]], dtype=int32)>
Если мы называем prob , (это имеет ту же форму семантику как log_prob , мы используем prob с этими небольшими примерами Бернулли для ясности, хотя log_prob обычно предпочтительно в приложениях) мы можем передать его вектор и оценить вероятность каждой монеты , дающую это значение :
b3.prob([1, 1, 0])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.29999998, 0.5 , 0.29999998], dtype=float32)>
Почему API включает форму партии? Семантический, один может выполнять то же вычисление, создав список распределений и перебор над ними с for цикла (по крайней мере , в нетерпеливом режиме, в графическом режиме TF вам понадобится tf.while цикл). Однако наличие (потенциально большого) набора идентично параметризованных распределений является чрезвычайно распространенным явлением, и использование векторизованных вычислений, когда это возможно, является ключевым компонентом возможности выполнять быстрые вычисления с использованием аппаратных ускорителей.
Использование независимых пакетов для агрегирования событий
В предыдущем разделе мы создали b3 , один Distribution объект , который представлял три монеты переворачивается. Если мы назвали b3.prob на вектор \(v\), то \(i\)-м запись была вероятность того , что \(i\)- й монеты принимает значение \(v[i]\).
Предположим, мы вместо этого хотели бы указать «совместное» распределение по независимым случайным величинам из одного и того же основного семейства. Это другой объект математически, в том , что для этого нового распределения, prob на вектор \(v\) будет возвращать одно значение , представляющее вероятность того, что весь набор монет соответствует вектору \(v\).
Как мы этого добьемся? Мы используем распределение «высшего порядка» под названием Independent , которая принимает распределение и дает новое распределение с пакетной формы перемещается в форме событий:
b3_joint = tfd.Independent(b3, reinterpreted_batch_ndims=1)
b3_joint
<tfp.distributions.Independent 'IndependentBernoulli' batch_shape=[] event_shape=[3] dtype=int32>
Сравните форму , что оригинальный b3 :
b3
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[3] event_shape=[] dtype=int32>
Как и было обещано, мы видим , что это Independent переместил пакетную форму в форму событий: b3_joint является единственным распределения ( batch_shape = () ) в течение трех-мерном пространстве событий ( event_shape = (3,) ).
Проверим семантику:
b3_joint.prob([1, 1, 0])
<tf.Tensor: shape=(), dtype=float32, numpy=0.044999998>
Альтернативный способ получить тот же результат будет вычислительными вероятностей с использованием b3 и сделать сокращение вручную путем умножения (или, в более обычном случае , когда используются вероятности журнала, суммируя):
tf.reduce_prod(b3.prob([1, 1, 0]))
<tf.Tensor: shape=(), dtype=float32, numpy=0.044999994>
Indpendent позволяет пользователю более четко представлять нужную концепцию. Мы считаем это чрезвычайно полезным, хотя и не совсем необходимым.
Забавные факты:
-
b3.sampleиb3_joint.sampleимеют различные концептуальные реализации, но неразличимых выходы: различие между партией независимых распределений и единым распределением , созданным из партии с использованиемIndependentпоказывает вверх при вычислении probabilites, а не при отборе проб. -
MultivariateNormalDiagможет быть тривиальным реализован с использованием скалярныхNormalиIndependentраспределений (это не на самом деле реализован таким образом, но это может быть).
Партии многомерных распределений
Давайте создадим пакет из трех полноковариационных двумерных многомерных нормалей:
nd_batch = tfd.MultivariateNormalFullCovariance(
loc = [[0., 0.], [1., 1.], [2., 2.]],
covariance_matrix = [[[1., .1], [.1, 1.]],
[[1., .3], [.3, 1.]],
[[1., .5], [.5, 1.]]])
nd_batch
<tfp.distributions.MultivariateNormalFullCovariance 'MultivariateNormalFullCovariance' batch_shape=[3] event_shape=[2] dtype=float32>
Мы видим batch_shape = (3,) , так что есть три независимых многомерные нормалей и event_shape = (2,) , так что каждый многомерное нормальное двумерно. В этом примере отдельные распределения не имеют независимых элементов.
Пробоотборные работы:
nd_batch.sample(4)
<tf.Tensor: shape=(4, 3, 2), dtype=float32, numpy=
array([[[ 0.7367498 , 2.730996 ],
[-0.74080074, -0.36466932],
[ 0.6516018 , 0.9391426 ]],
[[ 1.038303 , 0.12231752],
[-0.94788766, -1.204232 ],
[ 4.059758 , 3.035752 ]],
[[ 0.56903946, -0.06875849],
[-0.35127294, 0.5311631 ],
[ 3.4635801 , 4.565582 ]],
[[-0.15989424, -0.25715637],
[ 0.87479895, 0.97391707],
[ 0.5211419 , 2.32108 ]]], dtype=float32)>
Так как batch_shape = (3,) и event_shape = (2,) , мы переходим тензор формы (3, 2) , чтобы log_prob :
nd_batch.log_prob([[0., 0.], [1., 1.], [2., 2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.8328519, -1.7907217, -1.694036 ], dtype=float32)>
Радиовещание, иначе почему это так сбивает с толку?
Абстрагируясь, что мы делали до сих пор, каждый дистрибутив имеет пакетную форму B и форму события E . Пусть BE конкатенация фигур событий:
- Для одномерных распределений скалярных
nиb,BE = ().. - Для двумерных многомерные нормалей
nd.BE = (2). - Для обоих
b3иb3_joint,BE = (3). - Для партии многомерных нормалей
ndb,BE = (3, 2).
«Правила оценки», которые мы использовали до сих пор:
- Пример без аргумента возвращает тензор с формой
BE; отбор проб с скаляр п возвращает «п наBE» тензорной. -
probиlog_probпринять тензор формыBEи возвращает результат формыB.
Действительное «правила оценки» для prob и log_prob более сложным, таким образом , что обеспечивает потенциальные мощности и скорости , но также сложности и проблемы. Фактическое правило ( по существу) , что аргумент log_prob должен быть broadcastable против BE ; любые «лишние» измерения сохраняются в выводе.
Давайте изучим последствия. Для однофакторного нормального n , BE = () , так что log_prob ожидает скаляр. Если мы передаем log_prob тензора с непустой формой, те появляются как размеры партии в выходе:
n = tfd.Normal(loc=0., scale=1.)
n
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
n.log_prob(0.)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>
n.log_prob([0.])
<tf.Tensor: shape=(1,), dtype=float32, numpy=array([-0.9189385], dtype=float32)>
n.log_prob([[0., 1.], [-1., 2.]])
<tf.Tensor: shape=(2, 2), dtype=float32, numpy=
array([[-0.9189385, -1.4189385],
[-1.4189385, -2.9189386]], dtype=float32)>
Давайте обращусь к двумерный многомерному нормальному nd (параметры изменились в иллюстративных целях):
nd = tfd.MultivariateNormalDiag(loc=[0., 1.], scale_diag=[1., 1.])
nd
<tfp.distributions.MultivariateNormalDiag 'MultivariateNormalDiag' batch_shape=[] event_shape=[2] dtype=float32>
log_prob «ожидает» спор с формой (2,) , но он будет принимать какие - либо аргументы , что вещает против этой формы:
nd.log_prob([0., 0.])
<tf.Tensor: shape=(), dtype=float32, numpy=-2.337877>
Но мы можем перейти в «более» примеров и оценить все их log_prob «S сразу:
nd.log_prob([[0., 0.],
[1., 1.],
[2., 2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-2.337877 , -2.337877 , -4.3378773], dtype=float32)>
Возможно, менее привлекательно, мы можем транслировать по размеру события:
nd.log_prob([0.])
<tf.Tensor: shape=(), dtype=float32, numpy=-2.337877>
nd.log_prob([[0.], [1.], [2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-2.337877 , -2.337877 , -4.3378773], dtype=float32)>
Такое вещание является следствием нашей концепции «разрешать вещание, когда это возможно»; это использование несколько спорно и потенциально может быть удалено в будущей версии TFP.
Теперь давайте снова посмотрим на пример с тремя монетами:
b3 = tfd.Bernoulli(probs=[.3, .5, .7])
Здесь, используя вещание , чтобы представлять вероятность того, что каждая монета упадет орлом вполне интуитивно:
b3.prob([1])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.29999998, 0.5 , 0.7 ], dtype=float32)>
(Сравните это b3.prob([1., 1., 1.]) , которые мы использовали бы обратно , где b3 был введен.)
Теперь предположим , что мы хотим знать, для каждой монеты, то вероятность , что монета упадет орлом , и вероятность , что идет вверх хвосты. Мы могли представить себе попытку:
b3.log_prob([0, 1])
К сожалению, это приводит к ошибке с длинной и не очень удобочитаемой трассировкой стека. b3 имеет BE = (3) , так что мы должны пройти b3.prob что - то broadcastable против (3,) . [0, 1] имеет форму (2) , так что он не передает и создает ошибку. Вместо этого мы должны сказать:
b3.prob([[0], [1]])
<tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[0.7, 0.5, 0.3],
[0.3, 0.5, 0.7]], dtype=float32)>
Почему? [[0], [1]] имеет форму (2, 1) , так что он передает против формы (3) , чтобы сделать широковещательный форму (2, 3) .
Широковещательная передача - это довольно мощный инструмент: в некоторых случаях он позволяет на порядок уменьшить объем используемой памяти и часто делает код пользователя короче. Однако программировать с ним может быть непросто. Если вы звоните log_prob и получить ошибку, отказ вещания почти всегда проблема.
Дальше
В этом руководстве мы (надеюсь) предоставили простое введение. Несколько советов для дальнейшего развития:
-
event_shape,batch_shapeиsample_shapeможет быть произвольным ранга (в данном учебнике они всегда либо скаляр или ранг 1). Это увеличивает мощность, но опять же может привести к проблемам с программированием, особенно когда речь идет о радиовещании. Для дополнительного глубокого погружения в манипуляции формы, см Понимание TensorFlow распределений фигур . - TFP включает в себя мощные абстракции , известные как
Bijectors, который в сочетании сTransformedDistribution, дает гибкий, композиционный способ легко создавать новые распределения , которые являются обратимыми преобразованиями существующих распределений. Мы будем стараться , чтобы написать учебник по этому в ближайшее время , но в то же время, проверить документацию
