Ta strona została przetłumaczona przez Cloud Translation API.

Dystrybucje TensorFlow: delikatne wprowadzenie

Zobacz na TensorFlow.org

Uruchom w Google Colab

Wyświetl źródło na GitHub

Pobierz notatnik

W tym notatniku przyjrzymy się rozkładom TensorFlow (w skrócie TFD). Celem tego notebooka jest delikatne wprowadzenie Cię w krzywą uczenia się, w tym zrozumienie obsługi kształtów tensorów przez TFD. W tym notatniku staramy się przedstawiać przykłady, a nie abstrakcyjne koncepcje. Zaprezentujemy kanoniczne proste sposoby robienia rzeczy najpierw i zachowamy najbardziej ogólny abstrakcyjny widok do końca. Jeśli jesteś typem, który preferuje bardziej abstrakcyjne i odniesienie do stylu samouczek, sprawdź Zrozumienie TensorFlow rozkładów Kształty . Jeśli masz jakieś pytania dotyczące materiału tutaj, nie wahaj się skontaktować (lub dołączyć) listę mailingową Prawdopodobieństwo TensorFlow . Chętnie pomożemy.

Zanim zaczniemy, musimy zaimportować odpowiednie biblioteki. Nasza ogólna biblioteka jest tensorflow_probability . Zgodnie z przyjętą konwencją, na ogół odnoszą się do biblioteki dystrybucji, w sposób tfd .

Tensorflow Marzą to środowisko wykonanie imperatywem TensorFlow. W TensorFlow eager każda operacja TF jest natychmiast oceniana i daje wynik. Jest to przeciwieństwo standardowego trybu „grafu” TensorFlow, w którym operacje TF dodają węzły do grafu, który jest później wykonywany. Cały ten notatnik jest napisany przy użyciu TF Eager, chociaż żadna z przedstawionych tu koncepcji nie opiera się na tym, a TFP może być używany w trybie wykresu.

import collections

import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions

try:
  tf.compat.v1.enable_eager_execution()
except ValueError:
  pass

import matplotlib.pyplot as plt

Podstawowe rozkłady jednowymiarowe

Zanurzmy się od razu i stwórzmy rozkład normalny:

n = tfd.Normal(loc=0., scale=1.)
n

<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>

Możemy z niego pobrać próbkę:

n.sample()

<tf.Tensor: shape=(), dtype=float32, numpy=0.25322816>

Możemy narysować wiele próbek:

n.sample(3)

<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.4658079, -0.5653636,  0.9314412], dtype=float32)>

Możemy ocenić log prob:

n.log_prob(0.)

<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>

Możemy ocenić wiele prawdopodobieństw logarytmu:

n.log_prob([0., 2., 4.])

<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-0.9189385, -2.9189386, -8.918939 ], dtype=float32)>

Posiadamy szeroką gamę dystrybucji. Spróbujmy Bernoulliego:

b = tfd.Bernoulli(probs=0.7)
b

<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[] event_shape=[] dtype=int32>

b.sample()

<tf.Tensor: shape=(), dtype=int32, numpy=1>

b.sample(8)

<tf.Tensor: shape=(8,), dtype=int32, numpy=array([1, 0, 0, 0, 1, 0, 1, 0], dtype=int32)>

b.log_prob(1)

<tf.Tensor: shape=(), dtype=float32, numpy=-0.35667497>

b.log_prob([1, 0, 1, 0])

<tf.Tensor: shape=(4,), dtype=float32, numpy=array([-0.35667497, -1.2039728 , -0.35667497, -1.2039728 ], dtype=float32)>

Dystrybucje wielowymiarowe

Stworzymy wielowymiarową normalną z kowariancją diagonalną:

nd = tfd.MultivariateNormalDiag(loc=[0., 10.], scale_diag=[1., 4.])
nd

<tfp.distributions.MultivariateNormalDiag 'MultivariateNormalDiag' batch_shape=[] event_shape=[2] dtype=float32>

Porównując to z jednowymiarową normalną, którą stworzyliśmy wcześniej, co się zmieniło?

tfd.Normal(loc=0., scale=1.)

<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>

Widzimy, że w jednowymiarowej normalny ma event_shape z () , wskazując, że jest to dystrybucja skalarne. Wielozmienna normalnie ma event_shape z 2 , co wskazuje na podstawową [przestrzeni zdarzeń] (https://en.wikipedia.org/wiki/Event_ (probability_theory)) z tego rozkładu jest dwuwymiarowy.

Samplowanie działa tak samo jak poprzednio:

nd.sample()

<tf.Tensor: shape=(2,), dtype=float32, numpy=array([-1.2489667, 15.025171 ], dtype=float32)>

nd.sample(5)

<tf.Tensor: shape=(5, 2), dtype=float32, numpy=
array([[-1.5439653 ,  8.9968405 ],
       [-0.38730723, 12.448896  ],
       [-0.8697963 ,  9.330035  ],
       [-1.2541095 , 10.268944  ],
       [ 2.3475595 , 13.184147  ]], dtype=float32)>

nd.log_prob([0., 10])

<tf.Tensor: shape=(), dtype=float32, numpy=-3.2241714>

Wielowymiarowe normalne na ogół nie mają kowariancji diagonalnej. TFD oferuje wiele sposobów tworzenia wielowymiarowych normalnych, w tym pełną specyfikację kowariancji, której używamy tutaj.

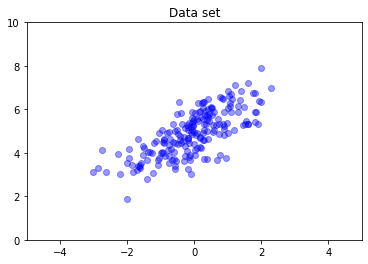
nd = tfd.MultivariateNormalFullCovariance(
    loc = [0., 5], covariance_matrix = [[1., .7], [.7, 1.]])
data = nd.sample(200)
plt.scatter(data[:, 0], data[:, 1], color='blue', alpha=0.4)
plt.axis([-5, 5, 0, 10])
plt.title("Data set")
plt.show()

png

Wiele dystrybucji

Nasza pierwsza dystrybucja Bernoulliego reprezentowała rzut jedną uczciwą monetą. Możemy również utworzyć partię niezależnych rozkład zero-jedynkowy, każdy z własnymi parametrami, w jednym Distribution obiektu:

b3 = tfd.Bernoulli(probs=[.3, .5, .7])
b3

<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[3] event_shape=[] dtype=int32>

Ważne jest, aby jasno określić, co to oznacza. Powyższe wezwanie definiuje trzy niezależne rozkład Bernoulliego, które stało się znajdować w tym samym Pythonie Distribution obiektu. Tych trzech rozkładów nie można manipulować indywidualnie. Uwaga jak batch_shape jest (3,) , co wskazuje na partię trzech rozkładów, a event_shape jest () , wskazując poszczególne dystrybucje mają jednowymiarowego zaplecze konferencyjne.

Jeśli nazywamy sample , dostajemy próbkę ze wszystkich trzech:

b3.sample()

<tf.Tensor: shape=(3,), dtype=int32, numpy=array([0, 1, 1], dtype=int32)>

b3.sample(6)

<tf.Tensor: shape=(6, 3), dtype=int32, numpy=
array([[1, 0, 1],
       [0, 1, 1],
       [0, 0, 1],
       [0, 0, 1],
       [0, 0, 1],
       [0, 1, 0]], dtype=int32)>

Jeżeli nazywamy prob (ma taki sam semantykę kształt jak log_prob ; używamy prob z tych małych przykładów Bernoulliego dla przejrzystości, ale log_prob zwykle preferowane w aplikacjach) można przekazać go wektor i ocena prawdopodobieństwa każdej monety plonowania, że wartość :

b3.prob([1, 1, 0])

<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.29999998, 0.5       , 0.29999998], dtype=float32)>

Dlaczego API zawiera kształt partii? Semantycznie, można wykonywać te same obliczenia, tworząc listę dystrybucji i iteracji nad nimi z for pętli (przynajmniej w trybie Eager, w trybie wykresu TF którą trzeba tf.while pętlę). Jednak posiadanie (potencjalnie dużego) zestawu identycznie sparametryzowanych rozkładów jest niezwykle powszechne, a wykorzystanie obliczeń wektorowych, gdy tylko jest to możliwe, jest kluczowym elementem umożliwiającym wykonywanie szybkich obliczeń przy użyciu akceleratorów sprzętowych.

Używanie niezależnych do agregowania partii do zdarzeń

W poprzednim rozdziale stworzyliśmy b3 , jeden Distribution obiekt, który reprezentował trzy monety koziołki. Jeśli nazwaliśmy b3.prob na wektorze \(v\)The \(i\)„th wejście było prawdopodobieństwo, że \(i\)th monetę bierze wartość \(v[i]\).

Załóżmy, że zamiast tego chcielibyśmy określić „łączny” rozkład niezależnych zmiennych losowych z tej samej podstawowej rodziny. To jest inny obiekt matematycznie, że dla tej nowej dystrybucji, prob na wektorze \(v\) powróci pojedynczej wartości reprezentującej prawdopodobieństwo, że cały zestaw monet odpowiada wektor \(v\).

Jak to robimy? Używamy „wyższego rzędu” dystrybucji o nazwie Independent , który odbywa się rozkład i daje w wyniku nowego rozkładu z kształtem partii przeniósł się do kształtu wydarzeniu:

b3_joint = tfd.Independent(b3, reinterpreted_batch_ndims=1)
b3_joint

<tfp.distributions.Independent 'IndependentBernoulli' batch_shape=[] event_shape=[3] dtype=int32>

Porównaj kształt oryginalnego b3 :

b3

<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[3] event_shape=[] dtype=int32>

Zgodnie z obietnicą, widzimy, że Independent przeniósł kształt wsadowy w kształcie zdarzeń: b3_joint jest pojedynczym dystrybucja ( batch_shape = () ) w trójwymiarowej przestrzeni zdarzeń ( event_shape = (3,) ).

Sprawdźmy semantykę:

b3_joint.prob([1, 1, 0])

<tf.Tensor: shape=(), dtype=float32, numpy=0.044999998>

Alternatywny sposób, aby uzyskać ten sam rezultat byłoby prawdopodobieństw obliczeniowych przy użyciu b3 i zrobić redukcję ręcznie poprzez pomnożenie (lub, w bardziej typowym przypadku gdy stosowane są prawdopodobieństwa dziennika, zsumowanie):

tf.reduce_prod(b3.prob([1, 1, 0]))

<tf.Tensor: shape=(), dtype=float32, numpy=0.044999994>

Indpendent pozwala użytkownikowi bardziej wyraźnie stanowią pożądany koncepcji. Uważamy to za niezwykle przydatne, chociaż nie jest to bezwzględnie konieczne.

Zabawne fakty:

b3.sample i b3_joint.sample mają różne implementacje koncepcyjne, ale wyjścia nie do odróżnienia: różnicę między partii niezależnych rozkładów i pojedynczym dystrybucji utworzonym z partii za pomocą Independent pojawia się przy obliczaniu probabilites, nie podczas pobierania próbek.
MultivariateNormalDiag może być trywialnie realizowane z wykorzystaniem skalarne Normal i Independent rozkładów (nie jest faktycznie realizowany w ten sposób, ale to może być).

Partie dystrybucji wielowymiarowych

Utwórzmy zbiór trzech dwuwymiarowych wielowymiarowych normalnych o pełnej kowariancji:

nd_batch = tfd.MultivariateNormalFullCovariance(
    loc = [[0., 0.], [1., 1.], [2., 2.]],
    covariance_matrix = [[[1., .1], [.1, 1.]], 
                         [[1., .3], [.3, 1.]],
                         [[1., .5], [.5, 1.]]])
nd_batch

<tfp.distributions.MultivariateNormalFullCovariance 'MultivariateNormalFullCovariance' batch_shape=[3] event_shape=[2] dtype=float32>

Widzimy batch_shape = (3,) , tak, że są trzy niezależne wielowymiarowe normalne i event_shape = (2,) , tak aby każdy wielowymiarowa normalnie jest dwuwymiarowy. W tym przykładzie poszczególne dystrybucje nie mają niezależnych elementów.

Próbkowanie działa:

nd_batch.sample(4)

<tf.Tensor: shape=(4, 3, 2), dtype=float32, numpy=
array([[[ 0.7367498 ,  2.730996  ],
        [-0.74080074, -0.36466932],
        [ 0.6516018 ,  0.9391426 ]],

       [[ 1.038303  ,  0.12231752],
        [-0.94788766, -1.204232  ],
        [ 4.059758  ,  3.035752  ]],

       [[ 0.56903946, -0.06875849],
        [-0.35127294,  0.5311631 ],
        [ 3.4635801 ,  4.565582  ]],

       [[-0.15989424, -0.25715637],
        [ 0.87479895,  0.97391707],
        [ 0.5211419 ,  2.32108   ]]], dtype=float32)>

Od batch_shape = (3,) i event_shape = (2,) , przechodzimy tensora kształtu (3, 2) do log_prob :

nd_batch.log_prob([[0., 0.], [1., 1.], [2., 2.]])

<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.8328519, -1.7907217, -1.694036 ], dtype=float32)>

Nadawanie, czyli dlaczego jest to takie zagmatwane?

Abstrahując się, co zrobiliśmy do tej pory, każda dystrybucja ma kształt partii B i kształt wydarzenie E . Pozwolić BE być połączeniem kształtów zdarzeń:

Dla rozkładu jednowymiarowych skalarnych n i b , BE = (). .
Dla dwuwymiarowych wielowymiarowych normalnych nd . BE = (2).
Zarówno w b3 i b3_joint , BE = (3).
Dla partii wielowymiarowych normalnych ndb , BE = (3, 2).

„Zasady oceny”, z których korzystaliśmy do tej pory, to:

Próbka bez argumentu zwraca tensor w kształcie BE ; próbkowania ze skalarnym n zwrotów „N o BE ” napinającej.
prob i log_prob wziąć tensor kształcie BE i zwrócić wynik kształt B .

Rzeczywista „zasada oceny” dla prob i log_prob jest bardziej skomplikowana, w sposób, który oferuje potencjalną siłę i szybkość, ale także złożoności i wyzwań. Rzeczywista zasadą jest (zasadniczo), który argument do log_prob musi broadcastable na BE ; wszelkie „dodatkowe” wymiary są zachowywane w danych wyjściowych.

Przyjrzyjmy się implikacjom. Dla jednoczynnikowej normalnego n , BE = () , tak log_prob oczekuje skalarnych. Jeśli mijamy log_prob tensora z niepustym kształtu, te pojawiają się jako wymiary wsadowych na wyjściu:

n = tfd.Normal(loc=0., scale=1.)
n

<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>

n.log_prob(0.)

<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>

n.log_prob([0.])

<tf.Tensor: shape=(1,), dtype=float32, numpy=array([-0.9189385], dtype=float32)>

n.log_prob([[0., 1.], [-1., 2.]])

<tf.Tensor: shape=(2, 2), dtype=float32, numpy=
array([[-0.9189385, -1.4189385],
       [-1.4189385, -2.9189386]], dtype=float32)>

Kolej na dwuwymiarowym wieloczynnikowej normalnego Chodźmy nd (parametry zmienione dla celów poglądowych):

nd = tfd.MultivariateNormalDiag(loc=[0., 1.], scale_diag=[1., 1.])
nd

<tfp.distributions.MultivariateNormalDiag 'MultivariateNormalDiag' batch_shape=[] event_shape=[2] dtype=float32>

log_prob „oczekuje” argument z kształtu (2,) , ale będzie to zaakceptować żadnego argumentu, że transmisje przeciwko tym kształcie:

nd.log_prob([0., 0.])

<tf.Tensor: shape=(), dtype=float32, numpy=-2.337877>

Ale możemy przechodzić w „Więcej” przykładach i ocenić wszystkie swoje log_prob „s na raz:

nd.log_prob([[0., 0.],
             [1., 1.],
             [2., 2.]])

<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-2.337877 , -2.337877 , -4.3378773], dtype=float32)>

Być może mniej przekonująco, możemy transmitować w wymiarach wydarzenia:

nd.log_prob([0.])

<tf.Tensor: shape=(), dtype=float32, numpy=-2.337877>

nd.log_prob([[0.], [1.], [2.]])

<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-2.337877 , -2.337877 , -4.3378773], dtype=float32)>

Nadawanie w ten sposób jest konsekwencją naszego projektu „umożliwiaj nadawanie zawsze, gdy to możliwe”; to użycie jest nieco kontrowersyjne i potencjalnie może zostać usunięte w przyszłej wersji TFP.

Teraz spójrzmy ponownie na przykład trzech monet:

b3 = tfd.Bernoulli(probs=[.3, .5, .7])

Tutaj, przy użyciu transmisji reprezentuje prawdopodobieństwo, że każda moneta podchodzi głowy jest dość intuicyjny:

b3.prob([1])

<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.29999998, 0.5       , 0.7       ], dtype=float32)>

(Porównaj to b3.prob([1., 1., 1.]) , które użyliśmy tam, gdzie b3 został wprowadzony).

Załóżmy teraz, że chcemy wiedzieć, dla każdej monety, prawdopodobieństwo moneta podchodzi głowy, a prawdopodobieństwo, że pojawia się ogony. Możemy sobie wyobrazić próbowanie:

b3.log_prob([0, 1])

Niestety powoduje to błąd z długim i mało czytelnym śladem stosu. b3 ma BE = (3) , więc musimy zdać b3.prob coś broadcastable przeciwko (3,) . [0, 1] ma kształt (2) , więc nie nadaje i tworzy błąd. Zamiast tego musimy powiedzieć:

b3.prob([[0], [1]])

<tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[0.7, 0.5, 0.3],
       [0.3, 0.5, 0.7]], dtype=float32)>

Czemu? [[0], [1]] ma kształt (2, 1) , tak, że transmisje na kształt (3) , aby kształt nadawanych (2, 3) .

Transmisja jest dość potężna: istnieją przypadki, w których pozwala na zmniejszenie o rząd wielkości ilości używanej pamięci i często skraca kod użytkownika. Jednak programowanie może być trudne. Jeśli zadzwonisz log_prob i pojawia się błąd, zaniechanie nadawania jest prawie zawsze problem.

Idąc dalej

W tym samouczku przedstawiliśmy (miejmy nadzieję) proste wprowadzenie. Kilka wskazówek, aby przejść dalej:

event_shape , batch_shape i sample_shape może być dowolna pozycja (w tym poradniku są zawsze albo skalar lub pozycja 1). Zwiększa to moc, ale znowu może prowadzić do wyzwań programowych, zwłaszcza gdy zaangażowane jest nadawanie. Za dodatkową głębokiego nurkowania w manipulacji kształt, zobacz Understanding TensorFlow rozkładów Kształty .
TFP zawiera silny poboru zwany Bijectors , które w połączeniu z TransformedDistribution , daje elastyczną, kompozycyjną sposób łatwo utworzyć nowy rozkład, który jest odwracalna przemiany istniejących dystrybucji. Spróbujemy napisać poradnik o tym wkrótce, ale w międzyczasie, sprawdź dokumentację