Mục đích của máy tính xách tay này là giúp TFP 0.12.1 "trở nên sống động" thông qua một số đoạn mã nhỏ - bản trình diễn nhỏ về những thứ bạn có thể đạt được với TFP.
 Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
Cài đặt và nhập
!pip3 install -qU tensorflow==2.4.0 tensorflow_probability==0.12.1 tensorflow-datasets inference_gym
import tensorflow as tf
import tensorflow_probability as tfp
assert '0.12' in tfp.__version__, tfp.__version__
assert '2.4' in tf.__version__, tf.__version__
physical_devices = tf.config.list_physical_devices('CPU')
tf.config.set_logical_device_configuration(
physical_devices[0],
[tf.config.LogicalDeviceConfiguration(),
tf.config.LogicalDeviceConfiguration()])
tfd = tfp.distributions
tfb = tfp.bijectors
tfpk = tfp.math.psd_kernels
import matplotlib.pyplot as plt
import numpy as np
import scipy.interpolate
import IPython
import seaborn as sns
from inference_gym import using_tensorflow as gym
import logging
Bijector
Glow
Một bijector từ giấy Glow: Generative luồng với khả nghịch 1x1 nhiều nếp cuộn , bởi Kingma và Dhariwal.
Đây là cách vẽ một hình ảnh từ một bản phân phối (lưu ý rằng bản phân phối chưa "học" gì ở đây).
image_shape = (32, 32, 4) # 32 x 32 RGBA image
glow = tfb.Glow(output_shape=image_shape,
coupling_bijector_fn=tfb.GlowDefaultNetwork,
exit_bijector_fn=tfb.GlowDefaultExitNetwork)
pz = tfd.Sample(tfd.Normal(0., 1.), tf.reduce_prod(image_shape))
# Calling glow on distribution p(z) creates our glow distribution over images.
px = glow(pz)
# Take samples from the distribution to get images from your dataset.
image = px.sample(1)[0].numpy()
# Rescale to [0, 1].
image = (image - image.min()) / (image.max() - image.min())
plt.imshow(image);

RayleighCDF
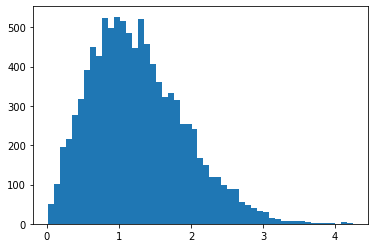
Bijector cho phân phối của Rayleigh CDF. Một cách sử dụng là lấy mẫu từ phân bố Rayleigh, bằng cách lấy các mẫu đồng nhất, sau đó chuyển chúng qua nghịch đảo của CDF.
bij = tfb.RayleighCDF()
uniforms = tfd.Uniform().sample(10_000)
plt.hist(bij.inverse(uniforms), bins='auto');
Ascending() thay thế Invert(Ordered())
x = tfd.Normal(0., 1.).sample(5)
print(tfb.Ascending()(x))
print(tfb.Invert(tfb.Ordered())(x))
tf.Tensor([1.9363368 2.650928 3.4936204 4.1817293 5.6920815], shape=(5,), dtype=float32) WARNING:tensorflow:From <ipython-input-5-1406b9939c00>:3: Ordered.__init__ (from tensorflow_probability.python.bijectors.ordered) is deprecated and will be removed after 2021-01-09. Instructions for updating: `Ordered` bijector is deprecated; please use `tfb.Invert(tfb.Ascending())` instead. tf.Tensor([1.9363368 2.650928 3.4936204 4.1817293 5.6920815], shape=(5,), dtype=float32)
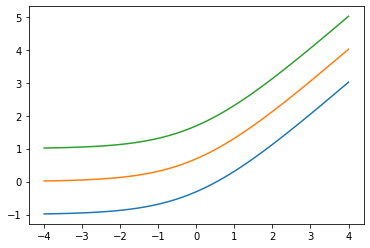
Thêm low arg: Softplus(low=2.)
x = tf.linspace(-4., 4., 100)
for low in (-1., 0., 1.):
bij = tfb.Softplus(low=low)
plt.plot(x, bij(x));
tfb.ScaleMatvecLinearOperatorBlock hỗ trợ blockwise LinearOperator , args đa phần
op_1 = tf.linalg.LinearOperatorDiag(diag=[1., -1., 3.])
op_2 = tf.linalg.LinearOperatorFullMatrix([[12., 5.], [-1., 3.]])
scale = tf.linalg.LinearOperatorBlockDiag([op_1, op_2], is_non_singular=True)
bij = tfb.ScaleMatvecLinearOperatorBlock(scale)
bij([[1., 2., 3.], [0., 1.]])
WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow/python/ops/linalg/linear_operator_block_diag.py:223: LinearOperator.graph_parents (from tensorflow.python.ops.linalg.linear_operator) is deprecated and will be removed in a future version. Instructions for updating: Do not call `graph_parents`. [<tf.Tensor: shape=(3,), dtype=float32, numpy=array([ 1., -2., 9.], dtype=float32)>, <tf.Tensor: shape=(2,), dtype=float32, numpy=array([5., 3.], dtype=float32)>]
Phân phối
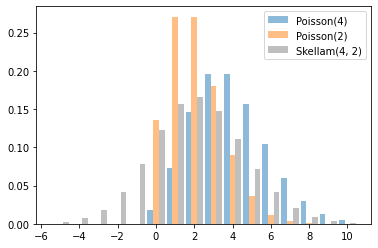
Skellam
Phân phối trên sự khác biệt của hai Poisson RVs. Lưu ý rằng các mẫu từ phân phối này có thể âm tính.
x = tf.linspace(-5., 10., 10 - -5 + 1)
rates = (4, 2)
for i, rate in enumerate(rates):
plt.bar(x - .3 * (1 - i), tfd.Poisson(rate).prob(x), label=f'Poisson({rate})', alpha=0.5, width=.3)
plt.bar(x.numpy() + .3, tfd.Skellam(*rates).prob(x).numpy(), color='k', alpha=0.25, width=.3,
label=f'Skellam{rates}')
plt.legend();
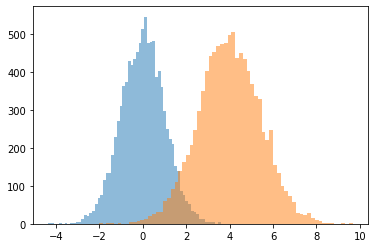
JointDistributionCoroutine[AutoBatched] sản namedtuple -like mẫu
Định rõ sample_dtype=[...] cho người cao tuổi tuple hành vi.
@tfd.JointDistributionCoroutineAutoBatched
def model():
x = yield tfd.Normal(0., 1., name='x')
y = x + 4.
yield tfd.Normal(y, 1., name='y')
draw = model.sample(10_000)
plt.hist(draw.x, bins='auto', alpha=0.5)
plt.hist(draw.y, bins='auto', alpha=0.5);
WARNING:tensorflow:Note that RandomStandardNormal inside pfor op may not give same output as inside a sequential loop. WARNING:tensorflow:Note that RandomStandardNormal inside pfor op may not give same output as inside a sequential loop.
VonMisesFisher hỗ trợ dim > 5 , entropy()
Các phân phối von Mises-Fisher là một phân phối trên \(n-1\) cầu chiều trong \(\mathbb{R}^n\).
dist = tfd.VonMisesFisher([0., 1, 0, 1, 0, 1], concentration=1.)
draws = dist.sample(3)
print(dist.entropy())
tf.reduce_sum(draws ** 2, axis=1) # each draw has length 1
tf.Tensor(3.3533673, shape=(), dtype=float32) <tf.Tensor: shape=(3,), dtype=float32, numpy=array([1.0000002 , 0.99999994, 1.0000001 ], dtype=float32)>
ExpGamma , ExpInverseGamma
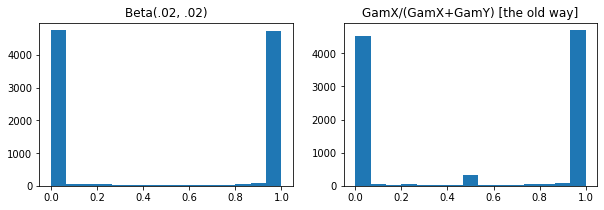
log_rate tham số thêm vào Gamma . Cải tiến số khi-nồng độ thấp lấy mẫu Beta , Dirichlet và bạn bè. Các gradient đại diện lại ngầm định trong mọi trường hợp.
plt.figure(figsize=(10, 3))
plt.subplot(121)
plt.hist(tfd.Beta(.02, .02).sample(10_000), bins='auto')
plt.title('Beta(.02, .02)')
plt.subplot(122)
plt.title('GamX/(GamX+GamY) [the old way]')
g = tfd.Gamma(.02, 1); s0, s1 = g.sample(10_000), g.sample(10_000)
plt.hist(s0 / (s0 + s1), bins='auto')
plt.show()
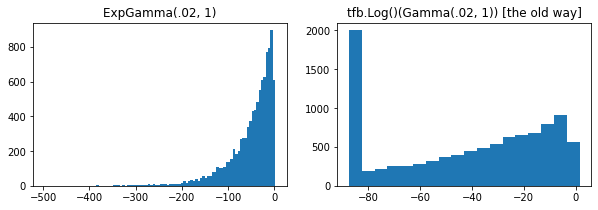
plt.figure(figsize=(10, 3))
plt.subplot(121)
plt.hist(tfd.ExpGamma(.02, 1.).sample(10_000), bins='auto')
plt.title('ExpGamma(.02, 1)')
plt.subplot(122)
plt.hist(tfb.Log()(tfd.Gamma(.02, 1.)).sample(10_000), bins='auto')
plt.title('tfb.Log()(Gamma(.02, 1)) [the old way]');
JointDistribution*AutoBatched hỗ trợ lấy mẫu tái sản xuất (với chiều dài-2 tuple / hạt tensor)
@tfd.JointDistributionCoroutineAutoBatched
def model():
x = yield tfd.Normal(0, 1, name='x')
y = yield tfd.Normal(x + 4, 1, name='y')
print(model.sample(seed=(1, 2)))
print(model.sample(seed=(1, 2)))
StructTuple( x=<tf.Tensor: shape=(), dtype=float32, numpy=-0.59835213>, y=<tf.Tensor: shape=(), dtype=float32, numpy=6.2380724> ) StructTuple( x=<tf.Tensor: shape=(), dtype=float32, numpy=-0.59835213>, y=<tf.Tensor: shape=(), dtype=float32, numpy=6.2380724> )
KL(VonMisesFisher || SphericalUniform)
# Build vMFs with the same mean direction, batch of increasing concentrations.
vmf = tfd.VonMisesFisher(tf.math.l2_normalize(tf.random.normal([10])),
concentration=[0., .1, 1., 10.])
# KL increases with concentration, since vMF(conc=0) == SphericalUniform.
print(tfd.kl_divergence(vmf, tfd.SphericalUniform(10)))
tf.Tensor([4.7683716e-07 4.9877167e-04 4.9384594e-02 2.4844694e+00], shape=(4,), dtype=float32)
parameter_properties
Lớp phân phối tại phơi bày một parameter_properties(dtype=tf.float32, num_classes=None) phương pháp lớp học, có thể cho phép xây dựng tự động của nhiều loại phân phối.
print('Gamma:', tfd.Gamma.parameter_properties())
print('Categorical:', tfd.Categorical.parameter_properties(dtype=tf.float64, num_classes=7))
Gamma: {'concentration': ParameterProperties(event_ndims=0, shape_fn=<function ParameterProperties.<lambda> at 0x7ff6bbfcdd90>, default_constraining_bijector_fn=<function Gamma._parameter_properties.<locals>.<lambda> at 0x7ff6afd95510>, is_preferred=True), 'rate': ParameterProperties(event_ndims=0, shape_fn=<function ParameterProperties.<lambda> at 0x7ff6bbfcdd90>, default_constraining_bijector_fn=<function Gamma._parameter_properties.<locals>.<lambda> at 0x7ff6afd95ea0>, is_preferred=False), 'log_rate': ParameterProperties(event_ndims=0, shape_fn=<function ParameterProperties.<lambda> at 0x7ff6bbfcdd90>, default_constraining_bijector_fn=<class 'tensorflow_probability.python.bijectors.identity.Identity'>, is_preferred=True)}
Categorical: {'logits': ParameterProperties(event_ndims=1, shape_fn=<function Categorical._parameter_properties.<locals>.<lambda> at 0x7ff6afd95510>, default_constraining_bijector_fn=<class 'tensorflow_probability.python.bijectors.identity.Identity'>, is_preferred=True), 'probs': ParameterProperties(event_ndims=1, shape_fn=<function Categorical._parameter_properties.<locals>.<lambda> at 0x7ff6afdc91e0>, default_constraining_bijector_fn=<class 'tensorflow_probability.python.bijectors.softmax_centered.SoftmaxCentered'>, is_preferred=False)}
experimental_default_event_space_bijector
Bây giờ chấp nhận các args bổ sung ghim một số bộ phận phân phối.
@tfd.JointDistributionCoroutineAutoBatched
def model():
scale = yield tfd.Gamma(1, 1, name='scale')
obs = yield tfd.Normal(0, scale, name='obs')
model.experimental_default_event_space_bijector(obs=.2).forward(
[tf.random.uniform([3], -2, 2.)])
StructTuple( scale=<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.6630705, 1.5401832, 1.0777743], dtype=float32)> )
JointDistribution.experimental_pin
Pins một số bộ phận phân phối chung, trở JointDistributionPinned đối tượng đại diện cho mật độ unnormalized doanh.
Làm việc với experimental_default_event_space_bijector , điều này làm cho việc làm suy luận variational hoặc MCMC với giá trị mặc định hợp lý đơn giản hơn nhiều. Trong bên dưới Ví dụ, hai dòng đầu tiên của sample làm chạy MCMC một làn gió.
dist = tfd.JointDistributionSequential([
tfd.HalfNormal(1.),
lambda scale: tfd.Normal(0., scale, name='observed')])
@tf.function
def sample():
bij = dist.experimental_default_event_space_bijector(observed=1.)
target_log_prob = dist.experimental_pin(observed=1.).unnormalized_log_prob
kernel = tfp.mcmc.TransformedTransitionKernel(
tfp.mcmc.HamiltonianMonteCarlo(target_log_prob,
step_size=0.6,
num_leapfrog_steps=16),
bijector=bij)
return tfp.mcmc.sample_chain(500,
current_state=tf.ones([8]), # multiple chains
kernel=kernel,
trace_fn=None)
draws = sample()
fig, (hist, trace) = plt.subplots(ncols=2, figsize=(16, 3))
trace.plot(draws, alpha=0.5)
for col in tf.transpose(draws):
sns.kdeplot(col, ax=hist);
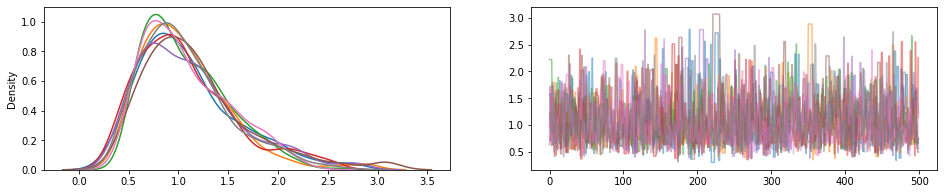
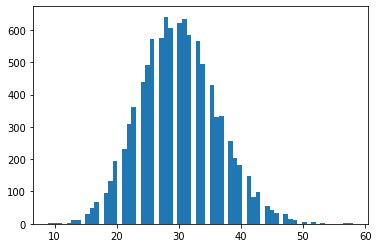
tfd.NegativeBinomial.experimental_from_mean_dispersion
Tham số thay thế. Gửi email tới tfprobability@tensorflow.org hoặc gửi PR cho chúng tôi để thêm các phương thức lớp tương tự cho các bản phân phối khác.
nb = tfd.NegativeBinomial.experimental_from_mean_dispersion(30., .01)
plt.hist(nb.sample(10_000), bins='auto');
tfp.experimental.distribute
DistributionStrategy -aware phân phối chung, cho phép tính toán khả năng trên nhiều thiết bị. Sharded Independent và Sample phân phối.
# Note: 2-logical devices are configured in the install/import cell at top.
strategy = tf.distribute.MirroredStrategy()
assert strategy.num_replicas_in_sync == 2
@tfp.experimental.distribute.JointDistributionCoroutine
def model():
root = tfp.experimental.distribute.JointDistributionCoroutine.Root
group_scale = yield root(tfd.Sample(tfd.Exponential(1), 3, name='group_scale'))
_ = yield tfp.experimental.distribute.ShardedSample(tfd.Independent(tfd.Normal(0, group_scale), 1),
sample_shape=[4], name='x')
seed1, seed2 = tfp.random.split_seed((1, 2))
@tf.function
def sample(seed):
return model.sample(seed=seed)
xs = strategy.run(sample, (seed1,))
print("""
Note that the global latent `group_scale` is shared across devices, whereas
the local `x` is sampled independently on each device.
""")
print('sample:', xs)
print('another sample:', strategy.run(sample, (seed2,)))
@tf.function
def log_prob(x):
return model.log_prob(x)
print("""
Note that each device observes the same log_prob (local latent log_probs are
summed across devices).
""")
print('log_prob:', strategy.run(log_prob, (xs,)))
@tf.function
def grad_log_prob(x):
return tfp.math.value_and_gradient(model.log_prob, x)[1]
print("""
Note that each device observes the same log_prob gradient (local latents have
independent gradients, global latents have gradients aggregated across devices).
""")
print('grad_log_prob:', strategy.run(grad_log_prob, (xs,)))
WARNING:tensorflow:There are non-GPU devices in `tf.distribute.Strategy`, not using nccl allreduce.
INFO:tensorflow:Using MirroredStrategy with devices ('/job:localhost/replica:0/task:0/device:CPU:0', '/job:localhost/replica:0/task:0/device:CPU:1')
Note that the global latent `group_scale` is shared across devices, whereas
the local `x` is sampled independently on each device.
sample: StructTuple(
group_scale=PerReplica:{
0: <tf.Tensor: shape=(3,), dtype=float32, numpy=array([2.6355493, 1.1805456, 1.245112 ], dtype=float32)>,
1: <tf.Tensor: shape=(3,), dtype=float32, numpy=array([2.6355493, 1.1805456, 1.245112 ], dtype=float32)>
},
x=PerReplica:{
0: <tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[-0.90548456, 0.7675636 , 0.27627748],
[-0.3475989 , 2.0194046 , -1.2531326 ]], dtype=float32)>,
1: <tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[ 3.251305 , -0.5790973 , 0.42745453],
[-1.562331 , 0.3006323 , 0.635732 ]], dtype=float32)>
}
)
another sample: StructTuple(
group_scale=PerReplica:{
0: <tf.Tensor: shape=(3,), dtype=float32, numpy=array([2.41133 , 0.10307606, 0.5236566 ], dtype=float32)>,
1: <tf.Tensor: shape=(3,), dtype=float32, numpy=array([2.41133 , 0.10307606, 0.5236566 ], dtype=float32)>
},
x=PerReplica:{
0: <tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[-3.2476294 , 0.07213175, -0.39536062],
[-1.2319602 , -0.05505352, 0.06356457]], dtype=float32)>,
1: <tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[ 5.6028705 , 0.11919801, -0.48446828],
[-1.5938259 , 0.21123725, 0.28979057]], dtype=float32)>
}
)
Note that each device observes the same log_prob (local latent log_probs are
summed across devices).
INFO:tensorflow:Reduce to /job:localhost/replica:0/task:0/device:CPU:0 then broadcast to ('/job:localhost/replica:0/task:0/device:CPU:0', '/job:localhost/replica:0/task:0/device:CPU:1').
log_prob: PerReplica:{
0: tf.Tensor(-25.05747, shape=(), dtype=float32),
1: tf.Tensor(-25.05747, shape=(), dtype=float32)
}
Note that each device observes the same log_prob gradient (local latents have
independent gradients, global latents are aggregated across devices).
INFO:tensorflow:Reduce to /job:localhost/replica:0/task:0/device:CPU:0 then broadcast to ('/job:localhost/replica:0/task:0/device:CPU:0', '/job:localhost/replica:0/task:0/device:CPU:1').
INFO:tensorflow:Reduce to /job:localhost/replica:0/task:0/device:CPU:0 then broadcast to ('/job:localhost/replica:0/task:0/device:CPU:0', '/job:localhost/replica:0/task:0/device:CPU:1').
grad_log_prob: StructTuple(
group_scale=PerReplica:{
0: <tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.7555585, -1.2928739, -3.0554674], dtype=float32)>,
1: <tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.7555585, -1.2928739, -3.0554674], dtype=float32)>
},
x=PerReplica:{
0: <tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[ 0.13035832, -0.5507428 , -0.17820862],
[ 0.05004217, -1.4489648 , 0.80831426]], dtype=float32)>,
1: <tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[-0.46807498, 0.41551432, -0.27572307],
[ 0.22492138, -0.21570992, -0.41006932]], dtype=float32)>
}
)
Nhân PSD
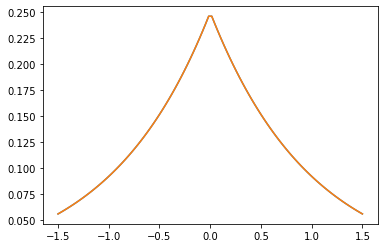
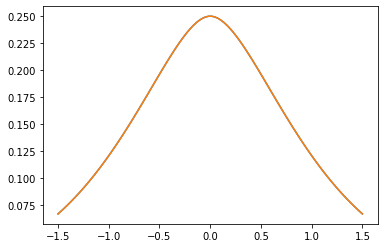
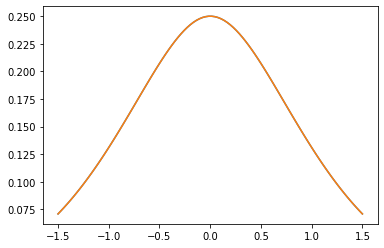
GeneralizedMatern
Các GeneralizedMatern dương-semidefinite kernel khái quát MaternOneHalf , MAterhThreeHalves , và MaternFiveHalves .
gm = tfpk.GeneralizedMatern(df=[0.5, 1.5, 2.5], length_scale=1., amplitude=0.5)
m1 = tfpk.MaternOneHalf(length_scale=1., amplitude=0.5)
m2 = tfpk.MaternThreeHalves(length_scale=1., amplitude=0.5)
m3 = tfpk.MaternFiveHalves(length_scale=1., amplitude=0.5)
xs = tf.linspace(-1.5, 1.5, 100)
gm_matrix = gm.matrix([[0.]], xs[..., tf.newaxis])
plt.plot(xs, gm_matrix[0][0])
plt.plot(xs, m1.matrix([[0.]], xs[..., tf.newaxis])[0])
plt.show()
plt.plot(xs, gm_matrix[1][0])
plt.plot(xs, m2.matrix([[0.]], xs[..., tf.newaxis])[0])
plt.show()
plt.plot(xs, gm_matrix[2][0])
plt.plot(xs, m3.matrix([[0.]], xs[..., tf.newaxis])[0])
plt.show()
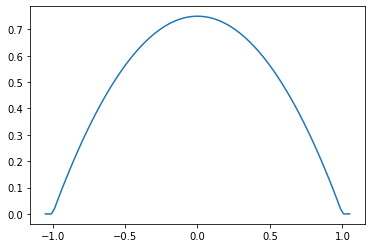
Parabolic (Epanechnikov)
epa = tfpk.Parabolic()
xs = tf.linspace(-1.05, 1.05, 100)
plt.plot(xs, epa.matrix([[0.]], xs[..., tf.newaxis])[0]);
VI
build_asvi_surrogate_posterior
Tự động tạo phần sau đại diện có cấu trúc cho VI theo cách kết hợp với cấu trúc đồ họa của bản phân phối trước. Này sử dụng phương pháp mô tả trong giấy tự động có cấu trúc biến phân Suy luận ( https://arxiv.org/abs/2002.00643 ).
# Import a Brownian Motion model from TFP's inference gym.
model = gym.targets.BrownianMotionMissingMiddleObservations()
prior = model.prior_distribution()
ground_truth = ground_truth = model.sample_transformations['identity'].ground_truth_mean
target_log_prob = lambda *values: model.log_likelihood(values) + prior.log_prob(values)
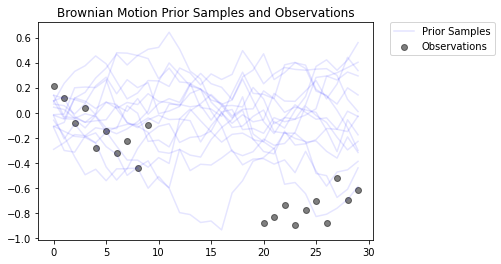
Điều này mô hình hóa quá trình Chuyển động Brown với mô hình quan sát Gaussian. Nó bao gồm 30 bước thời gian, nhưng 10 bước ở giữa là không thể quan sát được.
locs[0] ~ Normal(loc=0, scale=innovation_noise_scale)
for t in range(1, num_timesteps):
locs[t] ~ Normal(loc=locs[t - 1], scale=innovation_noise_scale)
for t in range(num_timesteps):
observed_locs[t] ~ Normal(loc=locs[t], scale=observation_noise_scale)
Mục đích là để suy ra các giá trị của locs từ những quan sát ồn ào ( observed_locs ). Kể từ giữa 10 timesteps là không quan sát được, observed_locs là NaN giá trị tại timesteps [10,19].
# The observed loc values in the Brownian Motion inference gym model
OBSERVED_LOC = np.array([
0.21592641, 0.118771404, -0.07945447, 0.037677474, -0.27885845, -0.1484156,
-0.3250906, -0.22957903, -0.44110894, -0.09830782, np.nan, np.nan, np.nan,
np.nan, np.nan, np.nan, np.nan, np.nan, np.nan, np.nan, -0.8786016,
-0.83736074, -0.7384849, -0.8939254, -0.7774566, -0.70238715, -0.87771565,
-0.51853573, -0.6948214, -0.6202789
]).astype(dtype=np.float32)
# Plot the prior and the likelihood observations
plt.figure()
plt.title('Brownian Motion Prior Samples and Observations')
num_samples = 15
prior_samples = prior.sample(num_samples)
plt.plot(prior_samples, c='blue', alpha=0.1)
plt.plot(prior_samples[0][0], label="Prior Samples", c='blue', alpha=0.1)
plt.scatter(x=range(30),y=OBSERVED_LOC, c='black', alpha=0.5, label="Observations")
plt.legend(bbox_to_anchor=(1.05, 1), borderaxespad=0.);
logging.getLogger('tensorflow').setLevel(logging.ERROR) # suppress pfor warnings
# Construct and train an ASVI Surrogate Posterior.
asvi_surrogate_posterior = tfp.experimental.vi.build_asvi_surrogate_posterior(prior)
asvi_losses = tfp.vi.fit_surrogate_posterior(target_log_prob,
asvi_surrogate_posterior,
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=500)
logging.getLogger('tensorflow').setLevel(logging.NOTSET)
# Construct and train a Mean-Field Surrogate Posterior.
factored_surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(event_shape=prior.event_shape)
factored_losses = tfp.vi.fit_surrogate_posterior(target_log_prob,
factored_surrogate_posterior,
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=500)
logging.getLogger('tensorflow').setLevel(logging.ERROR) # suppress pfor warnings
# Sample from the posteriors.
asvi_posterior_samples = asvi_surrogate_posterior.sample(num_samples)
factored_posterior_samples = factored_surrogate_posterior.sample(num_samples)
logging.getLogger('tensorflow').setLevel(logging.NOTSET)
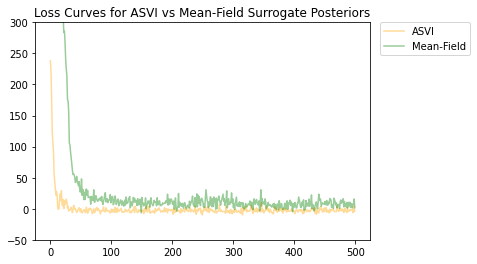
Cả ASVI và phân bố phía sau đại diện trường trung bình đều đã hội tụ, và phần sau đại diện ASVI có tổn thất cuối cùng thấp hơn (giá trị ELBO âm).
# Plot the loss curves.
plt.figure()
plt.title('Loss Curves for ASVI vs Mean-Field Surrogate Posteriors')
plt.plot(asvi_losses, c='orange', label='ASVI', alpha = 0.4)
plt.plot(factored_losses, c='green', label='Mean-Field', alpha = 0.4)
plt.ylim(-50, 300)
plt.legend(bbox_to_anchor=(1.3, 1), borderaxespad=0.);
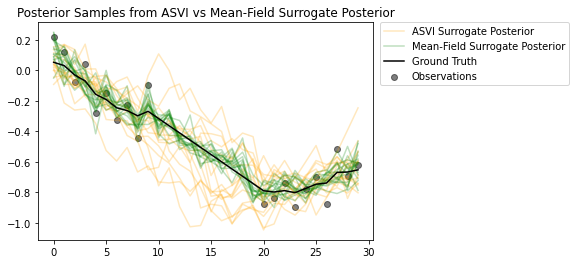
Các mẫu từ phần sau làm nổi bật phần sau đại diện ASVI nắm bắt độ không đảm bảo đối với các bước thời gian mà không cần quan sát độc đáo như thế nào. Mặt khác, phần sau đại diện trường trung bình đấu tranh để nắm bắt sự không chắc chắn thực sự.
# Plot samples from the ASVI and Mean-Field Surrogate Posteriors.
plt.figure()
plt.title('Posterior Samples from ASVI vs Mean-Field Surrogate Posterior')
plt.plot(asvi_posterior_samples, c='orange', alpha = 0.25)
plt.plot(asvi_posterior_samples[0][0], label='ASVI Surrogate Posterior', c='orange', alpha = 0.25)
plt.plot(factored_posterior_samples, c='green', alpha = 0.25)
plt.plot(factored_posterior_samples[0][0], label='Mean-Field Surrogate Posterior', c='green', alpha = 0.25)
plt.scatter(x=range(30),y=OBSERVED_LOC, c='black', alpha=0.5, label='Observations')
plt.plot(ground_truth, c='black', label='Ground Truth')
plt.legend(bbox_to_anchor=(1.585, 1), borderaxespad=0.);
MCMC
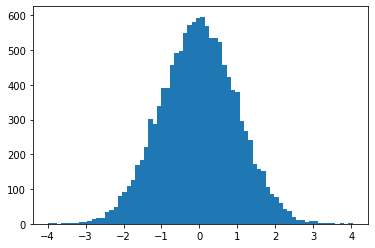
ProgressBarReducer
Hình dung tiến trình của bộ lấy mẫu. (Có thể có một hình phạt hiệu suất danh nghĩa; hiện không được hỗ trợ theo biên dịch JIT.)
kernel = tfp.mcmc.HamiltonianMonteCarlo(lambda x: -x**2 / 2, .05, 20)
pbar = tfp.experimental.mcmc.ProgressBarReducer(100)
kernel = tfp.experimental.mcmc.WithReductions(kernel, pbar)
plt.hist(tf.reshape(tfp.mcmc.sample_chain(100, current_state=tf.ones([128]), kernel=kernel, trace_fn=None), [-1]), bins='auto')
pbar.bar.close()
99%|█████████▉| 99/100 [00:03<00:00, 27.37it/s]
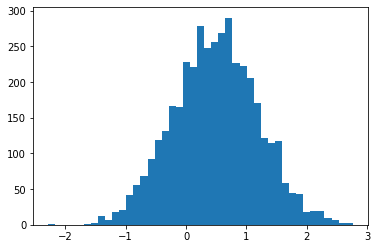
sample_sequential_monte_carlo hỗ trợ lấy mẫu tái sản xuất
initial_state = tf.random.uniform([4096], -2., 2.)
def smc(seed):
return tfp.experimental.mcmc.sample_sequential_monte_carlo(
prior_log_prob_fn=lambda x: -x**2 / 2,
likelihood_log_prob_fn=lambda x: -(x-1.)**2 / 2,
current_state=initial_state,
seed=seed)[1]
plt.hist(smc(seed=(12, 34)), bins='auto');plt.show()
print(smc(seed=(12, 34))[:10])
print('different:', smc(seed=(10, 20))[:10])
print('same:', smc(seed=(12, 34))[:10])
tf.Tensor( [ 0.665834 0.9892149 0.7961128 1.0016634 -1.000767 -0.19461267 1.3070581 1.127177 0.9940303 0.58239716], shape=(10,), dtype=float32) different: tf.Tensor( [ 1.3284367 0.4374407 1.1349089 0.4557473 0.06510283 -0.08954388 1.1735026 0.8170528 0.12443061 0.34413314], shape=(10,), dtype=float32) same: tf.Tensor( [ 0.665834 0.9892149 0.7961128 1.0016634 -1.000767 -0.19461267 1.3070581 1.127177 0.9940303 0.58239716], shape=(10,), dtype=float32)
Đã thêm tính toán phát trực tuyến của phương sai, hiệp phương sai, Rhat
Lưu ý, các giao diện để những đã thay đổi một chút trong tfp-nightly .
def cov_to_ellipse(t, cov, mean):
"""Draw a one standard deviation ellipse from the mean, according to cov."""
diag = tf.linalg.diag_part(cov)
a = 0.5 * tf.reduce_sum(diag)
b = tf.sqrt(0.25 * (diag[0] - diag[1])**2 + cov[0, 1]**2)
major = a + b
minor = a - b
theta = tf.math.atan2(major - cov[0, 0], cov[0, 1])
x = (tf.sqrt(major) * tf.cos(theta) * tf.cos(t) -
tf.sqrt(minor) * tf.sin(theta) * tf.sin(t))
y = (tf.sqrt(major) * tf.sin(theta) * tf.cos(t) +
tf.sqrt(minor) * tf.cos(theta) * tf.sin(t))
return x + mean[0], y + mean[1]
fig, axes = plt.subplots(nrows=4, ncols=5, figsize=(14, 8),
sharex=True, sharey=True, constrained_layout=True)
t = tf.linspace(0., 2 * np.pi, 200)
tot = 10
cov = 0.1 * tf.eye(2) + 0.9 * tf.ones([2, 2])
mvn = tfd.MultivariateNormalTriL(loc=[1., 2.],
scale_tril=tf.linalg.cholesky(cov))
for ax in axes.ravel():
rv = tfp.experimental.stats.RunningCovariance(
num_samples=0., mean=tf.zeros(2), sum_squared_residuals=tf.zeros((2, 2)),
event_ndims=1)
for idx, x in enumerate(mvn.sample(tot)):
rv = rv.update(x)
ax.plot(*cov_to_ellipse(t, rv.covariance(), rv.mean),
color='k', alpha=(idx + 1) / tot)
ax.plot(*cov_to_ellipse(t, mvn.covariance(), mvn.mean()), 'r')
fig.suptitle("Twenty tries to approximate the red covariance with 10 draws");

Toán học, số liệu thống kê
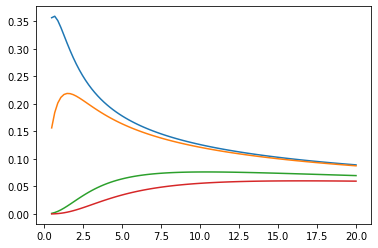
Các hàm Bessel: ive, kve, log-ive
xs = tf.linspace(0.5, 20., 100)
ys = tfp.math.bessel_ive([[0.5], [1.], [np.pi], [4.]], xs)
zs = tfp.math.bessel_kve([[0.5], [1.], [2.], [np.pi]], xs)
for i in range(4):
plt.plot(xs, ys[i])
plt.show()
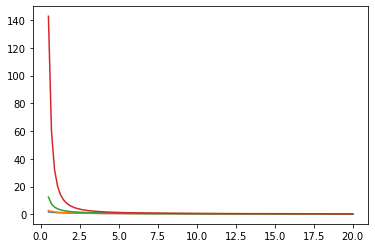
for i in range(4):
plt.plot(xs, zs[i])
plt.show()
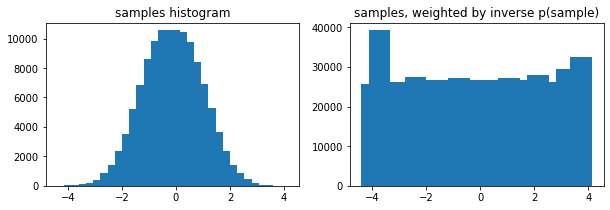
Tùy chọn weights arg để tfp.stats.histogram
edges = tf.linspace(-4., 4, 31)
samps = tfd.TruncatedNormal(0, 1, -4, 4).sample(100_000, seed=(123, 456))
_, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 3))
ax1.bar(edges[:-1], tfp.stats.histogram(samps, edges))
ax1.set_title('samples histogram')
ax2.bar(edges[:-1], tfp.stats.histogram(samps, edges, weights=1 / tfd.Normal(0, 1).prob(samps)))
ax2.set_title('samples, weighted by inverse p(sample)');
tfp.math.erfcinv
x = tf.linspace(-3., 3., 10)
y = tf.math.erfc(x)
z = tfp.math.erfcinv(y)
print(x)
print(z)
tf.Tensor( [-3. -2.3333333 -1.6666666 -1. -0.33333325 0.3333335 1. 1.666667 2.3333335 3. ], shape=(10,), dtype=float32) tf.Tensor( [-3.0002644 -2.3333426 -1.6666666 -0.9999997 -0.3333332 0.33333346 0.9999999 1.6666667 2.3333335 3.0000002 ], shape=(10,), dtype=float32)
