TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
Bu not defteri, yapısal zaman serisi (STS) modelleriyle uyum ve tahmin yaparken (Gauss dışı) bir gözlem modelini birleştirmek için TFP yaklaşık çıkarım araçlarının kullanımını gösterir. Bu örnekte, ayrık sayım verileriyle çalışmak için bir Poisson gözlem modeli kullanacağız.
import time
import matplotlib.pyplot as plt
import numpy as np
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd
tf.enable_v2_behavior()
Sentetik Veri
İlk önce bazı sentetik sayım verileri oluşturacağız:
num_timesteps = 30
observed_counts = np.round(3 + np.random.lognormal(np.log(np.linspace(
num_timesteps, 5, num=num_timesteps)), 0.20, size=num_timesteps))
observed_counts = observed_counts.astype(np.float32)
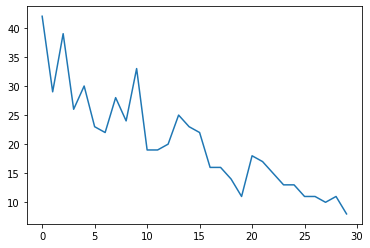
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f940ae958d0>]
modeli
Rastgele yürüyen doğrusal bir trend ile basit bir model belirleyeceğiz:
def build_model(approximate_unconstrained_rates):
trend = tfp.sts.LocalLinearTrend(
observed_time_series=approximate_unconstrained_rates)
return tfp.sts.Sum([trend],
observed_time_series=approximate_unconstrained_rates)
Bu model, gözlemlenen zaman serileri üzerinde çalışmak yerine, gözlemleri yöneten Poisson oranı parametreleri serisi üzerinde çalışacaktır.
Poisson oranları pozitif olması gerektiğinden, gerçek değerli STS modelini pozitif değerler üzerinden bir dağılıma dönüştürmek için bir bijektör kullanacağız. Softplus dönüşüm \(y = \log(1 + \exp(x))\) neredeyse pozitif değerler için doğrusal olduğu, doğal bir seçimdir, ancak bu gibi diğer seçenekler Exp (bir lognormal yürüyüş halinde normal rasgele yürüyüş dönüşümleri) da mümkündür.
positive_bijector = tfb.Softplus() # Or tfb.Exp()
# Approximate the unconstrained Poisson rate just to set heuristic priors.
# We could avoid this by passing explicit priors on all model params.
approximate_unconstrained_rates = positive_bijector.inverse(
tf.convert_to_tensor(observed_counts) + 0.01)
sts_model = build_model(approximate_unconstrained_rates)
Gauss olmayan bir gözlem modeli için yaklaşık çıkarımı kullanmak için, STS modelini bir TFP JointDistribution olarak kodlayacağız. Bu ortak dağılımdaki rastgele değişkenler, STS modelinin parametreleri, gizli Poisson oranlarının zaman serileri ve gözlemlenen sayılardır.
def sts_with_poisson_likelihood_model():
# Encode the parameters of the STS model as random variables.
param_vals = []
for param in sts_model.parameters:
param_val = yield param.prior
param_vals.append(param_val)
# Use the STS model to encode the log- (or inverse-softplus)
# rate of a Poisson.
unconstrained_rate = yield sts_model.make_state_space_model(
num_timesteps, param_vals)
rate = positive_bijector.forward(unconstrained_rate[..., 0])
observed_counts = yield tfd.Poisson(rate, name='observed_counts')
model = tfd.JointDistributionCoroutineAutoBatched(sts_with_poisson_likelihood_model)
çıkarım için hazırlık
Gözlenen sayılar göz önüne alındığında, modelde gözlemlenmeyen nicelikleri çıkarmak istiyoruz. İlk olarak, gözlemlenen sayımlarda ortak log yoğunluğunu koşullandırıyoruz.
pinned_model = model.experimental_pin(observed_counts=observed_counts)
Çıkarımın STS modelinin parametreleri üzerindeki kısıtlamalara uyduğundan emin olmak için kısıtlayıcı bir bijektöre de ihtiyacımız olacak (örneğin, ölçekler pozitif olmalıdır).
constraining_bijector = pinned_model.experimental_default_event_space_bijector()
HMC ile çıkarım
Model parametreleri ve gizli oranlar üzerinden eklem posteriorundan örnek almak için HMC'yi (özellikle, NUTS) kullanacağız.
Bu, standart bir STS modelinin HMC ile takılmasından önemli ölçüde daha yavaş olacaktır, çünkü modelin (nispeten az sayıda) parametrelerine ek olarak, Poisson oranlarının tüm serisini de çıkarmamız gerekir. Bu yüzden nispeten az sayıda adım için koşacağız; çıkarım kalitesinin kritik olduğu uygulamalar için bu değerleri artırmak veya birden çok zincir çalıştırmak mantıklı olabilir.
Örnekleyici yapılandırması
# Allow external control of sampling to reduce test runtimes.
num_results = 500 # @param { isTemplate: true}
num_results = int(num_results)
num_burnin_steps = 100 # @param { isTemplate: true}
num_burnin_steps = int(num_burnin_steps)
Önce bir Örnekleyiciyi belirtin ve ardından kullanmak sample_chain üretmek numunelerine o örnekleme çekirdeği çalıştırmak için.
sampler = tfp.mcmc.TransformedTransitionKernel(
tfp.mcmc.NoUTurnSampler(
target_log_prob_fn=pinned_model.unnormalized_log_prob,
step_size=0.1),
bijector=constraining_bijector)
adaptive_sampler = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=sampler,
num_adaptation_steps=int(0.8 * num_burnin_steps),
target_accept_prob=0.75)
initial_state = constraining_bijector.forward(
type(pinned_model.event_shape)(
*(tf.random.normal(part_shape)
for part_shape in constraining_bijector.inverse_event_shape(
pinned_model.event_shape))))
# Speed up sampling by tracing with `tf.function`.
@tf.function(autograph=False, jit_compile=True)
def do_sampling():
return tfp.mcmc.sample_chain(
kernel=adaptive_sampler,
current_state=initial_state,
num_results=num_results,
num_burnin_steps=num_burnin_steps,
trace_fn=None)
t0 = time.time()
samples = do_sampling()
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 24.83s.
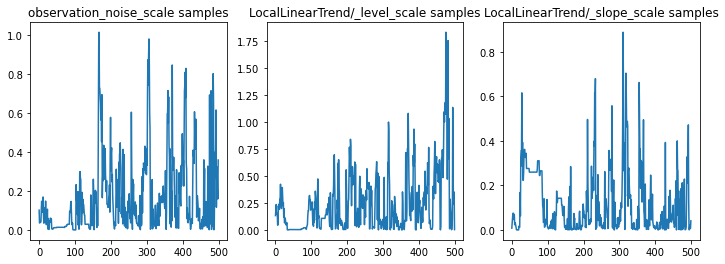
Parametre izlerini inceleyerek çıkarımı sağlıklı bir şekilde kontrol edebiliriz. Bu durumda, veriler için birden fazla açıklama araştırmış gibi görünüyorlar, ki bu iyidir, ancak daha fazla örnek, zincirin ne kadar iyi karıştığını yargılamak için yardımcı olacaktır.
f = plt.figure(figsize=(12, 4))
for i, param in enumerate(sts_model.parameters):
ax = f.add_subplot(1, len(sts_model.parameters), i + 1)
ax.plot(samples[i])
ax.set_title("{} samples".format(param.name))
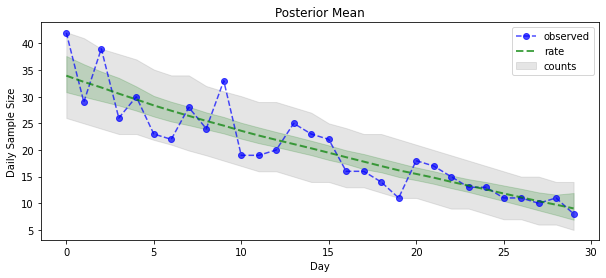
Şimdi getirisi için: Poisson oranlarının arkasını görelim! Ayrıca gözlemlenen sayımlar üzerinden %80 tahmin aralığını çizeceğiz ve bu aralığın gerçekten gözlemlediğimiz sayıların yaklaşık %80'ini içerdiğini kontrol edebiliriz.
param_samples = samples[:-1]
unconstrained_rate_samples = samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)
plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(np.random.poisson(rate_samples),
[10, 90], axis=0)
_ = plt.plot(observed_counts, color="blue", ls='--', marker='o', label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color="green", ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey', label='counts', alpha=0.2)
plt.xlabel("Day")
plt.ylabel("Daily Sample Size")
plt.title("Posterior Mean")
plt.legend()
<matplotlib.legend.Legend at 0x7f93ffd35550>
tahmin
Gözlenen sayıları tahmin etmek için, gizli oranlar üzerinde bir tahmin dağılımı oluşturmak için standart STS araçlarını kullanacağız (yine STS gerçek değerli verileri modellemek için tasarlandığından, kısıtlamasız uzayda), ardından örneklenen tahminleri bir Poisson gözleminden geçireceğiz. modeli:
def sample_forecasted_counts(sts_model, posterior_latent_rates,
posterior_params, num_steps_forecast,
num_sampled_forecasts):
# Forecast the future latent unconstrained rates, given the inferred latent
# unconstrained rates and parameters.
unconstrained_rates_forecast_dist = tfp.sts.forecast(sts_model,
observed_time_series=unconstrained_rate_samples,
parameter_samples=posterior_params,
num_steps_forecast=num_steps_forecast)
# Transform the forecast to positive-valued Poisson rates.
rates_forecast_dist = tfd.TransformedDistribution(
unconstrained_rates_forecast_dist,
positive_bijector)
# Sample from the forecast model following the chain rule:
# P(counts) = P(counts | latent_rates)P(latent_rates)
sampled_latent_rates = rates_forecast_dist.sample(num_sampled_forecasts)
sampled_forecast_counts = tfd.Poisson(rate=sampled_latent_rates).sample()
return sampled_forecast_counts, sampled_latent_rates
forecast_samples, rate_samples = sample_forecasted_counts(
sts_model,
posterior_latent_rates=unconstrained_rate_samples,
posterior_params=param_samples,
# Days to forecast:
num_steps_forecast=30,
num_sampled_forecasts=100)
forecast_samples = np.squeeze(forecast_samples)
def plot_forecast_helper(data, forecast_samples, CI=90):
"""Plot the observed time series alongside the forecast."""
plt.figure(figsize=(10, 4))
forecast_median = np.median(forecast_samples, axis=0)
num_steps = len(data)
num_steps_forecast = forecast_median.shape[-1]
plt.plot(np.arange(num_steps), data, lw=2, color='blue', linestyle='--', marker='o',
label='Observed Data', alpha=0.7)
forecast_steps = np.arange(num_steps, num_steps+num_steps_forecast)
CI_interval = [(100 - CI)/2, 100 - (100 - CI)/2]
lower, upper = np.percentile(forecast_samples, CI_interval, axis=0)
plt.plot(forecast_steps, forecast_median, lw=2, ls='--', marker='o', color='orange',
label=str(CI) + '% Forecast Interval', alpha=0.7)
plt.fill_between(forecast_steps,
lower,
upper, color='orange', alpha=0.2)
plt.xlim([0, num_steps+num_steps_forecast])
ymin, ymax = min(np.min(forecast_samples), np.min(data)), max(np.max(forecast_samples), np.max(data))
yrange = ymax-ymin
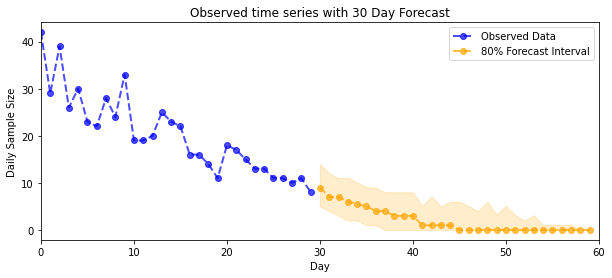
plt.title("{}".format('Observed time series with ' + str(num_steps_forecast) + ' Day Forecast'))
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
plt.legend()
plot_forecast_helper(observed_counts, forecast_samples, CI=80)
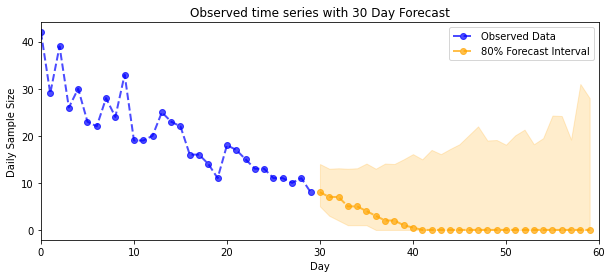
VI çıkarımı
(Standart STS modellerde olduğu gibi, bir zaman serisinin sadece parametreleri aksine) bizim yaklaşık sayıları gibi tam zamanlı dizi çıkarım yaparken Değişimsel çıkarım sorunlu olabilir. Değişkenlerin bağımsız posteriorlara sahip olduğu standart varsayımı oldukça yanlıştır, çünkü her bir zaman adımı komşuları ile ilişkilidir ve bu da belirsizliğin hafife alınmasına yol açabilir. Bu nedenle, tam zamanlı seriler üzerinden yaklaşık çıkarım için HMC daha iyi bir seçim olabilir. Ancak, VI biraz daha hızlı olabilir ve model prototipleme için veya performansının ampirik olarak 'yeterince iyi' olduğunun gösterilebildiği durumlarda faydalı olabilir.
Modelimizi VI'ya uydurmak için, bir vekil posterior oluşturup optimize ediyoruz:
surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
event_shape=pinned_model.event_shape,
bijector=constraining_bijector)
# Allow external control of optimization to reduce test runtimes.
num_variational_steps = 1000 # @param { isTemplate: true}
num_variational_steps = int(num_variational_steps)
t0 = time.time()
losses = tfp.vi.fit_surrogate_posterior(pinned_model.unnormalized_log_prob,
surrogate_posterior,
optimizer=tf.optimizers.Adam(0.1),
num_steps=num_variational_steps)
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 11.37s.
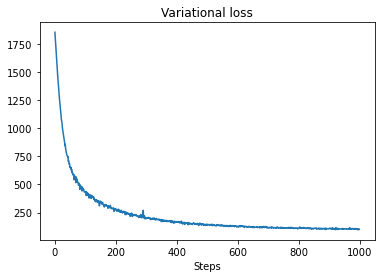
plt.plot(losses)
plt.title("Variational loss")
_ = plt.xlabel("Steps")
posterior_samples = surrogate_posterior.sample(50)
param_samples = posterior_samples[:-1]
unconstrained_rate_samples = posterior_samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)
plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(
np.random.poisson(rate_samples), [10, 90], axis=0)
_ = plt.plot(observed_counts, color='blue', ls='--', marker='o',
label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color='green',
ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(
np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey',
label='counts', alpha=0.2)
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
plt.title('Posterior Mean')
plt.legend()
<matplotlib.legend.Legend at 0x7f93ff4735c0>
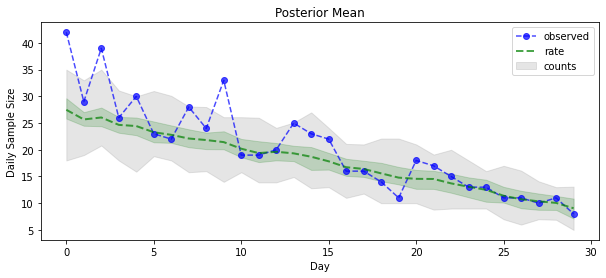
forecast_samples, rate_samples = sample_forecasted_counts(
sts_model,
posterior_latent_rates=unconstrained_rate_samples,
posterior_params=param_samples,
# Days to forecast:
num_steps_forecast=30,
num_sampled_forecasts=100)
forecast_samples = np.squeeze(forecast_samples)
plot_forecast_helper(observed_counts, forecast_samples, CI=80)