Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
Ten notatnik pokazuje zastosowanie narzędzi wnioskowania przybliżonego TFP do włączenia (niegaussowskiego) modelu obserwacji podczas dopasowywania i prognozowania za pomocą modeli strukturalnych szeregów czasowych (STS). W tym przykładzie użyjemy modelu obserwacji Poissona do pracy z dyskretnymi danymi zliczania.
import time
import matplotlib.pyplot as plt
import numpy as np
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd
tf.enable_v2_behavior()
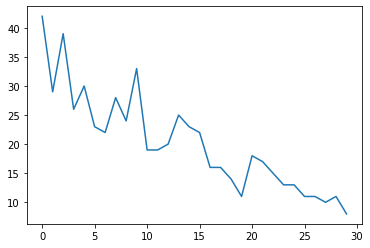
Dane syntetyczne
Najpierw wygenerujemy syntetyczne dane liczbowe:
num_timesteps = 30
observed_counts = np.round(3 + np.random.lognormal(np.log(np.linspace(
num_timesteps, 5, num=num_timesteps)), 0.20, size=num_timesteps))
observed_counts = observed_counts.astype(np.float32)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f940ae958d0>]
Model
Określimy prosty model z losowo chodzącym trendem liniowym:
def build_model(approximate_unconstrained_rates):
trend = tfp.sts.LocalLinearTrend(
observed_time_series=approximate_unconstrained_rates)
return tfp.sts.Sum([trend],
observed_time_series=approximate_unconstrained_rates)
Zamiast operować na obserwowanych szeregach czasowych, model ten będzie operował na szeregach parametrów współczynnika Poissona, które rządzą obserwacjami.
Ponieważ współczynniki Poissona muszą być dodatnie, użyjemy bijectora do przekształcenia modelu STS o wartościach rzeczywistych w rozkład na wartościach dodatnich. Softplus transformacja \(y = \log(1 + \exp(x))\) jest naturalnym wyborem, ponieważ jest prawie liniowa dla wartości dodatnich, ale inne opcje, takie jak Exp (który przekształca normalny losowy wchodzę do logarytmiczno-normalnego błądzenia losowego) są również możliwe.
positive_bijector = tfb.Softplus() # Or tfb.Exp()
# Approximate the unconstrained Poisson rate just to set heuristic priors.
# We could avoid this by passing explicit priors on all model params.
approximate_unconstrained_rates = positive_bijector.inverse(
tf.convert_to_tensor(observed_counts) + 0.01)
sts_model = build_model(approximate_unconstrained_rates)
Aby użyć przybliżonego wnioskowania dla niegaussowskiego modelu obserwacji, zakodujemy model STS jako TFP JointDistribution. Zmiennymi losowymi w tym łącznym rozkładzie są parametry modelu STS, szeregi czasowe utajonych współczynników Poissona oraz obserwowane liczebności.
def sts_with_poisson_likelihood_model():
# Encode the parameters of the STS model as random variables.
param_vals = []
for param in sts_model.parameters:
param_val = yield param.prior
param_vals.append(param_val)
# Use the STS model to encode the log- (or inverse-softplus)
# rate of a Poisson.
unconstrained_rate = yield sts_model.make_state_space_model(
num_timesteps, param_vals)
rate = positive_bijector.forward(unconstrained_rate[..., 0])
observed_counts = yield tfd.Poisson(rate, name='observed_counts')
model = tfd.JointDistributionCoroutineAutoBatched(sts_with_poisson_likelihood_model)
Przygotowanie do wnioskowania
Chcemy wywnioskować nieobserwowane wielkości w modelu, biorąc pod uwagę zaobserwowane liczby. Najpierw warunkujemy łączną gęstość logarytmiczną na obserwowanych zliczeniach.
pinned_model = model.experimental_pin(observed_counts=observed_counts)
Będziemy również potrzebować ograniczającego bijectora, aby upewnić się, że wnioskowanie uwzględnia ograniczenia parametrów modelu STS (na przykład skale muszą być dodatnie).
constraining_bijector = pinned_model.experimental_default_event_space_bijector()
Wnioskowanie z HMC
Użyjemy HMC (w szczególności NUTS) do pobierania próbek z tylnego stawu nad parametrami modelu i utajonymi współczynnikami.
Będzie to znacznie wolniejsze niż dopasowanie standardowego modelu STS z HMC, ponieważ oprócz parametrów modelu (stosunkowo małej liczby) musimy również wywnioskować całą serię współczynników Poissona. Pobiegniemy więc przez stosunkowo małą liczbę kroków; w przypadku aplikacji, w których jakość wnioskowania ma kluczowe znaczenie, sensowne może być zwiększenie tych wartości lub uruchomienie wielu łańcuchów.
Konfiguracja próbnika
# Allow external control of sampling to reduce test runtimes.
num_results = 500 # @param { isTemplate: true}
num_results = int(num_results)
num_burnin_steps = 100 # @param { isTemplate: true}
num_burnin_steps = int(num_burnin_steps)
Najpierw musimy określić sampler, a następnie użyj sample_chain do uruchomienia tego jądra próbkowania do próbek produktów.
sampler = tfp.mcmc.TransformedTransitionKernel(
tfp.mcmc.NoUTurnSampler(
target_log_prob_fn=pinned_model.unnormalized_log_prob,
step_size=0.1),
bijector=constraining_bijector)
adaptive_sampler = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=sampler,
num_adaptation_steps=int(0.8 * num_burnin_steps),
target_accept_prob=0.75)
initial_state = constraining_bijector.forward(
type(pinned_model.event_shape)(
*(tf.random.normal(part_shape)
for part_shape in constraining_bijector.inverse_event_shape(
pinned_model.event_shape))))
# Speed up sampling by tracing with `tf.function`.
@tf.function(autograph=False, jit_compile=True)
def do_sampling():
return tfp.mcmc.sample_chain(
kernel=adaptive_sampler,
current_state=initial_state,
num_results=num_results,
num_burnin_steps=num_burnin_steps,
trace_fn=None)
t0 = time.time()
samples = do_sampling()
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 24.83s.
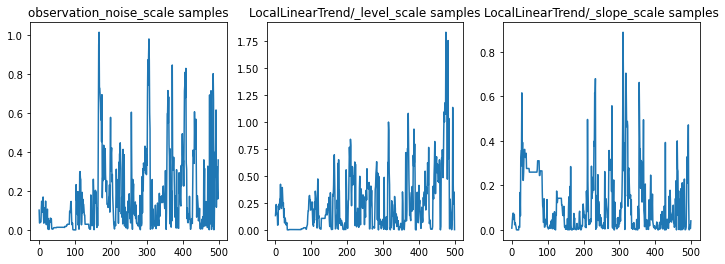
Możemy sprawdzić poprawność wnioskowania, badając ślady parametrów. W tym przypadku wydaje się, że zbadali wiele wyjaśnień danych, co jest dobre, chociaż więcej próbek byłoby pomocne w ocenie, jak dobrze miesza się łańcuch.
f = plt.figure(figsize=(12, 4))
for i, param in enumerate(sts_model.parameters):
ax = f.add_subplot(1, len(sts_model.parameters), i + 1)
ax.plot(samples[i])
ax.set_title("{} samples".format(param.name))
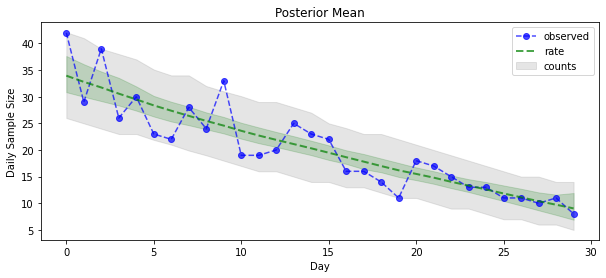
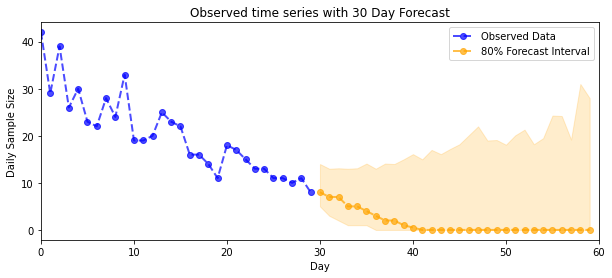
A teraz wypłata: przyjrzyjmy się później niż w przypadku wskaźników Poissona! Wykreślimy również 80% przedział predykcyjny dla zaobserwowanych liczebności i możemy sprawdzić, czy ten przedział zawiera około 80% liczebności, które faktycznie zaobserwowaliśmy.
param_samples = samples[:-1]
unconstrained_rate_samples = samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)
plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(np.random.poisson(rate_samples),
[10, 90], axis=0)
_ = plt.plot(observed_counts, color="blue", ls='--', marker='o', label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color="green", ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey', label='counts', alpha=0.2)
plt.xlabel("Day")
plt.ylabel("Daily Sample Size")
plt.title("Posterior Mean")
plt.legend()
<matplotlib.legend.Legend at 0x7f93ffd35550>
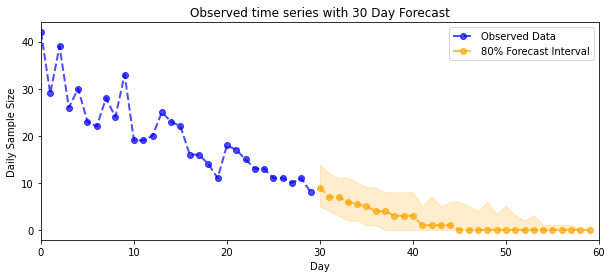
Prognozowanie
Aby prognozować obserwowane zliczenia, użyjemy standardowych narzędzi STS do zbudowania rozkładu prognozy na ukrytych współczynnikach (w nieograniczonej przestrzeni, ponownie, ponieważ STS jest przeznaczony do modelowania danych o wartościach rzeczywistych), a następnie przekażemy próbkowane prognozy przez obserwację Poissona Model:
def sample_forecasted_counts(sts_model, posterior_latent_rates,
posterior_params, num_steps_forecast,
num_sampled_forecasts):
# Forecast the future latent unconstrained rates, given the inferred latent
# unconstrained rates and parameters.
unconstrained_rates_forecast_dist = tfp.sts.forecast(sts_model,
observed_time_series=unconstrained_rate_samples,
parameter_samples=posterior_params,
num_steps_forecast=num_steps_forecast)
# Transform the forecast to positive-valued Poisson rates.
rates_forecast_dist = tfd.TransformedDistribution(
unconstrained_rates_forecast_dist,
positive_bijector)
# Sample from the forecast model following the chain rule:
# P(counts) = P(counts | latent_rates)P(latent_rates)
sampled_latent_rates = rates_forecast_dist.sample(num_sampled_forecasts)
sampled_forecast_counts = tfd.Poisson(rate=sampled_latent_rates).sample()
return sampled_forecast_counts, sampled_latent_rates
forecast_samples, rate_samples = sample_forecasted_counts(
sts_model,
posterior_latent_rates=unconstrained_rate_samples,
posterior_params=param_samples,
# Days to forecast:
num_steps_forecast=30,
num_sampled_forecasts=100)
forecast_samples = np.squeeze(forecast_samples)
def plot_forecast_helper(data, forecast_samples, CI=90):
"""Plot the observed time series alongside the forecast."""
plt.figure(figsize=(10, 4))
forecast_median = np.median(forecast_samples, axis=0)
num_steps = len(data)
num_steps_forecast = forecast_median.shape[-1]
plt.plot(np.arange(num_steps), data, lw=2, color='blue', linestyle='--', marker='o',
label='Observed Data', alpha=0.7)
forecast_steps = np.arange(num_steps, num_steps+num_steps_forecast)
CI_interval = [(100 - CI)/2, 100 - (100 - CI)/2]
lower, upper = np.percentile(forecast_samples, CI_interval, axis=0)
plt.plot(forecast_steps, forecast_median, lw=2, ls='--', marker='o', color='orange',
label=str(CI) + '% Forecast Interval', alpha=0.7)
plt.fill_between(forecast_steps,
lower,
upper, color='orange', alpha=0.2)
plt.xlim([0, num_steps+num_steps_forecast])
ymin, ymax = min(np.min(forecast_samples), np.min(data)), max(np.max(forecast_samples), np.max(data))
yrange = ymax-ymin
plt.title("{}".format('Observed time series with ' + str(num_steps_forecast) + ' Day Forecast'))
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
plt.legend()
plot_forecast_helper(observed_counts, forecast_samples, CI=80)
VI wnioskowanie
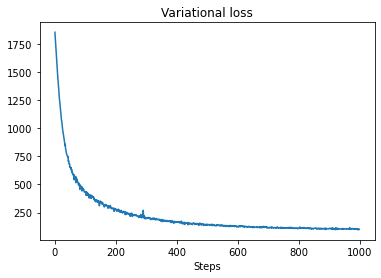
Wariacyjna wnioskowanie może być problematyczne, gdy wnioskowanie pełny szereg czasowy, jak nasze przybliżone liczby (w przeciwieństwie do zaledwie parametrów szeregu czasowego, jak w modelach STS standardowych). Standardowe założenie, że zmienne mają niezależne a posteriori jest całkiem błędne, ponieważ każdy krok czasowy jest skorelowany z sąsiadami, co może prowadzić do niedoszacowania niepewności. Z tego powodu konsola HMC może być lepszym wyborem do wnioskowania przybliżonego w pełnych szeregach czasowych. Jednak VI może być nieco szybszy i może być przydatny do prototypowania modeli lub w przypadkach, w których można empirycznie wykazać, że jego wydajność jest „wystarczająco dobra”.
Aby dopasować nasz model do VI, po prostu budujemy i optymalizujemy zastępczy tył:
surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
event_shape=pinned_model.event_shape,
bijector=constraining_bijector)
# Allow external control of optimization to reduce test runtimes.
num_variational_steps = 1000 # @param { isTemplate: true}
num_variational_steps = int(num_variational_steps)
t0 = time.time()
losses = tfp.vi.fit_surrogate_posterior(pinned_model.unnormalized_log_prob,
surrogate_posterior,
optimizer=tf.optimizers.Adam(0.1),
num_steps=num_variational_steps)
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 11.37s.
plt.plot(losses)
plt.title("Variational loss")
_ = plt.xlabel("Steps")
posterior_samples = surrogate_posterior.sample(50)
param_samples = posterior_samples[:-1]
unconstrained_rate_samples = posterior_samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)
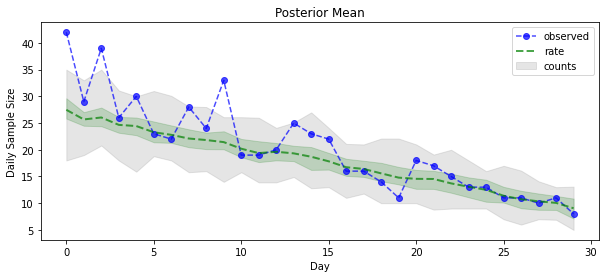
plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(
np.random.poisson(rate_samples), [10, 90], axis=0)
_ = plt.plot(observed_counts, color='blue', ls='--', marker='o',
label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color='green',
ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(
np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey',
label='counts', alpha=0.2)
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
plt.title('Posterior Mean')
plt.legend()
<matplotlib.legend.Legend at 0x7f93ff4735c0>
forecast_samples, rate_samples = sample_forecasted_counts(
sts_model,
posterior_latent_rates=unconstrained_rate_samples,
posterior_params=param_samples,
# Days to forecast:
num_steps_forecast=30,
num_sampled_forecasts=100)
forecast_samples = np.squeeze(forecast_samples)
plot_forecast_helper(observed_counts, forecast_samples, CI=80)