TensorFlow.org에서 보기 TensorFlow.org에서 보기 |  Google Colab에서 실행 Google Colab에서 실행 |  GitHub에서 소스 보기 GitHub에서 소스 보기 |  노트북 다운로드 노트북 다운로드 |
이 노트북은 구조적 시계열(STS) 모델로 피팅 및 예측할 때 (가우스가 아닌) 관찰 모델을 통합하기 위해 TFP 근사 추론 도구를 사용하는 방법을 보여줍니다. 이 예에서는 Poisson 관측 모델을 사용하여 불연속 카운트 데이터로 작업합니다.
import time
import matplotlib.pyplot as plt
import numpy as np
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd
tf.enable_v2_behavior()
합성 데이터
먼저 합성 카운트 데이터를 생성합니다.
num_timesteps = 30
observed_counts = np.round(3 + np.random.lognormal(np.log(np.linspace(
num_timesteps, 5, num=num_timesteps)), 0.20, size=num_timesteps))
observed_counts = observed_counts.astype(np.float32)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f940ae958d0>]
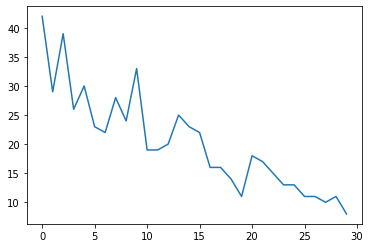
모델
무작위로 걷는 선형 추세가 있는 간단한 모델을 지정합니다.
def build_model(approximate_unconstrained_rates):
trend = tfp.sts.LocalLinearTrend(
observed_time_series=approximate_unconstrained_rates)
return tfp.sts.Sum([trend],
observed_time_series=approximate_unconstrained_rates)
관측된 시계열에서 작동하는 대신 이 모델은 관측을 제어하는 일련의 푸아송 비율 매개변수에서 작동합니다.
포아송 비율은 양수여야 하므로 바이젝터를 사용하여 실수 값 STS 모델을 양수 값에 대한 분포로 변환합니다. Softplus 변환 \(y = \log(1 + \exp(x))\) 이 양수 거의 선형이기 때문에, 자연 선택이지만, 예컨대 다른 선택 Exp (로그 정규 랜덤 워크로 통상 랜덤 워크 변환)도 가능하다.
positive_bijector = tfb.Softplus() # Or tfb.Exp()
# Approximate the unconstrained Poisson rate just to set heuristic priors.
# We could avoid this by passing explicit priors on all model params.
approximate_unconstrained_rates = positive_bijector.inverse(
tf.convert_to_tensor(observed_counts) + 0.01)
sts_model = build_model(approximate_unconstrained_rates)
가우스가 아닌 관찰 모델에 대한 근사 추론을 사용하기 위해 STS 모델을 TFP JointDistribution으로 인코딩합니다. 이 결합 분포의 확률 변수는 STS 모델의 매개변수, 잠재 포아송 비율의 시계열 및 관찰된 개수입니다.
def sts_with_poisson_likelihood_model():
# Encode the parameters of the STS model as random variables.
param_vals = []
for param in sts_model.parameters:
param_val = yield param.prior
param_vals.append(param_val)
# Use the STS model to encode the log- (or inverse-softplus)
# rate of a Poisson.
unconstrained_rate = yield sts_model.make_state_space_model(
num_timesteps, param_vals)
rate = positive_bijector.forward(unconstrained_rate[..., 0])
observed_counts = yield tfd.Poisson(rate, name='observed_counts')
model = tfd.JointDistributionCoroutineAutoBatched(sts_with_poisson_likelihood_model)
추론을 위한 준비
관찰된 개수가 주어지면 모델에서 관찰되지 않은 양을 추론하려고 합니다. 먼저 관찰된 카운트에 대한 조인트 로그 밀도를 조절합니다.
pinned_model = model.experimental_pin(observed_counts=observed_counts)
추론이 STS 모델의 매개변수에 대한 제약 조건을 준수하도록 하는 제약 바이젝터도 필요합니다(예: 척도는 양수여야 함).
constraining_bijector = pinned_model.experimental_default_event_space_bijector()
HMC로 추론
HMC(특히, NUTS)를 사용하여 모델 매개변수와 잠재율에 대한 후방 관절에서 샘플링합니다.
이것은 모델의 (상대적으로 적은 수의) 매개변수 외에도 전체 Poisson 비율 시리즈를 추론해야 하기 때문에 표준 STS 모델을 HMC에 맞추는 것보다 훨씬 느릴 것입니다. 따라서 우리는 비교적 적은 수의 단계를 실행할 것입니다. 추론 품질이 중요한 애플리케이션의 경우 이러한 값을 늘리거나 여러 체인을 실행하는 것이 합리적일 수 있습니다.
샘플러 구성
# Allow external control of sampling to reduce test runtimes.
num_results = 500 # @param { isTemplate: true}
num_results = int(num_results)
num_burnin_steps = 100 # @param { isTemplate: true}
num_burnin_steps = int(num_burnin_steps)
처음에 우리는 샘플러를 지정하고 사용하십시오 sample_chain 생산 샘플이 샘플링 커널을 실행합니다.
sampler = tfp.mcmc.TransformedTransitionKernel(
tfp.mcmc.NoUTurnSampler(
target_log_prob_fn=pinned_model.unnormalized_log_prob,
step_size=0.1),
bijector=constraining_bijector)
adaptive_sampler = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=sampler,
num_adaptation_steps=int(0.8 * num_burnin_steps),
target_accept_prob=0.75)
initial_state = constraining_bijector.forward(
type(pinned_model.event_shape)(
*(tf.random.normal(part_shape)
for part_shape in constraining_bijector.inverse_event_shape(
pinned_model.event_shape))))
# Speed up sampling by tracing with `tf.function`.
@tf.function(autograph=False, jit_compile=True)
def do_sampling():
return tfp.mcmc.sample_chain(
kernel=adaptive_sampler,
current_state=initial_state,
num_results=num_results,
num_burnin_steps=num_burnin_steps,
trace_fn=None)
t0 = time.time()
samples = do_sampling()
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 24.83s.
매개변수 추적을 검사하여 추론을 온전한 상태로 확인할 수 있습니다. 이 경우 그들은 데이터에 대한 여러 설명을 탐색한 것으로 보입니다. 이는 좋은 일이지만 더 많은 샘플이 체인이 얼마나 잘 혼합되고 있는지 판단하는 데 도움이 될 것입니다.
f = plt.figure(figsize=(12, 4))
for i, param in enumerate(sts_model.parameters):
ax = f.add_subplot(1, len(sts_model.parameters), i + 1)
ax.plot(samples[i])
ax.set_title("{} samples".format(param.name))
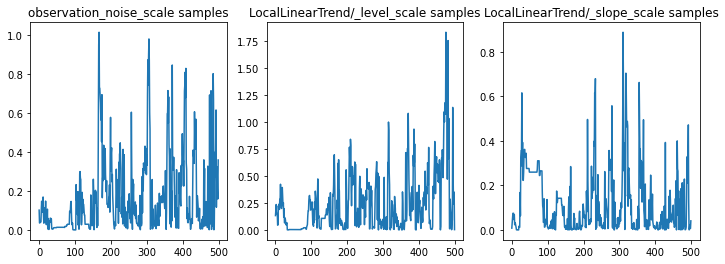
이제 보상을 위해: Poisson 비율에 대한 사후값을 봅시다! 또한 관찰된 개수에 대해 80% 예측 간격을 표시하고 이 간격에 실제로 관찰한 개수의 약 80%가 포함되어 있는지 확인할 수 있습니다.
param_samples = samples[:-1]
unconstrained_rate_samples = samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)
plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(np.random.poisson(rate_samples),
[10, 90], axis=0)
_ = plt.plot(observed_counts, color="blue", ls='--', marker='o', label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color="green", ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey', label='counts', alpha=0.2)
plt.xlabel("Day")
plt.ylabel("Daily Sample Size")
plt.title("Posterior Mean")
plt.legend()
<matplotlib.legend.Legend at 0x7f93ffd35550>
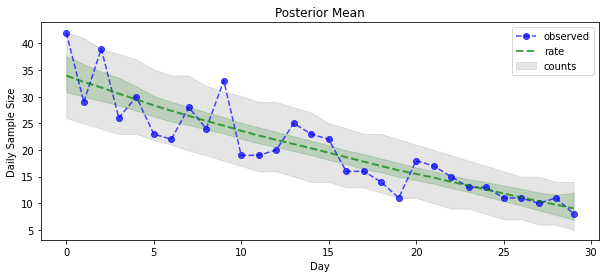
예측
관찰된 개수를 예측하기 위해 표준 STS 도구를 사용하여 잠재율에 대한 예측 분포를 구축한 다음(STS가 실제 값 데이터를 모델링하도록 설계되었으므로 다시 한 번 제약 없는 공간에서) 포아송 관찰을 통해 샘플링된 예측을 전달합니다. 모델:
def sample_forecasted_counts(sts_model, posterior_latent_rates,
posterior_params, num_steps_forecast,
num_sampled_forecasts):
# Forecast the future latent unconstrained rates, given the inferred latent
# unconstrained rates and parameters.
unconstrained_rates_forecast_dist = tfp.sts.forecast(sts_model,
observed_time_series=unconstrained_rate_samples,
parameter_samples=posterior_params,
num_steps_forecast=num_steps_forecast)
# Transform the forecast to positive-valued Poisson rates.
rates_forecast_dist = tfd.TransformedDistribution(
unconstrained_rates_forecast_dist,
positive_bijector)
# Sample from the forecast model following the chain rule:
# P(counts) = P(counts | latent_rates)P(latent_rates)
sampled_latent_rates = rates_forecast_dist.sample(num_sampled_forecasts)
sampled_forecast_counts = tfd.Poisson(rate=sampled_latent_rates).sample()
return sampled_forecast_counts, sampled_latent_rates
forecast_samples, rate_samples = sample_forecasted_counts(
sts_model,
posterior_latent_rates=unconstrained_rate_samples,
posterior_params=param_samples,
# Days to forecast:
num_steps_forecast=30,
num_sampled_forecasts=100)
forecast_samples = np.squeeze(forecast_samples)
def plot_forecast_helper(data, forecast_samples, CI=90):
"""Plot the observed time series alongside the forecast."""
plt.figure(figsize=(10, 4))
forecast_median = np.median(forecast_samples, axis=0)
num_steps = len(data)
num_steps_forecast = forecast_median.shape[-1]
plt.plot(np.arange(num_steps), data, lw=2, color='blue', linestyle='--', marker='o',
label='Observed Data', alpha=0.7)
forecast_steps = np.arange(num_steps, num_steps+num_steps_forecast)
CI_interval = [(100 - CI)/2, 100 - (100 - CI)/2]
lower, upper = np.percentile(forecast_samples, CI_interval, axis=0)
plt.plot(forecast_steps, forecast_median, lw=2, ls='--', marker='o', color='orange',
label=str(CI) + '% Forecast Interval', alpha=0.7)
plt.fill_between(forecast_steps,
lower,
upper, color='orange', alpha=0.2)
plt.xlim([0, num_steps+num_steps_forecast])
ymin, ymax = min(np.min(forecast_samples), np.min(data)), max(np.max(forecast_samples), np.max(data))
yrange = ymax-ymin
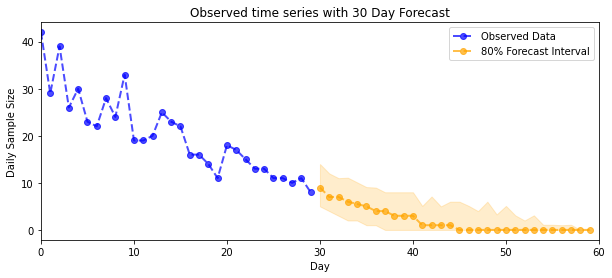
plt.title("{}".format('Observed time series with ' + str(num_steps_forecast) + ' Day Forecast'))
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
plt.legend()
plot_forecast_helper(observed_counts, forecast_samples, CI=80)
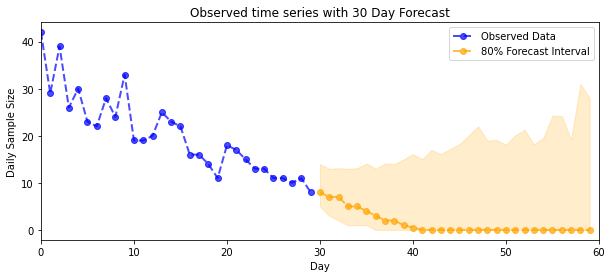
VI 추론
(표준 STS 모델로, 시계열의 단지 매개 변수와 달리) 우리의 대략적인 계산과 같은 풀 타임 시리즈를 추론 할 때 변화 적 추론 문제가 될 수 있습니다. 변수가 독립적인 사후값을 갖는다는 표준 가정은 매우 잘못된 것입니다. 각 시간 단계는 인접 항목과 상관 관계가 있어 불확실성을 과소평가할 수 있기 때문입니다. 이러한 이유로 HMC는 전체 시계열에 대한 근사 추론에 더 나은 선택일 수 있습니다. 그러나 VI는 훨씬 더 빠를 수 있으며 모델 프로토타이핑이나 성능이 경험적으로 '충분히 좋은' 것으로 나타날 수 있는 경우에 유용할 수 있습니다.
모델을 VI에 맞추기 위해 대리 사후 구조를 구축하고 최적화하기만 하면 됩니다.
surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
event_shape=pinned_model.event_shape,
bijector=constraining_bijector)
# Allow external control of optimization to reduce test runtimes.
num_variational_steps = 1000 # @param { isTemplate: true}
num_variational_steps = int(num_variational_steps)
t0 = time.time()
losses = tfp.vi.fit_surrogate_posterior(pinned_model.unnormalized_log_prob,
surrogate_posterior,
optimizer=tf.optimizers.Adam(0.1),
num_steps=num_variational_steps)
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 11.37s.
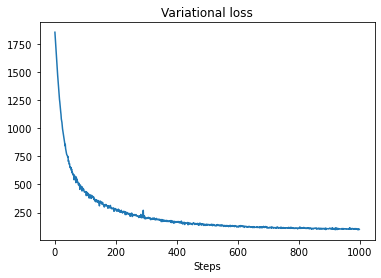
plt.plot(losses)
plt.title("Variational loss")
_ = plt.xlabel("Steps")
posterior_samples = surrogate_posterior.sample(50)
param_samples = posterior_samples[:-1]
unconstrained_rate_samples = posterior_samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)
plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(
np.random.poisson(rate_samples), [10, 90], axis=0)
_ = plt.plot(observed_counts, color='blue', ls='--', marker='o',
label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color='green',
ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(
np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey',
label='counts', alpha=0.2)
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
plt.title('Posterior Mean')
plt.legend()
<matplotlib.legend.Legend at 0x7f93ff4735c0>
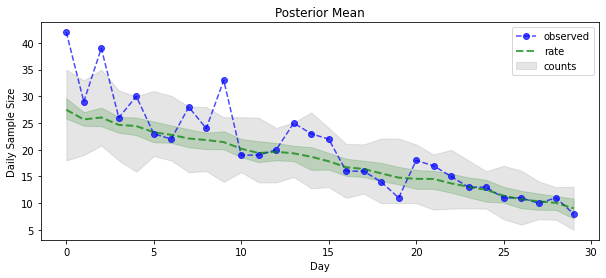
forecast_samples, rate_samples = sample_forecasted_counts(
sts_model,
posterior_latent_rates=unconstrained_rate_samples,
posterior_params=param_samples,
# Days to forecast:
num_steps_forecast=30,
num_sampled_forecasts=100)
forecast_samples = np.squeeze(forecast_samples)
plot_forecast_helper(observed_counts, forecast_samples, CI=80)