Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Ce cahier montre l'utilisation des outils d'inférence approximative de la PTF pour incorporer un modèle d'observation (non gaussien) lors de l'ajustement et de la prévision avec des modèles de séries temporelles structurelles (STS). Dans cet exemple, nous utiliserons un modèle d'observation de Poisson pour travailler avec des données de comptage discrètes.
import time
import matplotlib.pyplot as plt
import numpy as np
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd
tf.enable_v2_behavior()
Données synthétiques
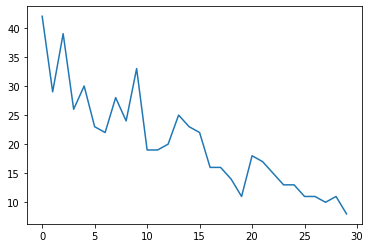
Nous allons d'abord générer des données de comptage synthétiques :
num_timesteps = 30
observed_counts = np.round(3 + np.random.lognormal(np.log(np.linspace(
num_timesteps, 5, num=num_timesteps)), 0.20, size=num_timesteps))
observed_counts = observed_counts.astype(np.float32)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f940ae958d0>]
Modèle
Nous allons spécifier un modèle simple avec une tendance linéaire à marche aléatoire :
def build_model(approximate_unconstrained_rates):
trend = tfp.sts.LocalLinearTrend(
observed_time_series=approximate_unconstrained_rates)
return tfp.sts.Sum([trend],
observed_time_series=approximate_unconstrained_rates)
Au lieu d'opérer sur les séries temporelles observées, ce modèle opérera sur les séries de paramètres du taux de Poisson qui régissent les observations.
Étant donné que les taux de Poisson doivent être positifs, nous utiliserons un bijecteur pour transformer le modèle STS à valeur réelle en une distribution sur des valeurs positives. La Softplus transformation \(y = \log(1 + \exp(x))\) est un choix naturel, car il est presque linéaire pour les valeurs positives, mais d' autres choix tels que Exp (qui transforme la marche aléatoire normale dans une marche aléatoire lognormal) sont également possibles.
positive_bijector = tfb.Softplus() # Or tfb.Exp()
# Approximate the unconstrained Poisson rate just to set heuristic priors.
# We could avoid this by passing explicit priors on all model params.
approximate_unconstrained_rates = positive_bijector.inverse(
tf.convert_to_tensor(observed_counts) + 0.01)
sts_model = build_model(approximate_unconstrained_rates)
Pour utiliser l'inférence approximative pour un modèle d'observation non gaussien, nous encoderons le modèle STS en tant que distribution conjointe TFP. Les variables aléatoires dans cette distribution conjointe sont les paramètres du modèle STS, la série chronologique des taux de Poisson latents et les dénombrements observés.
def sts_with_poisson_likelihood_model():
# Encode the parameters of the STS model as random variables.
param_vals = []
for param in sts_model.parameters:
param_val = yield param.prior
param_vals.append(param_val)
# Use the STS model to encode the log- (or inverse-softplus)
# rate of a Poisson.
unconstrained_rate = yield sts_model.make_state_space_model(
num_timesteps, param_vals)
rate = positive_bijector.forward(unconstrained_rate[..., 0])
observed_counts = yield tfd.Poisson(rate, name='observed_counts')
model = tfd.JointDistributionCoroutineAutoBatched(sts_with_poisson_likelihood_model)
Préparation à l'inférence
Nous voulons déduire les quantités non observées dans le modèle, étant donné les comptes observés. Tout d'abord, nous conditionnons la densité logarithmique conjointe sur les comptages observés.
pinned_model = model.experimental_pin(observed_counts=observed_counts)
Nous aurons également besoin d'un bijecteur contraignant pour s'assurer que l'inférence respecte les contraintes sur les paramètres du modèle STS (par exemple, les échelles doivent être positives).
constraining_bijector = pinned_model.experimental_default_event_space_bijector()
Inférence avec HMC
Nous utiliserons HMC (en particulier, NUTS) pour échantillonner à partir de la postérieure conjointe sur les paramètres du modèle et les taux de latence.
Cela sera nettement plus lent que d'ajuster un modèle STS standard avec HMC, car en plus des paramètres (relativement petit) du modèle, nous devons également déduire la série entière des taux de Poisson. Nous allons donc exécuter un nombre relativement petit d'étapes ; pour les applications où la qualité de l'inférence est critique, il peut être judicieux d'augmenter ces valeurs ou d'exécuter plusieurs chaînes.
Configuration de l'échantillonneur
# Allow external control of sampling to reduce test runtimes.
num_results = 500 # @param { isTemplate: true}
num_results = int(num_results)
num_burnin_steps = 100 # @param { isTemplate: true}
num_burnin_steps = int(num_burnin_steps)
D' abord , nous précisons un échantillonneur, puis utilisez sample_chain pour exécuter ce noyau d'échantillonnage pour produire des échantillons.
sampler = tfp.mcmc.TransformedTransitionKernel(
tfp.mcmc.NoUTurnSampler(
target_log_prob_fn=pinned_model.unnormalized_log_prob,
step_size=0.1),
bijector=constraining_bijector)
adaptive_sampler = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=sampler,
num_adaptation_steps=int(0.8 * num_burnin_steps),
target_accept_prob=0.75)
initial_state = constraining_bijector.forward(
type(pinned_model.event_shape)(
*(tf.random.normal(part_shape)
for part_shape in constraining_bijector.inverse_event_shape(
pinned_model.event_shape))))
# Speed up sampling by tracing with `tf.function`.
@tf.function(autograph=False, jit_compile=True)
def do_sampling():
return tfp.mcmc.sample_chain(
kernel=adaptive_sampler,
current_state=initial_state,
num_results=num_results,
num_burnin_steps=num_burnin_steps,
trace_fn=None)
t0 = time.time()
samples = do_sampling()
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 24.83s.
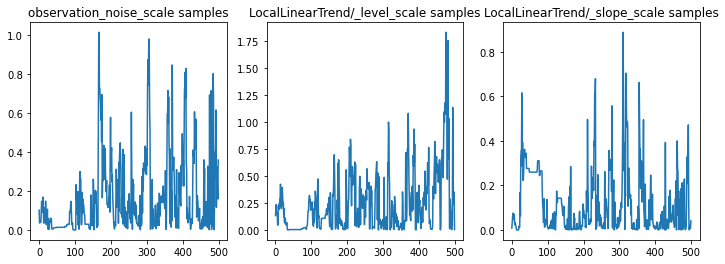
Nous pouvons vérifier l'inférence en examinant les traces des paramètres. Dans ce cas, ils semblent avoir exploré plusieurs explications pour les données, ce qui est bien, même si davantage d'échantillons seraient utiles pour juger de la qualité du mélange de la chaîne.
f = plt.figure(figsize=(12, 4))
for i, param in enumerate(sts_model.parameters):
ax = f.add_subplot(1, len(sts_model.parameters), i + 1)
ax.plot(samples[i])
ax.set_title("{} samples".format(param.name))
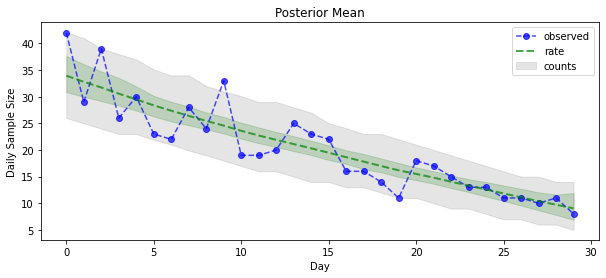
Maintenant pour le gain : voyons le postérieur sur les taux de Poisson ! Nous tracerons également l'intervalle prédictif de 80 % sur les dénombrements observés et pourrons vérifier que cet intervalle semble contenir environ 80 % des dénombrements que nous avons réellement observés.
param_samples = samples[:-1]
unconstrained_rate_samples = samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)
plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(np.random.poisson(rate_samples),
[10, 90], axis=0)
_ = plt.plot(observed_counts, color="blue", ls='--', marker='o', label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color="green", ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey', label='counts', alpha=0.2)
plt.xlabel("Day")
plt.ylabel("Daily Sample Size")
plt.title("Posterior Mean")
plt.legend()
<matplotlib.legend.Legend at 0x7f93ffd35550>
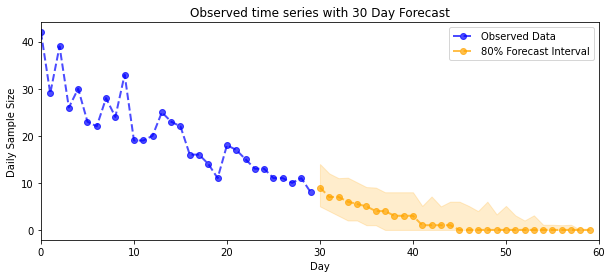
Prévision
Pour prévoir les dénombrements observés, nous utiliserons les outils STS standard pour créer une distribution de prévision sur les taux latents (dans un espace non contraint, encore une fois puisque STS est conçu pour modéliser des données à valeur réelle), puis passerons les prévisions échantillonnées à travers une observation de Poisson maquette:
def sample_forecasted_counts(sts_model, posterior_latent_rates,
posterior_params, num_steps_forecast,
num_sampled_forecasts):
# Forecast the future latent unconstrained rates, given the inferred latent
# unconstrained rates and parameters.
unconstrained_rates_forecast_dist = tfp.sts.forecast(sts_model,
observed_time_series=unconstrained_rate_samples,
parameter_samples=posterior_params,
num_steps_forecast=num_steps_forecast)
# Transform the forecast to positive-valued Poisson rates.
rates_forecast_dist = tfd.TransformedDistribution(
unconstrained_rates_forecast_dist,
positive_bijector)
# Sample from the forecast model following the chain rule:
# P(counts) = P(counts | latent_rates)P(latent_rates)
sampled_latent_rates = rates_forecast_dist.sample(num_sampled_forecasts)
sampled_forecast_counts = tfd.Poisson(rate=sampled_latent_rates).sample()
return sampled_forecast_counts, sampled_latent_rates
forecast_samples, rate_samples = sample_forecasted_counts(
sts_model,
posterior_latent_rates=unconstrained_rate_samples,
posterior_params=param_samples,
# Days to forecast:
num_steps_forecast=30,
num_sampled_forecasts=100)
forecast_samples = np.squeeze(forecast_samples)
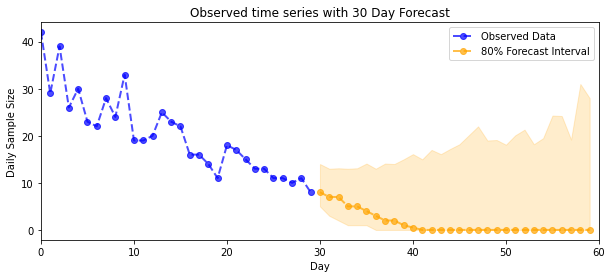
def plot_forecast_helper(data, forecast_samples, CI=90):
"""Plot the observed time series alongside the forecast."""
plt.figure(figsize=(10, 4))
forecast_median = np.median(forecast_samples, axis=0)
num_steps = len(data)
num_steps_forecast = forecast_median.shape[-1]
plt.plot(np.arange(num_steps), data, lw=2, color='blue', linestyle='--', marker='o',
label='Observed Data', alpha=0.7)
forecast_steps = np.arange(num_steps, num_steps+num_steps_forecast)
CI_interval = [(100 - CI)/2, 100 - (100 - CI)/2]
lower, upper = np.percentile(forecast_samples, CI_interval, axis=0)
plt.plot(forecast_steps, forecast_median, lw=2, ls='--', marker='o', color='orange',
label=str(CI) + '% Forecast Interval', alpha=0.7)
plt.fill_between(forecast_steps,
lower,
upper, color='orange', alpha=0.2)
plt.xlim([0, num_steps+num_steps_forecast])
ymin, ymax = min(np.min(forecast_samples), np.min(data)), max(np.max(forecast_samples), np.max(data))
yrange = ymax-ymin
plt.title("{}".format('Observed time series with ' + str(num_steps_forecast) + ' Day Forecast'))
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
plt.legend()
plot_forecast_helper(observed_counts, forecast_samples, CI=80)
VI inférence
Inférence variationnelle peut être problématique quand inférant une série à plein temps, comme nos chefs approximatifs (par opposition aux seuls paramètres d'une série chronologique, comme dans les modèles standards STS). L'hypothèse standard selon laquelle les variables ont des postérieurs indépendants est tout à fait erronée, car chaque pas de temps est corrélé avec ses voisins, ce qui peut conduire à sous-estimer l'incertitude. Pour cette raison, HMC peut être un meilleur choix pour l'inférence approximative sur des séries temporelles complètes. Cependant, VI peut être un peu plus rapide et peut être utile pour le prototypage de modèles ou dans les cas où ses performances peuvent être démontrées empiriquement comme « assez bonnes ».
Pour adapter notre modèle à VI, nous construisons et optimisons simplement un a posteriori de substitution :
surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
event_shape=pinned_model.event_shape,
bijector=constraining_bijector)
# Allow external control of optimization to reduce test runtimes.
num_variational_steps = 1000 # @param { isTemplate: true}
num_variational_steps = int(num_variational_steps)
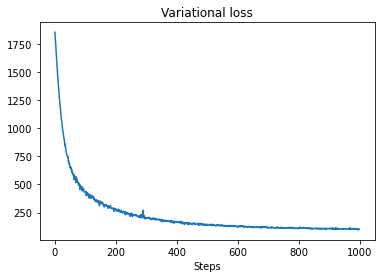
t0 = time.time()
losses = tfp.vi.fit_surrogate_posterior(pinned_model.unnormalized_log_prob,
surrogate_posterior,
optimizer=tf.optimizers.Adam(0.1),
num_steps=num_variational_steps)
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 11.37s.
plt.plot(losses)
plt.title("Variational loss")
_ = plt.xlabel("Steps")
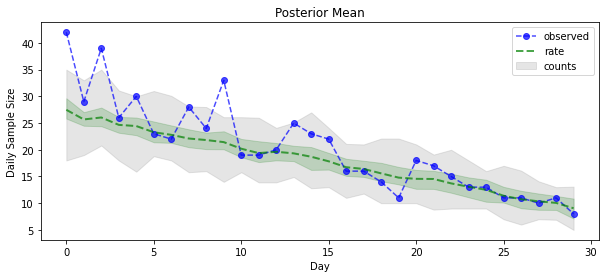
posterior_samples = surrogate_posterior.sample(50)
param_samples = posterior_samples[:-1]
unconstrained_rate_samples = posterior_samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)
plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(
np.random.poisson(rate_samples), [10, 90], axis=0)
_ = plt.plot(observed_counts, color='blue', ls='--', marker='o',
label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color='green',
ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(
np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey',
label='counts', alpha=0.2)
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
plt.title('Posterior Mean')
plt.legend()
<matplotlib.legend.Legend at 0x7f93ff4735c0>
forecast_samples, rate_samples = sample_forecasted_counts(
sts_model,
posterior_latent_rates=unconstrained_rate_samples,
posterior_params=param_samples,
# Days to forecast:
num_steps_forecast=30,
num_sampled_forecasts=100)
forecast_samples = np.squeeze(forecast_samples)
plot_forecast_helper(observed_counts, forecast_samples, CI=80)