استنباط تقریبی مدلهای STS با مشاهدات غیر گاوس

مشاهده در TensorFlow.org

در Google Colab اجرا شود

مشاهده منبع در GitHub

دانلود دفترچه یادداشت

این نوت بوک استفاده از ابزارهای استنتاج تقریبی TFP را برای ترکیب یک مدل مشاهده (غیر گاوسی) هنگام برازش و پیش‌بینی با مدل‌های سری زمانی ساختاری (STS) نشان می‌دهد. در این مثال، ما از یک مدل مشاهده پواسون برای کار با داده های شمارش گسسته استفاده می کنیم.

import time
import matplotlib.pyplot as plt
import numpy as np

import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp

from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd

tf.enable_v2_behavior()

داده های مصنوعی

ابتدا تعدادی داده شمارش مصنوعی تولید می کنیم:

num_timesteps = 30
observed_counts = np.round(3 + np.random.lognormal(np.log(np.linspace(
    num_timesteps, 5, num=num_timesteps)), 0.20, size=num_timesteps)) 
observed_counts = observed_counts.astype(np.float32)
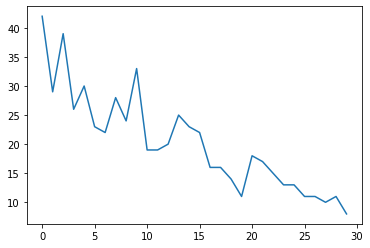
plt.plot(observed_counts)

[<matplotlib.lines.Line2D at 0x7f940ae958d0>]

مدل

ما یک مدل ساده با روند خطی به طور تصادفی مشخص می کنیم:

def build_model(approximate_unconstrained_rates):
  trend = tfp.sts.LocalLinearTrend(
      observed_time_series=approximate_unconstrained_rates)
  return tfp.sts.Sum([trend],
                     observed_time_series=approximate_unconstrained_rates)

این مدل به جای کار بر روی سری‌های زمانی مشاهده‌شده، روی مجموعه‌ای از پارامترهای نرخ پواسون که بر مشاهدات حاکم هستند، عمل می‌کند.

از آنجایی که نرخ پواسون باید مثبت باشد، از یک بیژکتور برای تبدیل مدل STS با ارزش واقعی به توزیعی روی مقادیر مثبت استفاده می کنیم. Softplus تحول \(y = \log(1 + \exp(x))\) یک انتخاب طبیعی است، چرا که آن را تقریبا خطی برای ارزش های مثبت، اما گزینه های دیگر مانند Exp (که تبدیل گام تصادفی نرمال را به یک پیاده روی تصادفی لگ نرمال) نیز امکان پذیر است.

positive_bijector = tfb.Softplus()  # Or tfb.Exp()

# Approximate the unconstrained Poisson rate just to set heuristic priors.
# We could avoid this by passing explicit priors on all model params.
approximate_unconstrained_rates = positive_bijector.inverse(
    tf.convert_to_tensor(observed_counts) + 0.01)
sts_model = build_model(approximate_unconstrained_rates)

برای استفاده از استنتاج تقریبی برای یک مدل مشاهده غیر گاوسی، مدل STS را به عنوان توزیع مشترک TFP رمزگذاری می کنیم. متغیرهای تصادفی در این توزیع مشترک پارامترهای مدل STS، سری زمانی نرخ‌های پواسون نهفته و تعداد مشاهده‌شده هستند.

def sts_with_poisson_likelihood_model():
  # Encode the parameters of the STS model as random variables.
  param_vals = []
  for param in sts_model.parameters:
    param_val = yield param.prior
    param_vals.append(param_val)

  # Use the STS model to encode the log- (or inverse-softplus)
  # rate of a Poisson.
  unconstrained_rate = yield sts_model.make_state_space_model(
      num_timesteps, param_vals)
  rate = positive_bijector.forward(unconstrained_rate[..., 0])
  observed_counts = yield tfd.Poisson(rate, name='observed_counts')

model = tfd.JointDistributionCoroutineAutoBatched(sts_with_poisson_likelihood_model)

آمادگی برای استنباط

ما می خواهیم با توجه به تعداد مشاهده شده، کمیت های مشاهده نشده را در مدل استنتاج کنیم. ابتدا، چگالی ورود به سیستم را بر اساس تعداد مشاهده شده شرط می کنیم.

pinned_model = model.experimental_pin(observed_counts=observed_counts)

همچنین برای اطمینان از اینکه استنتاج به محدودیت‌های پارامترهای مدل STS احترام می‌گذارد (مثلاً مقیاس‌ها باید مثبت باشند) به یک بیژکتور محدود کننده نیاز داریم.

constraining_bijector = pinned_model.experimental_default_event_space_bijector()

استنباط با HMC

ما از HMC (به طور خاص، NUTS) برای نمونه برداری از پارامترهای مدل خلفی مفصل و نرخ های نهفته استفاده می کنیم.

این به طور قابل توجهی کندتر از تطبیق یک مدل استاندارد STS با HMC خواهد بود، زیرا علاوه بر پارامترهای مدل (تعداد نسبتاً کم) ما باید کل سری نرخ‌های پواسون را نیز استنتاج کنیم. بنابراین ما برای تعداد نسبتاً کمی از مراحل اجرا خواهیم کرد. برای کاربردهایی که کیفیت استنتاج حیاتی است، ممکن است افزایش این مقادیر یا اجرای چندین زنجیره منطقی باشد.

پیکربندی نمونه

# Allow external control of sampling to reduce test runtimes.
num_results = 500 # @param { isTemplate: true}
num_results = int(num_results)

num_burnin_steps = 100 # @param { isTemplate: true}
num_burnin_steps = int(num_burnin_steps)

در ابتدا ما یک نمونه مشخص، و سپس با استفاده از sample_chain به اجرای آن هسته نمونه به نمونه تولید.

sampler = tfp.mcmc.TransformedTransitionKernel(
    tfp.mcmc.NoUTurnSampler(
        target_log_prob_fn=pinned_model.unnormalized_log_prob,
        step_size=0.1),
    bijector=constraining_bijector)

adaptive_sampler = tfp.mcmc.DualAveragingStepSizeAdaptation(
    inner_kernel=sampler,
    num_adaptation_steps=int(0.8 * num_burnin_steps),
    target_accept_prob=0.75)

initial_state = constraining_bijector.forward(
    type(pinned_model.event_shape)(
        *(tf.random.normal(part_shape)
          for part_shape in constraining_bijector.inverse_event_shape(
              pinned_model.event_shape))))

# Speed up sampling by tracing with `tf.function`.
@tf.function(autograph=False, jit_compile=True)
def do_sampling():
  return tfp.mcmc.sample_chain(
      kernel=adaptive_sampler,
      current_state=initial_state,
      num_results=num_results,
      num_burnin_steps=num_burnin_steps,
      trace_fn=None)

t0 = time.time()
samples = do_sampling()
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))

Inference ran in 24.83s.

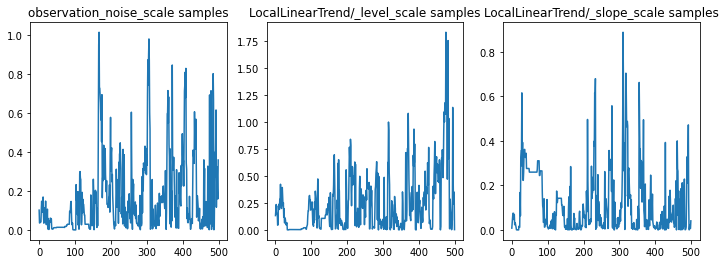
ما می توانیم با بررسی ردیابی پارامترها، استنتاج را بررسی کنیم. در این مورد، به نظر می‌رسد که آن‌ها توضیحات متعددی را برای داده‌ها بررسی کرده‌اند، که خوب است، اگرچه نمونه‌های بیشتر برای قضاوت در مورد میزان اختلاط زنجیره مفید خواهد بود.

f = plt.figure(figsize=(12, 4))
for i, param in enumerate(sts_model.parameters):
  ax = f.add_subplot(1, len(sts_model.parameters), i + 1)
  ax.plot(samples[i])
  ax.set_title("{} samples".format(param.name))

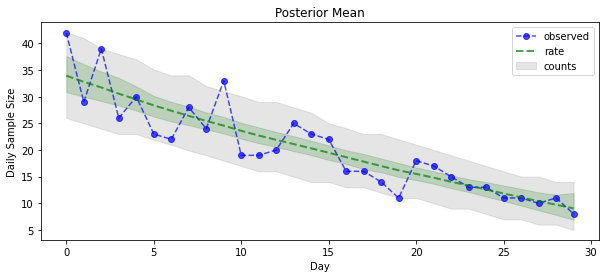
اکنون برای بازده: بیایید نرخ های پسین نسبت به پواسون را ببینیم! ما همچنین فاصله پیش‌بینی‌کننده 80 درصدی را روی تعداد مشاهده‌شده ترسیم می‌کنیم و می‌توانیم بررسی کنیم که به نظر می‌رسد این فاصله شامل حدود 80 درصد از شمارش‌هایی است که ما واقعاً مشاهده کرده‌ایم.

param_samples = samples[:-1]
unconstrained_rate_samples = samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)

plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(np.random.poisson(rate_samples), 
                                       [10, 90], axis=0)

_ = plt.plot(observed_counts, color="blue", ls='--', marker='o', label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color="green", ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey', label='counts', alpha=0.2)
plt.xlabel("Day")
plt.ylabel("Daily Sample Size")
plt.title("Posterior Mean")
plt.legend()

<matplotlib.legend.Legend at 0x7f93ffd35550>

پیش بینی

برای پیش‌بینی تعداد مشاهده‌شده، از ابزار استاندارد STS برای ایجاد توزیع پیش‌بینی بر روی نرخ‌های نهفته استفاده می‌کنیم (در فضای نامحدود، دوباره چون STS برای مدل‌سازی داده‌های با ارزش واقعی طراحی شده است)، سپس پیش‌بینی‌های نمونه‌شده را از طریق مشاهده پواسون منتقل می‌کنیم. مدل:

def sample_forecasted_counts(sts_model, posterior_latent_rates,
                             posterior_params, num_steps_forecast,
                             num_sampled_forecasts):

  # Forecast the future latent unconstrained rates, given the inferred latent
  # unconstrained rates and parameters.
  unconstrained_rates_forecast_dist = tfp.sts.forecast(sts_model,
    observed_time_series=unconstrained_rate_samples,
    parameter_samples=posterior_params,
    num_steps_forecast=num_steps_forecast)

  # Transform the forecast to positive-valued Poisson rates.
  rates_forecast_dist = tfd.TransformedDistribution(
      unconstrained_rates_forecast_dist,
      positive_bijector)

  # Sample from the forecast model following the chain rule:
  # P(counts) = P(counts | latent_rates)P(latent_rates)
  sampled_latent_rates = rates_forecast_dist.sample(num_sampled_forecasts)
  sampled_forecast_counts = tfd.Poisson(rate=sampled_latent_rates).sample()

  return sampled_forecast_counts, sampled_latent_rates

forecast_samples, rate_samples = sample_forecasted_counts(
   sts_model,
   posterior_latent_rates=unconstrained_rate_samples,
   posterior_params=param_samples,
   # Days to forecast:
   num_steps_forecast=30,
   num_sampled_forecasts=100)

forecast_samples = np.squeeze(forecast_samples)

def plot_forecast_helper(data, forecast_samples, CI=90):
  """Plot the observed time series alongside the forecast."""
  plt.figure(figsize=(10, 4))
  forecast_median = np.median(forecast_samples, axis=0)

  num_steps = len(data)
  num_steps_forecast = forecast_median.shape[-1]

  plt.plot(np.arange(num_steps), data, lw=2, color='blue', linestyle='--', marker='o',
           label='Observed Data', alpha=0.7)

  forecast_steps = np.arange(num_steps, num_steps+num_steps_forecast)

  CI_interval = [(100 - CI)/2, 100 - (100 - CI)/2]
  lower, upper = np.percentile(forecast_samples, CI_interval, axis=0)

  plt.plot(forecast_steps, forecast_median, lw=2, ls='--', marker='o', color='orange',
           label=str(CI) + '% Forecast Interval', alpha=0.7)
  plt.fill_between(forecast_steps,
                   lower,
                   upper, color='orange', alpha=0.2)

  plt.xlim([0, num_steps+num_steps_forecast])
  ymin, ymax = min(np.min(forecast_samples), np.min(data)), max(np.max(forecast_samples), np.max(data))
  yrange = ymax-ymin
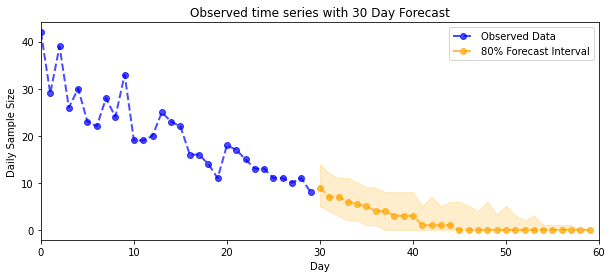
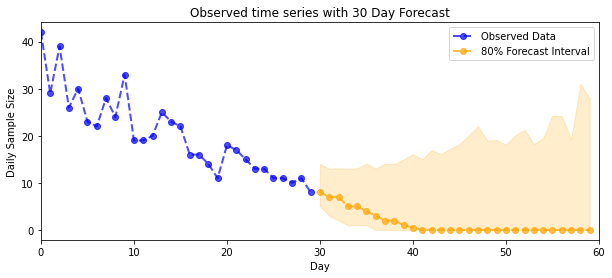
  plt.title("{}".format('Observed time series with ' + str(num_steps_forecast) + ' Day Forecast'))
  plt.xlabel('Day')
  plt.ylabel('Daily Sample Size')
  plt.legend()

plot_forecast_helper(observed_counts, forecast_samples, CI=80)

استنتاج VI

استنتاج تغییرات می تواند مشکل ساز که استنتاج کامل سری های زمانی، مانند تعداد تقریبی ما (به عنوان تنها پارامترهای یک سری زمانی مخالف، به عنوان در مدل های STS استاندارد). این فرض استاندارد که متغیرها دارای پسین مستقل هستند، کاملاً اشتباه است، زیرا هر مرحله زمانی با همسایگان خود مرتبط است، که می تواند منجر به دست کم گرفتن عدم قطعیت شود. به همین دلیل، HMC ممکن است انتخاب بهتری برای استنتاج تقریبی نسبت به سری های تمام وقت باشد. با این حال، VI می‌تواند کمی سریع‌تر باشد و ممکن است برای نمونه‌سازی مدل یا در مواردی که عملکرد آن به‌اندازه کافی خوب نشان داده شود، مفید باشد.

برای تطبیق مدل خود با VI، ما به سادگی یک جانشین خلفی می سازیم و بهینه می کنیم:

surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
    event_shape=pinned_model.event_shape,
    bijector=constraining_bijector)

# Allow external control of optimization to reduce test runtimes.
num_variational_steps = 1000 # @param { isTemplate: true}
num_variational_steps = int(num_variational_steps)

t0 = time.time()
losses = tfp.vi.fit_surrogate_posterior(pinned_model.unnormalized_log_prob,
                                        surrogate_posterior,
                                        optimizer=tf.optimizers.Adam(0.1),
                                        num_steps=num_variational_steps)
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))

Inference ran in 11.37s.

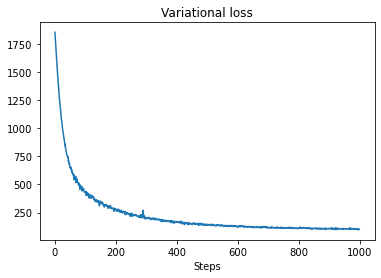
plt.plot(losses)
plt.title("Variational loss")
_ = plt.xlabel("Steps")

posterior_samples = surrogate_posterior.sample(50)
param_samples = posterior_samples[:-1]
unconstrained_rate_samples = posterior_samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)

plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(
    np.random.poisson(rate_samples), [10, 90], axis=0)

_ = plt.plot(observed_counts, color='blue', ls='--', marker='o',
             label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color='green',
             ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(
    np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey',
    label='counts', alpha=0.2)
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
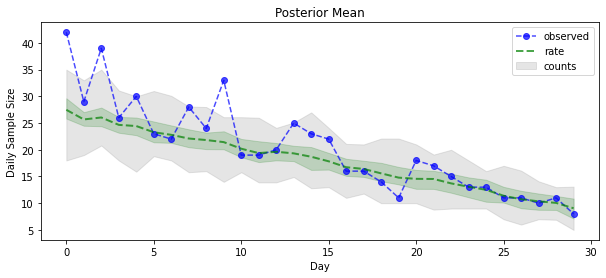
plt.title('Posterior Mean')
plt.legend()

<matplotlib.legend.Legend at 0x7f93ff4735c0>

forecast_samples, rate_samples = sample_forecasted_counts(
   sts_model,
   posterior_latent_rates=unconstrained_rate_samples,
   posterior_params=param_samples,
   # Days to forecast:
   num_steps_forecast=30,
   num_sampled_forecasts=100)

forecast_samples = np.squeeze(forecast_samples)

plot_forecast_helper(observed_counts, forecast_samples, CI=80)